Effect of Porosity on the Laminar Condensation Type Thin Film on a Vertical Wall in Forced Convection ()

1. Introduction
The porous medium is composed of a solid matrix within which is located the pores (typically these pores are interconnected, optionally isolating those not involved in the flow of fluid). The study, presented in this paper, is part of the macroscopic study of heat transfer, and mass flows in the process characterized by the simultaneous presence of a fluid medium and a porous layer. Research in this area covers a very wide field. For applications concerned are extremely varied.
Tong Bou Chang et al. [1] have studied an analytical investigation performed into the problem of steady film wise condensation flow over the outside surface of a horizontal tube embedded in a porous medium with suction at the tube surface. As in classical film condensation problems, an assumption is made that the condensate and vapor layers meet at a common boundary rather than being separated by an intermediary two-phase zone. Furthermore, it is assumed that the condensate film has constant properties and conforms to Darcy’s law within the porous medium. By introducing an effective suction function to represent the effect of the wall suction on the thickness of the liquid film, both the local condensate film thickness and the local Nusselt number are derived using a simple numerical shooting method. The analytical results indicate that the mean Nusselt number depends on the Darcy number, the Jakob number, the Rayleigh number and the suction parameter. Furthermore, it is found that the local Nusselt number has a maximum value at the upper surface of the horizontal tube and reduces toward zero at the lower surface as a result of the finite thickness of the condensate layer.
Zhulev Yu. G et al. [2] examined numerical solutions obtained for the system differential equations describing the process of condensation of a saturated vapor flowing over an isothermal surface.
Nagendra H. R. et al. [3] presented the effect of inclination on laminar film condensation over and under isothermal flat plates which are investigated analytically. The complete set of Navier Stokes equations in two dimensions is considered. Analysed as a perturbation problem, the zero-order perturbation represents the boundary layer equations. First and second-order perturbations are solved to bring about the leading edge effects. Corresponding velocity and temperature profiles are presented. The results show a decrease in heat transfer with larger ||inclinations|| from the vertical. Comparison with experimental data of Gerstmann and Griffith indicates a closer agreement of the present results than the analytical results of the same authors.
Tong Bou Chang et al. [4] have developed a study that investigates the heat transfer characteristics and entropy generation rate of a condensate film formed on a horizontal plate with suction at the wall. Applying the minimum mechanical energy principle, the dimensionless liquid film thickness along the plate is found to vary as a function of the Rayleigh number, the Jakob number, the Prandtl number and the suction parameter. The governing differential equation of the condensate thickness is solved numerically by using a finite-difference shooting method. Closed-form analytical expressions are derived for the Nusselt number and the dimensionless overall entropy generation number. When there is no suction at the wall, the results obtained from the analytical expression for the Nusselt number are found to be in good agreement with those presented in the literature.
Asbik M. et al. [5] presented a problem of forced convection condensation in a thin porous layer is considered. The flow in the porous region is described by the Darcy-Brinkman-Forchheimer model (DBF) while classical boundary layer equations without inertia and enthalpy terms are used in the pure condensate region. In order to resolve this problem, an analytical method is proposed. Then, analytical solutions for the flow velocity, temperature distributions and the local Nusselt number are obtained. The results are essentially presented in the form of the velocity and temperature profiles within the porous layer, the dimensionless film thickness and the heat transfer represented by the local Nusselt number. A comparison of the (DBF) model and the Darcy-Brinkman (DB) one is carried out. The effects of the effective viscosity (Reynolds number ReK), permeability (Darcy number Da) and dimensionless thickness of porous coating H* on the flow and the heat transfer enhancement are also documented.
Hill, A. A. et al. [6] extend their work to the linear and nonlinear stability analyses of vertical through flow in a fluid saturated porous layer, which is modelled using a cubic Forchheimer model, are studied. To ensure unconditional nonlinear results are obtainable, and to avoid the loss of key terms, a weighted functional is used in the energy analysis. The linear instability and nonlinear stability thresholds show considerable agreement when the vertical through flow is small, although there is substantial deterioration of this agreement as the vertical through flow increases.
Avramenko, A. A. et al. [7] have studied instability of a laminar flow in a parallel-plate channel filled with a fluid saturated porous medium is investigated on the basis of a modified Orr-Somerfield equation. This equation takes into account three drag terms: the Darcy term that describes friction between the fluid and the porous matrix, the Forchheimer quadratic drag term that describes a form drag due to the solid obstacles, and the Brinkman term, which is a viscous term similar to the Laplacian term in the Navier-Stokes equations. Numerical analysis is carried out using the collocation method. The dependence of the critical Reynolds number on porosity and permeability of the porous medium is analyzed numerically.
Lage, J. L. et al. [8] present an experimental determination of permeability K and form coefficient C, two hydraulic properties necessary to characterize a porous medium, is beset with undesired secondary effects, which augment the uncertainties in their determination. This study sets forth a new measuring protocol, with derived model equations, to guide the design of experiments for accurate determination of K and C, using Darcy law of flow through a porous medium and Newton law of flow around a bluff body as constitutive equations defining K and C, respectively. The analysis shows that the model equation for measuring C requires the separation between the viscous-drag effect imposed by the porous medium and the viscous effect of the boundary walls on the measured pressure drop when defining K. Furthermore, the model equations suggest large aspect ratio channels and laminar flow with maximum Re as the best choice for measuring K and C (contrary to prevailing belief). The protocol is applicable to either individual or concurrent determination of K and C.
Kim, Y. J. [9] examines the unsteady two-dimensional laminar flow of a viscous incompressible micropolar fluid past a semi-infinite porous plate embedded in a porous medium. The free stream velocity follows an exponentially increasing or decreasing small perturbation law. The porous surface absorbs the micropolar fluid with a time varying suction velocity which has small amplitude. The effects of material parameters on the velocity and temperature fields across the boundary layer are investigated. Numerical results of velocity distribution of micropolar fluids are compared with the corresponding flow problems for a Newtonian fluid. Results show that for the case of a surface cooling by natural convection the skin friction on the porous plate shows an increasing nature up to the critical value of ciscosity ratio. And the surface heat transfer tends to decrease slightly by increasing the magnitude of suction velocity with a given permeablity parameter, and given Prandtl number. However, for a surface heating case, the surface skin friction shows an opposite nature as compared with a surface cooling case.
Mohammed Sammouda et al. [10] studied in their paper the phenomena of double-diffusive convection in a cylindrical enclosure filled with a porous medium saturated with Newtonian fluid. The porosity of the porous media is variable from the walls to the bulk and follows an exponential law. The enclosure is heated from below and two mass concentrations C0, C1 are applied respectively to the surfaces (bottom, top) of the cylinder. The vertical walls are rigid, impermeable and adiabatic. An extended law of Brinkman-Forchheimer (EBFD) describes the fluid flow occurring in the porous layers by using the Boussinesq approximation. The mass concentration follows the basic Fick law, and the model chosen to describe the heat transfer is based on the approximation of one temperature. The heat and mass flow are controlled by the dimensionless numbers such as Rayleigh, Lewis, Darcy, Prandtl number that appear by dimensionless of the system of equations. The finite differences method is used to solve numerically the problem. The study focused on the effect of the dimensionless numbers on the concentrations and the rate of heat transfer profiles in the overall Nusselt number, while considering the porosity uniform or non-uniform. The numerical code developed can be used for various industrial processes involving the phenomenon of natural convection.
We propose in the present work to study numerically the forced convection along a vertical plane wall covered with a homogeneous porous material saturated by a pure liquid by adopting approximations full Darcy-Brinkman model for the porous medium and those of thermal and hydrodynamic boundary layers for the pure liquid.
2. Mathematical Formulation
2.1. Physical Model
This article is devoted to the mathematical modeling that is to say; first, we will give a physical model and simplifying then mathematically formulate the problem and then transform the equations assumptions.
Consider a vertical plate with which is coated by a porous substrate of thickness H, permeability K and porosity ε. The vertical flat plate of length L is positioned in a flow of saturated steam and pure, longitudinal velocity U0. The wall temperature Tw is assumed uniform and lower than the vapor saturation temperature Ts. The film of condensate flows under the influence of gravity and viscous drag forces.
Our field of study includes three (3) areas. The area: 1) is the porous medium saturated with the liquid, the zone 2) corresponds to the liquid film whilst the region 3) is on the saturated vapor. (Figure 1)
2.2. Assumptions
The flow is laminar and two-dimensional and the regime is permanent, the porous matrix is homogeneous and isotropic and is in local equilibrium with the condensate that is in the form of a thin film, the thermo-physical properties of fluids and those of the porous matrix are assumed to be constant. Forces are
![]()
Figure 1. Geometry of the physical model and coordinate system.
negligible viscous dissipation, saturating fluid, the porous medium is Newtonian and incompressible, the dynamic and kinematic viscosity, the actual porous material is equal to those of the film of the condensate, the liquid-vapor interface is in thermodynamic equilibrium and the shear stress is assumed to be negligible. The variation of the transverse pressure is not taken into account.
The Modified wooding model is used to describe the flow in the porous medium, while the classical equations of the boundary layer have been used to describe the transfer in the pure liquid medium, the coupling conditions at the interface porous medium/pure liquid, are essentially expressed by the continuity of the shear stresses and heat flux densities.
We will give the equations of motion, heat in the two media (porous and liquid), the heat balance and mass flow without dimensions are expressed respectively by the following equations:
Porous layer: 
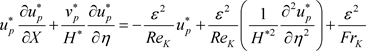 (1)
(1)
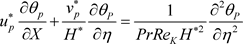 (2)
(2)
Pure liquid: 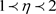
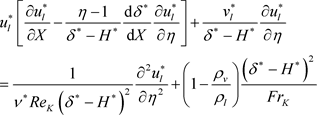 (3)
(3)
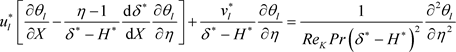 (4)
(4)
The heat balance:
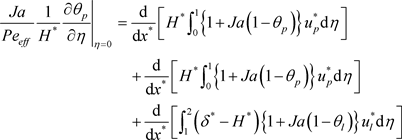 (5)
(5)
The mass flow rate
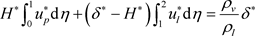 (6)
(6)
2.3. Solution Procedure
The expressions of the partial derivatives involved in the equations are treated deducted from the Taylor expansion.
Since the wall and the boundary of the liquid film, the flow is imposed by the boundary conditions. The equations are discretized transfer by an implicit finite difference method. The mesh of the digital domain is considered uniform in the transverse and longitudinal directions. The terms of advection and diffusion are discretized respectively with a rear and centered upwind scheme. The coupled algebraic equations are solved numerically obtained through an iterative relaxation method line by line Gauss-Seidel.
Thus, the discretization in the field of study of the equations of energy and movement leads to the following algebraic equations:
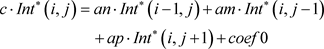 (7)
(7)
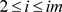 and
and 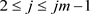
with
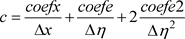 (8)
(8)
 (9)
(9)
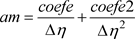 (10)
(10)
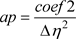 (11)
(11)
Discretization of the equation of heat balance:
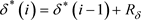 (12)
(12)
Coefficients of the discretization of the equation of heat balance:
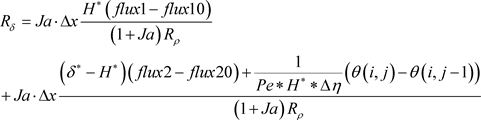 (13)
(13)
![]() (14)
(14)
3. Results and Discussion
The results of our simulations are presented in the figures below.
3.1. Results
Influence of porosity on the adimensionless longitudinal velocity.
The calculations were performed for the following values: λ* = 0.1,
H* = 2 × 10−3, Pr = 2, Ja = 10−3, FrK = 10−4, ReK = 45
Influence of porosity on the adimensionless longitudinal temperature.
The calculations were performed for the following values: λ* = 0.1,
H* = 2 × 10−3, Pr = 2, Ja = 10−3, FrK = 10−4, ReK = 45
Influence of porosity on the adimensionless thickness of the liquid film.
The calculations were performed for the following values: λ* = 0.1,
H* = 2 × 10−3, Pr = 2, Ja = 10−3, FrK = 10−4, ReK = 45
Influence of porosity on the Nusselt number.
The calculations were performed for the following values: λ* = 0.1,
H* = 2 × 10−3, Pr = 2, Ja = 10−3, FrK = 10−4, ReK = 45
3.2. Discussion
The permeability reflects the ease with which the fluid flows into the porous medium under the effect of a pressure gradient. Permeability rated K depends solely on the geometry and porosity of the solid matrix. The relationship Kozeny-Carmen [11], provides an estimate of the permeability K for an unconsolidated porous media consisting of identical elements of simple geometry:
![]() (15)
(15)
or f is a characteristic dimension of the components of the porous matrix and C0 a constant dependent upon the shape of the grains(3.6 < C0 < 5).
Ergun (1988), draws a similar in-Carmen equation Kozney expression whereas unidirectional flow of an incompressible fluid within a column consisting of porous spherical particles of diameter d, and subjected to a gradient of pressure:
![]() (16)
(16)
This corresponds to a value of C0 law Kozney-Carmen.
The porosity is defined as the ratio of the volume occupied by the pores (voids) to the volume of the porous medium.
![]() (17)
(17)
Adimensionless numbers are defined:
![]() (18)
(18)
![]() (19)
(19)
![]() (20)
(20)
![]() (21)
(21)
Nusselt number adimensionless:
![]() (22)
(22)
The equation of motion depends on the porosity ε and the permeability K (see Equation (1)). It also depends on the Reynolds number based on the square root of the permeability of the medium (Equation (19)). The equation of motion of the liquid (Equation (3)) depends implicitly on the porosity, then the latter is linked to the permeability of the medium (Equation (18)). Permeability is related by the equation of motion of the liquid through the Froude number (Equation (18)). The dimensionless longitudinal velocity in both media (porous and liquid) varies substantially with porosity. The medium is therefore not very permeable porous which causes the difficulty of the liquid to flow between the pores of the porous medium (Figure 2).
The equation of the heat in both media (Equation (2) and Equation (4)) depends implicitly on the permeability of the medium via the Reynolds number (Equation (19)) but also speeds. The dimensionless temperature does not vary with porosity. This can be explained by the fact that the variables that bind heat equations of the two media, the permeability of the medium are hydrodynamic quantities (Reynolds number and the adimensionless velocity) (Figure 3).
The Peclet number depends implicitly permeability therefore porosity via the Reynolds number (Equation (20)). The heat balance equation (Equation (5)) the Peclet number depends. Figure 4 shows that the dimensionless thickness of the liquid film does not vary if the porosity ε ≥ 0.2.
If ε < 0.2 there is a variation thereof.
This can be interpreted by the fact that a low value of the porosity allows a better heat exchange between the wall and the vapor phase. This change in thickness causes changes in heat exchange between the wall and the vapor phase. Over the Peclet number, the lower the porosity, the smaller the thickness of the liquid film increases which corresponds to an increase of the heat exchange between the wall and the vapor phase. Indeed over the Peclet number is low (that is to say, the porosity is low), the flow is more slow and thus more condensation is
![]()
Figure 2. Variation of the longitudinal velocity to the ordinate η for different values of ε (porosity).
![]()
Figure 3. Variation of the temperature as a function of longitudinal ordinate η for different values of ε (porosity).
![]()
Figure 4. Variation of the liquid film as a function of the abscissa x for different values of ε (porosity).
![]()
Figure 5. Variation of the Nusselt number depending on the abscissa for different values of x ε (porosity).
promoted. Note that the thickness does not vary for a fixed x-axis as the inverse Peclet number as might suggest the differential equation giving the thickness.
In our problem we calculated the Nusselt number at the interface porous medium/fluid. The Nusselt number is a function of the Reynolds numbers and Prandtl therefore (Nusselt number) depends on the porosity implicitly via the permeability of the medium. The Nusselt number varies in the manner that the dimensionless thickness of the liquid film with respect to porosity. This evolution of the Nusselt number variations causes heat exchange. The higher the porosity, the lower the Nusselt number increases which correspond to an increase of the heat exchange between the liquid medium and the porous (Figure 5).
4. Conclusions
We have in this work mathematically and numerically modeled the transfers of heat and impulse in a porous medium and a liquid phase surmounted by its vapor saturating. Based on simplifying assumptions and the geometry of the domain, the transfer equations are projected onto the coordinate axes. In order to generalize the problem and to weigh the different terms of the equations, we have them adimensionalized thus generating groupings that compare the different effects. The physical domain has a curvilinear boundary, and the use of a homotopic transformation allows us to reduce the study area to a rectangular area in which the top of the boundary layer is identified by a constant coordinate line. To resolve the system of nonlinear and coupled equations, a finite difference scheme implicit is used for its relative ease of implementation. Algebraic equations as well obtained are solved using the double-scan method combined with an iterative scheme of relaxation line by line.
Our study shows that: the temperature does not vary with porosity. Speed in both media (porous and liquid), the Nusselt number and dimensionless liquid film thickness increases slightly with decreasing porosity. From the results obtained, we can conclude that our environment is therefore not very permeable and porous. The non-permeability of the medium results in the difficulty with which the fluid flows into the porous medium, which corresponds to a slight increase in the heat exchange between the wall and the vapor phase, but also between the porous medium and the liquid.
After validating our calculation code by comparing our results with those from the literature and testing the space steps, we analyzed the influences of certain parameters on the hydrodynamic and thermal fields as well as on the parietal sizes. However, this study deserves to be continued and improved by raising, for example, certain simplifying hypotheses, changing geometry, and imposing conditions at more physical thermal limits of the Robin type, for example, by analyzing the effect of the inclination. The influences of the other parameters that we have set must also be analyzed. The study of the influence of the effects of anisotropy in permeability and thermal conductivity and those of the Soret and Dufour effects are also of great interest. Finally, it is important to study this problem in a turbulent regime because in a flow descending, we can consider that the regime is practically turbulent. The results that we would obtain will allow us to better quantify their effects and their importance in thin-film flows.
Nomenclature
Greek Symbols:
![]() : Thickness of the condensate, (m)
: Thickness of the condensate, (m)
![]() : Porosity
: Porosity
![]() : curvilinear coordinate
: curvilinear coordinate
![]() : Temperature dimensionless
: Temperature dimensionless
![]() : Thermal conductivity, (W∙m−1∙K−1)
: Thermal conductivity, (W∙m−1∙K−1)
![]() : Dynamic viscosity, (kg∙m−1∙s−1)
: Dynamic viscosity, (kg∙m−1∙s−1)
![]() : Kinematic viscosity, (m2∙s−1)
: Kinematic viscosity, (m2∙s−1)
![]() : Density, (kg/m3)
: Density, (kg/m3)
(Δx, Δη) respectively represent the step along x and η
Latin Letters:
cp: specific heat, (J∙kg−1∙K−1)
FrK: Froude number based on
i, j: spatial indices relative to X and η directions
g: acceleration of gravity, m∙s−2
H: thickness of the porous layer, (m)
hfg: heat of evaporation, (J∙kg−1)
Ja: Jacob number
K: hydraulic conductivity or permeability, m2
L: length of the plate, m
K: hydraulic conductivity or permeability, m2
Pe: Peclet number
Pr: Prandtl number
Re: Reynolds number based on
T: temperature, (K)
U0: velocity of free fluid (steam), (m/s)
u: velocity along x, (m/s)
ur: velocity reference, (m/s)
v: velocity along y, (m/s)
x, y: cartesian coordinates along x and y, (m)
Indices Exhibitor:
eff: efficiency value
i: porous substrate interface/pure liquid
l: liquid
p: porous
s: saturation
v: steam
w: wall
*: Dimensionless quantity
Nu: Nusselt member