1. Introduction
Let 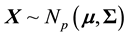 be a normal vector and
be a normal vector and  be a sample taken from this multivariate normal
be a sample taken from this multivariate normal
population. Classical results show that the sample mean vector 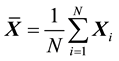 is independent of the sample
is independent of the sample
covariance matrix , where
, where
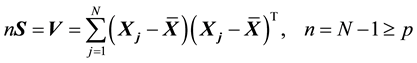 ,
,
and they are distributed respectively, as a normal vector 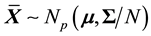 and a central Wishart matrix
and a central Wishart matrix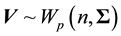 , with
, with 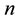 degrees of freedom and covariance matrix
degrees of freedom and covariance matrix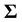 , with density
, with density
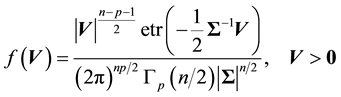 , (1)
, (1)
where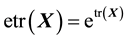 ,
, 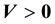 means that
means that 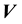 is positive definite matrix, and
is positive definite matrix, and
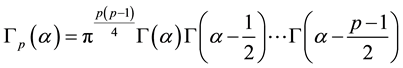 ,
,
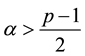 .
.
If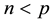 , the distribution is singular and no density exists. The case of pseudo-Wishart matrices will not be considered in detail here.
, the distribution is singular and no density exists. The case of pseudo-Wishart matrices will not be considered in detail here.
Several important results in Multivariate analysis are associated with either the determinant, trace or the eigenvalues of this matrix.
For![]() , we have the non-central Wishart
, we have the non-central Wishart![]() , with non-centrality parameter
, with non-centrality parameter
![]() , which has the more complicated density expression:
, which has the more complicated density expression:
![]() , (2)
, (2)
where![]() , and
, and ![]() is the hypergeometric function with one matrix argument, and reduces to (1) when
is the hypergeometric function with one matrix argument, and reduces to (1) when![]() .
.
We can also have the matrix ![]() formed by the n column vectors
formed by the n column vectors![]() , and consider the product matrix
, and consider the product matrix![]() . We have then
. We have then![]() , where
, where![]() . More general is the case where
. More general is the case where ![]() are independent observations from
are independent observations from![]() ,
, ![]() , with different values for
, with different values for![]() . We then form the
. We then form the ![]() matrix
matrix ![]() and we again have:
and we again have:
![]() , where.
, where.
If we consider at the start the ![]() rectangular matrix as variate, i.e.
rectangular matrix as variate, i.e.![]() ,
, ![]() , the product matrix
, the product matrix ![]() is Wishart, i.e.
is Wishart, i.e.![]() , where
, where![]() , central if
, central if ![]() and
and![]() , or non-central with density (2) otherwise.
, or non-central with density (2) otherwise.
We wish to avoid too technical results in this article, that could digress us from the real purpose of this survey- type article, which is to gather results on the distribution of the trace of the Wishart matrix, that are still scattered in the literature. But several new research results related to this trace, are also presented. In most cases, we will present both the central and the non-central cases, or the null and non-null distributions of a test criterion. It is also natural that we will encounter zonal polynomials, the values of which are not completely known. Finally, due to the extremely complicated mathematical expressions of certain results we will refer the reader to the original publications when this approach appears to be more convenient.
The non-central Wishart distribution has an important role in theoretical Multivariate analysis, but recently has also found some applications, for example in Image Processing [1] .
The Wishart distribution has been generalized in several directions and the most general extension of the Wishart is made by Díaz-García and Guttiérez-Jáimez [2] to which we refer the reader for additional details. Concerning the product of several positive common random univariate random variables, or the ratio of two positive random variates, H-function, or G-function distributions [3] will be used but we will not discuss the best technique to compute the values of these functions by the residue theorem, since this challenging mathematical problem is already an important topic in itself. Maple and Mathematica can deal with fairly complex cases.
In Section 2 we will first recall several special functions that will be used later. In Section 3 we consider the central Wishart distribution and its trace. Similar results are established for the non-central Wishart and its trace in Section 4. Section 5 studies the moments of the trace while Section 6 considers the Wishartness of some quadratic forms. Section 7 considers the sphericity problem where the trace of the Wishart matrix has an important role. Finally, Section 8 considers the latent roots and their ratios to the trace and shows the need of further research in this area. It also proposes the simulation approach that has proven to be very effective in some of our previous works.
2. Some Special Functions
2.1. Special Functions
Table 1 gives all the probability densities treated here.
Advanced statistics make use of several special functions and integral transforms: the Humbert function of the second kind and the Lauricella D-function. They are both defined as infinite series, and extended by analytic continuation and are related to each other. We define:
1) The Lauricella D-function, in ![]() parameters and
parameters and ![]() scalar variables, by:
scalar variables, by:
![]()
where
![]() ,
,
and![]() , which converges for all values of
, which converges for all values of![]() ,
,![]() .
.
2) Similarly, we define the Humbert function, in ![]() parameters and
parameters and ![]() scalar variables, by:
scalar variables, by:
![]()
which converges for all values of![]() .
.
We have the Dirichlet distribution (in n + 1 parameters and n variables), ![]() , with
, with![]() , which also has a key role in multivariate analysis. It has density:
, which also has a key role in multivariate analysis. It has density:
![]() ,
,
where![]() ,
,![]() .
.
The ![]() function in
function in ![]() variables is, in fact, the Laplace transform of the Dirichlet distribution. We have:
variables is, in fact, the Laplace transform of the Dirichlet distribution. We have:
![]() ,
,
where![]() ,
, ![]() and
and![]() .
.
The relation between ![]() and
and ![]() is [4] :
is [4] :
![]() . (3)
. (3)
An extension of ![]() to the matrix variates is given by [5] and an application of
to the matrix variates is given by [5] and an application of ![]() in renewal processes can be found in [6] . On the other hand,
in renewal processes can be found in [6] . On the other hand, ![]() has several integral representations, the most interesting one should be Euler’s type representation, as an hypergeometric integral in one variable:
has several integral representations, the most interesting one should be Euler’s type representation, as an hypergeometric integral in one variable:
![]() , (4)
, (4)
also known as Picard’s integral for![]() .
.
2.2. Integral Representations
Formulas (3) and (4) above allow us to use several interesting mathematical results related to Hypergeometric integrals, which are the focus of much recent work by Gelfand, Krapalov and Zelevinsky [7] , named GKZ integrals. They are also known under the topic of A-Hypergeometric functions [8] during the last thirty years. The various hypergeometric functions in several variables, defined differently according to how variables are summed, and named as Horn, Lauricella, Wright, MacRobert functions etc., can now be integrated into a single approach. The introduction of Grobner basis in their study, by Saito, Sturmfels and Takayama [9] , has lead to other important results.
Since some of the results obtained by our research group are highly mathematical we do not reproduce them here but they can be obtained by writing to the third author.
The trace of a square matrix is defined as the sum of its diagonal elements, and is sometimes used to measure the total variance. So, let![]() , and its univariate density is under study in this article.
, and its univariate density is under study in this article.
For the central Wishart distribution, we will show in the next two sections that when![]() , the trace,
, the trace, ![]() , is a central Chi-square variable.
, is a central Chi-square variable.
3. Central Wishart Distribution
3.1. Two Cases for ![]()
Essentially there are two cases:
1) The matrix sigma is diagonal,![]() : There are several ways to determine the distribution of
: There are several ways to determine the distribution of![]() :
:
Bartlett’s classical decomposition of the Wishart matrix, ![]() , is as follows: Let
, is as follows: Let ![]() where
where ![]() is upper-triangular
is upper-triangular ![]() matrix with positive diagonal elements. Then the elements,
matrix with positive diagonal elements. Then the elements, ![]() ,
, ![]() , are all independent, with the diagonal elements
, are all independent, with the diagonal elements ![]() being
being![]() ,
, ![]() , while the off-diagonal elements
, while the off-diagonal elements ![]() being
being
![]() .
.
Since we have![]() , the diagonal elements will give a chi square with
, the diagonal elements will give a chi square with ![]() degree of freedom, while the off-diagonal give a chi square with
degree of freedom, while the off-diagonal give a chi square with ![]() degree of freedom. Adding them together we then have a chi square with
degree of freedom. Adding them together we then have a chi square with ![]() degree of freedom, i.e.
degree of freedom, i.e.![]() .
.
Another approach: Consists in considering the latent roots on the diagonal matrix ![]() equivalent to
equivalent to![]() ,
, ![]() , with
, with ![]() is orthogonal matrix. These latent roots are
is orthogonal matrix. These latent roots are![]() ,
, ![]() being in-
being in-
dependent, with ![]() being a chi square with
being a chi square with ![]() degree of freedom.
degree of freedom.
REMARK: In the more general case when![]() , then
, then![]() . The trace is then a
. The trace is then a
linear combination of independent central Chi-squares, each with ![]() degree of freedom.
degree of freedom.
PROPOSITION 1. Let![]() ,
, ![]() be the traces of
be the traces of ![]() independent Wishart matrices
independent Wishart matrices![]() .
.
Then we have![]() , with
, with![]() . Furthermore, the product
. Furthermore, the product ![]() and ratios
and ratios![]() ,
, ![]() ,
, ![]() ,
,
can have their densities expressed as G-functions.
PROOF: Immediate from the above results and from [10] , where products and ratios of G-functions are presented.
QED.
2) The matrix sigma is not diagonal,![]() :
:
Results are quite complicated for this case since it involves zonal polynomials, whose expressions are only known for simple cases ([11] , p. 341).
For![]() , the density is a mixture of gamma distributions, and various expressions of it are available in the statistical literature.
, the density is a mixture of gamma distributions, and various expressions of it are available in the statistical literature.
For![]() ,
, ![]() has density
has density
![]() ,
,
where![]() ,
, ![]() and
and ![]() is the zonal polynomial.
is the zonal polynomial.
We have the usual notations: ![]() is arbitrary (chosen to be
is arbitrary (chosen to be![]() ), where
), where ![]() and
and ![]()
are respectively the largest and the smallest latent roots of matrix![]() ,
,![]() is a partition of
is a partition of ![]()
with![]() ,
, ![]() is the zonal polynomial corresponding to
is the zonal polynomial corresponding to![]() ,
, ![]() and
and
![]() .
.
3.2. Other Expressions
Mathai and Pillai (1980) give another expression, quite similar:
![]() .
.
However, using Mellin Transform methods [12] gives the following density function for![]() , which avoids the use of zonal polynomials
, which avoids the use of zonal polynomials
![]() , (5)
, (5)
where![]() , and
, and ![]() is the Humbert hypergeometric function of the second type mentioned earlier.
is the Humbert hypergeometric function of the second type mentioned earlier.
4. Non-Central Wishart Distribution
4.1. The Non-Central Chi-Square Distribution
This distribution is present in many aspects of statistics. Its density is given in our table of densities but below is an alternate expression.
Let ![]() be the modified first Bessel function of the 1st kind
be the modified first Bessel function of the 1st kind
![]() .
.
The associated Bessel density is:
![]() . (6)
. (6)
A particular case of (6) is the non-central Chi-square density with ![]() degrees of freedom and non-centrality parameter
degrees of freedom and non-centrality parameter![]() ,
, ![]() , obtained when
, obtained when
![]() .
.
Its density is then [13] :
![]() , (7)
, (7)
where![]() .
.
Using the above functions Laha [14] proved that the reproductive property of the non-central Chi-square, i.e. the sum of ![]() independent non-central Chi-square is itself a non-central Chi-square, with parameters
independent non-central Chi-square is itself a non-central Chi-square, with parameters ![]() and
and ![]() being the corresponding sums of the related parameters.
being the corresponding sums of the related parameters.
The density of the product or quotient of two non-central chi square variables can be established in closed form using either Fourier transform [14] or Mellin Transform [13] . Following the latter we have:
PROPOSITION 2. Let![]() ,
, ![]() , be two independent non-central Chi-square random variables
, be two independent non-central Chi-square random variables![]() , with densities given by (7). Then the product
, with densities given by (7). Then the product ![]() has as density
has as density
![]() , (8)
, (8)
where ![]() is the modified Bessel function of the third kind and given by
is the modified Bessel function of the third kind and given by
![]() .
.
While the ratio ![]() has as density
has as density
![]() . (9)
. (9)
4.2. The Non-Central Wishart Distribution
As given by (2), its trace ![]() can now be shown to be a non-central Chi-square in some cases.
can now be shown to be a non-central Chi-square in some cases.
First, a simple case is the linear non-central case where the non-centrality parameter is concentrated at one component, can be treated as the central case [15] . For a normal vector![]() , this will happen when only the first component of
, this will happen when only the first component of ![]() is different from 0 and for a normal
is different from 0 and for a normal ![]() matrix
matrix![]() , when only the first line of
, when only the first line of ![]() is different from 0. More precisely, let
is different from 0. More precisely, let
![]() ,
,
where![]() . Then there is a decomposition of
. Then there is a decomposition of![]() , where
, where ![]() is lower triangular with independent elements such that only the first element is a non-central Chi-square, i.e.
is lower triangular with independent elements such that only the first element is a non-central Chi-square, i.e.
![]() ,
,
and![]() ,
,![]() .
.
Hence we have
![]() . (10)
. (10)
The above result on Bessel function distributions now allows us to have the density of sums, product and ratios of the traces of independent linear non-central Wishart distributions. We have the following
THEOREM 1. Let![]() ,
, ![]() with
with ![]() and
and ![]() and
and ![]() be independent, and let
be independent, and let ![]() and
and ![]() be the two respective traces. The sum
be the two respective traces. The sum ![]() is a non-central Chi-square, while for the product
is a non-central Chi-square, while for the product ![]() and ratio
and ratio![]() , their densities can be expressed in closed form, using (8) and (9).
, their densities can be expressed in closed form, using (8) and (9).
PROOF. Applying (10), we have![]() , and similarly for
, and similarly for![]() .
.
For![]() , we have
, we have
![]() .
.
For the product, we have ![]() having density given by (8) for its first component, while for the ratio
having density given by (8) for its first component, while for the ratio![]() , it has density (9) where
, it has density (9) where ![]() and
and![]() , also for its first component. We then use the reproductive property of the non-central Chi-square.
, also for its first component. We then use the reproductive property of the non-central Chi-square.
QED.
4.3. Numerical Example
We can use (8) and (9) to graph the density of the product and quotient of the two traces. Some computer algebra software, Maple and Mathematica, for example, can do the computation in (8) (9) as an infinite series. But the computation, especially for (8), is very slow. Here, we approximate (8) by taking a large number of terms.
![]() ,
,
with the value![]() , this approximation seems to be very good. Let
, this approximation seems to be very good. Let
![]() and,
and,
where ![]() and
and![]() . We get the following graphs of densities of
. We get the following graphs of densities of![]() ,
,
![]() ,
, ![]() and
and![]() , where the horizontal scales are very different (Figure 1).
, where the horizontal scales are very different (Figure 1).
In the case of planar non-centrality, i.e.![]() , as remarked by Anderson [16] , we run into an infinite series of Bessel functions and formulas become very complicated.
, as remarked by Anderson [16] , we run into an infinite series of Bessel functions and formulas become very complicated.
4.4. Case ![]()
We have the following argument, based on the Moment Generating Function (MGF) of ![]() given by [17] :
given by [17] :
For![]() ,
, ![]() , we let
, we let![]() ,
, ![]() , and
, and ![]() , we have
, we have
![]() .
.
Here we set![]() , as in [17] where it is shown that the MGF of
, as in [17] where it is shown that the MGF of ![]() is given by
is given by
![]() ,
,
where ![]() is the j-th diagonal element of
is the j-th diagonal element of![]() ,
, ![]() is the orthogonal matrix such that
is the orthogonal matrix such that
![]() .
.
Using ![]() and, writing
and, writing![]() , we have
, we have
![]() .
.
Using the MGF of the Non-Central Chi-square in our table of densities we have the expression of the trace ![]() in terms of a linear combination of non-central Chi square variables with
in terms of a linear combination of non-central Chi square variables with ![]() degrees of freedom each and non- centrality parameter
degrees of freedom each and non- centrality parameter![]() , the j-th diagonalelement of
, the j-th diagonalelement of![]() , i.e.
, i.e.
![]() , (11)
, (11)
where![]() , with
, with ![]() independent.
independent.
The density of ![]() can be given under a variety of forms by inverting the MGF of
can be given under a variety of forms by inverting the MGF of![]() . [12] , for example, gives 3 forms (see Section 4.7).
. [12] , for example, gives 3 forms (see Section 4.7).
The density of a linear combination of non-central chi-square variables has been the subject of investigation by several authors, since it is associated with quadratic forms in normal variables. Ruben [18] , Press [19] and Hartville [20] seemed to be among the first investigators. More recent is the work of Provost and Ruduik [21] .
The approach using Laguerre expansions seems promising, as shown by some authors, including Castano- Martinez and Lopez-Blasquez [22] . But all the formulas obtained are quite complicated and we refer the readers to these articles. It should be mentioned that using the same MGF, Kourouklis and Moschopoulos [23] give this density as an infinite combination of gamma densities.
4.5. A Simulation Study
Simulation for the density of the trace of non-central Wishart matrix. Following 4.4, let the covariance matrix be
![]() , positive, definite. And the four means be:
, positive, definite. And the four means be:
![]() .
.
With the above means and covariance matrix, we have:
![]() , ,
, ,
![]() , ,
, ,
and the matrix ![]() is computed using:
is computed using:
![]() .
.
![]() .
.
We finally have:![]() ,
, ![]() ,
, ![]() and
and![]() ,
, ![]() ,
,![]() .
.
Now, two approaches are used to obtain the density of![]() :
:
1) Direct approach 1: We use
![]() .
.
We use Matlab command ![]() to generate 4 normal vectors
to generate 4 normal vectors![]() ,
, ![]() , from which we obtain a value of the trace
, from which we obtain a value of the trace![]() . Doing this operation 10,000 times we have the density of
. Doing this operation 10,000 times we have the density of ![]() given by Figure 2.
given by Figure 2.
2) Approach using non-central Chi-squares: We use
![]() ,
,
where![]() ,
, ![]() , and
, and![]() .
.
We use Matlab routine ![]() to generate observations
to generate observations ![]() from
from![]() , and compute
, and compute ![]() 10000 times and we have Figure 3.
10000 times and we have Figure 3.
We can see that the two graphs are very close to each other.
4.6. Modified Traces
The influence of ![]() on
on ![]() is through the coefficients
is through the coefficients![]() . If we remove these coefficients we have the modi-
. If we remove these coefficients we have the modi-
fied trace![]() .
.
PROPOSITION 3: Let![]() ,
, ![]() with non-diagonal
with non-diagonal![]() , be independent and
, be independent and![]() ,
, ![]() be their traces. Let Zi,
be their traces. Let Zi, ![]() be the “modified traces” obtained from Ti by taking
be the “modified traces” obtained from Ti by taking![]() . Then the sum
. Then the sum![]() , and of the product,
, and of the product, ![]() and ratio
and ratio![]() , can be obtained in closed form.
, can be obtained in closed form.
PROOF: Using (11) with ![]() and
and
![]() .
.
Thus, we have
![]() ,
,
and their sum ![]() is itself a non-central Chi- square, with, as parameters the corresponding sums of individual parameters, i.e.
is itself a non-central Chi- square, with, as parameters the corresponding sums of individual parameters, i.e.
![]() .
.
For the product:![]() , we have the same distribution as the product of two non-central Chi-squared random variables, i.e. its density is given by (8). Similarly for the ratio, using (9).
, we have the same distribution as the product of two non-central Chi-squared random variables, i.e. its density is given by (8). Similarly for the ratio, using (9).
QED.
Glueck and Muller [24] also relate the trace of any type of Wishart, singular or nonsingular, central or non- central, true or pseudo, to a weighted sum of non-central Chi-squared random variables and constants. However, the expression of this density is not given, although computational methods are presented, either approximate or permitting to prescribe a degree of accuracy.
4.7. Some Expressions of the Density of ![]()
For some values of the parameters, there can be closed form expression for the density of![]() . For example, [12] gives this density when
. For example, [12] gives this density when ![]() is even (or the sample size
is even (or the sample size ![]() is odd). The formula is however complicated, with reference to other works.
is odd). The formula is however complicated, with reference to other works.
When the general case we have an expression similar to (5), but preceded by the non-central factor:
![]() , (12)
, (12)
with![]() ,
,![]() , and
, and![]() ,
,![]() .
.
where![]() ,
,![]() ,
, ![]() ,
, ![]() ,
,![]() .
.
In terms of zonal polynomials, we have Formula (14) of [12] using common zonal polynomials, or a more compact formula, using Davis expended zonal polynomials![]() .
.
![]() . (13)
. (13)
For ![]() and
and![]() ,
,![]() .
.
5. Moments of the Trace
The trace of ![]() is present in the expressions of several of its moments, and moments are frequently easier to
is present in the expressions of several of its moments, and moments are frequently easier to
obtain than densities themselves. For example, the r-th cumulant of![]() ,
, ![]() , which is the coefficient of
, which is the coefficient of ![]() in
in
the expansion of![]() , where
, where ![]() is the moment generating function of
is the moment generating function of ![]() is found in [17] to be
is found in [17] to be
![]() , which gives the mean of the trace
, which gives the mean of the trace![]() , a result
, a result
also found in [25] . Saw [26] , and Shah and Khatri [27] proved several other results on moments of the trace of the non-central Wishart.
Some results are unexpected. For example, for![]() , and
, and ![]() is a
is a ![]() constant matrix:
constant matrix:
![]() , and using zonal polynomials,
, and using zonal polynomials,
![]() ([15] , p. 98 and p. 106).
([15] , p. 98 and p. 106).
Several other equalities can be found in the same reference.
Letac and Massam [28] , on the other hand, computed the moments of the Wishart matrix![]() , of the form
, of the form![]() , where
, where ![]() is an invariant polynomial in the entries of the matrix
is an invariant polynomial in the entries of the matrix![]() , i.e. depending only on the eigenvalues of
, i.e. depending only on the eigenvalues of![]() . Finally, there are several results available in the literature on the expectation of
. Finally, there are several results available in the literature on the expectation of![]() , which is the sum of all principal minors of order j of matrix
, which is the sum of all principal minors of order j of matrix![]() . For example, for
. For example, for![]() , we have:
, we have:
![]() and,
and,
where![]() .
.
6. The Wishartness of Certain Quadratic Forms
For![]() , it is of interest to look for more general quadratic forms that could also be Wishart.
, it is of interest to look for more general quadratic forms that could also be Wishart.
There are 3 cases of Quadratic forms:
・ ![]() is a unidimensional random variable when
is a unidimensional random variable when![]() . We are interested at
. We are interested at ![]() being a non-central Chi-square variable.
being a non-central Chi-square variable.
・ ![]() is a matrix if
is a matrix if![]() , where
, where![]() . We are interested in the condition for this matrix to be Wishart.
. We are interested in the condition for this matrix to be Wishart.
・ Similarly, ![]() is a random matrix, possibly Wishart when
is a random matrix, possibly Wishart when ![]() is a
is a ![]() normal random matrix.
normal random matrix.
PROPOSITION 4. ([15] , p. 256-257) Let![]() , where
, where![]() . Then the necessary
. Then the necessary
and sufficient condition for ![]() to be distributed as
to be distributed as ![]() is that
is that ![]() is idempotent of rank
is idempotent of rank
![]() . A similar condition applies to
. A similar condition applies to ![]() to be
to be![]() .
.
The trace ![]() of
of ![]() in these cases can be studied as previously. We will not elaborate on this point.
in these cases can be studied as previously. We will not elaborate on this point.
7. Sphericity Testing Criterion
In this section we limit ourselves to the vector case, i.e. of![]() . Understandably, as seen from what precedes, the case
. Understandably, as seen from what precedes, the case ![]() is important, and this test would permit us to accept, or not, that the matrix is diagonal with same diagonal value.
is important, and this test would permit us to accept, or not, that the matrix is diagonal with same diagonal value.
7.1. Sphericity Test
An interesting property of the Gamma distribution in shape parameter ![]() and scale parameter
and scale parameter![]() ,
, ![]() , is that, for a random sample of observations the distribution of the arithmetic mean to the geometric mean is independent of the parameters [29] . An application in telecommunication is given by [30] .
, is that, for a random sample of observations the distribution of the arithmetic mean to the geometric mean is independent of the parameters [29] . An application in telecommunication is given by [30] .
Let ![]() and let
and let ![]() be a sample from this distribution. Let
be a sample from this distribution. Let
![]() .
.
In testing the hypothesis ![]() (or the
(or the ![]() components are equally variable), called sphericity, we can use:
components are equally variable), called sphericity, we can use:
1) The classical likelihood ratio criterion (LRC), ![]() , first used by Mauchly [31]
, first used by Mauchly [31]
![]() . (14)
. (14)
The LRC above is hence the ratio of the geometric mean of the eigenvalues to their arithmetic mean. The null-distribution is the distribution of this criterion under ![]() is the density of the product of betas of the first kind,
is the density of the product of betas of the first kind,
![]() , (15)
, (15)
where![]() ,
,
as shown by [32] . This product can be shown to have a G-function density, namely
![]() , (16)
, (16)
where![]() , and
, and
![]() .
.
2) The product of 2 independent beta products [16] :
![]() ,
,
with ![]() and
and![]() , where
, where ![]() are mutually independent from each other, while
are mutually independent from each other, while ![]() are also mutually independent.
are also mutually independent.
・ ![]() is the test criterion for
is the test criterion for![]() : The matrix is diagonal, and
: The matrix is diagonal, and
・ ![]() is the criterion for
is the criterion for![]() : The diagonal elements are equal.
: The diagonal elements are equal.
Their product is
![]() .
.
Since these two tests are in fact independent the product of the two criteria gives the above sphericity test criterion. [32] has adopted a simulation approach to deal with this product.
7.2. Bartlett’s Test
In univariate statistics, using ![]() different samples to test that the variances of
different samples to test that the variances of ![]() independent normal popula-
independent normal popula-
tions are equal, we have Bartlett’s test for homogeneity, based on![]() , where
, where![]() ,
,
with![]() .
.
When the samples have the same size, Glaser [33] has shown that the null distribution of ![]() is a product
is a product
of independent betas:![]() , where
, where
![]() ,
,
n is sample size and ![]() is shape parameter of the Gamma distribution.
is shape parameter of the Gamma distribution. ![]() is the ratio of the geometric mean to the arithmetic mean.
is the ratio of the geometric mean to the arithmetic mean.
But when these sizes are different [33] shows that the distribution of Bartlett’s statistic, which now is the adjusted ratio of weighted geometric mean of the sample variances to their weighted arithmetic mean, can be obtained with incomplete beta functions.
Gleser ([34] ) considered the two criteria ![]() and
and ![]() above and discussed the interesting relationship between Bartlett’s test and the sphericity test, which become equivalent under a change of variables. In the case of non-normality, Hartley’s test or Levene’s test, can be used to the same purpose.
above and discussed the interesting relationship between Bartlett’s test and the sphericity test, which become equivalent under a change of variables. In the case of non-normality, Hartley’s test or Levene’s test, can be used to the same purpose.
Accepting the hypothesis of sphericity allows us to proceed on to other topics, such as analysis of variance using repeated measures. A generalization of this test to ![]() covariance matrices is possible, and is often known as the Mendoza test.
covariance matrices is possible, and is often known as the Mendoza test.
7.3. Non-Null Distribution
When![]() , we have the non-null distribution of
, we have the non-null distribution of![]() .
.
1) Khatri and Srivastava [35] gives the following expression for the density of the LRC, using both zonal polynomials and Meijer functions:
![]()
where ![]() is the zonal polynomial associated with
is the zonal polynomial associated with![]() .
.
2) [36] propose a convenient strictly numerical method to approximate the power and test size under non- sphericity.
REMARKS. The non-null density in testing diagonality, as given in [37] , is a multiple infinite series involving Meijer functions:
![]() ,
,
where![]() ,
, ![]() is defined in [37] .
is defined in [37] .
Again, here, the computation of the values of this expression is very complicated and we refer the reader to the original paper.
8. Distribution of Ratios of Latent Roots to the Trace
This distribution has attracted renewed interest lately due to its uses in Physics, on random matrices. Krishnaiah and Shurmann [38] were among the first authors to investigate the distributions of these ratios.
The Simulation approach: These distributions have been mentioned by [39] and Johnstone [40] in the context of random matrices. There, the limit theorems are those of Tracy-Widom, or TW, and Wigner. In particular, Nadler reports that, under the hypothesis that![]() , with
, with![]() , than an approximate explicit expression of the distribution of this ratio
, than an approximate explicit expression of the distribution of this ratio![]() , where
, where ![]() is the largest latent root, can be derived, taking into consideration the second derivative of the TW distribution. Computation and simulation methods are used to derive numerical results.
is the largest latent root, can be derived, taking into consideration the second derivative of the TW distribution. Computation and simulation methods are used to derive numerical results.
1) Central case:
a) When the matrix sigma is diagonal:
Let ![]() be the latent roots of the sample covariance matrix
be the latent roots of the sample covariance matrix![]() . The ratio of two latent roots
. The ratio of two latent roots ![]() is also called “condition number” in regression and is associated with collinearity. Troskie [41] gives a very complicated formula based on change of variable technique for the densities of these ratios, which we do not reproduce here. For the ratio of the largest to the trace
is also called “condition number” in regression and is associated with collinearity. Troskie [41] gives a very complicated formula based on change of variable technique for the densities of these ratios, which we do not reproduce here. For the ratio of the largest to the trace![]() , this density is not even tractable. However, [42] gives a relation between the exact null-distribution of the j-th largest root and the distribution of the ratio of this root to the trace, but only for
, this density is not even tractable. However, [42] gives a relation between the exact null-distribution of the j-th largest root and the distribution of the ratio of this root to the trace, but only for![]() .
.
b) When the matrix sigma is not diagonal:
This is even more complex and no result is available on this case. The only resort is by simulation, as in Pham-Gia and Turkkan (2010). Simulation of random matrices, using the appropriate technique, can be very accurate, as shown by several articles by Pham-Gia and Turkkan [39] [43] .
2) Non-central case:
This case is naturally more complicated than the previous one and the simulation approach seems to be the only recourse.
Example
We give below the simulation results related to the ratio![]() . Where
. Where ![]() are latent roots of matrix
are latent roots of matrix ![]() with 10,000 generated observations in cases:
with 10,000 generated observations in cases:
1)![]() ,
, ![]() ,
,![]() .
.
2)![]() ,
, ![]() , and
, and![]() , where
, where![]() ,
,![]() .
.
The simulation results are given by Figure 4 & Figure 5.
9. Conclusions
We have gathered here several important research results related to the trace of a Wishart matrix, and also indicated some potential research topics. Moreover, we have established several connections among these results and proved a few original results. The two main important applications of the trace are the sphericity test and the distribution of the ratio of a latent root to the trace. The lack of results in the second topic clearly shows that research efforts should be made there, as already pointed out by some researchers. Matrix simulation can clearly supply several useful answers.
Finally, as shown in our table of densities, the trace can be further investigated by considering the Gamma random matrix, of which the Wishart is only a special case.
NOTES
*Corresponding author.