Statistical Downscaling of Precipitation and Temperature Using Long Ashton Research Station Weather Generator in Zambia: A Case of Mount Makulu Agriculture Research Station ()
1. Introduction
Global Climate Models (GCMs) from Intergovernmental Panel on Climate Change (IPCC) Third and Fifth Coupled Model Inter-comparison Projects (CMIP3 and CMIP5) are tools used to simulate the current and future climate change (maximum and minimum temperature, precipitation, solar radiation, surface pressure, wind, relative, and specific humidity, geopotential height, etc.) of the earth under different climate change scenarios [1] [2] [3] [4] due to increasing greenhouse gases (GHGs). The GHG emissions scenarios reflect the uncertainty of the future climate and GCMs’ striving to represent complex natural systems [5] . The A1B and B1 represents future scenarios of new, and efficient technologies and ecologically friendly, respectively [5] . The IPCC defines a GCM as a numerical (quantitative) representation of the climate system based on the physical, chemical and biological properties of its components, their interactions and feedback processes [6] , [7] . GCMs play important roles in advancing the scientific understanding of large-scale climate variability and trend [8] . The GCMs focus mostly on changes associated with temperature and precipitation [9] . The GCMs depict the climate using a three-dimensional grid over the globe having a horizontal resolution of, between 250 and 600 km, 10 to 20 vertical layers in the atmosphere and sometimes as many as 30 layers in the oceans [3] . Due to the coarse spatial resolution of GCMs, they cannot be used at local or regional scale for impact studies, hence there is need to bridge the gap between the large scale variables (predictors) and local scale variables (predictands).
The methods used to convert the coarse spatial resolution of GCM outputs into high-spatial resolution of point data [10] are usually referred to as downscaling techniques. There are three available broad approaches to downscaling: 1) dynamics [9] [11] [12] [13] [14] ; 2) statistics [15] [16] ; and 3) hybrid (dynamics-statistics) [17] [18] . All statistical downscaling methods are classified according to three sub-groups [19] [20] namely: 1) Transfer Functions (Regression Models); 2) Synoptic Weather Typing (Weather Classification); and 3) Stochastic Weather Generators [21] . Statistical downscaling technique derives statistical relationships between observed small-scale variables (predictands) and larger (GCM) scale variables (predictors), using either analogue methods, regression analysis or neural network methods [21] [22] . Stochastic weather generators are used in climate change impact studies as computationally inexpensive tool for generating site-specific climate scenarios at a daily time-step with high spatial and temporal resolutions based on GCM outputs [23] [24] [25] .
A stochastic weather generator is a computer algorithm that uses existing meteorological records to produce a long series of synthetic daily weather data of unlimited length for a location based on the statistical characteristics of observed weather data at that location [3] [26] [27] [28] . Stochastic weather generators constitute one of the techniques for developing local scale future climate scenarios from large-scale climate changes simulated by GCMs [29] . It should be understood that stochastic weather generators are not predictive tools, which can be used in weather forecasting, but are a means of generating time-series of synthetic weather that is statistically “identical” to the observed historical weather data [26] . The generated synthetic daily weather data may be used in crop simulation modelling or replace the long-term series of historical data, especially if some data sets are missing or contain erroneous data [30] . In recent years, synthetic weather data generated by weather generators have been used extensively in climate change and variability studies to determine the potential impact on agricultural or hydrological applications [31] [32] [33] [34] .
Agricultural productivity is sensitive to direct and indirect effects from changes in temperature, GHG concentration, and precipitation and in soil moisture and the distribution and frequency of infestation by pests and diseases, respectively. Predicted climate change scenarios may affect crop yield, growth rates, photosynthesis and transpiration rates, soil moisture availability, through changes of water use and agricultural inputs such as herbicides, pesticides, insecticides and fertilizers [35] [36] . [36] reported that the anticipated potential agricultural impacts of the simulated climate change include extreme weather condition (drought and floods), soil water management and soil moisture regime. To this end, there is need for farmers to adopt water use efficiency technologies that reduces surface evaporation, surface runoff, and increases water storage capacity of the soil.
Stochastic weather generators are conventionally developed in two steps [3] [27] : 1) the first step is to model daily precipitation; and 2) the second step is to model the remaining variables of interest such as daily temperature, solar radiation, humidity and wind speed conditional on precipitation occurrence. Different model parameters are usually required for each month to reflect seasonal variations both in the values of the variables themselves and in their cross-cor- relations. Stochastic downscaling approaches involve modifying the parameters of conventional weather generator such as Weather Generator (WGEN) and Long Ashton Research Station Weather Generator (LARS-WG). Of the available statistical downscaling techniques, LARS-WG is preferred as it can be used for the simulation of weather data at a single site [33] based on as little as a single year of historical data [26] [32] [37] [38] under both current and future climate conditions. The data is in the form of daily time-series for precipitation, temperature and solar radiation variables. A recent study showed that LARS-WG performs well and has been well validated in diverse climates around the world [32] [39] . The current LARS-WG version 5.5 includes fifteen (15) GCMs outputs used in CMIP3 IPCC emission scenarios SRA1B, SRA2 and SRB1 which can be used in an ensemble to cope with the GCMs uncertainties.
The LARS-WG version 5.5 also improves simulation of extreme weather events, such as extreme daily precipitation, long dry spells and heat waves [40] [41] . Future climate scenarios incorporate changes in climatic variability as well as changes in mean climate [42] . LARS-WG has not been parameterized and tested in Zambia to be used in generating current and future climate scenarios from GCMs outputs for impact studies. Reliable data and analysis of temperature and precipitation evolution is an important aspect in generating current and future climate scenarios. If a weather generator is adequately calibrated and validated in simulating the mean as well as extreme properties of temperature and precipitation (wet/dry spell length and annual maximum rainfall) it can be adopted as a simplified, computationally inexpensive local solution for incorporating climate change information into decision support systems [41] . The objectives of this study were: to assess the suitability of LARS-WG in predicting climate change for 2020s and 2055s according to the projections of HadCM3 and BCCR-BCM2 GCMs for B1 and A1B scenarios.
2. Materials and Methods
2.1. Study Site
The study site was Mount Makulu Research Station in Chilanga (Latitude: 15.550˚S, Longitude: 28.250˚E, Elevation: 1213 meter). The Region receives between 800 to 1000 mm of annual rainfall. The climate at the site is described as a wet and dry tropical and sub-tropical and is modified by altitude [43] .
2.2. Weather Data
Historical climate data for daily rainfall (precip), minimum (Tmin) and maximum (Tmax) air temperature was obtained from the Zambia Meteorological Department (ZMD) for the period 1981-2010 and the Agricultural Modern-Era Retrospective Analysis for Research and Applications (AgMERRA) Climate Forcing Dataset for Agricultural Modeling for the period 1981-2010 [44] (Figure 1). The weather data from ZMD data did not include solar radiation. 5.39%, 4.39% and 1.95% of the Tmin, Tmax and precipitation data was missing from the observed station data. On the other hand, the AgMERRA datasets are stored at 0.25˚ × 0.25˚ horizontal resolution (~25 km), with global coverage and daily
![]()
Figure 1. Observed station and AgMERRA reanalysis data for precipitation and temperature.
values from 1980-2010 in order to form a “baseline or current period” climato- logy [44] . The AgMERRA reanalysis data was collected from AgMERRA Climate Forcing Dataset for Agricultural Modeling (https://data.giss.nasa.gov/impacts/agmipcf/agmerra/).
2.3. General Circulation Models
The Hadley Centre Couple Model version 3 (HadCM3) and Bergen Climate Model Version 2 (BCCR-BCM2) models were used in the IPCC Third and Fourth Assessments and also contributed to the Fifth Assessment Reports [45] . These two models differ in spatial resolution power, design institute, predictability of atmospheric variables, and predictability of oceanic variables [46] [47] . The oceanic component of HadCM3 has a horizontal resolution of 1.25˚ × 1.25˚ and comprises 20 levels. The HadCM3 GCM is ranked highly (fourth out of 22 CMIP3 models) when compared with other GCMs. The simulation of HadCM3 assumes the year length in 360 day calendar with 30 days per month [48] . The model was developed in 1999 and was the first coupled atmosphere-ocean which did not require flux adjustments [49] . It also has the capability to capture the time-dependent fingerprint of historical climate change in response to natural and anthropogenic forcings [45] and this has made it an important tool in studies concerning the detection and attribution of past climate changes.
The Bergen Climate Model Version 2 (BCCR-BCM2) is a fully-coupled atmosphere-ocean-sea-ice model that provides state-of-the-art computer simulations of the present and future climate scenarios [50] . It is deployed at Bjerknes Centre for Climate Research (Norway) Computer. The model has oceanic resolution [1.5˚ × 1.5˚ (0.5˚) L35] of 35 vertical layers and approximately square horizontal grid cells with 1.5˚ grid spacing along the equator [51] [52] . Near the equator the meridional grid spacing is gradually decreased to 0.5˚. It has a triangular truncation T63 with “linear” reduced Gaussian grid equivalent to T42 quadratic grid (2.8˚) [53] .
2.4. Description of LARS-WG Stochastic Weather Generator Model
The Long Ashton Research Station Weather Generator (LARS-WG) is a stochastic weather generator [38] used for the simulation of weather data at a single site [33] , under both current and future climate conditions. The data required by the weather generator is in the form of daily time-series for precipitation (mm), maximum and minimum temperature (˚C) and solar radiation (MJ·m−2·day−1) variables. LARS-WG accepts sunshine hours as an alternative to solar radiation data. If solar radiation data are unavailable, then sunshine hours are used to estimate solar radiation using the approach described in [54] .
LARS-WG as a stochastic weather generator utilizes a semi empirical distribution (SED) which is specified as the cumulative probability distribution function (CPDF) [55] to approximate probability distribution of dry and wet series of daily precipitation, minimum, and maximum temperature and daily solar radiation [33] [48] . The number of intervals (n) used in SED is 23 for climate variable [48] compared with ten (10) used in the previous versions. LARS-WG simulates time-series of daily weather data at a single site “statistically” identical to the observed data and can be used to: 1) generate long-term time-series weather data suitable for risk assessment in agricultural and hydrological studies; 2) provide the means of extending the simulation of weather data to unobserved locations; and 3) serve as a computationally inexpensive tool to produce daily site-specific climate change scenarios based on outputs from general (global) and regional climate models for impact assessments of climate change. LARS-WG produces synthetic daily time series of maximum and minimum temperature, precipitation and solar radiation [56] .
2.5. Weather Generation Process and Testing Performance
The process of generating local-scale daily climate scenario data in LARS-WG is divided into two steps of analysis and generator and briefly described by [33] and [57] (Figure 2). The baseline data [observed station data (1981-2010) and AgMERRA reanalysis (1981-2010)] were used to perform site analysis and generation of synthetic time series data using LARS-WG for HadCM3 and BCCR- BCM2 GCMs under B1 and A1B scenarios.
Analysis (site analysis and model calibration): Observed daily and AgMERRA reanalysis weather data for the site were analyzed to compute site parameters and these were stored in two files: a wgx-file (site parameters file) and a stx-file (additional statistics), respectively.
Generator (generation of synthetic weather data or site scenarios): the site parameter files derived from observed daily weather data was used to generate synthetic daily time series which statistically resembles the observed weather. The synthetic data corresponding to a particular climate change scenario may also be generated by applying global climate model-derived changes in precipitation, temperature and solar radiation to the LARS-WG parameter file [33] [57] . Statistical tests used in this study included the Kolmogorov-Simirnov (K-S) test
![]()
Figure 2. Systematic structure of downscaling weather data in LARS-WG.
to compare the probability distributions, T-test to compare means and F-test to compare standard deviations. The statistical tests used in LARS-WG v5.5 are based on the assumption that the observed/AgMERRA and synthetic weather data are both random samples from existing distributions and they test the null hypothesis that the two distributions are the same. The LARS-WG was validated by comparing statistics computed from a synthetic weather series generated by the weather generator against those from observed time series weather data [58] .
The annual means of precipitation and temperature were computed using ensembles under SRA1B and SRB1 scenarios. If the calculated mean annual temperature and precipitation amounts (mm year-1) were within the 95% confidence interval (CI95) for the synthetic data, it was concluded that the statistic were simulated accurately for Mt. Makulu.
2.5.1. Generation of Climate Scenarios with LARS-WG
Use of at least 20 - 35 years of daily observed weather data is recommended to determine robust statistical parameters [33] [59] [60] . On the other hand, to model low frequency, high magnitude events, it is desirable to obtain the longest possible observed time series [34] [61] . A long record of observations could possibly contain the full variability of the observed climate and hence allow the downscaling models to better model climate changes [34] . LARS-WG version 5.5 used in this study incorporates climate scenarios based on 15 GCMs used in IPCC 4th Assessment Report (2007) to better deal with uncertainties of GCMs and in this study two GCMs were used. This version of LARS-WG also improves simulation of extreme weather events such as extreme daily precipitation, duration of wet/dry spells and heat waves [57] . The extreme properties of rainfall were analyzed in LARS-WG using baseline data (1981-2010 and 1981-2010) for Mount Makulu.
The calibrated LARS-WG stochastic weather generator was used to generate 30 years of synthetic daily precipitation, minimum and maximum temperature for Mount Makulu for the time slice 2011-2030 [near future (2020)] and 2046- 2065 [medium future (2055)] based on the SRB1 and SRA1B from HadCM3 and BCR2 GCMs for the study site (see Table 1). In LARS-WG model, the GCMs variables are not directly applied, but the model apply the proportionally local station climate variables, which are adjusted to the present climate change [62] .
2.5.2. Modeling Precipitation Occurrence
According to [57] [63] the simulation of precipitation occurrence is modelled as alternate wet and dry series, where a wet day is defined to be a day with precipitation > 0.0 mm. The length of each series is chosen randomly from the wet or dry semi-empirical distribution for the month in which the series starts. In determining the distributions, observed series are also allocated to the month in which they start. For a wet day, the precipitation value is generated from the semi-empirical precipitation distribution for the particular month independent of the length of the wet series or the amount of precipitation on previous days. For each climatic variable v, a value of a climatic variable vi corresponding to the probability pi is calculated [16] [57] as in Equation (1):
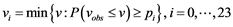 (1)
(1)
![]()
Table 1. CO2 concentrations (ppm) for selected climate scenarios specified in the Special Report on Emissions Scenarios (SRES) [46] [68] .
Note: CO2 concentration for the baseline scenario, 1960-1990, is 334 ppm.
where P() denotes probability based on observed data {vobs}. For each climatic variable, two values, p0 and pn, are fixed as p0 = 0 and pn = 1, with corresponding values of v0 = min{vobs} and vn = max{vobs}. To approximate the extreme values of a climatic variable accurately, some pi are assigned close to 0 for extremely low values of the variable and close to 1 for extremely high values and the remaining values of pi are distributed evenly on the probability scale. Because the probability of very low daily precipitation (<1 mm) is typically relatively high and such low precipitation has very little effect on the output of a process-based impact model, two values of v1 = 0.5 mm and v2 = 1 mm to approximate precipitation within the interval (0,1) with the corresponding probabilities calculated as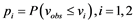 . To account for extremely long dry and wet series, two values close to 1 are used in SEDs for wet and dry series, pn-1 = 0.99 and pn-2 = 0.98 [63] .
. To account for extremely long dry and wet series, two values close to 1 are used in SEDs for wet and dry series, pn-1 = 0.99 and pn-2 = 0.98 [63] .
2.5.3. Modeling Temperature
In LARS-WG v5.5, the maximum and minimum temperatures for dry and wet days are approximated by SEDs calculated for each month, with auto-and-cross- correlations calculated monthly. SEDs for climatic variables are calculated on a monthly basis by LARS-WG while some of the variables follow an annual cycle [63] . To reproduce a smooth seasonal cycle of daily minimum or maximum temperature and daily radiation, the SED is computed for a given day by interpolating between two monthly SEDs. The resulting distribution for each month is a weighted sum of the distributions of the current and the previous or next month. In perturbing maximum and minimum temperatures, two values close to 0 and two values close to 1 are used to account for extremely low and high temperatures, i.e., p2 = 0.01, p3 = 0.02, pn-1 = 0.99 and pn-2 = 0.98. In the LARS-WG v5.5, simulation of the maximum and minimum temperatures for dry and wet days are approximated by SEDs calculated for each month [57] .
2.6. Coefficient of Determination
The coefficient of determination of a linear regression model is the quotient of the variances of the generated (Gen) and observed (Obs) values. The coefficient of determination is computed according to the Equation (2) below:
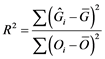 (2)
(2)
where 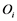 is denoted as the observed values,
is denoted as the observed values, 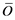 and
and 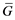 ¯y as its mean, and
¯y as its mean, and 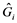 as the generated value.
as the generated value.
2.7. Joint Probability Density Function (JPDF)
Estimating the distribution of random variables is an essential concern to statistics and its related disciplines as stated by [64] . Joint Probability Density Function (JPDF) provides approaches to specifying the probability law that governs the behavior of the pair (X, Y). A joint distribution of two random variables has a probability density function f(x, y) that is a function of two variables (sometimes denoted fx,y(x, y)). The joint behavior of X and Y is fully captured in the joint probability distribution. If X and Y are continuous random variables, then f(x, y) must satisfy the equation below:
1)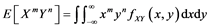 (3)
(3)
or
2)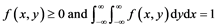 (4)
(4)
If X and Y are discrete random variables, then f(x, y) must satisfy the equations below:
1)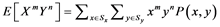 (5)
(5)
or
2)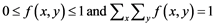 (6)
(6)
The Joint PDF Estimator developed by [64] was used to compute the JPDF for the observed and AgMERRA data. The application was written in Java and reads CSV files. The application estimates JPDFs from sample data, by transforming a set of random variables into a set of independent ones and by computing the marginal PDFs of the latter [64] .
3. Results and Discussion
3.1. Calibration and Validation LARS-WG Results
The Calibration and validation was carried out using the “Site Analysis” and “Qtest” function in LARS-WG model using two data sets, Observed station and AgMERRA reanalysis data, respectively. Performance of the weather generator during the calibration and the validation was checked using Kolmogorov-Simirnov (K-S) test, T-test and the F-test. The performance was also checked by using coefficient of correlation (R) and coefficient of determinant (R2). Evaluating the suitability of LARS-WG performance in simulating precipitation for Mount Makulu is presented in Table 2 and Table 3. It can be observed from the K-S-test that the model performed very well in fitting the DJF (wet/dry), MAM (wet/dry), JJA (wet) and SON (dry) seasons for the two datasets. [63] and [65] reported that LARS-WG was more capable in simulating the seasonal distributions of the wet/dry spells and the daily precipitation distributions in each month. The model performed poorly in fitting the JJA (dry) season. The reason for the poor performance is attributed to lack of precipitation recorded in JJA (dry). Table 4 and Table 5 present the KS-test for daily rain distribution. The assessment results show that LARS-WG performance in simulating daily rainfall distributions for the JFMAOND was perfect except for the months of MJJAS (Observed) and MJJAS (AgMERRA reanalysis). The poor performance was due
![]()
Table 2. K-S-test for seasonal wet/dry SERIES distribution for AgMERRA data.
![]()
Table 3. K-S-test for seasonal wet/dry SERIES distribution for observed data.
![]()
Table 4. KS-test for daily RAIN distributions for AgMERRA data.
![]()
Table 5. KS-test for daily RAIN distributions for station observed data.
ND: Not determined.
to lack of precipitation during the period. The simulation of both minimum and maximum temperature for both data sets was perfect as presented in Tables 6-9. According to [65] weather generators generate synthetic weather time series which have statistical properties similar to the observed time series.
3.2. KS-Test for Seasonal Frost and Heat Spells Distributions: Effective N, KS Statistic and p-Value at Mount Makulu
The seasonal frost and heat spells distributions and the statistical values are presented in Table 10. According to Table 10, Mount Makulu did not experience any seasonal frost. The site experienced heat stress during DJF, MAM, JJA and SON with probabilities of 0.0110, 0.0786, 0.2522, and 0.9995 for AgMERRA reanalysis and 0.7833, 0.0010, 0.0596 and 0.9761 for Observed, respectively at p < 0.05. The results indicate that there was a much higher heat spell events during DJF and SON at Mount Makulu.
3.3. Monthly Means and Standard Deviations for Precipitation, Maximum and Minimum Temperature
Comparison between the monthly mean and standard deviation of precipitation and temperature for the two data sets used in the analysis are presented in Figure 3 and Figure 4. The results showed very good performance of LARS-WG in fitting the monthly means of precipitation, Tmax and Tmin statistics. The mean monthly totals of precipitation, minimum and maximum temperature were well modeled by LARS-WG. This shows that precipitation and temperature could be calculated from daily time series. In a similar study where LARS-WG was used, [32] was able to reproduced the monthly means of maximum and minimum
![]()
Figure 3. Monthly mean observed verses precipitation, maximum and minimum temperature (AgMERRA reanalysis and observed station data).
![]()
Figure 4. Obs versus Gen precipitation sd, tmax sd and tmin sd (AgMERRA reanalysis and observed station data).
![]()
Table 6. KS-test for daily Tmin distributions for AgMERRA data.
![]()
Table 7. KS-test for daily Tmax distributions for AgMERRA data.
![]()
Table 8. KS-test for daily Tmin distributions for station observed data.
![]()
Table 9. KS-test for daily Tmax distributions for station observed data.
![]()
Table 10. KS-test for seasonal frost and heat spells distributions at Mount Makulu.
temperature accurately. Results from statistical tests indicate that there is no significant difference in monthly means of the simulated monthly precipitation compared to the observations. Researchers such as [62] and [63] indicated that downscaling of precipitation was more complex and difficult to obtain a good agreement between observed and generated values compared to downscaling of temperature. This was due to the conditional process which depended on intermediate processes within the rainfall process such as an occurrence of humidity, cloud cover, and/or wet-days. One of the challenges weather generators face was how well to simulate interannual variability [65] . The monthly means of precipitation and minimum and maximum temperature values were generated accurately by LARS-WG giving correlation coefficients and coefficient of determinants equal to unit, respectively (see Figure 3). The R2 for the mean monthly precipitation, minimum, and maximum temperature had a strong linear relationship between observed/AgMERRA and synthetic data as presented in Figure 3.
In terms of standard deviation, LARS-WG showed an excellent performance for precipitation for all the month except February (over-estimated the standard deviation) and November (under-estimated the standard deviation). [65] observed that the means and variances of daily synthetic weather data are supposed to be non-significantly different from those calculated from observed time series. It is also important that synthetic weather series follow a probability distribution which is not statistically different from the observed time series. The temperature monthly standard deviations of the generated values were under estimated for both data sets (Observed station and AgMERRA reanalysis data). [32] and [39] reported similar results. This is the main shortcoming found when LARS- WG was tested for 18 sites worldwide was that the generated (synthetic) data tend to have a lower standard deviation of monthly means than the observed data. The means and standard deviation of the normal vary daily and these parameters are obtained by fitting Fourier series to the means and standard deviations of the observed data throughout the year (grouped into months) [32] . Furthermore, [32] reported that daily minimum and maximum temperatures are considered as stochastic processes were daily means and daily standard deviations are conditioned on the wet or dry status of the day. It was highlighted by [32] that LARS-WG should be evaluated to ensure that the data that it produces is satisfactory for the purposes for which its output is to be used. The required accuracy depends on the application of the generated current and future scenarios and its performance would vary considerably under diverse climatic conditions.
3.4. Future Scenarios of Precipitation, Minimum and Maximum Temperature
The HadCM3 and BCCR-BCM2 GCMs and B1 and A1B scenarios in LARS-WG version 5.5 were used in this study to generate future climate scenarios to better deal with uncertainties. Results for the observed station (1981-2010) and AgMERRA reanalysis (1981-2010) data indicated that the baseline had total annual precipitation of 841.2 mm/year in 64.5 days and total precipitation of 748.1 mm/year in 81.5 days, respectively. The difference in number of days and precipitation amounts is due to missing data in the observed station data. Computed mean ensemble outputs for SRB1 and SRA1B indicates that in 2020 and 2055 the number of days with precipitation would increase by 0.5 - 1.5 and 4 - 4.5 days under the observed station and reanalysis data, respectively. The outputs from observed station data indicated that number of days with precipitation and the amount of precipitation per year would reduce relative to the baseline. The mean amounts of precipitation would increase by 1.67%, 0.31% under SRB1 (2020), SRB1 (2055), respectively. Under the AgMERRA reanalysis data, results showed an increase in the mean amount of precipitation by 5.28%, 3.28%, 4.9% and 1.78% under SRA1B (2020), SRB1 (2020), SRA1B (2055) and SRB1 (2055), respectively. In future Mount Makulu would experience longer annual rainfall days and this finding is not in agreement as reported by [66] . Furthermore, [67] projected that rainfall change over sub-Saharan Africa in the mid and late 21st century would be uncertain.
The mean temperature in 2020 and 2055 would be 21.94˚C and 23.18˚C under SRA1B (Observed station data) and 21.90˚C and 22.83˚C under SRB1 (Observed station data). The temperatures would increase by 0.28˚C - 0.75˚C (2020) and 1.25˚C - 1.71˚C (2050) under SRB1, respectively. The changes in temperature are 0.40˚C - 0.83˚C (SRA1B: 2020), 1.65˚C - 2.08˚C (SRB1: 2055), under scenarios generated using observed station data. The changes in temperature under scenarios generated using AgMERRA reanalysis data would be 0.41˚C - 0.86˚C (SRB1: 2020) and 1.37˚C - 1.81˚C (SRB1: 2055) while the changes in temperature under SRA1B would be 0.47˚C - 0.92˚C (SRA1B: 2020) and 1.73˚C - 2.17˚C (SRA1B: 2055), respectively. The simulated changes in temperature at Mt. Makulu are within the predicted value by IPCC under B1 (1.1˚C - 2.9˚C) and A1B (1.4˚C - 6.4˚C). The observed station data (baseline) (1981-2010) mean temperature is 21.33˚C while the mean temperature for future scenarios are 21.90˚C, 21.94˚C, 22.83˚C, and 23.15˚C under SRB1 (2020), SRA1B (2020), SRB1 (2055) and SRA1B (2055), respectively. On the other hand, the AgMERRA data (1981-2010) mean temperature is 22.21˚C while the mean temperature for future scenarios are 22.75˚C, 22.80˚C, 23.69˚C, and 24.05˚C under SRB1 (2020), SRA1B (2020), SRB1 (2055) and SRA1B (2055), respectively. The results indicate an increasing trend in the mean temperature for Mt. Makulu. The projected temperature changes under A1B and B1 for Mt. Makulu are within the threshold projected by IPCC [1.4˚C - 6.4˚C (A1B) and 1.1˚C - 2.9˚C (B1)] [46] [68] . The SRA1B scenario shows the largest temperature uncertainty in all time slices compared to SRB1.
The ensemble of the HadCM3 and BCM2 GCMs indicated that climate signal for precipitation amount in 2020 and 2055 would increase under observed station data (SRB1) and under AgMERRA reanalysis data (SRB1 and SRA1B). According to the National Climate Assessment [69] multi-member ensembles and model inter-comparison projects (MIP) are used to assess uncertainties in future climate and climate impacts. Uncertainty in GCM outputs determines the range of possible generated future scenarios (see Table 11). The multi-ensembles approach using different climate models and emissions scenarios enables a move towards a more complete assessment of uncertainty in future climate projections [70] [71] .
The CI95 of the future climate scenarios for precipitation and temperature were computed for the two data sets. The CI95 shows values at the upper and lower end. The CI95 and time series for precipitation and temperature are presented in Table 11 and Figure 5, and Figure 6, respectively. [32] indicated that it was vital for the synthetic data to be similar to the observed data on average and the distribution of the whole data set to be similar across their whole range. It is worth mentioning that the means of synthetic future precipitation computed under both scenarios (SRA1B and SRB1) lay within the CI95 of means of the minima and maxima for observed/AgMERRA data. On the other hand, the means of synthetic annual temperature under 2020s (SRA1B, SRB1) and 2055s (SRA1B, SRB1) scenarios lay outside the CI95 of the baseline.
![]()
Table 11. Confidence interval for precipitation and temperature for the observed and agmerra baseline and future scenarios (SRA1B and SRB1).
![]()
Figure 5. Baseline and future annual time series of temperature.
![]()
Figure 6. Baseline and future annual time series of precipitation.
3.5. Joint Probability Distribution Density Function (JPDF)
The Joint Probability Distribution Functions (JPDFs) were estimated for precipitation and temperature using the observed station and AgMERRA reanalysis data. The JPDFs and Joint Cumulative Distribution Functions (JCDFs) for precipitation and temperature for the observed and AgMERRA reanalysis data are presented in Table 12. The overall fitness for observed precipitation, minimum, and maximum temperature were 0.92, 0.96 and 0.81, respectively. On the other hand, the overall fitness for AgMERRA reanalysis precipitation, minimum, and
![]()
Table 12. Joint and cumulative probability distribution functions.
maximum temperature were 0.76, 0.77 and 0.80, respectively. The LARS-WG semi-empirical distribution models precipitation and temperature as a step function and therefore its shape only approximately follows the shape of the observed/AgMERRA values. The shape of the distribution for observed and AgMERRA data approximately follows that of the synthetic values as presented in Figure 7 and Figure 8 below.
4. Implication for Soil Use and Management
Agricultural productivity is sensitive to direct changes in maximum and minimum temperature, precipitation, and GHG concentration. Indirect changes are soil moisture and the distribution and frequency of infestation by pests and diseases. Future climate change will affect crop yield, photosynthesis and transpiration rates, growth rates, and soil moisture availability, through changes of water use and agricultural inputs (herbicides, pesticides, insecticides, fertilizers) [35] . The potential agricultural impacts include extreme weather condition such as floods and drought, soil water management and soil moisture regime [36] .
5. Conclusion
In this study three meteorological parameters from the observed station and AgMERRA reanalysis data for Mount Makulu site―precipitation, minimum and maximum temperature―were simulated using LARS-WG5.5 stochastic weather generator. The results showed that these parameters were modeled with good accuracy. The LARS-WG could be used to generate climate scenarios for the current and future scenarios for Mount Makulu. LARS-WG simulated the monthly mean precipitation, minimum and maximum temperatures which are accurate with the correlation between the observed/AgMERRA reanalysis and g generated monthly means being 0.99. Results showed that the maximum and minimum temperature for Mount Makulu would increase during 2020s and 2055s under SRB1 and SRA1B. The ensemble mean of the HadCM3 and BCM2 GCMs indicated that climate signal for precipitation amount in 2020 and 2055 would increase under observed station data and reduce under AgMERRA reanalysis data. Climate scenarios of more than one climate model are necessary for providing insights into climate model uncertainties as well as developing alternative adaptation and mitigation strategies.
![]()
Figure 7. Shape of the probability distributions using observed station and generated data.
![]()
Figure 8. Shape of the probability distributions using Agmerra reanalysis and generated data.
Acknowledgements
The researchers wish to thank the Agricultural Productivity Programme for Southern Africa (APPSA) under the Zambia Agricultural Research Institute (ZARI) Central Station for financing the publication of this paper. The researchers also wish to thank Prof. Mikhail A. Semenov for the provision of Long Ashton Research Station Weather Generator and license used in this study. Thanks are also extended to Dr. Alexander C. Ruane from National Aeronautics and Space Administration (NASA) and Zambia Meteorological Department (ZMD) for the provision of daily weather data sets.
Conflicts of Interest
The authors declare no conflict of interest.