The Determination of Interfacial Shear Strength in Short Fiber Reinforced Poly Ethylene Terephthalate by Kelly-Tyson Theory ()
1. Introduction
The fiber-matrix interfacial shear strength is the main factor determining the mechanical properties of composite materials. Practically, a stronger composite has the better of adhesive strength between fibers and matrix. The magnitude of the interfacial shear strength is based on the surface properties of both component [1] - [6] . DiBenedetto [7] studied on the effects of different fiber surface treatments to interfacial shear strength of composites. Several researches have studied on the estimation of interfacial shear strength in different approaches, such as Takaku, A [8] , to measure directly the interfacial shear strength (or critical fiber length) between fiber and matrix. Regarding the interfacial shear strength measurement, an alternative Accurate, accurate and economical measurement methods have been studied. To accurately measure the interfacial shear strength of composites, Kelly and Tyson [9] - [14] proposed the equation determine the interfacial shear strength. The well-known Kelly-Tyson model considers the effect of fibers with the fiber length. By assuming a constant shear stress, the interfacial shear strength can be determined through a simple force balance equation of the fragment as shown in Equation (1);
 (1)
(1)
where 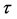 is the interfacial shear strength;
is the interfacial shear strength;
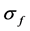 is the ultimate fiber strength at the critical length;
is the ultimate fiber strength at the critical length;
d is the fiber diameter;
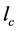 is the fiber critical length.
is the fiber critical length.
The assumption of a constant shear stress was originally used by Kelly and Tyson. In this study, the Kelly-Tyson equation was conducted to find the fiber critical length in order to measure the interfacial shear strength. The equation is shown in equation below (2) [9] - [14] ;
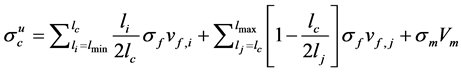 (2)
(2)
The equation is included two main parts as the fiber with sub-critical length shorter than  and fiber with sub-critical length longer than
and fiber with sub-critical length longer than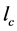 . In addition, in order to more accurately find the critical fiber length, the Kelly-Tyson equation, is modified by adding one more importance factor as the fiber orientation efficiency factor (
. In addition, in order to more accurately find the critical fiber length, the Kelly-Tyson equation, is modified by adding one more importance factor as the fiber orientation efficiency factor ( ). As the modified Kelly-Tyson equation is presented in equation (3) [9] - [14] ;
). As the modified Kelly-Tyson equation is presented in equation (3) [9] - [14] ;
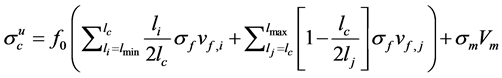 (3)
(3)
In this study, the interfacial shear strength value measuring by the modified Kelly-Tyson equation method was studied the measurement accuracy. Short fiber reinforced poly polyethylene terephthalate (PET) composites were conducted to be measured its interfacial shear strength value. The measuring accuracy by using the modified Kelly-Tyson equation method is compared to the nano-indentation testing method. The results and an influential factor are described. An error in the modified Kelly-Tyson equation is verified to avoid the incorrect measurement when the interfacial shear strength was measured by the modified Kelly-Tyson equation. And in this study, an advance fabricating technique for short fiber reinforced composite as direct fiber feeding process are revealed the interfacial shear strength.
2. Experimental
2.1. Materials
The high quality recycled PET pellets (RPET), which were recycled from PET plastic bottle, were supplied by Negoro Sangyo Co., Ltd. with IV of 0.65 dl/g and molecular weight of 12,600 g/mol. Glass fiber roving (EX-1844) is supplied by Nippon Electric Glass Co., Ltd., Japan. Glass fiber reinforced recycled-PET (GF/ RPET) composites fabricated by direct fiber feeding injection molding (DFFIM) process.
2.2. Specimen Preparation
To study the different interfacial shear strength behavior, the short fiber reinforced recycled-PET (GF/RPET) composites were fabricated. The dumbbell specimens of DFFIM GF/RPET composite samples were fabricated by using direct fiber feeding injection molding process. To fabricate the composites by using DFFIM process, fiber roving is directly fed into venting hole while the neat-re- cycled PET is fed into a hopper; in additional, matrix feeding speed are varied to fabricate a varied fiber loading content GF/RPET composites. By changing matrix feeding speed, the four different amount of fiber loading content of GF/RPET composites were provided to study the interfacial shear strength as 16 wt.%, 28 wt.%, 43 wt.% and 55.2 wt.%. The schematic of DFFIM is shown in Figure 1. The barrel temperatures the locations just before and after the venting hole were set at 260˚C - 280˚C and 250˚C - 275˚C, respectively. The mold temperature was set at 60˚C with 30 s of cooling time. The screw rotational speed was fixed at 150 rpm.
2.3. Tensile Test
For calculate the modified Kelly-Tyson equation, tensile strength of composite sample is required. Regarding to ASTM D683, the specimen is conducted under speed of 1 mm/min with 115 mm grip width.
2.4. Morphology Observation
The observations on phase morphology were carried out by the scanning electron microscope (JEOL/JSM-5200), which was set at 15 kV. Gold was sputtered
![]()
Figure 1. Schematic of direct fiber feeding injection process
onto the specimens for electron conductivity.
2.5. Morphology Observation
The observations on phase morphology were carried out by the scanning electron microscope (JEOL/JSM-5200), which was set at 15 kV. Gold was sputtered onto the specimens for electron conductivity.
2.6. The Fiber Length Measurement
Remained glass fiber were cast on glass slide then observed by optical microscope to measure using image-J software. The number average fiber length (LN) was calculated using following Equation (4) [14] ;
 (4)
(4)
where Ni = The number of fibers of length Li
2.7. Fiber Orientation Index Measurement
The dumbbell specimens were cut at the middle part. To observe at the cross section, the cut dumbbell samples were prepared by using a polishing machine. After polishing, the cross-section of dumbbell was photographed by using an optical microscope in order to observe the fiber orientation into its specimen. An example of optical photograph was shown in Figure 2(a). Two kinds of fiber can be found in the cross-section as a circle fiber shape and elliptical fiber shape. The circle fiber shape determines if fiber is perpendicular to the section plane. On the other hand, the elliptical fiber shape indicates if fiber is at an angle to the section plane. The elliptical fiber shape was mark the cross section to know the θ as shown in Figure 2(b). Fiber orientation index can be calculated by using as following Equation (5) [14] [15] ;
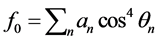 (5)
(5)
When θn = cos−1(b/a)
2.8. Nano-Indentation Test
The dumbbell specimens was cut at middle part then it was polished to decrease the thickness as 200 mm. the prepared sample was measured the interfacial shear strength by Agilent Technologies Nano Indenter G200. The maximum load and pushed speed were 400 mN and 2 mN/s, respectively.
![]()
Figure 2. (a) An example of optical photograph at cross section of dumbbell specimen for measuring fiber orientation, and (b) Definition and determination of the fiber orientation [16] .
3. Results and Discussion
To verify the accuracy of the modified Kelly-Tyson equation, the nano-indenta- tion test was carried out. The glass fiber reinforced recycle-PET composite made by direct fiber feeding injection molding process (DFFIM GF/RPET) was measured by using nano-indentation test. The result from the nano-indentation test indicates that DFFIM GF/RPET has the interfacial shear strength value as 25.3 MPa. The DFFIM GF/RPET samples were calculated the interfacial shear strength by the modified Kelly-Tyson equation. The four different fiber loading content of 16 wt.%, 28 wt.%, 43.3 wt.% and 55.2 wt.% DFFIM GF/RPET composites were measured by the modified Kelly-Tyson equation. The required and measured data were shown in Table 1. In this calculation, the fiber strength was assumed as 1500 MPa [17] . In the four different fiber loading content measuring by the equation case, the calculated interfacial shear strength values are different. Indeed using the same material, the calculated interfacial shear strength value supposed to be same. Thus, using the different fiber loading contents sample should not change the interfacial shear strength values of composite. The calculated interfacial shear strength value tend to be decreased when amount of fiber loading content increase, respectively. The measured interfacial shear strength values of 16 wt.%, 28 wt.%, 43.3 wt.% and 55.2 wt.% GF/RPET composite were compared to the result of its nano-indentation testing value, which there are percent difference in interfacial shear strength values as −1.2%, −8.0%, −35.7% and −31.6%, respectively. It showed that at 16 wt.% fiber loading content is the highest accurate result when compare with its nano-indentation result. The cal-
![]()
Table 1. The required and measured data of different fiber loading content GF/RPET composites for calculating the interfacial shear strength by the modified Kelly-Tyson equation. And the t comparison between using the modified Kelly-Tyson equation and nano-indentation.
culated lc values increase when the calculation is conducted under the high fiber loading content sample. The average fiber orientation values of all samples exhibit to be almost similar; nevertheless, SEM photographs are contradictory to the average fiber orientation results. As SEM photographs of dumbbell’s cross section at central position of DFFIM GF/RPET composites were shown in Figure 3.
The SEM photographs indicate that there are a horizontally aligned fiber area especially at the central position; furthermore, the size of the horizontally aligned fiber area tend to increase with the fiber loading content increasing. This horizontally aligned fiber area might be very sensitive on the strength of composite; furthermore, it must very affect to the measuring by the modified Kelly- Tyson equation. Because at this horizontally aligned fiber area, there fiber lay down on surface, so the fiber cannot provide a good reinforced efficiency. The fibers lay down at the horizontally aligned fiber area caused there is a strength pre area being very low. This cause must affects to the measured accuracy. Regarding this horizontally aligned fiber area, the DFFIM GF/RPET samples were more investigated the fiber orientation value on each parts of dumbbell specimen. To more observe the horizontally aligned fiber on dumbbell specimen, the thoroughly measured positions in dumbbell sample are shown in Figure 4, and the relationship between fiber orientation values on normalized thickness of specimens is shown in Figure 5. The results indicate that at the central position the fiber orientation values are poor as compared with skin position. Because in the central core region, the fiber orientation is normally forced by the orientation imposed by the gate. Usually the melt develops from the gate into the mold, and this disturbed flow tends to align fibers perpendicular to the flow direction. In the injection-flow edge, the orientation is caused by the fountain flow at the flow front, and this generally aligns fibers along the flow direction. This shearing flow between the wall and melted polymer results in preferential alignment of the fibers approximately along the flow direction [18] . In addition, the fiber orientation values become to be wore when fiber loading content increase, respectively. Regarding to this results, it can said that the average fiber orientation value is not good enough for using in the modified Kelly-Tyson equation, if it is conducted with high fiber loading content sample. Because the poor fire orientation at central position resulted in the increasingly incorrect calculation by using the modified Kelly-Tyson equation. However, using the modified Kelly-Tyson
![]()
Figure 3. SEM photographs at dumbbell’s cross section of DFFIM GF/RPET composites (a) 16 wt.%; (b) 28 wt.%; (c) 43.3 wt.% and (d) 55.2 wt.%.
![]()
Figure 4. The measured positions of fiber orientation in dumbbell sample.
equation method at the low fiber loading content sample provides the very accurate the interfacial shear strength value. From these results, it can be concluded that to measure the interfacial shear strength by the modified Kelly-Ty- son equation, it should avoid a sample containing high fiber agglomeration or high fiber loading content.
4. Conclusion
The modified Kelly-Tyson equation method accurately provides the interfacial
![]()
Figure 5. The relationship between Orientation factors on normalized thickness of DFFIM GF/RPET composite.
shear strength value, if it is conducted with the sample without fiber agglomeration. So the high fiber loading content sample should be avoided to get the more accurate result. The fiber agglomeration into specimens extremely resulted in the incorrect measurement of the interfacial shear strength value by the modified Kelly-Tyson equation method. The fiber agglomeration factor must be considered its influence on the measuring for improving the equation effectiveness.