A Method to Determine the Margins of High Sea Ice Concentration Using AMSR-E Passive Microwave Imagery ()
1. Introduction
Arctic sea ice is one of the most important parameters in the global climate system, and is experiencing profound declines in areal extent, thickness, and ice age [1] [2] [3]. This rapid change in sea ice forms part of a series of Arctic climate transitions, which include shifts in the atmospheric circulation with concomitant changes in air temperature and an increase in melt-water storage in the upper Arctic Ocean [4] [5] [6] [7]. The IPCC’s fifth Assessment Report suggests that Arctic sea ice will disappear during summer of 2100 [8]. Clearly, model results overestimate the change of sea ice because some physical processes and parameters are not fully know for accurately predicting the information of ice pack [9]. Therefore, knowledge of any information of the Arctic ice is of very importance for modeling and predicting the global climate.
The position and motion of the ice margins are important parameters for sea ice dynamics, thermodynamics and climate research [10]. Sea ice concentration is a useful parameter to define the ice margins. For example, the generally high concentration of ice margins in the Arctic Basin, the Beaufort Sea and Chukchi Sea can be taken as 96% [11]. The marginal ice zone (MIZ) is a mixed region of sea ice and seawater and compressed ice region have generally high concentration. These two regions have different effects on climate and sea water. There is no apparent boundary between MIZ and compressed ice region, because sea ice concentration generally exhibited a gradual change in these regions. The margins of compressed ice region (ice margins) were investigated by using passive microwave imagery in this paper. The margin will to be determined by using a new method depending on the features of remote sensing data.
Satellite remote sensing of the polar ice caps is one of the most important tools to determine the ice margins. Optical sensors can provide high resolution image, however it is only useful for sea ice monitoring under clear sky conditions and during the day [12]. Passive microwave sensors are alternative choice for observing sea ice since microwaves can penetrate heavy clouds and precipitations [13]. Therefore a large number of microwave radiation data are used in the study of sea ice concentration, sea ice extent and sea ice types and so on [3] [14] [15] [16].
The Advanced Microwave Scanning Radiometer?EOS (AMSR-E) sensor on board EOS-Aqua, which was launched by NASA in May 2002, measures microwave radiances at six frequencies, including 6.925, 10.65, 18.7, 23.8, 36.5 and 89.0GHz at both horizontal and vertical polarizations. It provides a significant improvement in our capability for monitoring the sea ice cover. The Moderate Resolution Imaging Spectroradiometer (MODIS) acquires data in 36 different spectral bands (0.4 - 14.4 μm) and its spatial resolution of the bands ranges from 250 m to 1km. Because MODIS images can provide an unambiguous determination of the ice edge, it was acquired to verify the position of sea ice edge [17], accuracy of sea ice concentration [18] and the detection of sea ice leads [19].
In the study of the ice coverage, the brightness temperature, which comes from the open water, from the ice-covered area, or from a mix of both, can be expressed in terms of the relative contribution from each surface type by a linear mixing formulation [13]. In winter, there is a high correlation between the horizontal-polarized and vertical-polarized brightness temperatures at 36.5GHz (HV36.5), which were approximately distributed in a line in two-dimensional plot. On the one hand, sea water and melt pond have similarly microwave radiation characteristics [20], so it is impossible to distinguish between melt pond and sea water using brightness temperature. On the other hand, there are little 100% pixel during summer time. For these two reasons, the HV36.5 data lost its distinct features in the summer. Therefore, HV36.5 data is used only in spring, autumn and winter when sea ice concentration is retrieved.
Although the position of the ice margins is one of principal features in passive microwave imagery, there was no good method for recognition until now. A method to detect ice margins with HV36.5 image is presented here. The method focuses on the detection of the edge, where sea water has weakly affected to the microwave radiation. The used brightness temperature data and proposed method are elaborated in Section 2. At same time, a new parameter to distinguish ice margins in passive microwave image is used. In Section 3, the results are examined and validated.
2. Methods
2.1. AMSR-E Dual-Polarized Brightness Temperature at 36.5 GHz
The basic radiative transfer equation that expresses the brightness temperature 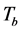 in terms of surface emission, accounting for atmospheric and other effects is given by [13]
in terms of surface emission, accounting for atmospheric and other effects is given by [13]
 (1)
(1)
where the first term is the dominant term that represents radiation received directly from the earth’s surface, 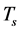 is the physical temperature of the surface,
is the physical temperature of the surface, 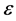 is the surface emissivity, and
is the surface emissivity, and 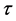 is the atmospheric opacity. The second term
is the atmospheric opacity. The second term 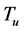 represents radiation directly from atmosphere. The third term represents downwelling radiation from the atmosphere reflected by the surface of the earth. The last term is the radiation from outer space which is a negligible additive contribution.
represents radiation directly from atmosphere. The third term represents downwelling radiation from the atmosphere reflected by the surface of the earth. The last term is the radiation from outer space which is a negligible additive contribution.
Below 40GHz only water vapor has weakly absorbing at 22 GHz, but atmospheric moisture content at Arctic is very small [11]. So the net effect of the atmospheric temperature is very small and is ignored. The brightness temperature Tb could be expressed as a function of the sea ice temperature Ti and the water temperature Tw,
 (2)
(2)
where C is sea ice concentration, εi and εw are sea ice microwave emissivity and sea water microwave emissivity, respectively. Equation (2) is a basic equation in sea ice concentration algorithm, such as ABA, BBA and NASA Team [13]. The National Snow and Ice Data Center (NSIDC) of the USA provides the 12.5 × 12.5 km gridded AMSR-E brightness temperature and sea ice concentration retrieved using the ABA and NT2 algorithms at the same grid (http://nsidc.org/data/amsre). Figure 1(a) shows the horizontal-polarized brightness temperature versus vertical-polarized brightness temperature observed at 36.5 GHz on March 1, 2009. In Figure 1(a), the observed data distributed along the straight line AD with a slope 0f 0.94 were corresponding to nearly 100% ice concentration [16].
When the sea ice concentration equals 1, Equation (2) can be written as
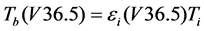 (3a)
(3a)
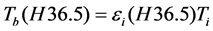 . (3b)
. (3b)
where H36.5 denotes the horizontal-polarized brightness temperature observed at 36.5 GH, V36.5 denotes the vertical-polarized brightness temperature observed at 36.5 GHz.
From Equation (3b) and Equation (3a), for the sea surface with nearly 100% ice concentration we have:
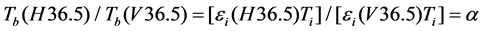 (4)
(4)
or
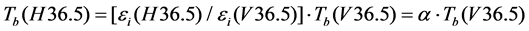 (5)
(5)
where  is the ratio of the horizontal-polarized emissivity to the vertical-polarized emissivity. For simplicity, we call
is the ratio of the horizontal-polarized emissivity to the vertical-polarized emissivity. For simplicity, we call 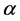 as the dual-polarized emissivity ratio in this study.
as the dual-polarized emissivity ratio in this study.
From Equation (4), we know that the dual-polarized emissivity ratio 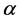 is approximately equal to the ratio between horizontal-polarized and vertical- polarized brightness temperatures of sea surface with nearly 100% ice concentration, as shown as the slope of straight line AD in Figure 1(a).
is approximately equal to the ratio between horizontal-polarized and vertical- polarized brightness temperatures of sea surface with nearly 100% ice concentration, as shown as the slope of straight line AD in Figure 1(a).
However, for all area in Arctic Ocean, the ratio  cannot be determined by the ratio of dual-polarized brightness temperatures in Equation (4), due to the less sea ice concentration and influence from sea water on brightness temperature in Equation (2). The spatial distribution of
cannot be determined by the ratio of dual-polarized brightness temperatures in Equation (4), due to the less sea ice concentration and influence from sea water on brightness temperature in Equation (2). The spatial distribution of  is shown in Figure 1(b). The ratio is relatively small (less than 0.73) with sparse contours in open water. The ratio clearly changes at the marginal ice zone (MIZ) from 0.73 to 0.92 and the contours become denser. In the regions covered with sea ice, the most of
is shown in Figure 1(b). The ratio is relatively small (less than 0.73) with sparse contours in open water. The ratio clearly changes at the marginal ice zone (MIZ) from 0.73 to 0.92 and the contours become denser. In the regions covered with sea ice, the most of 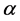
![]() (a) (b) (c)
(a) (b) (c)
Figure 1. (a) Scatter plot of HV36.5GHz (Note, the slope of line AD is 0.94); (b) Spatial distribution of the ratio about H36.5 and V36.5GHz; c histogram of the ratio about H36.5 and V36.5GHz.
values change from 0.92 to 0.96 and the contours are also very sparse. Figure 1(b) also indicates that there is no difference between multiyear ice and first year ice for![]() . Because of mixing of the sea ice and seawater, the
. Because of mixing of the sea ice and seawater, the ![]() change is very large. So there should be a threshold ratio
change is very large. So there should be a threshold ratio ![]() at ice margins: When
at ice margins: When ![]() is larger than
is larger than![]() , the
, the ![]() is mainly affected by sea ice and dual-polarized brightness temperature data distribute along a straight line; otherwise the
is mainly affected by sea ice and dual-polarized brightness temperature data distribute along a straight line; otherwise the ![]() is significantly influenced by sea water. Therefore,
is significantly influenced by sea water. Therefore, ![]() is the threshold ratio used to distinguish the ice margins.
is the threshold ratio used to distinguish the ice margins.
Figure 1(c) shows the frequency histogram of ![]() (from 0.600 to 0.970) for the whole Arctic region, the interval is 0.001. Two peaks appear: the left one corresponds to open water, and the right one corresponds to the sea surface with high sea ice concentration. In the sea ice covered regions, the value of
(from 0.600 to 0.970) for the whole Arctic region, the interval is 0.001. Two peaks appear: the left one corresponds to open water, and the right one corresponds to the sea surface with high sea ice concentration. In the sea ice covered regions, the value of ![]() is limited from 0.92 to 0.96 as shown in Figure 1(b), but the frequency of
is limited from 0.92 to 0.96 as shown in Figure 1(b), but the frequency of ![]() with the values between 0.92 and 0.96 exhibits obvious change as shown in Figure 1(c).
with the values between 0.92 and 0.96 exhibits obvious change as shown in Figure 1(c).
2.2. Definition of Contrast Ratio
There is no apparent boundary at ice margins because sea ice concentration is gradually changing from open water to ice margins. In this section, a new parameter, called as the contrast ratio, is used to quantitatively calculate the threshold ratio![]() . Contrast ratio full use of the gradient of pixel and the number of pixel to outstanding ice margins [21] . First, the frequency
. Contrast ratio full use of the gradient of pixel and the number of pixel to outstanding ice margins [21] . First, the frequency ![]() of each
of each ![]() from 0.600 to 0.970 is calculated for the whole Arctic region, as shown in Figure 1(c). Second, the difference of
from 0.600 to 0.970 is calculated for the whole Arctic region, as shown in Figure 1(c). Second, the difference of ![]() between each grid and its neighboring grids needs to be calculated. If the difference is larger than a threshold value
between each grid and its neighboring grids needs to be calculated. If the difference is larger than a threshold value![]() , the frequency
, the frequency ![]() is calculated. Here
is calculated. Here ![]() denotes the frequency of
denotes the frequency of ![]() with the difference larger than threshold value
with the difference larger than threshold value![]() . Finally, the contrast ratio
. Finally, the contrast ratio ![]() is defined as
is defined as
![]() (6)
(6)
The definition of ![]() includes two important information about
includes two important information about![]() : the change in the value of
: the change in the value of ![]() and the change in its frequency. Therefore,
and the change in its frequency. Therefore, ![]() can represent the features of
can represent the features of ![]() at the ice margins.
at the ice margins.
The threshold value ![]() can be chosen arbitrarily according to
can be chosen arbitrarily according to![]() , because it only changes the value of
, because it only changes the value of ![]() but it does not alter the curve shape of the contrast ratio. In this paper, 0.005 is chosen as threshold value
but it does not alter the curve shape of the contrast ratio. In this paper, 0.005 is chosen as threshold value![]() . In some grids,
. In some grids, ![]() is higher than the threshold value
is higher than the threshold value ![]() in several neighboring grids; so
in several neighboring grids; so ![]() could be larger than 1. The gradient of
could be larger than 1. The gradient of ![]() can quantitatively describe the change of
can quantitatively describe the change of ![]() and can be written as
and can be written as
![]() (7)
(7)
The contrast ratio ![]() (black line) and its gradient (red line) are shown in Figure 2(a). Here Contrast ratio
(black line) and its gradient (red line) are shown in Figure 2(a). Here Contrast ratio ![]() decreases rapidly from 1.4 to less than 0.5 for
decreases rapidly from 1.4 to less than 0.5 for ![]() values between 0.90 and 0.93, while the most abrupt changes occur at 0.92. Thus, when the ratio
values between 0.90 and 0.93, while the most abrupt changes occur at 0.92. Thus, when the ratio ![]() of dual-polarized brightness temperatures is
of dual-polarized brightness temperatures is
equal to 0.92, the dual-polarized emissivity ratio reaches its threshold ratio of![]() . In Figure 2(b), two zero-crossing lines are shown in scatter plot. The slope of green line is 0.92 and the slope of red line is 0.97. It is apparent that the data points linearly distribute between the green line and red line when the
. In Figure 2(b), two zero-crossing lines are shown in scatter plot. The slope of green line is 0.92 and the slope of red line is 0.97. It is apparent that the data points linearly distribute between the green line and red line when the ![]() is larger than 0.92. So the value of
is larger than 0.92. So the value of ![]() can be derived using
can be derived using ![]() and
and![]() , as shown in Figure 2(c). The value of
, as shown in Figure 2(c). The value of ![]() before June showed relative stability, fluctuating mainly between 0.92 and 0.93.
before June showed relative stability, fluctuating mainly between 0.92 and 0.93.
3. Validation and Discussion
3.1. Validation
The threshold ratio ![]() is determined using contrast ratio of brightness temperature in Section 2 and its value changed around 0.92 before June. In order to verify that
is determined using contrast ratio of brightness temperature in Section 2 and its value changed around 0.92 before June. In order to verify that ![]() ≈ 0.92 is correct, we will compare the positions of sea ice margin, obtained from microwave image and MODIS images, respectively. MODIS images could be used to verify the position of sea ice edge, sea ice concentration and sea ice leads [19] [16]. Band 2 of the MODIS sensor (841 - 876 nm) has a spatial resolution of 250 m. So MODIS image of band 2 could be used to validate the ice margins. For validation, the chosen MODIS images must be those observed in very clear days to eliminate the influence of clouds.
≈ 0.92 is correct, we will compare the positions of sea ice margin, obtained from microwave image and MODIS images, respectively. MODIS images could be used to verify the position of sea ice edge, sea ice concentration and sea ice leads [19] [16]. Band 2 of the MODIS sensor (841 - 876 nm) has a spatial resolution of 250 m. So MODIS image of band 2 could be used to validate the ice margins. For validation, the chosen MODIS images must be those observed in very clear days to eliminate the influence of clouds.
Zhao and Ren [21] determined the threshold between the sea ice and sea water in the aerial image using contrast ratio. Then sea ice edge, sea ice concentration and sea ice size are studied in aerial image. So this method can also used in the MODIS images to discriminate ice and water because of their highly contrasted albedo. Figure 3 show four images of MODIS at spring of 2009 (Top pictures), their discriminated pictures (Middle pictures) and corresponding sea ice concentration pictures (Bottom pictures). White and black pixels in the middle pictures represent sea ice and sea water, respectively.
The pixels of bottom pictures of Figure 3 are 12.5 × 12.5 km, which is composed of 2,500 MODIS pixels, so sea ice concentration are the percentage of ice pixels among the 2,500 MODIS pixels. The white contour demotes the pixel with
![]() Barents Sea Chukchi Sea South Bering strait North Bering strait
Barents Sea Chukchi Sea South Bering strait North Bering strait
Figure 3. MODIS images, top pictures; Ice-water discriminated pictures, middle pictures; sea ice concentration retrieved by MODIS images, bottom. NOTE: The MODIS images down load from http://ladsweb.nascom.nasa.gov/.
96% sea ice concentration and the green contour denotes the pixel in which the ratio ![]() is equal to 0.92. In the Section 2, we know that the threshold ratio
is equal to 0.92. In the Section 2, we know that the threshold ratio ![]() fluctuates mostly between 0.92 and 0.93. Calculation indicated that an average sea ice concentration corresponding to
fluctuates mostly between 0.92 and 0.93. Calculation indicated that an average sea ice concentration corresponding to ![]() is 0.96. The Figure 3 shows that the red contour is very closed to green contour and their shape is very similar to each other.
is 0.96. The Figure 3 shows that the red contour is very closed to green contour and their shape is very similar to each other.
Table 1 lists the average curve separation (ACS), mean absolute difference (MSD), and root mean square error (RMS) between the red contour and green contour in the four regions of Figure 3. The maximum of ACS, MSD and RMS is 10.5 km, 10.0 km, 6.5 km, respectively, which are well lower than the size of AMSR-E grid (12.5 km). Figure 4 shows the distance histograms of these four ice margins and shows that the majority of the distances are less than 12.5 km.
Figure 3 and Figure 4 indicate that the distance between red contour and green contour is relatively small in the ocean, except few regions with distance larger than 12.5 km. This phenomenon is caused mainly by three reasons. Firstly, cloud could not be distinguished from sea ice in the MODIS image. Secondly, the melted pond and sea water cannot be distinguished in microwave image. Finally, the MODIS shows the image at a moment, however; AMSR-E shows the brightness temperature at another moment. In addition, the movement of sea ice may cause the difference between MODIS and AMSR-E in sea ice margins.
![]()
Figure 4. Histograms of distances between ice margins derived from AMSR-E and MODIS.
![]()
Table 1. Statistical analysis of sea ice margins derived from AMSR-E and MODIS. ACS is average curve separation, MSD is mean absolute difference and RMS is root mean square.
3.2. Discussion
A method for determining the ice margins is given in this paper. The threshold ratio ![]() can be used to distinguish the ice margins. Here
can be used to distinguish the ice margins. Here ![]() is the dual-pola- rized emissivity ratio at 36.5 GHz in the sea ice coverage area. When sea ice concentration is close to 1, the dual-polarized brightness temperatures can be plotted along a line that crosses the origin of coordinates in the scatter plot, as shown in Figure 1(a). At the same time, the ratio of dual-polarized brightness temperatures is unaffected by the type of sea ice and its value changes mostly from 0.92 to 0.96 in the sea ice coverage area. However, under the influence of sea water, a rapid change of
is the dual-pola- rized emissivity ratio at 36.5 GHz in the sea ice coverage area. When sea ice concentration is close to 1, the dual-polarized brightness temperatures can be plotted along a line that crosses the origin of coordinates in the scatter plot, as shown in Figure 1(a). At the same time, the ratio of dual-polarized brightness temperatures is unaffected by the type of sea ice and its value changes mostly from 0.92 to 0.96 in the sea ice coverage area. However, under the influence of sea water, a rapid change of ![]() occurs from open water to sea ice margins. All these characteristics can be used to determine a threshold ratio
occurs from open water to sea ice margins. All these characteristics can be used to determine a threshold ratio![]() , which defines margins of high sea ice concentration coverage. The contrast ratio of dual-polarized brightness temperature is used to determine the
, which defines margins of high sea ice concentration coverage. The contrast ratio of dual-polarized brightness temperature is used to determine the![]() . The study found that the
. The study found that the ![]() changes around 0.92 and the data of dual-polarized brightness temperatures distribute along a straight line in scatter plot when
changes around 0.92 and the data of dual-polarized brightness temperatures distribute along a straight line in scatter plot when ![]() is larger than
is larger than![]() .
.
The position of the ice margins not only is a principal feature in microwave image, but also has an important significance in sea ice concentration retrieving. Sea ice concentration retrieved from passive microwave data over the high concentration Arctic sea ice has shown biases which are about one magnitude larger than the true variability [22]. In the same sea ice concentration algorithm, using different parameters may lead to larger differences of the sea ice concentration. For example, the Bootstrap Algorithm can be used to calculate the sea ice concentration once the line AD is determined in Figure 1(a). The slope of the line AD is 1.00 or 1.04 in the Bootstrap Algorithm, and the line AD does not cross the origin of the coordinates. However, in this paper, not only the line AD crosses the origin but also its slope changes between 0.92 and 0.96. So it is very important that the position of the ice margins need to be verified in sea ice concentration algorithm according to the features of dual-polarized brightness temperature at 36.5 GHz.
The ice margins are determined not only by sea ice concentration, which are retrieved by brightness temperature, but also by the ratio of dual-polarized brightness temperatures at 36.5 GHz. One of the advantages is that new method avoids the impact of error of sea ice concentration retrieval. Validation results indicate that this new method can be used to determine the ice margins of passive microwave imagery. So this method has a good practical and applied value.
4. Conclusions
The Arctic is undergoing rapid change, such as sea ice extent decreases and sea ice concentration decline in recent years. These results leaded that marginal ice zone (MIZ) greatly expanded and MIZ became an important climatic factor in the study on ocean-atmosphere interactions. The position of ice margins is very important in studying MIZ. A method for determining the ice margins is developed using the features of dual-polarized brightness temperatures at 36.5 GHz and a new parameter (contrast ratio) is used in the method. The specific conclusions are given as follows:
(1) The data of dual-polarized brightness temperature at 36.5 GHz distribute along a straight line in scatter plot, which are corresponding to nearly 100% sea ice concentration in Arctic, and the line crosses the origin of the coordinates. The slope of the line is equal to the ratio of horizontal emissivity to vertical emissivity of ice and its value changes between 0.92 and 0.96.
(2) From open water to sea ice covered area, the parameter of contrast-ratio can show the changing features of the ratio of dual-polarized brightness temperature at 36.5 GHz. At the influence of sea water, the contrast ratio rapidly changes at the high sea ice concentration margins and its gradient appears extreme value when the ratio of dual-polarized brightness temperature changes around 0.92. In the scatter plot, the data of dual-polarized brightness temperature at 36.5 GHz apparently distribute along a straight line in scatter plot when their ratio larger than 0.92. Therefore, the threshold value is 0.92 which determine the ice margins in Arctic Ocean.
Acknowledgements
The authors gratefully acknowledge the support for this work under the National Natural Science Foundation of China (41406208), the Scientific and Youth Science Funds of Shandong Academy of Sciences, China (2013QN042), the Open Research Fund of the State Oceanic Administration of the People’s Republic of China Key Laboratory for Polar Science (3KP201203). We also acknowledge AMSR-E data and MODIS image provided by the National Snow and Ice Data Center and NASA.