Evaluation for the Performance of the CORDEX Regional Climate Models in Simulating Rainfall Characteristics over Mbarali River Catchment in the Rufiji Basin, Tanzania ()
1. Introduction
The General Circulation Models (GCMs) are currently the most advanced tools currently available for simulating the response of the global climate system, to increased greenhouse gas concentration in the atmosphere [1] [2] . They use variety of fluid dynamical, chemical, and biological equations to describe important physical elements and processes in different components of climate systems: atmosphere, oceans, cryosphere, and land surface [3] . One disadvantage of GCMs is that, they have the low spatial resolution which is restricted in the range of 100 - 300 km [4] . This resolution is too small to provide useful information about climate change for impact studies on hydrology, ecosystem services, and other landscape and agriculture related matters [4] [5] [6] [7] [8] . In order to bridge the gap between what is supplied by the GCMs and what is required for impact studies; scientist has developed two types of downscaling techniques: statistical and dynamical downscaling.
Dynamical downscaling is the most appropriate downscaling technique which provides better representation of the orographic effect on climate variables. Its main approach is based on nesting high resolution, Regional Climate Model (RCM) and runs it using boundary condition from the GCM [9] . Generally dynamical downscaling is computationally expensive. At present, many collaboration projects are generating climate simulation from dynamical downscaling for model inter-comparisons and impact assessments. These projects include the Coordinated Regional Climate Downscaling Experiment (CORDEX) that produces dynamical downscaled climate simulation for all continents, the North American Regional Climate Change Assessment Program (NARCCAP) that provides high resolution climate simulation for United States, northern Mexico, and Canada [10] . These projects have made available large number of high resolution climate simulations that can be used for impact assessments.
However, before using climate simulation from dynamical downscaling, it is appropriate to evaluate their performance at different spatial scales. This is of the most important for choosing the appropriate climate model to be used for impact assessment at location since the performance of the dynamical downscaled data differs from location to location and from one RCM to another [1] .
Several studies have evaluated the performance of the output from dynamical downscaled data especially those generated by CORDEX [1] [11] [12] [13] . Shong- we et al., (2015), examined the performance of the output from CORDEX RCMs in simulating precipitation over Southern Africa. They found that the RCMs adequately captured the reference precipitation probability density functions, with a few showing a towards excessive light rainfall events. [14] assessed the performance of CORDEX regional climate model to simulate precipitation climatology in East Asia. They found that CORDEX RCMs can simulate the annual cycle, seasonal mean, and inter-annual variability of rainfall acceptably. Very recently Luhunga et al. (2016) evaluated the performance of the CORDEX RCMs in simulating minimum air temperature and maximum air temperature and rainfall over Tanzania. They evaluated CORDEX RCMs against observed station data that are scattered over complex topographical terrain. They found that CORDEX RCMs perform differently in simulating rainfall over different regions in Tanzania.
Although the evaluation by Luhunga et al. (2016) was comprehensive at station scale throughout the country but there is need to evaluate the performance of the CORDEX RCM at catchment scale. This study is devoted to evaluate the performance of the CORDEX RCMs to simulate rainfall climatology over Mbarali River catchment. The output from this study is intended to be used for climate change impact assessment on hydrology over the Mbarali River catchment.
2. Data and Methodology
2.1. Study Aea
The united republic of Tanzania is in East Africa between latitudes 1˚S and 12˚S and longitudes 29˚E to 41˚E. It has a tropical type of climate but has regional variation of its climate due to high regional heterogeneity that covers a land area of 885,800 km2 that extends from the Indian Ocean coastline to more than 1000 km inland [15] . Based on the land morphology Tanzania has nine basins that includes Lake Victoria, Wami-Ruvu, Lake Tanganyika, internal drainage, Pangani, Rufiji, Lake Nyasa, Rukwa, and Ruvuma basins [16] . The Mbarali River catchment that covers an area of 1530 Km2 within the Upper Great Ruaha is located in the Rufiji basin in the south-eastern highland of Tanzania along latitude 7˚ and 9˚ and longitude 33.8˚ and 35˚ (Figure 1). The River catchment is at an altitude ranging from 1000 to 1800 meters above sea level. The climate over Mbarali River catchment is controlled by the movement of the Inter-Tropical Convergence Zone (ITCZ) which becomes active 3 - 4 weeks after the overhead sun [17] . The catchment receives unimodal rainfall due to single passage of the ITCZ. Seasonal rainfalls are in the ranges of 450 to 650 mm that starts from October through to April or May [1] . The average temperature in the catchments ranges from 25˚C and 30˚C. The dominant land use activities in the catchment include agriculture for production of crops and livestock keeping. It is estimated that over 83% of residents are engaged in agriculture and paddy production being the major food and cash crop.
2.2. Data
2.2.1. Climate Data from the Model
This study uses rainfall simulated data from four regional climate models in the Coordinated Regional Climate Downscaling Experiment (CORDEX) database. These data were obtained from http://cordexesg.dmi.dk/esgf-web-fe/. The output from CORDEX RCMs are quality controlled and can be used according to the term of use (http://wcrp-cordex.ipsl.jussieu.fr/). Monthly rainfall data for the period of 34 years (1971-2005) were derived from four CORDEX RCMs listed in Table 1. It should be noted that all CORDEX RCMs are set to 0.44˚ by 0.44˚ spatial resolutions. This corresponds to 50 km by 50 km. The CORDEX RCMs and their driving GCMs written in short forms as (CNRM) for the CNRM- CERFACS-CNRM-CM5, (ICHEC) for the ICHECEC-EARTH and(MPI) for the MPI-M-MPI-ESM-LR (Table 1).
![]()
Figure 1. Study area Mbarali River sub catchment.
![]()
Table 1. Indicate the CORDEX-RCMs and their driving GCMs used in this study.
2.2.2. Climate Data Era Interim Reanalysis
One of the main problems in evaluating the RCM simulations over Africa is the lack of the quality of observed data set at suitable temporal and spatial resolution [18] . There are no observed meteorological station networks in the Mbarali River catchment. The nearby meteorological stations are found in Mbeya and Iringa regions. This leads to use monthly rainfall data from the ERA-Interim re-analy- sis. The details on how these data are produced and quality controlled the reader may consult [18] . Rainfall data for the period from 1979-2015 are used to compare with model simulation over the Mbarali River catchment.
2.3. Analysis
The area weighted average method was used to calculate the average rainfall from the CORDEX RCMs and from ERA-Interim reanalysis over the entire Mbarali River catchment (latitude 7˚ and 9˚ and longitude 33.8˚ and 35˚). Com- parison between rainfall data from CORDEX RCMs and ERA-Interim reanalysis was done to test the ability of the CORDEX RCMs to reproduce the annual cycles, interannual variability, annual total and trends of rainfall as presented by the ERA-Interim reanalysis.
Evaluation Criteria for Model Performance
Statistical method for evaluation of model performance that includes the Root Mean Square Error (RMSE), Mean Error (ME), Pearson correlation coefficient (r), Mean, median, Standard Deviation and the Mann Kendall Test is used for trend analysis presented in the following equations.
 (1)
(1)
 (2)
(2)
 (3)
(3)
where RCM and ERA are, the RCMs simulated and ERA-interim reanalysis rainfall data respectively, while i is the RCMs simulated and ERA-interim reanalysis pairs and N is the number of such pairs.
2.4. Trends in Rainfall
Mann-Kendall Trend Test and Estimation of Gradient of Trend
Among of the statistical trend analysis methods that have been mostly used to detect trends in meteorological time series is a Mann-Kendall trend test which is non-parametric [19] . It is a rank-based procedure, which is robust to the influence of outliers and extreme values. With this test, the null hypothesis H0 states that, there is no trend in data. This means that the data is independent and identically distributed random, this is tested against the alternative hypothesis H1 which assume that there is a trend. The Mann Kendall test is calculated by considering the time series of n data points and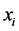 , and
, and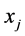 , as two subsets of data where
, as two subsets of data where 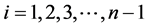 and
and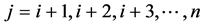 . The values are evaluated as an ordered time series. Each data value is compared with all subsequent data values and if a data value from a later time period is higher than a data value from an earlier time period, the statistic S is incremented by 1. Likewise, if the data value from a later period is lower than a data value sampled earlier, S is decremented by 1. The net result of all such increments and decrements yields the final value of S. The Mann-Kendall S Statistic is computed using Equation (4), and the test of significant is computed using Equation (5):
. The values are evaluated as an ordered time series. Each data value is compared with all subsequent data values and if a data value from a later time period is higher than a data value from an earlier time period, the statistic S is incremented by 1. Likewise, if the data value from a later period is lower than a data value sampled earlier, S is decremented by 1. The net result of all such increments and decrements yields the final value of S. The Mann-Kendall S Statistic is computed using Equation (4), and the test of significant is computed using Equation (5):
 (4)
(4)
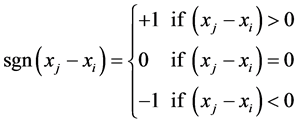 (5)
(5)
where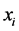 , and
, and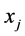 , are the annual values in years i and j,
, are the annual values in years i and j,  respectively.
respectively.
When the sample size n is less than 10, the value of  , is compared directly to the theoretical distribution of S derived by Mann and Kendall (calculated using Equations (4) and (5)) and is asymptotically normal [20] . The two-sided test is used, at certain probability level H0 is rejected in favour of H1 if the absolute value of S equals or exceeds a specified value Sα/2, where Sα/2 is the smallest S which has the probability less than α/2 to appear in case of no trend. A positive value of S designates an “increasing trend”; likewise, a negative designates descending trend.
, is compared directly to the theoretical distribution of S derived by Mann and Kendall (calculated using Equations (4) and (5)) and is asymptotically normal [20] . The two-sided test is used, at certain probability level H0 is rejected in favour of H1 if the absolute value of S equals or exceeds a specified value Sα/2, where Sα/2 is the smallest S which has the probability less than α/2 to appear in case of no trend. A positive value of S designates an “increasing trend”; likewise, a negative designates descending trend.
For 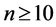 the statistic S is approximately normally distributed with the mean and variance as follows:
the statistic S is approximately normally distributed with the mean and variance as follows:
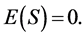 (6)
(6)
The variance , for the S statistic is defined as follows:
, for the S statistic is defined as follows:
![]() (7)
(7)
in which![]() , denotes the number of ties to the extent i. The summation term in the numerator is used only if the data series contains tied values. The standard test statistic Zs is calculated as follows:
, denotes the number of ties to the extent i. The summation term in the numerator is used only if the data series contains tied values. The standard test statistic Zs is calculated as follows:
![]() (8)
(8)
The test statistic Z is used as a measure of significance of trends. In fact, this test statistic is used to test the null hypothesis, H0. If |Zs| is greater than Zα/2, where α represents the chosen significance level (e.g. 5% with Z0.025 = 1.96) then the null hypothesis is invalid implying that the trend is significant. In this study, Mann-Kendall test is used to detect if a trend in rainfall in monthly time series is statistically significant at 99% and 95% levels over the period of 1979-2005.
SEN’s Slope Estimator is used to estimate the gradient of the trends in rainfall [21] . This method provides a more robust slope estimate than the least square method because it is sensitive to the outliers or extreme values. The slope is estimated as follows:
![]() (9)
(9)
where xj and xk are data values at time j and k and j > k correspondingly. The median of these N values of Ti is considered as Sen’s estimator of slope which is given as
![]() (10)
(10)
Sen’s estimator is calculated as ![]() if N is odd, and it is computed as
if N is odd, and it is computed as ![]() if N is even. Lastly Qi is estimated by a two sided test at
if N is even. Lastly Qi is estimated by a two sided test at
100 (1 − α)% confidence interval and then a true slope can be derived by the non-parametric test Qi with a positive value indicates an upward or increasing trend and a negative value of Qi signifies a downward or decreasing trend in the time series. In addition to statistical tests and the trend analysis, the CORDEX RCMs are tested on their ability to reproduce the annual cycles and inter-annual variation of rainfall
3. Results and Discussion
3.1. Rainfall Distribution
Mbaraili River catchment is situated within the semi-arid belt which runs from north to south through the central portion of Tanzania. The mean annual rainfall ranges from 400 mm to 1200 mm. Rainfall increases southwards and on the slopes of the Kipengere range. The seasonal variation of rainfall indicates that the River Catchment experiences a unimodal rainfall regime characterized by a single rainy season extending usually between late November-early December to early-mid May. The eastern portion of the River catchment receives slightly reduced rainfall amounts in February, while the main rainy season peaks in April. The dry season occurs earlier in the central part. The rainfall variability is high, and precipitation is often in the form of heavy showers causing rapid surface runoff and a sudden spate in seasonal streams and rivers [22] .
We first present the spatial rainfall distribution within the Mbarali river catch- ment for the period of 30 years, starting from 1979-2009 (Figure 2). Figure 2 is developed using open source software GrADS (Grid Analysis and Display System) version 2.1.0 (http://cola.gmu.edu/grads/downloads.php). It is clear from the figure that high amount of rainfall (more than 20mm/day) is observed in southern east part of the basin, south-west, and eastern part of the river catchment. However, the central part of the basin and the western part experienced low rainfall amount (16 mm/day).
![]()
Figure 2. Spatial Rainfall distribution (mm/day) over the Mbarali River Catchment.
3.2. Evaluation of RCMs
First, we analyze the available Era Interim Reanalysis data used over Mbarali Ri- ver Catchment for model validation purposes. This was done by purposive sampling of the coordinate points within the catchment. Each coordinate point reproduces rainfall amount at a specified location, and then average all the rainfall data set in order to represent the entire rainfall generated by the ERA-Interim Reanalysis.
Then the second step was to evaluate the regional climate models and their ensemble against the ERA-Interim reanalysis data.
Table 2 represents the RMSE, Mean error and the correlation coefficient between simulated rainfall from the RCMs and rainfall from the ERA-Interim data. CCLM4 model shows the greatest value of RMSE compared to other models. The ensemble mean like most of RCMs exhibits smallest value of RMSE. In the same table, shows relative error with respect to Era Interim over the catchment for the individual RCMs and their ensemble mean.
The RCA4 and HIRHAM5 underestimate rainfall; RACMO and CCLM4 overestimate the reanalysis data values.
Table 2 also shows that the ensemble average of four RCMs performed better in simulating rainfall over Mbarali river catchment compare to the individual RCMs. The correlation coefficient between rainfall data from the ERA Interim and simulated rainfall from the RCMs are also presented in Table 2. It is evident that all the RCMs and the ensemble average are strongly correlated with rainfall from the ERA-interim reanalysis.
The distribution parameters for the mean monthly are shown and compared in Table 3. It is clear that the ensemble average performs better compared to the individual RCMs. The mean, standard deviation and median of the ensemble average are close to those from the ERA interim reanalysis.
The Annual Cycle of Rainfall
Figure 3 present the ability of the RCMs to simulate the annual cycle of rainfall over Mbarali River catchment. It is clear that all the RCMs and the ensemble average reproduce the annual cycles of rainfall over the Mbarali River catchment. However, RCA4 and RACMO overestimate and underestimate seasonal rainfall. Furthermore, the ensemble average performs better in simulating rainfall amount over Mbarali River catchment in all seasons. These findings confirm the earlier results by Luhunga et al. (2016) that the ensemble average can simulate rainfall characteristics better that individual RCMs.
Inter-Annual Variability
The ability of the RCMs to reproduce the inter-annual variation is presented in Figure 4. The data for the RCMs driven by the Era interim reanalysis are available from 1989-2008 and can be accessed through https://esgf-index1.ceda.ac.uk/search/cordex-ceda/. It is evident that all the RCMs and the ensemble average reproduce the inter-annual variation of rainfall over Mbarali River catchment. It can be seen also that the ensemble average reproduces the magnitude of rainfall in the ERA-interim reanalysis compared to the individual RCMs.
![]()
Figure 3. Average annual cycle for precipitation over Mbarali River catchment (calculated from 1971-2005).
![]()
Table 2. Comparison of mean monthly rainfall RCMs in mm and Era interim (1979- 2005).
![]()
Table 3. Distribution parameter. Mean monthly values.
Trends Analysis
The performance of RCM required further examination for their ability to simulate trend in rainfall. The trend of individual model, ensemble RCMs and the Era Interim reanalysis over the Mbarali river catchment are presented in Table 4. It is clear from this table that RCMs forced by GCMs suffers to simulate the trends in rainfall. However, the RCMs forced by ERA-Interim reanalysis data fairly simulate the trends in rainfall. It is important to note that the ensemble average reproduces the trends better than some individual models and some models, for example RCA4 perform better in representing the trends in rainfall than the ensemble average (Table 5).
![]()
Table 4. Mann Kendall trend in rainfall and Sen’s slope estimate in RCMs and Era Interim (calculated for the year 1979-2005).
(*): if trend at α = 0.05 level of significance.
![]()
Table 5. Trends in rainfall, Era driven by all RCMs (calculated for the year 1989-2008).
(**): trend significant at α = 0.01; (*): trend significant at α = 0.05; and (.): trend not significant.
![]()
Figure 4. Annual average RCMs driven by ERA reanalysis, Ensemble RCM, and the Era Interim reanalysis for the Rainfall over Mbarali River catchment.
4. Discussion and Conclusion
In this study, the performance of CORDEX regional climate models in simulating the rainfall characteristics over Mbarali River catchment is presented. The evaluation is based on determining how well the CORDEX RCMs reproduce annual cycles, inter-annual cycles and trends in the rainfall as reproduced by the ERA-Interim reanalysis. It is found that the CORDEX RCMs and the ensemble average reproduce the annual and inter-annual cycles of rainfall over Mbarali River catchment. The ensemble average reproduces better the magnitude and the trends of rainfall compared with the individual models.
Although the CORDEX RCMs and the ensemble average reproduce the annualand inter-annual cycles of rainfall, the models surfer to reproduce correctly the magnitudes of rainfall.
The results of this study will be useful for assessment of climate change impact on stream flow and catchment water balance sensitivity to climate change for the Mbarali River catchment in Rufiji Basin; therefore, it is recommended that for the coming study, the bias correction is essential to be performed to correct the RCMs and their ensemble average for the impact studies.
Acknowledgements
This work was carried out under the Future Climate for Africa UMFULA Project, with the financial. Support from the UK Natural Environment Research Council (NERC), grant ref. No: NE/M020037/1, and the UK Government’s Department for International Development (DfID).
Conflict of Interests
The authors declare that there is no conflict of interest regarding the publication of this paper.