1. Introduction
It is assumed that the Big Bang created equal amounts of matter and antimatter. However, today the Universe consists almost entirely of matter, and what we call ordinary mass is essentially attributed to the effective mass of the valence quarks in protons and neutrons, and to a lesser extent to leptons. As pointed out by Sakharov in 1967 [1] , the early evolution of the Universe must have been controlled by a (chemical) non-equilibrium form of dynamics. Because the density of quarks has increased relative to that of antiquarks [2] . Chemical non equili- brium effects have also been observed in high-energy collisions [3] [4] [5] and been described using the Nambu-Jona-Lasinio model and other effective models [6] - [11] as a starting point for studying the quark-gluon plasma (QGP) and the chiral symmetry breakdown at the QCD phase transition.
As we recently showed in a chemical non-equilibrium derivation [12] of the superconductor-like potential in the electroweak (EW) theory [13] , the surplus of valence quarks probably emerged in a primordial fluctuation before the EW phase transition. Neither in this model, which should also apply to leptons, it was possible to predict the value of the dimensionless coupling to the potential. But as a result of the non-equilibrium conditions, this coupling became a function of the quark (fermion) and antiquark (antifermion) field amplitudes, q and 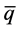 providing a measure of the
providing a measure of the 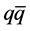 -asymmetry from which the ordinary mass to dark mass ratio could be derived. In this work, we make an attempt to identify dark matter. Unfortunately, in the previous report the term representing dark mass was erroneously lumped together with the infinite number of
-asymmetry from which the ordinary mass to dark mass ratio could be derived. In this work, we make an attempt to identify dark matter. Unfortunately, in the previous report the term representing dark mass was erroneously lumped together with the infinite number of  -pairs in the
-pairs in the 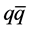 -sea. Instead, the dark mass is expected to be annihilated by its own anti-mass, and obviously the
-sea. Instead, the dark mass is expected to be annihilated by its own anti-mass, and obviously the 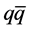 -binding does not become stationary until after the binding is completed. Also, the empirical input-data are modified, but first the model is briefly recapitulated.
-binding does not become stationary until after the binding is completed. Also, the empirical input-data are modified, but first the model is briefly recapitulated.
2. Model
2.1. Rate Equation for Binding of Quarks to Antiquarks
The chemical off-equilibrium conditions are driven by the approximate rate equation
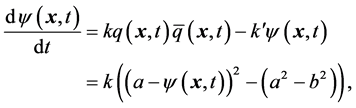 (1)
(1)
for “binding” at a distance of e.g. a massless quark of certain flavor and color to its antiquark, y being the field amplitude of such singlet  -pairs, and k and k' the association and dissociation constants. Insertion of the initial boundary constraints
-pairs, and k and k' the association and dissociation constants. Insertion of the initial boundary constraints  and
and , yields
, yields , where
, where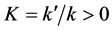 , and
, and , where q0 and
, where q0 and 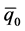 are the initial amplitudes at the Big Bang at which
are the initial amplitudes at the Big Bang at which . All amplitudes are assumed to measure deviations from the corresponding chemical equilibrium quantum fields in a chirality- independent way. Since particles bind to their respective antiparticles when they are approximately at rest relative to each other, initially they exchange only very soft and massless quanta. But k and k' can still depend on relativistic scattering effects. The space coordinate refers to an approximate, fictitious (becoming) centre of mass of the
. All amplitudes are assumed to measure deviations from the corresponding chemical equilibrium quantum fields in a chirality- independent way. Since particles bind to their respective antiparticles when they are approximately at rest relative to each other, initially they exchange only very soft and massless quanta. But k and k' can still depend on relativistic scattering effects. The space coordinate refers to an approximate, fictitious (becoming) centre of mass of the 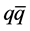 -pairs, and the massless quark and antiquark in such a precursor pair can thus be widely separated and avoid to be promptly annihilated.
-pairs, and the massless quark and antiquark in such a precursor pair can thus be widely separated and avoid to be promptly annihilated.
Equation (1) has the solution
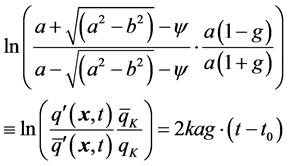 (2)
(2)
where the short-hand notations 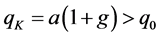 and
and 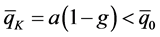 are the screening and screened initial quark and antiquark field amplitudes, and
are the screening and screened initial quark and antiquark field amplitudes, and ![]() is the aforesaid dimensionless coupling that measures the qq̅-asymmetry. The amplitudes
is the aforesaid dimensionless coupling that measures the qq̅-asymmetry. The amplitudes![]() and
and ![]() play the role of new initial boundary constraints, where qK and
play the role of new initial boundary constraints, where qK and ![]() replace q0 and
replace q0 and ![]() as initial amplitudes, as if the pairing started after the fluctuation that gave the quarks a small advantage over the antiquarks,
as initial amplitudes, as if the pairing started after the fluctuation that gave the quarks a small advantage over the antiquarks,![]() . Thus, the number of valence quarks per unit volume has increased from zero to some finite non-zero number. Obviously, this is beyond reach for the grand canonical ensemble, which only allows fluctuations about a constant number of particles in the system [14] .
. Thus, the number of valence quarks per unit volume has increased from zero to some finite non-zero number. Obviously, this is beyond reach for the grand canonical ensemble, which only allows fluctuations about a constant number of particles in the system [14] .
Figure 1 shows schematically how such a dominance of quarks over antiquarks could have emerged from a state with equal amounts of quarks and antiquarks by a fluctuation at the Big Bang. As is clear from Figure 1(a), this asymmetry could not have emerged so easily if there were only a finite number of quarks and antiquarks in the system. In an infinite system, however, the valence quarks and the ![]() -asymmetry can emerge (Figure 1(c)) without compromising the exact pairing (Figure 1(b)) as the temperature decreases.
-asymmetry can emerge (Figure 1(c)) without compromising the exact pairing (Figure 1(b)) as the temperature decreases.
2.2. Spatial Correlations
However, to create a point-like Higgs boson or nucleon, the increasing numbers of becoming ![]() -pairs and valence quarks must be strongly correlated in space. In the actual model this has been accomplished by an infinite discrete lattice [12] , which in the continuum approximation takes the form of a Bose-Einstein distribution [14]
-pairs and valence quarks must be strongly correlated in space. In the actual model this has been accomplished by an infinite discrete lattice [12] , which in the continuum approximation takes the form of a Bose-Einstein distribution [14]
![]() . (3)
. (3)
This distribution corresponds to the grand partition function (GPF), where the factor ![]() is an approximate stationary solution to Equation (1), dys/dt » 0, which like the GPF admits fluctuations. However, in our model the fugacity y/a is driven off chemical equilibrium by Equation (1). The continuum approximation is also key to solve the statistical mechanical problem [12] ,
is an approximate stationary solution to Equation (1), dys/dt » 0, which like the GPF admits fluctuations. However, in our model the fugacity y/a is driven off chemical equilibrium by Equation (1). The continuum approximation is also key to solve the statistical mechanical problem [12] ,
![]()
Figure 1. a) A finite system with equal numbers of quarks and antiquarks is expected to yield just ![]() -pairs. Because if a number of valence quarks were frozen out locally, this should imply a corresponding number of antiquarks at some other place and this has not been observed. b) In an infinite system, however, there are two options: The system can either create only pairs as in the previous case, or alternatively, as in c) One or more valence quarks with baryon number B = 1/3. The remaining still equal amounts of quarks and antiquarks can then produce pairs without leaving any antiquarks behind. The reversed process provides a possible explanation as to how quantum numbers like B are lost, such as in black holes.
-pairs. Because if a number of valence quarks were frozen out locally, this should imply a corresponding number of antiquarks at some other place and this has not been observed. b) In an infinite system, however, there are two options: The system can either create only pairs as in the previous case, or alternatively, as in c) One or more valence quarks with baryon number B = 1/3. The remaining still equal amounts of quarks and antiquarks can then produce pairs without leaving any antiquarks behind. The reversed process provides a possible explanation as to how quantum numbers like B are lost, such as in black holes.
i.e. to describe the dynamics of a system in which the numbers of strongly correlated valence quarks and ![]() -pairs decrease or increase as the temperature increases or decreases.
-pairs decrease or increase as the temperature increases or decreases.
2.3. Derivation of Interaction Potential
The combination of Equation (1) with Equation (3) yields
![]() (4)
(4)
which has the solutions
![]() (5)
(5)
Regarding j(t) as a traveling wave that propagates with velocity k according to
![]() (6)
(6)
we then obtain the potential energy of the system,
![]() (7)
(7)
This has the same form as the double-well potential in the EW theory in the unitary gauge [13] . But by contrast to the standard EW theory, due to the chemical non-equilibrium conditions, the dimensionless coupling parameter, ![]() , has become a function of the quark and antiquark amplitudes that measures the
, has become a function of the quark and antiquark amplitudes that measures the ![]() -asymmetry.
-asymmetry.
After symmetry breakdown, ![]() , the equation of motion reads
, the equation of motion reads
![]() (8)
(8)
where ![]() is identified as the Higgs boson mass mH = 2 ga, and
is identified as the Higgs boson mass mH = 2 ga, and
![]() (9)
(9)
is the translated solution.
It can thus be concluded that both the Higgs boson mass and the valence quark amplitude, ![]() , have grown continuously from zero to the maximum value 2ga as a function of time when the system cools down and the number of
, have grown continuously from zero to the maximum value 2ga as a function of time when the system cools down and the number of ![]() -pairs increases. However, the screening of the underlying gluon field and the concomitant growth of the effective quark masses, are expected to continue until the QCD phase transition.
-pairs increases. However, the screening of the underlying gluon field and the concomitant growth of the effective quark masses, are expected to continue until the QCD phase transition.
3. On Identification of Dark Mass
But if all particles in the infinite lattice of pairs in Equation (3) had a nonzero mass, this would lead to an infinite mass density. The finite Higgs boson mass should therefore correspond to some finite number of massive particles per unit volume. To see how this could occur it is instructive to rewrite ![]() as
as![]() , where the first term
, where the first term![]() , is the valence quark amplitude which corresponds to the ordinary mass density
, is the valence quark amplitude which corresponds to the ordinary mass density ![]() in the Universe. This suggests that the second term,
in the Universe. This suggests that the second term, ![]() , which equals the sum of the non-valence quark amplitude,
, which equals the sum of the non-valence quark amplitude, ![]() , and the antiquark amplitude,
, and the antiquark amplitude, ![]() , could be identified as the amplitude corresponding to dark mass.
, could be identified as the amplitude corresponding to dark mass.
Obviously, the emergence of the finite numbers of the massive valence quarks, and the ![]() -pair components that we associate with dark mass, from the infinite number of massless pairs in the
-pair components that we associate with dark mass, from the infinite number of massless pairs in the ![]() -sea, cannot be described in detail. But a rough picture can be readily obtained by a topological quantization [15] ,
-sea, cannot be described in detail. But a rough picture can be readily obtained by a topological quantization [15] ,![]() , where Nv(t0) and Np(t0) are the numbers of valence quarks and
, where Nv(t0) and Np(t0) are the numbers of valence quarks and ![]() -pairs per unit volume, and mv(t0) and mp(t0) their effective time dependent masses at time 2t0 after Big Bang.
-pairs per unit volume, and mv(t0) and mp(t0) their effective time dependent masses at time 2t0 after Big Bang.
Nv = 0 thus corresponds to a Universe void of nucleons (Figure 1(b)) and Nv ¹ 0 to one containing nucleons and valence quarks (Figure 1(c)). The massive quark-antiquark components of the ![]() -pairs associated with dark masses are assumed to annihilate each other at some finite time after the EW phase transition, implying that
-pairs associated with dark masses are assumed to annihilate each other at some finite time after the EW phase transition, implying that![]() . The valence quarks and the ordinary mass in the Universe could thus be viewed as topological defects that remain after the annihilation of the dark masses in an otherwise empty space. A similar reasoning should hold for leptons and the definition of the Dirac sea. And the same type of relaxation dynamics is assumed to apply to particles that emerge after high-energy proton or heavy-ion collisions.
. The valence quarks and the ordinary mass in the Universe could thus be viewed as topological defects that remain after the annihilation of the dark masses in an otherwise empty space. A similar reasoning should hold for leptons and the definition of the Dirac sea. And the same type of relaxation dynamics is assumed to apply to particles that emerge after high-energy proton or heavy-ion collisions.
The dimensionless parameter l can thus be interpreted as the ratio between the ordinary mass density, and the density of the sum of ordinary and dark masses. The denominator of g, ![]() , equals 348.44 GeV [13] , suggesting that the (indirectly observed) dark mass predominantly consists of the growing mass of a becoming top
, equals 348.44 GeV [13] , suggesting that the (indirectly observed) dark mass predominantly consists of the growing mass of a becoming top ![]() -pair (Np = 1), which then annihilates itself. With mH = 125.09 GeV and j0 = 174.22 GeV we obtain g =125.09/(125.09 + 223.35) = 0.36 and hence l = 0.13, which agrees reasonably well with the ratio l = 0.156 observed [16] [17] . The total dark mass would then become 223.35 GeV, which is a bit higher than expected from observed data [18] .
-pair (Np = 1), which then annihilates itself. With mH = 125.09 GeV and j0 = 174.22 GeV we obtain g =125.09/(125.09 + 223.35) = 0.36 and hence l = 0.13, which agrees reasonably well with the ratio l = 0.156 observed [16] [17] . The total dark mass would then become 223.35 GeV, which is a bit higher than expected from observed data [18] .
But since the quark (and lepton) masses are expected to increase continuously with time, it seems reasonable to assume that the contribution to the observed gravitational effect is due to a time-average of the increasing dark masses. With an observed ratio l = 0.156, this average mass can be estimated to some 85.8% of the value attained at the EW phase transition, l = (125.09)2/(125.09 + 0.858 ´ 223.35)2, which yields a dark mass equal to 0.858 ´ 223.35 = 191.62 GeV. This corresponds approximately to a Higgs boson decaying into two Z bosons and further into two lepton pairs. But 191.62 GeV is also within the limits of the observed excess g-radiation from the Milky Way [18] , corresponding to a Higgs boson that decays into two photons via the “Wilczek vertex” [19] . However, the 191.62 GeV could also correspond to the sum of contributions from all kinds of becoming quark-antiquark and lepton-antilepton pairs [12] . In that case, each of these components may have attained a much smaller mass compared to the Higgs boson mass at the EW phase transition, however, the total dark mass should still amount to about 192 GeV and the top quark and the top antiquark could still be the major contributors to dark matter. The Higgs particle, massive gauge-bosons and photons, and neutrinos too become dark matter candidates in this chemical non-equilibrium extension of the standard model [12] . But it is also a question of abundance of each particle specie. An attempt to estimate the dark energy has been done in the previous work [12] .
4. Emerging Mass versus Newtonian Mass
We have derived a chemical non-equilibrium model in which both the ordinary and dark masses emerge. This contrasts to Newton’s view on mass, who regarded mass as a once and for all given primary quality of matter [19] , which has caused fundamental problems for instance in general relativity (GR); the Schwarzschild metric then acquires singularities both at zero radius and at the Schwarzschild radius in a black hole. In the chemical non-equilibrium model presented here, however, the numbers of valence quarks and ![]() -pairs vanish and thereby their masses when the energy increases. It is probably also what happens in black holes, because the mass density cannot increase towards the central region without simultaneously increasing the energy. Consequently, according to Equation (9) a massive object should become infinitely split into massless quark and lepton pairs as the energy increases and the reaction in Equation (1) goes backward, thereby regularizing the metric in singular regions of black holes [20] .
-pairs vanish and thereby their masses when the energy increases. It is probably also what happens in black holes, because the mass density cannot increase towards the central region without simultaneously increasing the energy. Consequently, according to Equation (9) a massive object should become infinitely split into massless quark and lepton pairs as the energy increases and the reaction in Equation (1) goes backward, thereby regularizing the metric in singular regions of black holes [20] .
This also indicates that the effects on GR and gravitation created by the turmoil from chemical non-equilibrium could be far more important than eventual gravitational quantum effects. Moreover, as a result of the energy increase, the symmetry of the dynamical system is expected to be restored, implying that the decreasing mass of the antiparticles should switch sign [12] . If such a hysteresis type of effect really existed, it would imply a negative form of gravitation, which could provide an explanation for the accelerating expansion of the Universe. As explained in the previous work [12] a Big Bang starting with massless particles could also have a better chance to explain questions about the inflation, than one containing Newtonian type mass already from start and which then explodes.
5. Discussion
Identification of dark matter is expected to be of central importance both for astrophysics and the development of particle physics beyond the standard model. Clearly, this is just a semi-classical model based on rather drastic approximations of a delicate cross-disciplinary problem to describe a dynamical system located in the intersection area between point-like particle physics and condensed matter theory. However, the relaxation dynamics after the Big Bang is more complicated than that, because in order to produce valence quarks, the Universe must have evolved under chemical non-equilibrium conditions, a worst-case scenario in statistical physics. Therefore, the continuum approximation of the strong spatial correlations required to obtain a point-like Higgs boson had to be applied prior to the equilibration at the EW phase transition. This was also key to combine Equation (3) with Equation (1) and to solve the underlying chemical non-equilibrium statistical problem.
At a first sight this may look contradictory, because a point-like particle cannot have structure and condensed matter properties, however, in an approximate sense it can. We started out from a discrete infinite lattice [12] and then made the continuum approximation, in order to be able to accommodate to the chemical non-equilibrium conditions implied by Equation (1) and to the point-likeness of all particles. The non-polynomial scalar field j(t) in Equation (9) then works as a nonlinear mapping between the microscopic subsystem in Equation (3), which contains an infinite number of point-like massless particles, and a “macroscopic” system of some finite number of massive point-like particles that has been frozen out.
Without the solution to this chemical non-equilibrium problem, we could not have obtained the actual relaxation dynamics of the quark-antiquark system that cools down, nor the ![]() -asymmetry, and nor the dark mass term. However, also the stationary state solution
-asymmetry, and nor the dark mass term. However, also the stationary state solution ![]() is approximate, in the sense that dy/dt is small compared to the 100 GeV level. Thus, the equilibrium type EW theory can be expected to work as usual, except that l and j0 in the superconductor-like potential have become functions of the quark (fermion) and antiquark (antifermion) amplitudes. The obtained model and its dark mass candidates can hopefully be tested at the CERN Large Hadron Collider (LHC).
is approximate, in the sense that dy/dt is small compared to the 100 GeV level. Thus, the equilibrium type EW theory can be expected to work as usual, except that l and j0 in the superconductor-like potential have become functions of the quark (fermion) and antiquark (antifermion) amplitudes. The obtained model and its dark mass candidates can hopefully be tested at the CERN Large Hadron Collider (LHC).
In comparison to the QGP energy interval, however, the nonstationary effects become more important and have also been observed [3] [4] [5] [7] [11] . It would therefore be interesting to study the chemical non-equilibrium and spatial correlation effects on QCD and the corresponding effective models, and on the possible role of magnetic monopoles in quark confinement. One could then also hope to gain more information about the properties of QGP near the QCD phase transition, such as the growth of the effective quark masses and hence, indirectly, about the screening of colour gluons [19] [21] . In the linear sigma model, where massive ![]() -pairs play the role of pions and the sigma meson that of a Higgs boson, however, by contrast to the EW transition, the dimensionless coupling has attained a value l > 1 [10] .
-pairs play the role of pions and the sigma meson that of a Higgs boson, however, by contrast to the EW transition, the dimensionless coupling has attained a value l > 1 [10] .
Confinement has also been invoked by employment of a bilinear contact type ![]() -interaction [19] similar to that in Equation (1) with dy/dt = 0. Hopefully, a chemical non-equilibrium extension of such non-perturbative aspects with dy/dt ¹ 0, could then yield information beyond the standard model, not only about the chiral symmetry breakdown and screening of colour gluons, but also a more exact picture of the 85% non-ordinary matter in the Universe.
-interaction [19] similar to that in Equation (1) with dy/dt = 0. Hopefully, a chemical non-equilibrium extension of such non-perturbative aspects with dy/dt ¹ 0, could then yield information beyond the standard model, not only about the chiral symmetry breakdown and screening of colour gluons, but also a more exact picture of the 85% non-ordinary matter in the Universe.
Acknowledgements
I am grateful to Allan Din for providing interesting literature on these subjects.