Modified Function Projective Synchronization of Complex Networks with Multiple Proportional Delays ()
1. Introduction
In recent decades, synchronization as a popular research topic of complex networks has been widespread concern around the world [1] [2] [3] [4] . With the deepening of research on complex networks synchronization problems, the concept and theory of synchronization have been greatly developed, and many different types of synchronization concepts have been found and put forward. such as complete synchronization [5] , cluster synchronization [6] , lag synchro- nization [7] , generalized synchronization [8] , quasi-synchronization [9] , phase synchronization [10] , anti-synchronization [11] , projective synchronization [12] , function projective synchronization [13] [14] .
Modified function projective synchronization(MFPS) has been proposed and extensively investigated in the latest. MFPS means that the drive and response systems could be synchronized up to a desired scaling function matrix [15] . It is easy to see that the definition of MFPS encompasses projective synchronization and function projective synchronization. The MFPS of general complex networks can reveal that the nodes of complex networks could be synchronize up to an equilibrium point or periodic orbit with a desired scaling function matrix. Because the unpredictability of the scaling function in MFPS can additionally enhance the security of communication, MFPS has attracted the interest of many researchers in various fields. On the basis of an adaptive fuzzy nonsingular terminal sliding mode control scheme, a general method of MFPS of two different chaotic systems with unknown functions was investigated in [16] . The work in [17] gives MFPS of a class of chaotic systems. MFPS of a classic chaotic systems with unknown disturbances was investigated by adaptive integral sliding mode control [18] . Ref. [19] investigates the adaptive MFPS of a class of complex four-dimensional chaotic system with one cubic cross-product term in each equation. Ref. [20] investigates the MFPS of two different chaotic systems with parameter perturbations.
A simple general scheme of MFPS in complex dynamical networks (CDNs) is investigated in this paper, considering that external disturbances and unmodeled dynamics are always unavoidably in the practical evolutionary processes of synchronization, MFPS in CDNs with proportional delay and disturbances will be investigated by the proposed scheme.The rest of this paper is organized as follows. Some definitions and a basic lemma are given in Section 2. In Section 3, the synchronization of the complex networks with proportional delays by the pinning control method is discussed by the way of equivalent system. Finally, computer simulation is performed to illustrate the validity of the proposed method in Section 4.
2. Preliminaries
Consider a generally controlled complex dynamical networks consisting of N identical linearly coupled nodes with multiple proportional delays by the following equations:
(2.1)
where
denotes the state vector of the ith node,
is a continuously differentiable vector function determining the dynamic behavior of the nodes,
is the control input.
is the coupling configuration matrix representing the topolo- gical structure of the network, where
if there is a connection between node i and node j; otherwise
, and the diagonal elements of matrix
are defined by
(2.2)
are proportional delay factors and satisfy
. Furthermore, the complex network described in (2.1) possess initial conditions of
,
are constants.
Definition 1. (MFPS) The network (2.1) with proportional delays is said to achieve modified function projective synchronization if there exists a continu- ously differentiable scaling function matrix
such that
(2.3)
where
stands for the Euclidean vector norm,
is a modified function matrix, and each modified function
is a continuously differential function and is bounded as
,
,
is a finite constant, and
can be an equilibrium point, or a periodic orbit, or an orbit of a chaotic attractor, which satisfies
.
Considering the actual evolutionary processes of synchronization, external disturbances and unmodeled dynamics are always unavoidable. MFPS in CDNs with disturbances will be investigated further as follows:
#Math_26# (2.4)
where
denotes the state vector of the ith node,
is a continuously differentiable vector function determining the dynamic behavior of the nodes,
is the control input and
is the mismatched terms, which could exist in many perturbation, noise disturbance.
is the coupling configuration matrix represent- ing the topological structure of the network, and the diagonal elements of matrix
are defined by Equation (2.2).
In the following, some necessary assumptions are given.
Assumption 1. The derivative of scaling function
is bounded, that is
(2.5)
for all
, where
is the upper limit of the
.
Assumption 2. The norm of the mismatched terms
are bounded, that is
(2.6)
where
is the upper limit of the norm of
.
In this paper,
denote the upper limit of the norm of
,
, respectively.
,
represent the Kroncecker product,
denotes the maximum eigenvalue for symmetric matrix
.
Lemma 1. [21] For any vector
and positive definite matrix
, the following matrix inequality holds:
(2.7)
3. MFPS in Complex Networks with Multiple Proportional Delays
In this section, a hybrid feedback control method for realizing modified function projective synchronization in complex dynamical networks with multiple proportional delays is proposed.
Let
, then a couple of networks (2.1) and (2.4) is equivalently transformed into the following couple of complex networks with constant delay and time varying coefficients
(3.1)
and
#Math_54# (3.2)
where
,
,
, and
, in which
,
.
Definition 2. The network (3.2) is said to achieve modified function projec- tive synchronization if there exists a continuously differentiable scaling function matrix
such that
(3.3)
where
stands for the Euclidean vector norm,
is a modified function matrix, and each modified function
is a continuously differential function and is bounded as
,
,
is a finite constant, and
can be an equilibrium point, or a periodic orbit, or an orbit of a chaotic attractor, which satisfies
.
Theorem 1. Suppose Assumptions 1 and 2 hold. For a given synchronization scaling function matrix
, if there exist positive constants
,
and
which satisfy
,
and
, CDNs
with disturbance (3.2) can realize modified function projective synchronization via the control law :
#Math_78# (3.4)
where
denotes the sign function.
Proof. Define
(3.5)
where
is a modified function matrix. It follows from (3.2) and (2.2) that
(3.6)
Construct the Lyapunov function
(3.7)
The time derivative of V(t) along the trajectories of system (3.6) is
 (3.8)
(3.8)
Because chaos systems and the scaling function are bounded,
and
are bounded. Furthermore,
is a continuously vector function, there exists a positive constants
satisfying
. Because Assumption 1 holds, there exists a positive constant
satisfying
. Because Assumption 2 holds, there exists a positive constant
satisfying
:
(3.9)
Tanking
and
,
, we obtain
(3.10)
where
.
Let
. Then by Lemma 1, we have
(3.11)
Taking
, we obtain
(3.12)
According to the Lyapunov stability theory, the error system (3.6) is asymptotically stable. This completes the proof.
Corollary 1. Suppose Assumptions 1 hold. For a given synchronization scaling function matrix
, if there exist positive constants
,
,
,
which satisfy
,
and
, CDNs without
disturbance (3.1) can realize modified function projective synchronization via the control law :
#Math_111# (3.13)
where
denotes the sign function.
By Theorem 1, it is easy to see that a similar proof holds for
. Thus, the proof is omitted here.
Though the proposed error feedback control method is very simple, Choosing the appropriate feedback gains
,
and
is still difficult. Thus, finding appropriate gains
,
and
to achieve synchronization is still a challenging problem. In the following, an adaptive scheme is established in order to select the appropriate gains
,
and
to realize MFPS in CDNs with or without disturbances.
Theorem 2. Suppose Assumptions 1 and 2 hold. For a given synchronization scaling function matrix
, CDNs with disturbance (3.2) can realize modified function projective synchronization via the control law :
(3.14)
(3.15)
(3.16)
(3.17)
where
denotes the sign function.
and
are arbi- trary positive constants. Proof. Construct the Lyapunov function
(3.18)
The time derivative of V(t) along the trajectories of (3.6) is
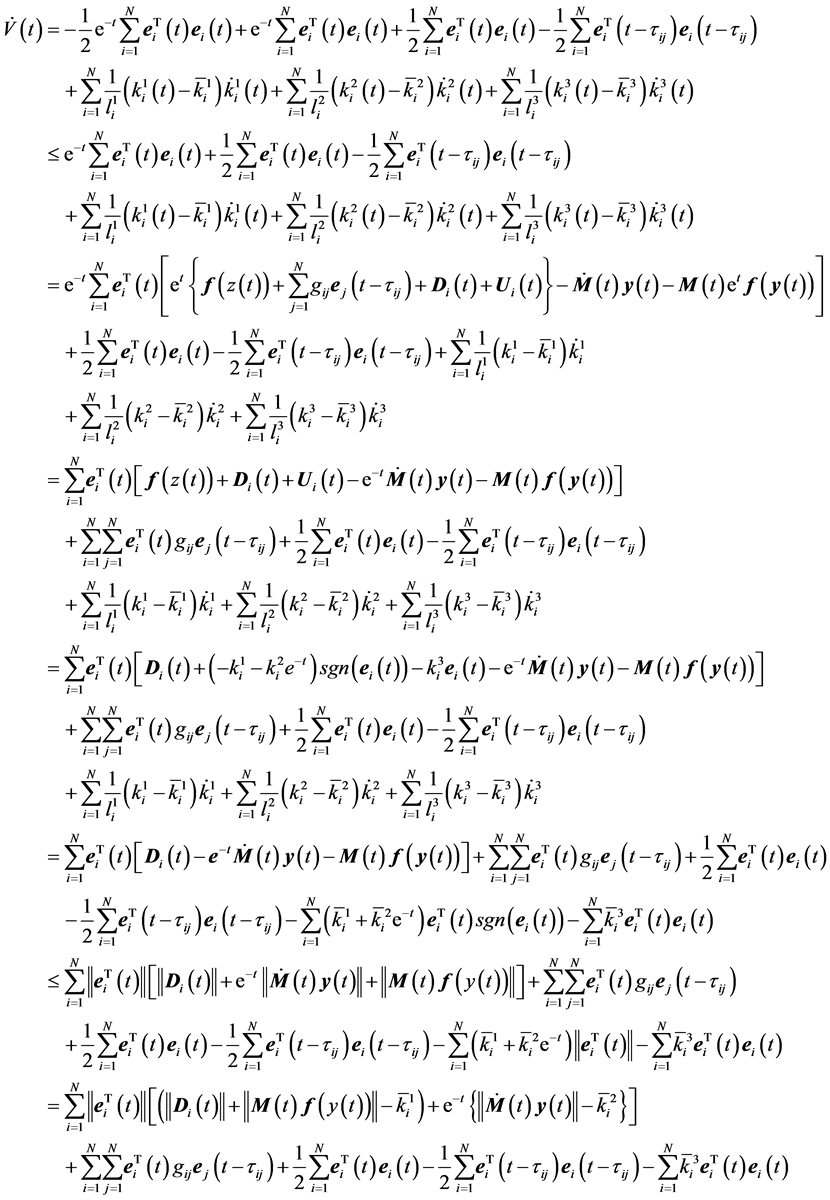 (3.19)
(3.19)
Because chaos systems and the scaling function are bounded,
and
are bounded. Furthermore,
is a continuously vector function, there exists a positive constants
satisfying
. Because As- sumption 1 holds, there exists a positive constant
satisfying
. Because Assumption 2 holds, there exists a positive constant
satisfying
:
(3.20)
Tanking
and
,
, we obtain
(3.21)
where
.
Let
. Then by Lemma 1, we have
(3.22)
Taking
, we obtain
(3.23)
According to the Lyapunov stability theory, the error system (3.6) is asymptotically stable. This completes the proof.
Corollary 2. Suppose Assumptions 1 hold. For a given synchronization scaling function matrix
, CDNs without disturbance (3.1) can realize modified function projective synchronization via the control law (3.14)-(3.17).
By Theorem 2, it is easy to see that a similar proof holds for
. Thus, the proof is omitted here.
4. Computer Simulation
In this section, the chaotic Lorenz system is taken as nodes of CDNs to verify the effectiveness of the proposed scheme in Corollary 2.
Consider the following single Lorenz system:
(4.1)
where
. Figure 1 and Figure 2 depict the chaotic attractor
and components of the Lorenz system respectively. The coupling configuration matrix
is chosen to be
![]()
Figure 1. Chaotic attractor of the Lorenz system.
![]()
Figure 2. Components of the Lorenz system.
Complex networks with proportional delays can be described as follows:
(4.2)
where the controllers
satisfied:
,
can be designed by using Theorem 2 as follows:
with
where
,
,
In this numerical simulation, we take the initial states as
,
,
,
. We take
,
,
,
,
,
,
,
,
,
and
. The numerical results are
presented in Figure 3 and Figure 4. Figure 3 displays the state phases of the Lorenz system. The time evolution of the synchronization errors is depicted in Figure 4, which displays
with
. These results show that function projective synchronization takes place with the desired scaling function in complex networks (4.2).
5. Concluding Remarks
In this paper, function projective synchronization schemes for complex net- works with proportional delays are given by a error feedback control method. Numerical simulation is provided to show the effectiveness of our result.
![]()
Figure 3. State phases of the Lorenz system.
![]()
Figure 4. The time evolution of the synchronization errors e.
Acknowledgements
This work is jointly supported by the Natural Science Foundation of China (11101187, 61573005, 11361010), the Scientific Research Fund of Fujian Provincial Education Department of China (JAT160691).