Error Estimations, Error Computations, and Convergence Rates in FEM for BVPs ()
Received 3 June 2016; accepted 26 July 2016; published 29 July 2016

1. Introduction
It is now well recognized that in finite element computations there are three independent parameters: characteristic length of the discretization h, degree of approximation p, and the order k of the scalar product space. h and p have been well known for quite some time but introduction of k as an additional independent parameter in finite element computations is rather recent. Surana et al. [1] - [4] have shown the order k of the approximation space to be an independent parameter in all finite element computational processes in addition to h and p, hence k-version of finite element method in addition to h- and p-versions. The order k of the approximation space ensures global differentiability of order  over the whole discretization. The appropriate choice of k is essential in ensuring that 1) the desired physics is preserved in the computational process and 2) the integrals are Riemann in the entire finite element process so that the equivalence of BVP with the integral form is preserved and the errors in the calculated solution can be computed correctly without knowledge of the theoretical solution. We elaborate more on some of these aspects in the following.
over the whole discretization. The appropriate choice of k is essential in ensuring that 1) the desired physics is preserved in the computational process and 2) the integrals are Riemann in the entire finite element process so that the equivalence of BVP with the integral form is preserved and the errors in the calculated solution can be computed correctly without knowledge of the theoretical solution. We elaborate more on some of these aspects in the following.
If the differential operator contains highest order derivatives of the dependent variables of orders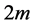 , then the approximation of the solutions of the BVP must at least be of class
, then the approximation of the solutions of the BVP must at least be of class  i.e. of global differentiability of order
i.e. of global differentiability of order 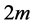 in order for this approximation to be admissible in the BVP in the pointwise sense. This requires that the order k of the approximation space must at least be
in order for this approximation to be admissible in the BVP in the pointwise sense. This requires that the order k of the approximation space must at least be 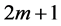 i.e.
i.e. 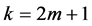 is minimally conforming order of the approximation space. Clearly, the order k of the minimally conforming space is determined by the highest order of the derivatives of the dependent variable(s) in the BVP. When
is minimally conforming order of the approximation space. Clearly, the order k of the minimally conforming space is determined by the highest order of the derivatives of the dependent variable(s) in the BVP. When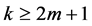 , all integrals over the discretization
, all integrals over the discretization 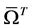 remain Riemann. When
remain Riemann. When , the integrals over
, the integrals over 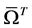 are in Lebesgue sense and the corresponding approximation
are in Lebesgue sense and the corresponding approximation 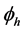 of the solution
of the solution 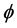 over
over 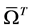 is not admissible in the BVP
is not admissible in the BVP  in the pointwise sense. When
in the pointwise sense. When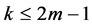 , the approximation
, the approximation ![]() of
of ![]() over
over ![]() is not admissible at all in the BVP. Choosing
is not admissible at all in the BVP. Choosing ![]() may be beneficial if the theoretical solution
may be beneficial if the theoretical solution ![]() of the BVP is of higher order global differentiability than 2m as this choice incorporates higher order global differentiability aspects of
of the BVP is of higher order global differentiability than 2m as this choice incorporates higher order global differentiability aspects of ![]() in the computational process. Thus, now we have h-, p-, k-versions of the finite element processes and associated convergences and convergence rates.
in the computational process. Thus, now we have h-, p-, k-versions of the finite element processes and associated convergences and convergence rates.
The subject of a priori error estimation and a posteriori error estimation have been exhaustively studied and investigated with the objective that 1) perhaps a priori error estimates will help us in deciding the most prudent choices of h, p, and k so that the errors in the desired norms are reduced at the fastest rate during computations, 2) the a posteriori error estimates will guide us based on the current finite element solution in improving the accuracy of the subsequently computed solutions in the most prudent manner. The published literature on this subject is enormous and discussion of each writing on the subject in this paper is not feasible and is also of little benefit. Interested readers can refer to some selected publications [5] - [34] included here.
In the work presented in this paper, our objectives are:
a) To derive a priori error estimates for BVPs described by self adjoint, non-self adjoint, and nonlinear differential orperators when the theoretical solutions are analytic, thus establishing precise dependence of the chosen error norm on h, p, k, and the smoothness of the theoretical solution (for simplicity this is done using one dimensional BVPs).
b) To discuss the currently used a posteriori error estimation techniques, their shortcomings, and serious inadequacies when actual physics of the BVP is incorporated in the finite element computational process.
c) To demonstrate the need for a posteriori error computation and present a framework in which those computations can be performed without the knowledge of theoretical solutions.
d) To establish that higher order approximation spaces and variationally consistent integral forms are essential for incorporating the desired physics of the BVP in the computational process and to ensure that the resulting finite element computational processes are unconditionally stable so that error estimations remain meaningful.
e) To perform numerical studies using one dimensional boundary value problem described by self adjoint, non-self adjoint, and nonlinear differential operators and to demonstrate exceptionally good agreement of the computed convergence rates with those established theoretically.
f) To establish that the a priori error estimates derived in (a) also hold for 2D and 3D BVPs when the integral forms in those BVPs are variationally consistent.
2. Preliminaries: Convergence and Convergence Rates, Convergence Behavior of Computations, Error Estimation, and Error Computations
In this section, we present some preliminary material and concepts that are essential in error estimation and error computations. Many of these are well known but are included in the following for completeness and for the sake of coherent continuation to the new work in this paper.
2.1. Convergence and Convergence Rate
Convergence of a finite element solution implies behavior of the error in the finite element solution (measured in some norm) as a function of the degrees of freedom or the characteristic length of the discretization. When the theoretical solution is known, the error in the finite element solution in some norm (L2-norm, H1-norm, etc.) can be computed and therefore we can study its behavior as a function of the degrees of freedom. When the theoretical solution is not known, perhaps estimating the error in some norm in the computed solution is a viable option. However, we shall see in a later section that this option only works in a restricted range of the behavior of error norm versus dofs. The third option is that if we are using minimally conforming spaces ![]() then residual functional
then residual functional ![]() can be computed precisely as for minimally conforming spaces all integrals over the discretization
can be computed precisely as for minimally conforming spaces all integrals over the discretization ![]() of
of![]() , the domain of definition of the BVP, are Riemann. Proximity of
, the domain of definition of the BVP, are Riemann. Proximity of ![]() to zero is a measure of error due to the fact that when
to zero is a measure of error due to the fact that when![]() ,
,![]() . Thus,
. Thus, ![]() is in fact error measure in the solution
is in fact error measure in the solution ![]() over
over![]() . This option can always be used for any applications as it does not require theoretical solution but necessitates the approximation
. This option can always be used for any applications as it does not require theoretical solution but necessitates the approximation ![]() to be in a space of order
to be in a space of order![]() . In what follows we can use
. In what follows we can use ![]() as a measure of error over
as a measure of error over![]() , hence convergence of the computed solution
, hence convergence of the computed solution ![]() to
to ![]() implies studying
implies studying ![]() versus dofs as more degrees of freedom are added to the discretization. When
versus dofs as more degrees of freedom are added to the discretization. When![]() , a predetermined tolerance of computed zero, we consider the finite element solution
, a predetermined tolerance of computed zero, we consider the finite element solution ![]() to be converged to the
to be converged to the
theoretical solution![]() . We consider
. We consider ![]() versus dofs or
versus dofs or![]() , L2-norm of residual E.
, L2-norm of residual E.
We study ![]() versus dofs using log-log scale, or more precisely we study
versus dofs using log-log scale, or more precisely we study ![]() versus log(dofs).
versus log(dofs). ![]() and log(dofs) or log-log scale are necessary as the range of I could be
and log(dofs) or log-log scale are necessary as the range of I could be ![]() -
- ![]() and the range of dof could be
and the range of dof could be ![]() -
-![]() or higher.
or higher.
2.2. Convergence Behavior of Computations
The material presented in this section is based on ![]() versus dof behavior, but the same concepts hold true for any other measure of error norm (i.e.
versus dof behavior, but the same concepts hold true for any other measure of error norm (i.e. ![]() can be replaced with any other error norm without affecting the basic behavior of the convergence graph). A typical convergence behavior of
can be replaced with any other error norm without affecting the basic behavior of the convergence graph). A typical convergence behavior of ![]() or
or ![]() versus log(dof) is shown in Figure 1. This graph is generated using 1D convection-diffusion equation (a second order ODE) with
versus log(dof) is shown in Figure 1. This graph is generated using 1D convection-diffusion equation (a second order ODE) with ![]() and least squares finite element formulation based on residual functional. The progressively graded discretizations are generated beginning with two elements using a constant geometric ratio of 1.5. The smallest element is located at
and least squares finite element formulation based on residual functional. The progressively graded discretizations are generated beginning with two elements using a constant geometric ratio of 1.5. The smallest element is located at![]() .
. ![]() is used as it corresponds to the minimally conforming space. Minimum p-level of 5 (needed for
is used as it corresponds to the minimally conforming space. Minimum p-level of 5 (needed for![]() ) is considered for each progressively refined discretization. From Figure 1, we observe five distinct zones. In each one of these zones the behavior of
) is considered for each progressively refined discretization. From Figure 1, we observe five distinct zones. In each one of these zones the behavior of ![]() versus dofs is unique and distinct. The behavior of
versus dofs is unique and distinct. The behavior of ![]() versus log(dofs) shown in Figure 1 illustrates the varying rate of convergence of the finite element solution (the slope of the curve) with varying dofs. In the middle portion represented by almost a straight line behavior the slope is almost constant, indicating constant convergence rate. We discuss the details related to the varying slope of the curve, associated rate of convergence, and its significance in the following.
versus log(dofs) shown in Figure 1 illustrates the varying rate of convergence of the finite element solution (the slope of the curve) with varying dofs. In the middle portion represented by almost a straight line behavior the slope is almost constant, indicating constant convergence rate. We discuss the details related to the varying slope of the curve, associated rate of convergence, and its significance in the following.
![]()
Figure 1. Typical convergence behavior of a finite element solution.
Pre-asymptotic range (AB): The range AB is called pre-asymptotic range. In this range as we move from location A toward location B additional degrees of freedom are added to the discretization but there is virtually no measurable reduction in the L2-norm of E. The accuracy of the computed solution in this range is very poor (due to ![]() of the
of the![]() ). Due to poor accuracy of the solution
). Due to poor accuracy of the solution![]() , hence
, hence![]() , the
, the ![]() values for the elements are poor as well, hence these cannot be used to guide any form of adaptive refinement process. A posteriori error estimations in this range are not possible either as these require some regularity in the computed solution which is absent in
values for the elements are poor as well, hence these cannot be used to guide any form of adaptive refinement process. A posteriori error estimations in this range are not possible either as these require some regularity in the computed solution which is absent in ![]() in range AB. Thus, in this range adaptive processes are not possible as reliable indicators (either estimated or computed) based on
in range AB. Thus, in this range adaptive processes are not possible as reliable indicators (either estimated or computed) based on ![]() are not possible.
are not possible.
Onset of asymptotic range (BC): The range BC is called onset of asymptotic range. In this range addition of degrees of freedom to the discretization results in measurable reduction in ![]() reflecting progressive improvement in accuracy of the computed solution
reflecting progressive improvement in accuracy of the computed solution ![]() from B to C. In this range
from B to C. In this range ![]() values or any other possible element error indicators are more accurate than range AB. In this range adaptive processes in h, p, or hp can be utilized keeping in mind that as we move closer to C, the values of
values or any other possible element error indicators are more accurate than range AB. In this range adaptive processes in h, p, or hp can be utilized keeping in mind that as we move closer to C, the values of ![]() (or other indicators) for the elements of the discretization become more accurate, hence can be more effective in the adaptive process.
(or other indicators) for the elements of the discretization become more accurate, hence can be more effective in the adaptive process.
Asymptotic range (CD): In this range as more dofs are added to the discretization the improvement (reduction) in ![]() is most significant. This range on log-log scale is nearly linear, hence constant slope. Adaptive refinements in this range are most effective in reducing
is most significant. This range on log-log scale is nearly linear, hence constant slope. Adaptive refinements in this range are most effective in reducing![]() . We observe that between C and D there are several orders of magnitude reduction in the value of
. We observe that between C and D there are several orders of magnitude reduction in the value of![]() . Slope of the error norm versus dof graph in this range is called the asymptotic convergence rate of the finite element solution.
. Slope of the error norm versus dof graph in this range is called the asymptotic convergence rate of the finite element solution.
Onset of post-asymptotic range (DE): This range is almost reverse of the onset of asymptotic range. In this range reduction in ![]() progressively diminishes with the addition of degrees of freedom to the discretization indicating that substantial achievable reduction in
progressively diminishes with the addition of degrees of freedom to the discretization indicating that substantial achievable reduction in ![]() has taken place up to point D. Computations in this range result in waste of significant resources (dofs) with very little gain in the objective of reducing
has taken place up to point D. Computations in this range result in waste of significant resources (dofs) with very little gain in the objective of reducing![]() .
.
Post-asymptotic range (EF): In this range in spite of the addition of dofs to the discretization no measurable reduction is observed in![]() . This is generally due to the fact that within the accuracy of the computations (i.e. the word size on the computer we have reached a limit), hence the accuracy remains limited to the same number of decimal places in
. This is generally due to the fact that within the accuracy of the computations (i.e. the word size on the computer we have reached a limit), hence the accuracy remains limited to the same number of decimal places in ![]() regardless of the increase in dofs.
regardless of the increase in dofs.
2.3. Convergence Rates
In range AB, the slope is almost zero. From B to C the slope increases as more dofs are added to the discretization thereby progressively increasing convergence rate from B to C. From C to D, the asymptotic range, the slope of ![]() versus dofs is almost constant and the reduction in
versus dofs is almost constant and the reduction in ![]() is most significant as more dofs are added. Thus, in the asymptotic range the convergence rate is the highest (due to highest slope of
is most significant as more dofs are added. Thus, in the asymptotic range the convergence rate is the highest (due to highest slope of ![]() versus log(dof)) and is constant. In the onset of post-asymptotic range DE the convergence rate decreases and eventually becomes almost zero in the post-asymptotic range EF.
versus log(dof)) and is constant. In the onset of post-asymptotic range DE the convergence rate decreases and eventually becomes almost zero in the post-asymptotic range EF.
Remarks
I) Behavior of ![]() versus dofs shown in Figure 1 is typical of other error norms as well, hence the discussion and conclusions related to Figure 1 are applicable in the convergence behavior study using any other desired error norm.
versus dofs shown in Figure 1 is typical of other error norms as well, hence the discussion and conclusions related to Figure 1 are applicable in the convergence behavior study using any other desired error norm.
II) Pre-asymptotic range AB, onset of post-asymptotic range DE, and post-asymptotic range EF should be avoided as in these ranges solution accuracy improvement is poor.
III) In range AB ![]() values (or other measures) are not accurate enough to guide an adaptive process of any kind.
values (or other measures) are not accurate enough to guide an adaptive process of any kind.
IV) Adaptive processes (![]() ) can be initiated in the range BC as
) can be initiated in the range BC as ![]() values in this range are reasonable measure of error. Adaptive processes become more and more effective when we initiate them as we approach from B to C. In the range BC the slope of
values in this range are reasonable measure of error. Adaptive processes become more and more effective when we initiate them as we approach from B to C. In the range BC the slope of ![]() versus dof increases from B to C indicating improving convergence rate and eventually achieves the highest convergence rate value at C which remains almost constant in the asymptotic range CD.
versus dof increases from B to C indicating improving convergence rate and eventually achieves the highest convergence rate value at C which remains almost constant in the asymptotic range CD.
V) A priori and a posteriori error estimates are only valid in the asymptotic range due to the fact it is only in this range that computed ![]() has desired regularity and the convergence rate is the highest, hence worth estimating a priori. The error estimates (a priori and a posteriori) can neither be derived accurately nor can be used meaningfully in regions other than BC.
has desired regularity and the convergence rate is the highest, hence worth estimating a priori. The error estimates (a priori and a posteriori) can neither be derived accurately nor can be used meaningfully in regions other than BC.
2.4. Error Estimation and Error Computation
There are two types of error estimations generally considered: a priori error estimation and a posteriori error estimation. A priori error estimation refers to establishing dependence of some error norm on h, p, k, and the regularity of the theoretical solution before the computations are performed so that we have knowledge of the precise nature of the functional dependence of error norm on h, p, k, and the regularity of the theoretical solution. A posteriori error estimation refers to error estimates derived using a computed solution with specific choices of h, p, and k. The sole purpose of a posteriori error estimation is to use current finite element solution to derive element indicators that can perhaps be used to guide an adaptive process. Both of the error estimations require some regularity of the computed solution which only exists in the asymptotic range (range CD, Figure 1). This is a very significant restriction on the use of these estimates. For example, a priori error estimate cannot be used to predict convergence rate in the ranges AB, BC, DE, and EF as this is specifically derived using the regularity of ![]() that only exists in the asymptotic range. Likewise a posteriori estimate cannot be used for adaptivity in any ranges except CD.
that only exists in the asymptotic range. Likewise a posteriori estimate cannot be used for adaptivity in any ranges except CD.
Another point to note is that a posteriori error estimates are generally derived such that they quantify the
weakness (es) in the finite element global approximation![]() . Their derivations are largely based on
. Their derivations are largely based on ![]()
local approximations which result in interelement discontinuity of the derivatives normal to the interelement boundaries. This may be quantified by establishing bounds that can be used for adaptivity. However if we use ![]() of class
of class ![]() thereby
thereby ![]() of class
of class![]() , then such bounds are meaningless. In k-version of finite element methods enabling higher order global differentiability approximations, majority of the a posteriori error estimates based on interelement discontinuity of the derivatives are not meaningful. With the use of higher order approximations
, then such bounds are meaningless. In k-version of finite element methods enabling higher order global differentiability approximations, majority of the a posteriori error estimates based on interelement discontinuity of the derivatives are not meaningful. With the use of higher order approximations![]() , the integrals can be maintained Riemann,
, the integrals can be maintained Riemann, ![]() and
and ![]() are true measures of the error in the finite element solution for
are true measures of the error in the finite element solution for ![]() and
and ![]() and can indeed be used in adaptive processes. These aspects are discussed in more details in later sections.
and can indeed be used in adaptive processes. These aspects are discussed in more details in later sections.
3. Variationally Consistent (VC) and Variationally Inconsistent (VIC) Integral Forms
The differential operators appearing in the totality of all BVPs can be mathematically classified in three categories: self-adjoint, non-self-adjoint, and nonlinear differential operators. The finite element processes for these operators can be derived by constructing integral forms using methods of approximation such as: Galerkin method (GM), Petrov-Galerkin method (PGM), weighted residual method (WRM), Galerkin method with weak form (GM/WF), and least squares method or process (LSP). The unconditional stability of the resulting computational process or lack thereof can be established by making a correspondence of these integral forms to the elements of the calculus of variations [1] - [4] [35] . The integral forms that result in unconditionally stable computational processes are termed variationally consistent (VC). The others are called variationally inconsistent (VIC). In VC integral forms the assembled coefficient matrices always remain positive-definite regardless of the admissible choices of h, p, and k whereas in VIC integral forms this can not always be ensured.
Definition 3.1 (consistent (VC) integral form of a BVP) A variationally consistent integral form corresponding to the BVP ![]() consists of
consists of
1) Existence of a functional ![]() corresponding to the BVP
corresponding to the BVP![]() . This is generally by construction (or is assumed).
. This is generally by construction (or is assumed).
2) Necessary condition for the existence of an extremum of ![]() is given by
is given by![]() . The integral form
. The integral form ![]() is used to determine
is used to determine![]() . The Euler’s equation resulting from
. The Euler’s equation resulting from ![]() must be the BVP
must be the BVP![]() .
.
3)![]() ,
, ![]() ,
, ![]() (minimum, saddle point, maximum of
(minimum, saddle point, maximum of![]() ) is the sufficient condition or extremum principle. Extremum principle ensures that a
) is the sufficient condition or extremum principle. Extremum principle ensures that a ![]() obtained from
obtained from ![]() is unique. Extremum principle also establishes whether
is unique. Extremum principle also establishes whether ![]() from
from ![]() minimizes or maximizes
minimizes or maximizes ![]() or yields a saddle point of
or yields a saddle point of![]() .
.
When all these three elements are present in an integral formulation of the BVP![]() , then the integral form (resulting from
, then the integral form (resulting from ![]() or otherwise) is called a variationally consistent integral form of the BVP
or otherwise) is called a variationally consistent integral form of the BVP ![]() (or simply VC integral process). VC integral form or process yields unique extremum of the functional
(or simply VC integral process). VC integral form or process yields unique extremum of the functional ![]() corresponding to
corresponding to![]() , hence a unique solution of the BVP
, hence a unique solution of the BVP ![]() (the Euler’s equation resulting from
(the Euler’s equation resulting from![]() ).
).
Definition 3.2 (inconsistent integral form (VIC) of a BVP) If an integral form of a BVP (resulting from ![]() or otherwise) is not variationally consistent, then it is variationally inconsistent. A variationally inconsistent integral form or process violates one or more of the three requirements needed for variational con- sistency of the integral form.
or otherwise) is not variationally consistent, then it is variationally inconsistent. A variationally inconsistent integral form or process violates one or more of the three requirements needed for variational con- sistency of the integral form.
Remarks
1) Thus, we see that a variationally consistent integral form of a BVP ![]() emerges as a method of obtaining a unique solution of the BVP
emerges as a method of obtaining a unique solution of the BVP![]() .
.
2) The necessary condition (the integral form resulting from ![]() or otherwise) provides a system of algebraic equations from which the solution
or otherwise) provides a system of algebraic equations from which the solution ![]() is determined.
is determined.
3) The sufficient condition or unique extremum principle ensures that a ![]() obtained from the integral form (
obtained from the integral form (![]() or otherwise) is unique, hence this
or otherwise) is unique, hence this ![]() yields a unique extremum of
yields a unique extremum of ![]() as well as a unique solution of the Euler’s equation which is the BVP under consideration.
as well as a unique solution of the Euler’s equation which is the BVP under consideration.
4) Variationally consistent integral forms yield symmetric coefficient matrices in the algebraic systems and the coefficient matrices are positive-definite, hence have real, positive eigenvalues and real eigenvectors (basis). Such coefficient matrices are invertible, hence yield unique values of the unknowns in the corresponding algebraic systems.
5) When the integral form is variationally inconsistent, a unique extremum principle does not exist. In such cases the coefficient matrix in the algebraic system resulting from the integral form is not symmetric, hence is not ensured to be positive-definite. A unique solution of the unknowns in such algebraic systems is not ensured. A consequence of the non-positive-definite coefficient matrix in the algebraic system is that such coefficient matrices may have zero or negative eigenvalues or the eigenvalues and eigenvectors may be complex. In summary, variationally inconsistent integral forms must be avoided at all cost due to the fact that when using such integral forms a unique solution of the BVP is not ensured. In other words when obtaining solution of BVPs, variationally consistent integral forms are essential to ensure unique solutions of the BVPs.
6) The definition stated above can be applied to any BVP provided we can show existence of a functional ![]() corresponding to the BVP
corresponding to the BVP ![]() such that
such that ![]() and
and ![]() are necessary and sufficient conditions for the existence of extremum of
are necessary and sufficient conditions for the existence of extremum of![]() . A
. A ![]() yielding unique extremum of
yielding unique extremum of ![]() is also a unique solution of
is also a unique solution of![]() .
.
7) We can show (see ref. [1] - [4] [35] for details) that a) the integral forms resulting from GM/WF are VC only for self-adjoint differential operators when the bilinear functional is symmetric, b) the integral form resulting from LSP is VC for all three classes of differential operators, and c) integral forms resulting from the other methods of approximation (GM, PGM, WRM) for all three clases of differential operators are VIC.
8) We show that VC integral forms in designing finite element processes are essential for the derivations of the a priori error estimates.
9) In the following, we only consider GM/WF and LSP, keeping in mind that the integral form from GM/WF is VC only for self-adjoint differential operators and for LSP the integral forms are VC for all three classes of operators.
4. Variational Consistency of the Integral Form and the Best Approximation Property
In this section, we present some theorems and their proofs regarding GM/WF and LSP for the three classes of differential operators and establish best approximation property of GM/WF for self-adjoint operators and LSP for all three classes of operators.
4.1. Galerkin Method with Weak Form (GM/WF): Self-Adjoint Operators
In this section, we revisit main steps of GM/WF for self-adjoint operators. Let
![]() (1)
(1)
be a boundary value problem in which the differential operator A is symmetric and its adjoint ![]() (i.e. the differential operator A is self adjoint). Based on fundamental lemma of calculus of variations we can write the following integral form [1] [35] :
(i.e. the differential operator A is self adjoint). Based on fundamental lemma of calculus of variations we can write the following integral form [1] [35] :
![]() (2)
(2)
in which ![]() on
on ![]() if
if ![]() (given) on
(given) on![]() . v is called test function, hence
. v is called test function, hence ![]() is admissible in (2). When
is admissible in (2). When ![]() in (2), the integral form (2) is called integral form in Galerkin method. Since A is self adjoint, the BVP (1) only contains even order derivatives of
in (2), the integral form (2) is called integral form in Galerkin method. Since A is self adjoint, the BVP (1) only contains even order derivatives of![]() . We transfer half of the differentiation from
. We transfer half of the differentiation from ![]() to v using integration by parts in the first term in (2) and collect those terms that contain both
to v using integration by parts in the first term in (2) and collect those terms that contain both ![]() and v and define them collectively as
and v and define them collectively as ![]() and those that contain only v and define them as
and those that contain only v and define them as![]() , hence we can write the following.
, hence we can write the following.
![]() (3)
(3)
Each term in ![]() contains both
contains both ![]() and v but more importantly the orders of derivatives of
and v but more importantly the orders of derivatives of ![]() and v in each term is same (i.e.
and v in each term is same (i.e. ![]() is symmetric), thus
is symmetric), thus
![]() (4)
(4)
and since A is linear, ![]() is bilinear in
is bilinear in ![]() and
and ![]() is linear in v. Hence in this case quadratic functional
is linear in v. Hence in this case quadratic functional ![]() is possible and is given by
is possible and is given by
![]() (5)
(5)
The integral form (3) is called weak form of (1). Due to the fact that (2) is integral form in Galerkin method, the weak form (3) is called integral form in Galerkin method with weak form (GM/WF). The quadratic functional ![]() has physical significance as explained in reference [35] . If (1) represents a BVP associated with
has physical significance as explained in reference [35] . If (1) represents a BVP associated with
linear elasticity in solid mechanics, then ![]() is strain energy,
is strain energy, ![]() is potential energy of loads and
is potential energy of loads and
![]() is the total potential energy of the system described by (1).
is the total potential energy of the system described by (1).
Theorem 4.1. The weak form ![]() resulting from GM/WF for self adjoint differential operator A in
resulting from GM/WF for self adjoint differential operator A in ![]() in which
in which ![]() is symmetric is variationally consistent.
is symmetric is variationally consistent.
Proof. Variational consistency of the weak form ![]() requires that there exist a functional
requires that there exist a functional ![]() such that
such that ![]() gives the weak form, the Euler’s equation resulting from
gives the weak form, the Euler’s equation resulting from ![]() is the BVP, and
is the BVP, and ![]() yields unique extremum principle. Following Section 4.1 the existence of the functional
yields unique extremum principle. Following Section 4.1 the existence of the functional ![]() is by construction (Equation (5))
is by construction (Equation (5))
![]()
If ![]() is differentiable in
is differentiable in![]() , then
, then ![]() is a necessary condition for an extremum of
is a necessary condition for an extremum of![]() . Using
. Using ![]() (due to GM/WF),
(due to GM/WF),
![]()
Since ![]() is symmetric, we obtain
is symmetric, we obtain
![]()
or
![]()
The unique extremum principle (or sufficient condition) is given by
![]()
Hence, a unique extremum principle.
To show that the Euler’s equation resulting from the weak form is in fact the BVP, we just have to transfer differentiation back to f (or fh) from v in the weak form using integration by parts. This is rather straightforward. Thus, the weak form ![]() resulting from the GM/WF is variationally consistent.
resulting from the GM/WF is variationally consistent. ![]() implies that a
implies that a ![]() from the weak form minimizes
from the weak form minimizes![]() ,
,
![]() □
□
Theorem 4.2. Let ![]() be a BVP in which A is self adjoint and let
be a BVP in which A is self adjoint and let ![]() be weak form resulting from GM/WF in which
be weak form resulting from GM/WF in which ![]() and
and![]() , then
, then ![]() has best approximation property in
has best approximation property in ![]() -norm. That is, if
-norm. That is, if![]() ,
, ![]() being theoretical solution, then
being theoretical solution, then
![]()
Proof.
a)
![]()
![]()
Choosing ![]()
![]()
Hence,
![]()
or
![]()
This implies that no element of V is a better approximation of ![]() than
than![]() , the solution for the weak form when measured in
, the solution for the weak form when measured in ![]() as e is
as e is ![]() -orthogonal to every element v of V. This is called the best approximation property of GM/WF for self adjoint operators.
-orthogonal to every element v of V. This is called the best approximation property of GM/WF for self adjoint operators.
b) For any ![]()
![]()
But![]() , hence
, hence
![]()
Since ![]() we have
we have
![]()
![]()
![]()
Thus,
![]()
or
![]()
or
![]()
That is, error in ![]() in B-norm is the lowest compared to any other solution w. This completes the proofs of a) and b). □
in B-norm is the lowest compared to any other solution w. This completes the proofs of a) and b). □
4.2. GM/WF for Non-Self Adjoint and Non-Linear Operators
Theorem 4.3. Let ![]() in
in ![]() be a BVP in which A is a non-self adjoint differential operator. Let
be a BVP in which A is a non-self adjoint differential operator. Let ![]() be all possible weak forms. Then all such integral forms are variationally inconsistent.
be all possible weak forms. Then all such integral forms are variationally inconsistent.
Proof. Let there exist a functional ![]() such that
such that ![]() yield the weak form
yield the weak form![]() . Since A is non-self adjoint,
. Since A is non-self adjoint, ![]() is bilinear but not symmetric (i.e.
is bilinear but not symmetric (i.e.![]() ), hence
), hence
![]()
is not possible because ![]() is not symmetric. Therefore,
is not symmetric. Therefore, ![]() is not a unique extremum principle. Thus, the integral form
is not a unique extremum principle. Thus, the integral form ![]() with
with ![]() is VIC when the differential operator is non-self adjoint. □
is VIC when the differential operator is non-self adjoint. □
Theorem 4.4. Let ![]() in
in ![]() be a BVP in which A is a non-linear differential operator and let
be a BVP in which A is a non-linear differential operator and let ![]() be all possible weak forms of
be all possible weak forms of ![]() in
in![]() . Then, all such integral forms or weak forms are variationally inconsistent.
. Then, all such integral forms or weak forms are variationally inconsistent.
Proof. Let there exist a functional ![]() such that
such that ![]() yields the integral form
yields the integral form![]() . Since the differential operator A is non-linear,
. Since the differential operator A is non-linear, ![]() is linear in v but not linear in
is linear in v but not linear in ![]() and
and ![]() is linear in v. Therefore, the second variation of I
is linear in v. Therefore, the second variation of I
![]()
is a function of ![]() due to the fact that
due to the fact that ![]() is a non-linear function of
is a non-linear function of![]() . Thus,
. Thus, ![]() does not represent a unique extremum principle and, hence, the integral form or weak form
does not represent a unique extremum principle and, hence, the integral form or weak form ![]() is VIC. □
is VIC. □
4.3. Least-Squares Method Based on Residual Functional: Self-Adjoint and Non-Self-Adjoint Operators
Theorem 4.5. The integral form in least-squares method based on residual functional is variationally consistent when the BVP is described by self adjoint differential operator.
Proof. Consider the BVP
![]()
in which A is self adjoint. Let ![]() be an approximation of
be an approximation of ![]() over discretization
over discretization ![]() of
of![]() . Let
. Let
![]()
be residual function. We define residual functional
![]()
If ![]() is differentiable in
is differentiable in ![]() then the necessary condition is given by
then the necessary condition is given by![]() .
.
![]()
or
![]()
or
![]()
![]() is bilinear and symmetric and
is bilinear and symmetric and ![]() is linear.
is linear.
![]()
Hence, the integral form resulting from ![]() is variationally consistent. □
is variationally consistent. □
Theorem 4.6. The integral form in least-squares method based on residual functional is variationally consistent when the BVP is described by non-self adjoint operator.
Proof. Since non-self adjoint operators are linear the proof of this theorem is same as that for self adjoint operators (Theorem 4.5) which are also linear. □
4.4. Least-Squares Method Based on Residual Functional for Non-Linear Operators
Theorem 7 Let ![]() in
in ![]() be a boundary value problem in which A is a non-linear differential oper-
be a boundary value problem in which A is a non-linear differential oper-
ator. Let ![]() be approximation of
be approximation of ![]() in
in![]() , discretization of
, discretization of ![]() and let
and let ![]() be the re-
be the re-
sidual function in![]() . Then the integral form resulting from the first variation of the residual functional
. Then the integral form resulting from the first variation of the residual functional ![]() set to zero is VC provided
set to zero is VC provided ![]() and the system of non-linear algebraic equations resulting from
and the system of non-linear algebraic equations resulting from ![]() are solved using Newton-Raphson or Newton’s linear method.
are solved using Newton-Raphson or Newton’s linear method.
Proof. Since A is non-linear, E is a non-linear function of![]() , hence
, hence ![]() is a function of
is a function of![]() .
.
![]()
If ![]() is differentiable in
is differentiable in![]() , then
, then
![]()
Hence, ![]() is a necessary condition.
is a necessary condition.
![]()
![]()
or
![]()
or
![]()
Also
![]()
is not possible. Hence, we do not have a unique extremum principle. At this stage, the least-squares process is VIC. We rectify the situation in the following.
We note that based on the necessary condition ![]() must hold. Since
must hold. Since ![]() is a non-linear function of
is a non-linear function of![]() , we must find a
, we must find a ![]() iteratively that satisfies
iteratively that satisfies![]() . Let
. Let ![]() be an initial (or assumed) solution, then
be an initial (or assumed) solution, then
![]()
Let ![]() be a change in
be a change in ![]() such that
such that
![]()
Expanding ![]() in Taylor series about
in Taylor series about ![]() and retaining only up to linear terms in
and retaining only up to linear terms in ![]() (Newton- Raphson or Newton’s linear method)
(Newton- Raphson or Newton’s linear method)
![]()
Therefore
![]()
But![]() . Hence
. Hence
![]()
Thus, in order for the coefficient matrix ![]() to be positive-definite,
to be positive-definite,
![]()
This gives a unique extremum principle. The improved value of ![]() is given by
is given by
![]()
We choose ![]() such that
such that![]() . This is referred to as line search. With this approximation of
. This is referred to as line search. With this approximation of![]() , the integral form
, the integral form ![]() is variationally consistent. £
is variationally consistent. £
Remarks
1) Justification for approximating ![]() is important to discuss.
is important to discuss.
2) We note that
![]()
Justification of ![]() is only necessary in the asymptotic range of convergence as the a priori error estimation only holds in this range, thus establishing best approximation property of LSM method in some norm is also only required in this range.
is only necessary in the asymptotic range of convergence as the a priori error estimation only holds in this range, thus establishing best approximation property of LSM method in some norm is also only required in this range.
![]()
In the asymptotic range ![]() in the pointwise sense if the approximation spaces are minimally conforming to ensure that all integrals over
in the pointwise sense if the approximation spaces are minimally conforming to ensure that all integrals over ![]() are Riemann. When
are Riemann. When ![]()
![]() then
then![]() , hence
, hence ![]() is valid. Further discussion on the validity of this approximation can be found in reference [35] .
is valid. Further discussion on the validity of this approximation can be found in reference [35] .
Theorem 4.8. The integral form resulting from the least-squares method based on residual functional has best approximation property in L2-norm of E.
Proof. From Section 4.3, we have
![]()
or
![]()
For theoretical or exact solution![]() , we have
, we have
![]()
Hence,
![]()
Thus, ![]() or
or ![]() is orthogonal to
is orthogonal to ![]() (dual of
(dual of![]() ). We note that
). We note that
![]()
That is L2-norm of E obtained using fh is lowest out of all![]() . Hence, LSP has best approximation property in L2-norm of E or
. Hence, LSP has best approximation property in L2-norm of E or![]() . £
. £
Theorem 4.9. A variationally consistent integral form has a best approximation property in some associated norm. Conversely, if an integral form has a best approximation property in some norm, then it is variationally consistent.
Proof. Proof of this theorem follows due to the fact that VC integral form in GM/WF has best approximation property in B-norm because ![]() is bilinear and symmetric. The integral form in the LSP is also VC but LSP has best approximation property in L2-norm of E. Both GM/WF and LSP are VC but have best approximation property in different norms. In both cases, VC integral form is not possible without best approximation property and the best approximation property is not possible without VC integral form. This is obviously due to the fact that they both require the functional
is bilinear and symmetric. The integral form in the LSP is also VC but LSP has best approximation property in L2-norm of E. Both GM/WF and LSP are VC but have best approximation property in different norms. In both cases, VC integral form is not possible without best approximation property and the best approximation property is not possible without VC integral form. This is obviously due to the fact that they both require the functional ![]() to be bilinear and symmetric. As long as this holds, how
to be bilinear and symmetric. As long as this holds, how ![]() is derived is not important. £
is derived is not important. £
We note that
1) Since the integral forms for non-self adjoint and non-linear differential operators are VIC in GM/WF, the approximation ![]() from GM/WF does not have best approximation property in B-norm (Theorem 4.9).
from GM/WF does not have best approximation property in B-norm (Theorem 4.9).
2) Lack of best approximation property and lack of VC of the integral form resulting from GM/WF for non- self adjoint and non-linear differential operators are both obviously due to the fact that the functional ![]() in the weak forms is not symmetric.
in the weak forms is not symmetric.
3) In LSP for all classes of differential operator ![]() is minimized, therefore
is minimized, therefore ![]() has best approximation property in E-norm
has best approximation property in E-norm
![]() .
.
4) We note that variational consistency of the integral form holds for all choices of h, p, and k whereas the best approximation property only holds in the asymptotic range.
4.5. Integral Forms Based on Other Methods of Approximation
The integral forms used in finite element method based on Petrov-Galerkin method, Galerkin method, and weighted residual method are not considered as these always yield integral forms that are variationally inconsistent. Hence, when using these integral forms computations may not even be possible.
4.6. General Remarks
1) We have established that GM/WF yields VC integral form only for self adjoint operators when the functional ![]() in the integral form is symmetric and this method has best approximation property in B-norm.
in the integral form is symmetric and this method has best approximation property in B-norm.
2) LSP based on residual functional yields VC integral forms for self adjoint, non-self adjoint, and non-linear (in the asymptotic range) differential operators and has best approximation property in E-norm.
3) VC integral form implies best approximation property in some norm and vice versa.
4) Best approximation property is necessary in a priori error estimation (in the asymptotic range), as shown in subsequent sections.
5) In general, when using GM, PGM, WRM, etc. error estimation is not possible as in these methods the approximation ![]() of
of ![]() does not have best approximation property in any norm.
does not have best approximation property in any norm.
5. A Priori Error Estimates: GM/WF and LSP
We consider simple model problems to demonstrate the best approximation properties of GM/WF for self adjoint operators and LSP for linear operators and present derivations of the a priori error estimates and convergence rates when![]() . These estimates are derived using model problems (as illustrations) and are then generalized for all BVPs.
. These estimates are derived using model problems (as illustrations) and are then generalized for all BVPs.
5.1. Model Problem 1: GM/WF
Consider the following BVP:
![]() (6)
(6)
![]() (7)
(7)
GM/WF for (6) with BCs (7) gives
![]() (8)
(8)
Let ![]() be the finite element approximation of
be the finite element approximation of![]() , then we have
, then we have
![]() (9)
(9)
Using (8) and (9) and since![]() , v in (9) is also in V and we have
, v in (9) is also in V and we have
![]() (10)
(10)
Theorem 5.1. For any ![]() we have
we have
![]()
Proof.
![]()
Since
![]()
we can choose ![]() as both
as both![]() , then
, then
![]()
Hence,
![]()
Using Cauchy-Schwarz inequality [35]
![]()
or
![]()
or
![]()
That is, in this case for the model problem (6) - (7) the derivative of ![]() has the best approximation property in L2-norm. Alternatively,
has the best approximation property in L2-norm. Alternatively, ![]() has best approximation property in B-norm. This completes the proof. £
has best approximation property in B-norm. This completes the proof. £
5.2. Model Problem 2: LSP
Consider the following BVP described by non-self adjoint differential operator.
![]() (11)
(11)
![]() (12)
(12)
LSP based on residual functional gives (for![]() )
)
![]() (13)
(13)
![]() is approximation of
is approximation of ![]() over
over![]() . This integral form is VC. Also for theoretical solution
. This integral form is VC. Also for theoretical solution
![]() (14)
(14)
Setting ![]() in (14)
in (14)
![]() (15)
(15)
Subtracting (13) from (15)
![]() (16)
(16)
Using interpolant ![]() of
of ![]() (interpolant matches
(interpolant matches ![]() at end nodes);
at end nodes);![]() , let
, let![]() , then we have
, then we have
![]() (17)
(17)
We note that![]() , hence
, hence
![]() (due to (5.11)) (18)
(due to (5.11)) (18)
Thus, (17) reduces to
![]() (19)
(19)
Using Cauchy-Schwarz inequality
![]() (20)
(20)
Thus,
![]() (21)
(21)
That is L2-norm of the derivative of error ![]() is bounded by the finite element interpolant. Using proposition 5.1 (shown subsequently) and (21), we can write
is bounded by the finite element interpolant. Using proposition 5.1 (shown subsequently) and (21), we can write
![]() (22)
(22)
L2-norm of e; that is, ![]() for LSP is derived using Aubin-Nitsche trick (Oden and Carey [33] and Reddy [34] ). We consider details in the following.
for LSP is derived using Aubin-Nitsche trick (Oden and Carey [33] and Reddy [34] ). We consider details in the following.
Consider the same BVP (for![]() ),
),
![]() (23)
(23)
Let![]() . Assume that w is the solution of the second order differential equation
. Assume that w is the solution of the second order differential equation
![]() (24)
(24)
The finite element interpolant ![]() (
(![]() ) satisfies
) satisfies
![]() (25)
(25)
![]() (using (5.19)) (26)
(using (5.19)) (26)
Consider
![]() (27)
(27)
Using integration by parts and the fact that ![]() at
at ![]() and
and ![]() at
at ![]() and
and ![]() (orthogonal property)
(orthogonal property)
![]() (28)
(28)
Hence, (using Cauchy-Schwarz inequality)
![]() (29)
(29)
Dividing by ![]()
![]() (30)
(30)
We make the following remarks.
1) For a first order BVP, the rate of convergence of the L2-norm of the error in the finite element solution is proportional to ![]() and the rate of convergence of the L2-norm of the derivative of the error is proportional to h.
and the rate of convergence of the L2-norm of the derivative of the error is proportional to h.
2) These estimates are same as those for a second order BVP when using GM/WF in which the integral form is variationally consistent.
General Remarks
1) The error estimates have been derived for a second order BVP using GM/WF in which the integral form is VC and the local approximation is linear (![]() ) over an element. In case of LSP the BVP is first order ODE, the integral form is VC, and
) over an element. In case of LSP the BVP is first order ODE, the integral form is VC, and ![]() for local approximation.
for local approximation.
2) We note that the integral forms in both cases are VC and contain only up to first order derivatives, hence the reason for same convergence rates of ![]() and
and ![]() even though in case of GM/WF the BVP is a second order ODE and in case of LSP it is only a first order ODE. This is rather significant to note that VC of the integral form and the highest order of the derivative in the integral form control the rates of convergence.
even though in case of GM/WF the BVP is a second order ODE and in case of LSP it is only a first order ODE. This is rather significant to note that VC of the integral form and the highest order of the derivative in the integral form control the rates of convergence.
3) We need to extend these estimates for higher degree local approximation (i.e. p-level of “p”).
4) The order of approximation space k needs to be incorporated in the error estimates.
5.3. Proposition and Proof
Proposition 1 Let the theoretical solution ![]() of (6) - (7) be at least of class
of (6) - (7) be at least of class ![]() and let
and let ![]() be approxi-
be approxi-
mation of ![]() over the discretization
over the discretization ![]() of
of ![]() in which
in which ![]() is an element e. Let h be the characteristic length of
is an element e. Let h be the characteristic length of ![]() such that
such that![]() . Let
. Let ![]() be interpolant of
be interpolant of ![]() that agrees
that agrees
with ![]() at the nodes [i.e.
at the nodes [i.e.![]() ,
,![]() ]. Then
]. Then
a)
![]() (31)
(31)
b)
![]() (32)
(32)
c) When (31) and (32) hold, the following hold
![]() (33)
(33)
![]() (34)
(34)
![]() (35)
(35)
in which
![]() (36)
(36)
Proof. Consider linear ![]() and
and ![]() (i.e.
(i.e.![]() ).
).
For an element e let ![]() be the interpolation error between f and inter-
be the interpolation error between f and inter-
polant![]() . Since
. Since ![]() vanishes at
vanishes at ![]() and
and ![]() of an element e, by virtue of Rolle’s theorem there ex- ists at least one point
of an element e, by virtue of Rolle’s theorem there ex- ists at least one point ![]() between
between ![]() and
and ![]() at which
at which![]() . Then for any x
. Then for any x
![]() (37)
(37)
Since ![]() is linear,
is linear, ![]() implies that
implies that
![]() (38)
(38)
Applying Cauchy-Schwarz inequality to (37) and using (38)
![]() (39)
(39)
![]() (40)
(40)
![]() (41)
(41)
![]() (42)
(42)
or
![]() (43)
(43)
Let
![]() (44)
(44)
Hence for![]() , we can write
, we can write
![]() (45)
(45)
This proves (32).
Likewise (since![]() ),
),
![]() (46)
(46)
Applying Cauchy-Schwarz inequality
![]() (47)
(47)
Substituting from (43) into (47)
![]() (48)
(48)
Hence,
![]() (49)
(49)
Using (44), (49) reduces to
![]() (50)
(50)
This proves (31):
![]() (51)
(51)
Substituting ![]() from (40) into (51)
from (40) into (51)
![]() (52)
(52)
![]() (53)
(53)
![]() (54)
(54)
![]() (55)
(55)
Thus,
![]() (56)
(56)
Hence,
![]() (57)
(57)
This proves (33).
Consider
![]() (58)
(58)
or
![]() (59)
(59)
Using Cauchy-Schwarz inequality
![]() (60)
(60)
![]() (61)
(61)
Substituting from (40)
![]() (62)
(62)
![]() (63)
(63)
![]() (64)
(64)
![]() (65)
(65)
![]() (66)
(66)
![]() (67)
(67)
Hence
![]() (68)
(68)
Now
![]() (69)
(69)
Using (56) and (68), we have
![]() (70)
(70)
![]() (71)
(71)
![]() (72)
(72)
Hence
![]() (73)
(73)
This proves (35).
Remarks
From theorem 5.1, we have
![]() (74)
(74)
and
![]() (75)
(75)
Hence using (74), (75), (33), and (34), we finally have
![]() (76)
(76)
and
![]() (77)
(77)
and likewise
![]() (78)
(78)
5.4. Proposition and Proof
Proposition 5.2. The derivation of the error estimates in proposition 1 are presented for model problem 1 using GM/WF in which the operator is self adjoint, hence the weak form is VC. In model problem 2 (Section 5.2) the differential operator is non-self adjoint and the error estimates are derived for LSP in which the integral form is also VC. In this section we consider a more general approach of deriving a priori error estimates for arbitrary degree of approximation p only based on the assumption that the integral form is VC.
If the integral form resulting from a method of approximation is VC, then the following hold.
![]() (79)
(79)
And if
![]() (80)
(80)
then
![]() (81)
(81)
In (81), ![]() is the highest order of the derivative in the differential operator A. The constants
is the highest order of the derivative in the differential operator A. The constants![]() ,
, ![]() ,
, ![]() , and
, and ![]() do not depend upon h and p.
do not depend upon h and p.
Proof. Consider one dimensional BVP:
![]() (82)
(82)
Let ![]() be discretization of
be discretization of ![]() in which
in which ![]() is an element e. Let
is an element e. Let ![]() be finite element approximation of
be finite element approximation of ![]() over
over ![]() such that
such that ![]() in which
in which ![]() is local approximation of
is local approximation of ![]() over
over![]() .
.
Let ![]() and
and ![]() be interpolants of
be interpolants of ![]() of class
of class ![]() over
over ![]() and
and ![]() such that at the nodes
such that at the nodes ![]() agrees with the theoretical solution
agrees with the theoretical solution![]() . Thus, error estimation reduces to estimating error between
. Thus, error estimation reduces to estimating error between ![]() and
and ![]() over an element
over an element ![]() of length
of length![]() . When
. When ![]() is analytic, it can be expanded in Taylor series in
is analytic, it can be expanded in Taylor series in ![]() over
over ![]() about some point j.
about some point j.
![]() (83)
(83)
Consider a ![]() over
over ![]() of degree p resulting from a VC integral form (hence, ensuring well-behaved solution), then the local approximation
of degree p resulting from a VC integral form (hence, ensuring well-behaved solution), then the local approximation ![]() at the same point j can also be written as (assuming
at the same point j can also be written as (assuming ![]() agrees with
agrees with ![]() up to degree of p),
up to degree of p),
![]() (84)
(84)
Subtracting (84) from (83), we obtain
![]() (85)
(85)
![]() (86)
(86)
![]() (87)
(87)
Let
![]() (88)
(88)
Then
![]() (89)
(89)
Therefore
![]() (90)
(90)
Using (83)-(90), it is rather straightforward to establish
![]() (91)
(91)
and by induction
![]() (92)
(92)
Using (90) and (92), we can establish that
![]() (93)
(93)
£
Remarks
1) The estimates in (92) and (93) apply to VC integral forms regardless of the method of approximation. Thus, these estimates hold for GM/WF for self adjoint operators and also hold for LSP for all three classes of differential operators.
2) The local approximations used are always of class![]() .
.
3) The constants![]() ,
, ![]() , and
, and ![]() do not depend on h and p.
do not depend on h and p.
4) The estimates (92) and (93) apply to all finite element processes in which the integral form is variationally consistent.
5) From (92) and (93), we note that progressively increasing order of derivatives of the finite element solution converge progressively slower. That is
![]() (94)
(94)
![]() (95)
(95)
and so on. Likewise
![]() (96)
(96)
![]() (97)
(97)
and so on. From (95) and (97), we note that convergence rate in H1-norm is controlled by the convergence rate of the seminorm ![]() (i.e. highest order derivative in
(i.e. highest order derivative in![]() ). This property holds universally for all operators and integral forms as long as they are variationally consistent.
). This property holds universally for all operators and integral forms as long as they are variationally consistent.
6) When examining![]() , if the highest order of derivative in E is 2m, then we have
, if the highest order of derivative in E is 2m, then we have
![]() (98)
(98)
5.5. Convergence Rates
In this section, we present details of the convergence rates of various error norms for finite element solutions obtained using GM/WF for self adjoint operators when ![]() is symmetric and LSP for all three classes of differential operators. We recall that when the integral form has best approximation property in some norm, hence is variationally consistent, we have the following a priori error estimate (derived for 1D BVP, Equation (93)) in the asymptotic range:
is symmetric and LSP for all three classes of differential operators. We recall that when the integral form has best approximation property in some norm, hence is variationally consistent, we have the following a priori error estimate (derived for 1D BVP, Equation (93)) in the asymptotic range:
![]() (99)
(99)
Taking log of both sides
![]() (100)
(100)
or
![]() (101)
(101)
in which
![]() (102)
(102)
We note that (101) is the equation of a straight line (when we use equality) in xy-space in which m is the slope and C is the y-intercept. That is, if we plot ![]() versus
versus ![]() on an xy-plot, then we obtain a straight
on an xy-plot, then we obtain a straight
line whose slope is ![]() and intercept is
and intercept is![]() . Slope
. Slope ![]() is called the rate of conver-
is called the rate of conver-
gence of![]() . Higher values of
. Higher values of ![]() imply faster convergence of
imply faster convergence of ![]() to
to ![]() measured in
measured in![]() . Equation (101) can be expressed in terms of total degrees of freedom which is perhaps more appealing in applications as dofs are more easily accessible than characteristic length or size “h” of the discretization
. Equation (101) can be expressed in terms of total degrees of freedom which is perhaps more appealing in applications as dofs are more easily accessible than characteristic length or size “h” of the discretization![]() . As the discretization
. As the discretization ![]() is refined, the characteristic length h reduces and the total dofs increase, thus dofs are inversely proportional to h,
is refined, the characteristic length h reduces and the total dofs increase, thus dofs are inversely proportional to h,
![]() (103)
(103)
Using ![]() in (100) and since
in (100) and since ![]() we obtain
we obtain
![]() (104)
(104)
We keep in mind that dofs in (104) are purely due to uniform mesh refinement. Thus, in order to determine convergence rate of ![]() for finite element processes with VC integral forms we need to plot
for finite element processes with VC integral forms we need to plot ![]() versus
versus ![]() and determine the slope of this curve
and determine the slope of this curve![]() , which is the convergence rate in the asymptotic range. For a sequence of fixed discretizations, as p increases convergence rate increases linearly.
, which is the convergence rate in the asymptotic range. For a sequence of fixed discretizations, as p increases convergence rate increases linearly.
Remarks
I) We note that ![]() requires knowledge of theoretical solution
requires knowledge of theoretical solution![]() , which may not be possible to determine for a practical application.
, which may not be possible to determine for a practical application.
II) When the approximation space ![]() is minimally conforming or of higher order (i.e.
is minimally conforming or of higher order (i.e. ![]() for integrals over
for integrals over ![]() to be Riemann or
to be Riemann or ![]() if the Lebesgue integrals over
if the Lebesgue integrals over ![]() are accepta-
are accepta-
ble), then ![]() in which the residual function can be computed using
in which the residual function can be computed using ![]() over
over
![]() and
and ![]() over
over![]() .
.
![]() (105)
(105)
using ![]() and taking log of both sides
and taking log of both sides
![]() (106)
(106)
The dofs in (106) are also due to uniform h-refinement. Since ![]() does not require theoretical solution
does not require theoretical solution![]() ,
,
it can be computed using![]() . Equation (106) can be used for any application without the knowledge of
. Equation (106) can be used for any application without the knowledge of
theoretical solution as long as the approximation space is minimally conforming or of higher order than minimally conforming.
5.6. Proposition and Proof
Proposition 5.3. When local approximation ![]() is of progressively higher order global differentiability, that is, in
is of progressively higher order global differentiability, that is, in ![]() scalar product spaces for progressively increasing k, the accuracy of the finite element solution progressively improves. In this proposition we answer two important questions:
scalar product spaces for progressively increasing k, the accuracy of the finite element solution progressively improves. In this proposition we answer two important questions:
1) Dependence of the a priori error estimates derived so far for local approximations of class ![]() on the order of the space k; that is, if the local approximations are in
on the order of the space k; that is, if the local approximations are in ![]() space how do the a priori estimates change and the influence of k on convergence rate.
space how do the a priori estimates change and the influence of k on convergence rate.
2) The influence of the order k of the approximation space on the accuracy of the finite element computation.
Of course (1) and (2) are interdependent because when we have determined (1), the assessment of accuracy may be inferred from it.
The following a priori error estimate derived for 1D BVPs using ![]() p-version local approximation can be extended when the local approximations are in
p-version local approximation can be extended when the local approximations are in ![]() spaces using the following two important considerations or properties of local approximations in
spaces using the following two important considerations or properties of local approximations in ![]() spaces:
spaces:
![]() (107)
(107)
Property I
We consider a simple illustration of a 1D discretization using three node p-version hierarchical local approximation finite elements in ![]() space. Let m be the number of elements in the discretization, then the total degrees of freedom (dofs) are given by
space. Let m be the number of elements in the discretization, then the total degrees of freedom (dofs) are given by
![]() (108)
(108)
p is the degree of local approximation (assumed same for all elements of the discretization). Let us choose a p-level, say nine (9) and a one hundred (100) element discretization, then using (108) we can determine total degrees of freedom for ![]() corresponding to the local approximations of class
corresponding to the local approximations of class![]() ,
, ![]() , ∙∙∙,
, ∙∙∙,![]() .
.
From Table 1, we observe that as k increases (i.e. progressively higher order local approximations) the total degrees of freedom are progressively reduced. This is a significant property of the higher order local approximations. From Table 1, we note that for![]() , 901 dofs are reduced to 802 in the case of
, 901 dofs are reduced to 802 in the case of ![]() without much effect on accuracy of the solution. The same holds for progressively higher order local approximations
without much effect on accuracy of the solution. The same holds for progressively higher order local approximations![]() ,
, ![]() , and so on; that is, the dofs continue to reduce with progressively increasing order of space without much effect on the accuracy. This behavior of the solution accuracy (say in
, and so on; that is, the dofs continue to reduce with progressively increasing order of space without much effect on the accuracy. This behavior of the solution accuracy (say in![]() ) holds regardless of the type of differential operator and regardless of the method of approximation used to oconstruct the integral form as long as the integral form is variationally consistent. Figure 2 shows typical plots of
) holds regardless of the type of differential operator and regardless of the method of approximation used to oconstruct the integral form as long as the integral form is variationally consistent. Figure 2 shows typical plots of ![]() versus dofs at
versus dofs at ![]() for solutions of classes
for solutions of classes![]() ,
, ![]() , and
, and![]() . Typical points A, B, C correspond to solutions of classes
. Typical points A, B, C correspond to solutions of classes![]() ,
, ![]() , and
, and ![]() for the same discretization and p-level (i.e. fixed h and p), with almost same value of
for the same discretization and p-level (i.e. fixed h and p), with almost same value of ![]() but progressively reducing degrees of freedom. In view of the a priori error estimate (107) we can conclude that if h and p are fixed, then the dependence of the a priori estimate on k lies in
but progressively reducing degrees of freedom. In view of the a priori error estimate (107) we can conclude that if h and p are fixed, then the dependence of the a priori estimate on k lies in![]() ,
, ![]() [i.e.
[i.e. ![]() in (107) and
in (107) and ![]() in (98)].
in (98)].
Property II
If we choose ![]() and if
and if ![]() is the interpolant that agrees with
is the interpolant that agrees with ![]() at the inter-element
at the inter-element
nodes of the discretization; that is, ![]() agree with
agree with ![]() corre-
corre-
sponding to local approximations of classes ![]() respectively, then in the consideration of the a priori error estimates we only need to consider (
respectively, then in the consideration of the a priori error estimates we only need to consider (![]() ) (i.e. interior of the element). This suggests that in a priori estimate in (98) (for example) only
) (i.e. interior of the element). This suggests that in a priori estimate in (98) (for example) only ![]() depends on k. That is, (98) holds when
depends on k. That is, (98) holds when ![]() except that
except that![]() .
.
![]()
Table 1. Total dofs for a 100 element discretization at p = 9 for different values of the order of space k.
![]()
Figure 2. Typical ![]() versus dofs behavior for k = 1, 2, and 3.
versus dofs behavior for k = 1, 2, and 3.
Remarks
1) From properties I and II it is clear that when![]() , in the error estimate (98) the terms
, in the error estimate (98) the terms ![]() and likewise the terms
and likewise the terms ![]() in (107) remain unaffected. Only the coefficients
in (107) remain unaffected. Only the coefficients ![]() and
and ![]() show mild dependence on k.
show mild dependence on k.
2) In view or properties I and II, we conclude that if ![]() solutions of a BVP are to be computed for a fixed number of degrees of freedom, then progressively more degrees of freedom can be added to solutions of class
solutions of a BVP are to be computed for a fixed number of degrees of freedom, then progressively more degrees of freedom can be added to solutions of class ![]() so that the total dofs in all classes of solutions are the same. We recall that with same values of h and p in the solutions of class
so that the total dofs in all classes of solutions are the same. We recall that with same values of h and p in the solutions of class ![]() (Figure 2) remains virtually the same for all classes, however the total dofs are progressively reduced.
(Figure 2) remains virtually the same for all classes, however the total dofs are progressively reduced.
The consequence of adding more dofs (through h-refinement) with progressively increasing order of space so that in each case the dofs match with C0 solutions is clearly improved accuracy of ![]() reflected by progressively reducing
reflected by progressively reducing![]() . Clearly, in doing so the convergence rate
. Clearly, in doing so the convergence rate ![]() or
or ![]() is not affected. Thus,
is not affected. Thus, ![]() versus log(dofs) graphs for solutions of classes
versus log(dofs) graphs for solutions of classes ![]() in the asymptotic range are parallel to each other but with progressively lower values of
in the asymptotic range are parallel to each other but with progressively lower values of ![]() as shown in Figure 2. That is graph for C1 is below C0 and that of C2 is below C1 and so on, but they are all parallel.
as shown in Figure 2. That is graph for C1 is below C0 and that of C2 is below C1 and so on, but they are all parallel.
5.7. General Remarks
2) We remark again that the rates only hold in the asymptotic range.
3) The integral forms must be VC so that the best approximation property of ![]() holds in some norm in order for these estimates to remain valid. The estimates derived here hold for: (a) GM/WF for self adjoint operators when the bilinear functional
holds in some norm in order for these estimates to remain valid. The estimates derived here hold for: (a) GM/WF for self adjoint operators when the bilinear functional ![]() is symmetric and (b) for LSP based on residual functional for all three classes of differential operator.
is symmetric and (b) for LSP based on residual functional for all three classes of differential operator.
4) In case of GM/WF for non-self adjoint and non-linear operators, the a priori estimates derived here do not hold. In case of such operators the functional ![]() generally consists of a symmetric part and a non-symmetric part. With sufficient mesh refinement if we can ensure that the behavior is dominated by the symmetric part, then the estimates derived here hold in the range of calculations when asymptotic range is realized. We illustrate this aspect through model problems presented in a later section.
generally consists of a symmetric part and a non-symmetric part. With sufficient mesh refinement if we can ensure that the behavior is dominated by the symmetric part, then the estimates derived here hold in the range of calculations when asymptotic range is realized. We illustrate this aspect through model problems presented in a later section.
6. Computations of a Priori Error Estimates and Convergence Rates
In this section, we present numerical studies related to the computation of a priori error estimates and convergence rates for BVPs described by self adjoint, non-self adjoint, and non-linear differential operators in which VC integral forms are constructed using GM/WF for BVP described by self adjoint differential operators and using LSP for BVPs described by all three classes of differential operators.
6.1. Model Problem 1: Self-Adjoint Operator, 1D Diffusion Equation
We consider the 1D steady-state diffusion equation.
![]() (109)
(109)
![]() (110)
(110)
If we choose![]() ,
, ![]() ,
, ![]() ,
, ![]() , then the theoretical solution
, then the theoretical solution ![]() or
or ![]() is given by
is given by
![]() (111)
(111)
a) GM/WF: The differential operator ![]() is linear and
is linear and![]() . The integral form using GM/
. The integral form using GM/
WF is given by (over![]() )
)
![]() (112)
(112)
or
![]() (113)
(113)
![]() is bilinear and symmetric and
is bilinear and symmetric and ![]() is linear. The integral form (weak form) is VC due to the fact that
is linear. The integral form (weak form) is VC due to the fact that
![]() hence a solution
hence a solution ![]() from (113) minimizes
from (113) minimizes![]() .
.
b) LSP based on residual functional
I) LSP using higher order system (without auxiliary equation)
Using (109), referred to as the higher order differential equation or system, if we let ![]() be approximation of
be approximation of ![]() over
over ![]() then
then
![]() (114)
(114)
![]() (115)
(115)
or
![]() (116)
(116)
or
![]() (117)
(117)
![]() (118)
(118)
Hence, the integral form (117) is variationally consistent.
II) LSP using first order system
Let![]() , hence (109) can be written as a system of two first order equations.
, hence (109) can be written as a system of two first order equations.
![]() (119)
(119)
LSP for (119) follows standard procedure. Let ![]() and
and ![]() be approximations of
be approximations of ![]() and
and![]() , then
, then
![]() (120)
(120)
![]() (121)
(121)
![]() (122)
(122)
Hence the integral form (121) resulting from LSP is variationally consistent.
Remarks
I) All other methods of approximation yield VIC integral forms, hence are not considered as in such cases the a priori error estimates and the convergence rates are not valid.
II) In the numerical studies, we consider GM/WF and LSP for higher order as well as first order system of differential equations describing BVPs.
6.1.1. GM/WF
In this section, we present numerical studies for the integral form (112) for![]() , discretization of
, discretization of
![]() . We consider uniform discretizations employing three node p-version hierarchical 1D elements with local approximations in scalar product space
. We consider uniform discretizations employing three node p-version hierarchical 1D elements with local approximations in scalar product space![]() . We begin with two element uniform discretization and perform uniform mesh refinement containing 4, 8, 16, ...elements. Since in this model problem the theoretical solution
. We begin with two element uniform discretization and perform uniform mesh refinement containing 4, 8, 16, ...elements. Since in this model problem the theoretical solution ![]() is known, various error norms can be computed. We note from the description of the BVP (109) that in this case
is known, various error norms can be computed. We note from the description of the BVP (109) that in this case ![]() (highest order of the derivative in the BVP) and the integral form resulting from GM/WF contains only up to first order derivatives of the dependent variable and the test function. We consider computations using solutions of class
(highest order of the derivative in the BVP) and the integral form resulting from GM/WF contains only up to first order derivatives of the dependent variable and the test function. We consider computations using solutions of class![]() ,
, ![]() , and
, and ![]() at different p-levels with uniform mesh refinements. Computed results for solution of class
at different p-levels with uniform mesh refinements. Computed results for solution of class ![]() are shown in Figure 3. The integral form is VC and
are shown in Figure 3. The integral form is VC and![]() , the computed solution, has best approximation property in
, the computed solution, has best approximation property in ![]() -norm.
-norm.
In this case, the following a priori error estimates hold (Proposition 5.2):
![]() (123)
(123)
For this BVP, ![]() and q depends on the type of norm. Figure 3 also shows the theoretical values of the convergence rates of various error norms for solutions of class
and q depends on the type of norm. Figure 3 also shows the theoretical values of the convergence rates of various error norms for solutions of class ![]() at p-levels of 2 and 5. Graphs of the log of error norms versus log of dofs for these solutions are shown in Figure 3. We note that due to smoothness of the theoretical solution even the two element discretization yields the error norms in the asymptotic range; that is,
at p-levels of 2 and 5. Graphs of the log of error norms versus log of dofs for these solutions are shown in Figure 3. We note that due to smoothness of the theoretical solution even the two element discretization yields the error norms in the asymptotic range; that is,
![]()
Figure 3. ![]() versus log(dofs) for solutions of class C0 (GM/WF, model problem 1,
versus log(dofs) for solutions of class C0 (GM/WF, model problem 1, ![]() and 5).
and 5).
pre-asymptotic and onset of asymptotic ranges in these solutions do not appear in Figure 3. All computations are in the asymptotic range, hence onset of post-asymptotic and post-asymptotic ranges are also absent. Calculated convergence rates are in perfect agreement with the theoretical convergence rates calculated using (123). We note that in ![]() and
and ![]() error norms the integrals over
error norms the integrals over ![]() are Lebesgue, but the norms are well- behaved due to smoothness of
are Lebesgue, but the norms are well- behaved due to smoothness of![]() .
.
Figure 4 shows plots of log of various norms and seminorms versus log of degrees of freedom at ![]() and 5 for
and 5 for ![]() solutions. The computed convergence rates of various error norms and comparison with the theoretical convergence rates obtained using (123) are shown in Figure 4. The agreement is perfect. Here we note that in computing
solutions. The computed convergence rates of various error norms and comparison with the theoretical convergence rates obtained using (123) are shown in Figure 4. The agreement is perfect. Here we note that in computing ![]() and
and![]() , the integrals over
, the integrals over ![]() are Lebesgue but error norms are well-behaved due to smoothness of
are Lebesgue but error norms are well-behaved due to smoothness of![]() . Also, nearly all computations shown in Figure 4 are in the asymptotic range, except for the last point for
. Also, nearly all computations shown in Figure 4 are in the asymptotic range, except for the last point for ![]() at
at ![]() and
and ![]() at
at![]() .
.
Log of various error norms and seminorms versus log of degrees of freedom for solutions of class ![]() at
at ![]() and 7 are shown in Figure 5. Since
and 7 are shown in Figure 5. Since ![]() for
for![]() , all integrals in all error norms are Riemann over the discretization
, all integrals in all error norms are Riemann over the discretization![]() . Computed error norms using (123) and comparison with the computed convergence rates of error norm are also shown in Figure 5. We observe perfect match between the theoretical values and the computed values. Except for the last point shown in Figure 5 for
. Computed error norms using (123) and comparison with the computed convergence rates of error norm are also shown in Figure 5. We observe perfect match between the theoretical values and the computed values. Except for the last point shown in Figure 5 for ![]() at
at![]() , all other computed results are in the asymptotic range due to smoothness of
, all other computed results are in the asymptotic range due to smoothness of![]() .
.
Figure 6 shows plots of ![]() (or
(or![]() ) versus log of dof for solutions of class
) versus log of dof for solutions of class![]() ,
, ![]() , and
, and ![]()
(![]() ) at
) at![]() . All three graphs of
. All three graphs of ![]() versus log of dofs for
versus log of dofs for ![]() are parallel, confirming that the convergence rate of
are parallel, confirming that the convergence rate of ![]() is independent of the order k of the approximation space. We note that graph for
is independent of the order k of the approximation space. We note that graph for ![]() appears below
appears below ![]() and the graph for
and the graph for ![]() is below
is below ![]() confirming that for given dofs, as the order k of space is increased, the error in the computed solution
confirming that for given dofs, as the order k of space is increased, the error in the computed solution ![]() (measured in
(measured in ![]() -norm) decreases without affecting the convergence rate.
-norm) decreases without affecting the convergence rate.
The BVP in this model problem is described by a second-order differential operator (![]() ); hence,
); hence, ![]() corresponds to minimally conforming space
corresponds to minimally conforming space ![]() for which the integrals are always Riemann. However, due to smoothness of
for which the integrals are always Riemann. However, due to smoothness of![]() , when
, when ![]() (solutions of class
(solutions of class![]() ) in which case the integrals over
) in which case the integrals over ![]() are Lebesgue, the solution
are Lebesgue, the solution ![]() is expected to converge weakly to class
is expected to converge weakly to class![]() . Next we consider solutions of class
. Next we consider solutions of class
![]()
Figure 6. ![]() versus log(dofs) for solutions of classes C0, C1, and C2 at
versus log(dofs) for solutions of classes C0, C1, and C2 at ![]() (GM/WF, model problem 1).
(GM/WF, model problem 1).
![]() with
with ![]() (minimum). Numerical solutions are computed for uniform mesh refinements beginning with a two-element uniform discretization. For each discretization we calculate
(minimum). Numerical solutions are computed for uniform mesh refinements beginning with a two-element uniform discretization. For each discretization we calculate ![]() and
and![]() . Since the rate of convergence of
. Since the rate of convergence of ![]() is controlled by
is controlled by![]() , we expect the convergence rates of
, we expect the convergence rates of ![]() and
and ![]() to be nearly same. We clearly see this in Figure 7. Graphs for
to be nearly same. We clearly see this in Figure 7. Graphs for ![]() and
and ![]() are parallel, confirming the same convergence rates of
are parallel, confirming the same convergence rates of ![]() (or
(or![]() ) for solutions of class
) for solutions of class ![]() (
(![]() ) and class
) and class ![]() (
(![]() ). The convergence rate in the case of
). The convergence rate in the case of ![]() is
is![]() , whereas in the case of
, whereas in the case of ![]() is
is![]() . Plots in Figure 7 confirm that rate of convergence of error norms is independent of the order of the approximation space.
. Plots in Figure 7 confirm that rate of convergence of error norms is independent of the order of the approximation space.
6.1.2. LSP, Higher-Order System (No Auxiliary Equation)
In this study, we consider finite element formulation of model problem (109) using least-squares process based on residual functional. We consider solutions of class ![]() as well as
as well as![]() . In case of
. In case of ![]() solutions integrals over
solutions integrals over ![]() are Lebesgue whereas for solutions of class
are Lebesgue whereas for solutions of class ![]() the integrals are Riemann. Figure 8 shows plots of
the integrals are Riemann. Figure 8 shows plots of ![]() and
and ![]() versus log of dofs for p-levels of 3 and 5 calculated using uniform mesh refinement. Calculated convergence rates of various error norms are also shown in Figure 8. The theoretical convergence rates of various error norms and a comparison with calculated convergence rates is also shown in Figure 8.
versus log of dofs for p-levels of 3 and 5 calculated using uniform mesh refinement. Calculated convergence rates of various error norms are also shown in Figure 8. The theoretical convergence rates of various error norms and a comparison with calculated convergence rates is also shown in Figure 8.
Agreement between theoretical and calculated values is excellent. Here also we observe absence of pre- asymptotic and onset of asymptotic ranges due to smoothness of the theoretical solution. Some graphs for significant refinement show appearance of post-asymptotic (or onset of post-asymptotic) range.
Similar studies for solutions of class ![]() are shown in Figure 9 for
are shown in Figure 9 for![]() ;
;![]() ,
,![]() ; and
; and![]() ,
, ![]() norms at p-levels of 5 and 7. The computed convergence rates of the error norms are in perfect agreement with theoretical rates calculated using (
norms at p-levels of 5 and 7. The computed convergence rates of the error norms are in perfect agreement with theoretical rates calculated using (![]() ), shown in Figure 9.
), shown in Figure 9.
Graphs of ![]() and
and ![]() (or
(or![]() ) versus log of dofs for solutions of class
) versus log of dofs for solutions of class ![]() and
and ![]() obtained using uniform mesh refinement are shown in Figure 10. Calculated convergence rates are also shown in Figure 10. For
obtained using uniform mesh refinement are shown in Figure 10. Calculated convergence rates are also shown in Figure 10. For ![]() error norm the theoretical rate is (
error norm the theoretical rate is (![]() ) whereas for
) whereas for ![]() it is (
it is (![]() ). The theoretical convergence rates are in perfect agreement with those calculated using graphs in Figure 10. We note that
). The theoretical convergence rates are in perfect agreement with those calculated using graphs in Figure 10. We note that
![]()
Figure 8. ![]() versus log(dofs) for solutions of class C1 (LSP, model problem 1,
versus log(dofs) for solutions of class C1 (LSP, model problem 1, ![]() and 5).
and 5).
![]()
Figure 9. ![]() versus log(dofs) for solutions of class C (LSP, model problem 1, p = 5 and 7).
versus log(dofs) for solutions of class C (LSP, model problem 1, p = 5 and 7).
![]()
Figure 10. ![]() or
or ![]() versus log(dofs) for solutions of classes C1 and C2 at p = 5 (LSP, model problem 1).
versus log(dofs) for solutions of classes C1 and C2 at p = 5 (LSP, model problem 1).
![]() and
and ![]() graphs for same p-level (5) are parallel to each other and
graphs for same p-level (5) are parallel to each other and ![]() graph is below
graph is below![]() , confirming that the convergence rates for
, confirming that the convergence rates for ![]() and
and ![]() are same (i.e. independent of k), the order of space, but for
are same (i.e. independent of k), the order of space, but for ![]() the solution has better accuracy compared to
the solution has better accuracy compared to![]() .
.
Remarks. Numerical studies for LSP using auxiliary equation (i.e. a first-order system) are not presented for this model problem but will be presented for the next model problem, 1D convection-diffusion equation.
6.2. Model Problem 2: Non-Self-Adjoint Operator, 1D Convection-Diffusion Equation
We consider 1D convection-diffusion equation described by non-self adjoint operator for computing a priori error estimates and convergence rates and compare them with their theoretical values,
![]() (124)
(124)
![]() (125)
(125)
We consider![]() . Theoretical solution of (124)-(125), finite element solution using GM/WF and LSP using higher order system (no auxiliary variables) and using first order system (using auxiliary variables) is
. Theoretical solution of (124)-(125), finite element solution using GM/WF and LSP using higher order system (no auxiliary variables) and using first order system (using auxiliary variables) is
given in [35] . For this BVP, the operator ![]() is linear but
is linear but![]() , hence the in-
, hence the in-
tegral form from GM/WF is VIC, but LSP for higher order as well as first order system of differential equations is VC.
a) GM/WF: The integral form of (124)-(125) is given by (for![]() )
)
![]() (126)
(126)
![]() (127)
(127)
![]() is bilinear but not symmetric and
is bilinear but not symmetric and
![]() (128)
(128)
does not yield a unique extremum principle. Hence, the integral form (127) is VIC.
b) LSP based on residual functional:
I) Higher order system (without auxiliary equation)
In this case we use (124) without introducing auxiliary equation, that is without reducing (124) into a first order system of equations. Let ![]() be approximation of
be approximation of ![]() over
over![]() , then
, then
![]() (129)
(129)
![]() (130)
(130)
or
![]() (131)
(131)
or
![]() (132)
(132)
![]() (133)
(133)
Hence, the integral form (132) is VC.
II) First order system
Let![]() , hence (124) can be written as
, hence (124) can be written as
![]() (134)
(134)
LSP for (134) follows standard procedure (parallel to Equations (119)-(122)). Details are straightforward. See [35] for many model problems of similar type.
Remarks
1) Since GM/WF yields VIC integral form and does not have best approximation property as the operator A is not self adjoint, hence the a priori error estimates derived in earlier sections using best approximation property in B-norm do not hold in this case. Nonetheless we present numerical studies for GM/WF for this model problem to illustrate some important aspects of error norms in a later section.
2) Integral form derived using LSP is VC and has best approximation property in E-norm or![]() , I being residual functional, hence the same a priori error estimates derived for LSP for self adjoint operators hold here as well.
, I being residual functional, hence the same a priori error estimates derived for LSP for self adjoint operators hold here as well.
6.2.1. LSP: First Order System
Domain ![]() is discretized using 3-node p-version 1D elements of higher order global differentiability into 2, 4, 6, ...element uniform meshes. The solutions are computed using finite element formulation based on LSP for first order system of equations. Solutions of classes
is discretized using 3-node p-version 1D elements of higher order global differentiability into 2, 4, 6, ...element uniform meshes. The solutions are computed using finite element formulation based on LSP for first order system of equations. Solutions of classes![]() ,
, ![]() , and
, and ![]() are considered at different p-levels. For this problem the a priori estimates (123) hold as well with
are considered at different p-levels. For this problem the a priori estimates (123) hold as well with ![]() due to the fact that it is a first order system of equations. LSP has best approximation property in E-norm and the integral form is VC,
due to the fact that it is a first order system of equations. LSP has best approximation property in E-norm and the integral form is VC,
![]() (135)
(135)
First, we consider solutions of class ![]() at
at ![]() and 5 and with
and 5 and with![]() . Due to
. Due to ![]() local approximation and the first order system, integrals over
local approximation and the first order system, integrals over ![]() are Lebesgue but due to smoothness of
are Lebesgue but due to smoothness of ![]() weak convergence of computed
weak convergence of computed ![]() to
to ![]() class is expected. Figure 11 shows plots of log of various error norms versus log of the dofs at
class is expected. Figure 11 shows plots of log of various error norms versus log of the dofs at ![]() and 5. Details of the studies are also given in Figure 11. Theoretical convergence rates are in perfect agreement with the calculated rates shown in Figure 11. As p-level is increased from 2 to 5 convergence rates also show increase by 3 at
and 5. Details of the studies are also given in Figure 11. Theoretical convergence rates are in perfect agreement with the calculated rates shown in Figure 11. As p-level is increased from 2 to 5 convergence rates also show increase by 3 at ![]() compared to those at
compared to those at![]() . We clearly observe pre- asymptotic, onset of asymptotic, and asymptotic ranges in all cases. For
. We clearly observe pre- asymptotic, onset of asymptotic, and asymptotic ranges in all cases. For ![]() also observe onset of post- asymptotic and post-asymptotic ranges. We note that even though LSP does not have best approximation property in B-norm but due to the fact that the integral form is VC, the convergence rate of LSP (135) is same as those of GM/ WF for self adjoint operators (123).
also observe onset of post- asymptotic and post-asymptotic ranges. We note that even though LSP does not have best approximation property in B-norm but due to the fact that the integral form is VC, the convergence rate of LSP (135) is same as those of GM/ WF for self adjoint operators (123).
As p-level is increased convergence rate increases proportionately. Derivatives converge more slowly than functions, hence convergence rate of ![]() is one order lower than that of
is one order lower than that of ![]() or
or![]() . Since the convergence rate of
. Since the convergence rate of ![]() is dominated by the first derivative,
is dominated by the first derivative, ![]() and
and ![]() have same convergence rates (also clear from (135)).
have same convergence rates (also clear from (135)).
Solutions of class ![]() at
at ![]() and 5 are considered here. Results obtained using uniform mesh refinement are given in Figure 12. Plots of log of various error norms versus log of dofs and calculated convergence rates are shown in Figure 12 and are compared with theoretical convergence rates. Calculated and theoretical convergence rates are in perfect agreement. We note that when
and 5 are considered here. Results obtained using uniform mesh refinement are given in Figure 12. Plots of log of various error norms versus log of dofs and calculated convergence rates are shown in Figure 12 and are compared with theoretical convergence rates. Calculated and theoretical convergence rates are in perfect agreement. We note that when ![]() the convergence rates of error norms are independent of k (i.e. at
the convergence rates of error norms are independent of k (i.e. at![]() ), solutions of class
), solutions of class ![]() and
and ![]() have same convergence rates for the same norm, confirming that convergence rates of the error norms are not a function of k, the order of the approximation space. Pre-asymptotic, onset of asymptotic, and asymptotic ranges are clearly observed in Figure 12.
have same convergence rates for the same norm, confirming that convergence rates of the error norms are not a function of k, the order of the approximation space. Pre-asymptotic, onset of asymptotic, and asymptotic ranges are clearly observed in Figure 12.
Solutions of class ![]() at
at ![]() and 7 are considered next. Results obtained using uniform mesh refinement are shown in Figure 13 and are compared with the theoretical convergence rates obtained using (135). Once
and 7 are considered next. Results obtained using uniform mesh refinement are shown in Figure 13 and are compared with the theoretical convergence rates obtained using (135). Once
again the agreement is perfect. Again, we note from Figure 12 and Figure 13 that at ![]() the convergence rates are independent of k. In this case, the integrals in the computations of the error norms are always Riemann.
the convergence rates are independent of k. In this case, the integrals in the computations of the error norms are always Riemann.
Figure 14 shows plots of ![]() and
and ![]() versus log of dof for solutions of class
versus log of dof for solutions of class ![]() and
and ![]() at
at![]() . Since the differential operator has the highest derivative of order 2, the convergence rate of
. Since the differential operator has the highest derivative of order 2, the convergence rate of ![]() is expected to be same as that of
is expected to be same as that of ![]() or
or ![]() for both classes of solutions. This is confirmed in Figure 14. Convergence rate in case of
for both classes of solutions. This is confirmed in Figure 14. Convergence rate in case of ![]() and
and ![]() solutions are same (4 in this case), but
solutions are same (4 in this case), but ![]() solutions have better accuracy for a given dofs, confirming again that convergence rates of error norms or residual functional are not a function of the order k of the approximation space. Calculated rates are in perfect agreement with the theoretical rates. Figure 15 shows plots of log of
solutions have better accuracy for a given dofs, confirming again that convergence rates of error norms or residual functional are not a function of the order k of the approximation space. Calculated rates are in perfect agreement with the theoretical rates. Figure 15 shows plots of log of ![]() versus log of dofs for solution of classes
versus log of dofs for solution of classes![]() ,
, ![]() , and
, and ![]() at
at![]() . We observe same convergence rates for
. We observe same convergence rates for![]() , 2, and 3 but better accuracy of the solution with progressively increasing k. These rates for LSP match perfectly with GM/WF for self adjoint operators due to the fact that in both cases the integral forms are variationally consistent. This proves again that the best approximation property in B-norm is not a requirement for establishing convergence rate. It is the variational consistency of the integral form that matters. Clearly the LSP does not have best approximation property in B-norm, yet has same convergence rates as GM/WF for self adjoint operators due to the fact that in both cases the integral forms are variationally consistent.
, 2, and 3 but better accuracy of the solution with progressively increasing k. These rates for LSP match perfectly with GM/WF for self adjoint operators due to the fact that in both cases the integral forms are variationally consistent. This proves again that the best approximation property in B-norm is not a requirement for establishing convergence rate. It is the variational consistency of the integral form that matters. Clearly the LSP does not have best approximation property in B-norm, yet has same convergence rates as GM/WF for self adjoint operators due to the fact that in both cases the integral forms are variationally consistent.
6.2.2. GM/WF
Since the differential operator is non-self adjoint the GM/WF will yield VIC integral form in which ![]() is nonsymmetric and we lose the best approximation property in B-norm. Nonetheless we conduct some numerical experiments to monitor convergence rates of various error norms. First, we note that GM/WF in this model problem will yield the following element equations for an element e (when
is nonsymmetric and we lose the best approximation property in B-norm. Nonetheless we conduct some numerical experiments to monitor convergence rates of various error norms. First, we note that GM/WF in this model problem will yield the following element equations for an element e (when ![]() and
and![]() ). See reference [35] .
). See reference [35] .
![]() (136)
(136)
and the assembled equations for discretization ![]() are
are
![]() (137)
(137)
in which ![]() and
and![]() ,
, ![]() are due to assembly of
are due to assembly of ![]() and
and ![]() for
for![]() . As shown in reference [35] ,
. As shown in reference [35] , ![]() is due to convection term (i.e.
is due to convection term (i.e.![]() ) and
) and ![]() is due to diffusion (i.e.
is due to diffusion (i.e.![]() );
); ![]() is
is
nonsymmetric with zeros on the diagonals after ![]() and
and ![]() BCs are imposed, thus if
BCs are imposed, thus if ![]() is large, the contribution of
is large, the contribution of ![]() to
to ![]() is almost insignificant compared to the contribution of
is almost insignificant compared to the contribution of ![]() and the computations using (137) will fail. On the other hand if the discretization
and the computations using (137) will fail. On the other hand if the discretization ![]() is sufficiently refined, the con-
is sufficiently refined, the con-
tribution of ![]() to
to ![]() overshadows that of
overshadows that of ![]() and the behavior will be dominated by
and the behavior will be dominated by ![]() (i.e.
(i.e. ![]()
term in the differential operator). When this happens the integral form from GM/WF will behave like a VC inte-
gral form as it is primarily due to ![]() term in the differential operator which is self adjoint, hence the
term in the differential operator which is self adjoint, hence the
convergence rates of various error norms will be similar to GM/WF for self adjoint operator.
For numerical experiments, we consider ![]() and
and![]() . For
. For ![]() the solution gradients are more isolated near
the solution gradients are more isolated near ![]() and are higher in magnitude compared to
and are higher in magnitude compared to![]() . We consider solutions of class
. We consider solutions of class ![]() at
at ![]() for both Peclet numbers. Progressively refined uniform discretizations are used for computing solutions and error norms. Figure 16 shows error norms versus dof plots for solutions of class
for both Peclet numbers. Progressively refined uniform discretizations are used for computing solutions and error norms. Figure 16 shows error norms versus dof plots for solutions of class![]() ,
, ![]() for
for![]() . We note that due to smoothness of the solutions, the asymptotic range in which
. We note that due to smoothness of the solutions, the asymptotic range in which ![]() dominates is quickly achieved, and the computations succeed for meshes of 16 elements or more. In this range calculated convergence rates match perfectly with the theoretical rates for self adjoint operator. In this range the BVP re-
dominates is quickly achieved, and the computations succeed for meshes of 16 elements or more. In this range calculated convergence rates match perfectly with the theoretical rates for self adjoint operator. In this range the BVP re-
duces to ![]() as the contribution of
as the contribution of ![]() term in this range is insignificant. For meshes with 16 ele-
term in this range is insignificant. For meshes with 16 ele-
ments or fewer the calculated solution from (137) does not satisfy (137) when substituted in them, implying lack of equilibrium due to spuriousness of the computed solution. Figure 17 shows similar graphs for![]() . The computations fail for discretizations resulting in
. The computations fail for discretizations resulting in ![]() (meshes coarser than 256 elements) where equilibrium is not achieved, that is, calculated solution from (137) does not satisfy (137) when substituted into the equations. This is due to VIC nature of the integral form resulting from GM/WF. Correspondingly, the values of the error norms for the failed discretizations grow out of control. When
(meshes coarser than 256 elements) where equilibrium is not achieved, that is, calculated solution from (137) does not satisfy (137) when substituted into the equations. This is due to VIC nature of the integral form resulting from GM/WF. Correspondingly, the values of the error norms for the failed discretizations grow out of control. When ![]() (discretization contains 256 elements or more),
(discretization contains 256 elements or more), ![]() contribution becomes insignificant and the BVP behaves like
contribution becomes insignificant and the BVP behaves like
![]() , hence the asymptotic range is observed with calculated convergence rates of the indicated error
, hence the asymptotic range is observed with calculated convergence rates of the indicated error
norms of 3.7, 2.9, 2 are achieved compared to their theoretical values of 4, 3, 2 for self adjoint operators, rather amazingly good performance for VIC integral form.
When performing the error computations for ![]() higher than 1000 with uniform mesh refinement of 2, 4, ...elements failure of computations occurs when
higher than 1000 with uniform mesh refinement of 2, 4, ...elements failure of computations occurs when ![]() dominates the total
dominates the total ![]() as expected.
as expected.
6.2.3. LSP: Higher Order System (Without Auxiliary Equation)
In this study, we consider 1D convection-diffusion equation (124) without converting it to a system of first order equations through the use of auxiliary equation. In this case![]() ,
, ![]() is minimally conforming approximation space if the integrals over
is minimally conforming approximation space if the integrals over ![]() are to be Riemann. For
are to be Riemann. For ![]() the integrals over
the integrals over ![]() are Lebesgue and
are Lebesgue and ![]() (solutions of class
(solutions of class![]() ) is not admissible.
) is not admissible.
Error norms are computed for progressively refined uniform discretizations for ![]() (solutions of classes
(solutions of classes ![]() and
and![]() ) at p-levels of 3 and 5 for
) at p-levels of 3 and 5 for ![]() and
and ![]() and 7 for
and 7 for![]() . Plots of error norms versus dof for
. Plots of error norms versus dof for
solutions of classes ![]() and
and ![]() and the calculated convergence rates and comparisons with the theoretical values are shown in Figure 18 and Figure 19. We note that the highest order of the derivative in the mathematical model (
and the calculated convergence rates and comparisons with the theoretical values are shown in Figure 18 and Figure 19. We note that the highest order of the derivative in the mathematical model (![]() ) in this case is 2 as the convection-diffusion equation is not reduced to a first order system using auxiliary equations. Theoretical convergence rates are overall in good agreement with the calculated convergence rates confirming importance of the variational consistency of the integral form. In solutions of both classes, the convergence rate of
) in this case is 2 as the convection-diffusion equation is not reduced to a first order system using auxiliary equations. Theoretical convergence rates are overall in good agreement with the calculated convergence rates confirming importance of the variational consistency of the integral form. In solutions of both classes, the convergence rate of ![]() is higher than predicted for
is higher than predicted for![]() . In this case
. In this case ![]() whereas in case of first order system derived using auxiliary equation
whereas in case of first order system derived using auxiliary equation![]() , thus the first order system has higher convergence rate of
, thus the first order system has higher convergence rate of ![]() in the LSP.
in the LSP.
Figure 20 shows plots of ![]() versus dofs and
versus dofs and ![]() versus dofs for solutions of classes
versus dofs for solutions of classes ![]() and
and ![]() at
at![]() . Since the highest order derivative is two in the differential operator, the convergence rate of
. Since the highest order derivative is two in the differential operator, the convergence rate of ![]() is same as that of
is same as that of![]() .
. ![]() and
and ![]() solutions have same convergence rates but
solutions have same convergence rates but ![]() solutions have better accuracy for a given dofs, confirming that the convergence rates of error norm and residual functional are not a function of the order k of the approximation space. Thus, for higher order system we also observe that the rates for LSP match with GM/WF for self adjoint operators due to the fact that in both the integral forms are VC even though the two methods of approximation have best approximation property in different norms.
solutions have better accuracy for a given dofs, confirming that the convergence rates of error norm and residual functional are not a function of the order k of the approximation space. Thus, for higher order system we also observe that the rates for LSP match with GM/WF for self adjoint operators due to the fact that in both the integral forms are VC even though the two methods of approximation have best approximation property in different norms.
6.3. Model Problem 3: Non-Linear Operator, 1D Burgers Equation
We consider 1D Burgers equation described by a non-linear operator (see reference [35] ) to compute a priori error estimates and convergence rates of various error norms and compare them with their theoretical values,
![]() (138)
(138)
![]() (139)
(139)
For the studies presented in the following sections, a value of ![]() is used. Theoretical solution
is used. Theoretical solution ![]() of
of
(138) and (139) and finite element solution ![]() using GM/WF and LSP (higher order and first order systems) are given in reference [35] . Some details are given in the following as a review. It is shown [35] that in this case
using GM/WF and LSP (higher order and first order systems) are given in reference [35] . Some details are given in the following as a review. It is shown [35] that in this case
![]() which is a function of
which is a function of![]() , hence non-linear. The GM/WF yields VIC integral form. The in-
, hence non-linear. The GM/WF yields VIC integral form. The in-
tegral form from the LSP is VC with minor adjustments (see theorem 7) of little consequence but immense benefit as they yield variational consistency of the integral form.
a) GM/WF: The integral form of (138) and (139) over ![]() is given by
is given by
![]() (140)
(140)
or
![]() (141)
(141)
Functional ![]() is linear in v but not linear in
is linear in v but not linear in ![]() and is obviously not symmetric.
and is obviously not symmetric.
![]() (142)
(142)
is obviously not![]() ,
, ![]() , or
, or ![]()
![]() , hence the integral form (141) is VIC.
, hence the integral form (141) is VIC.
b) LSP based on residual functional: These can be constructed in two alternate ways, as a higher order system (138) or by recasting (138) as a system of first order equations. [(I)]
I) Higher order system
![]() (143)
(143)
and residual functional ![]() is given by
is given by
![]() (144)
(144)
![]() (145)
(145)
![]() (146)
(146)
The necessary condition ![]() is satisfied by calculating a solution using Newton’s linear method. See reference [35] for full details. The integral form in this case is variationally consistent.
is satisfied by calculating a solution using Newton’s linear method. See reference [35] for full details. The integral form in this case is variationally consistent.
II) First order system
Let![]() , then (138) reduces to
, then (138) reduces to
![]() (147)
(147)
LSP for (147) is described in detail in reference [35] and is omitted here. This integral form is also VC.
6.3.1. LSP: Higher-Order System (Without Auxiliary Equation)
For this model problem we only present studies related to convergence rates of various error norms using (138) (i.e. without recasting it as a system of first order equations). As in other problems ![]() is discretized using uniform meshes of 2, 4, 8, ...3-node p-version higher order global differentiability elements and the solutions are computed using finite element formulations based on GM/WF and LSP. In case of LSP, since the integral form is VC the same convergence rate estimates hold as in (135):
is discretized using uniform meshes of 2, 4, 8, ...3-node p-version higher order global differentiability elements and the solutions are computed using finite element formulations based on GM/WF and LSP. In case of LSP, since the integral form is VC the same convergence rate estimates hold as in (135):
![]() (148)
(148)
In this BVP,![]() . Since the differential operator has derivative of
. Since the differential operator has derivative of ![]() up to second order, the minimally conforming space in this case is
up to second order, the minimally conforming space in this case is ![]() for the integrals over
for the integrals over ![]() to be Riemann and the integrals are in Lebesgue sense when
to be Riemann and the integrals are in Lebesgue sense when![]() .
. ![]() is not admissible. Figure 21 and Figure 22 show plots of various error norms versus dofs for solutions of class
is not admissible. Figure 21 and Figure 22 show plots of various error norms versus dofs for solutions of class ![]() and
and ![]() as well as calculated and theoretical convergence rates.
as well as calculated and theoretical convergence rates.
First, we note from Figure 21 and Figure 22 large pre-asymptotic and onset of asymptotic ranges. The asymptotic range is rather limited, due to which accurate computation of convergence rates is difficult. Nonetheless we observe that for most error norms the theoretical and calculated convergence rates are in good agreement. Once again, we observe that due to VC integral form in LSP for nonlinear operators the convergence rate estimates for GM/WF for self adjoint operators and the same for LSP for linear operators hold here, again confirming the significance and importance of VC integral forms.
Figure 23 shows plots of ![]() versus dof and
versus dof and ![]() versus dof for solutions of class
versus dof for solutions of class ![]() and
and ![]() at
at![]() . Since the differential operator is second order operator, the convergence rate of
. Since the differential operator is second order operator, the convergence rate of ![]() is same as that of
is same as that of ![]() for both
for both ![]() and
and ![]() local approximations. However,
local approximations. However, ![]() solutions have better accuracy for a given dofs. We clearly observe that the convergence rate is not a function of k, the order of approximation space. Calculated convergence rates of
solutions have better accuracy for a given dofs. We clearly observe that the convergence rate is not a function of k, the order of approximation space. Calculated convergence rates of ![]() and
and ![]() are the same and are in exact agreement with the theoretical convergence rates.
are the same and are in exact agreement with the theoretical convergence rates.
6.3.2. GM/WF
Since the differential operator is non-linear the integral form from GM/WF is VIC. ![]() is not bilinear and is
is not bilinear and is
not symmetric, hence we lose best approximation property of the GM/WF in -norm. GM/WF will yield the following form of the assembled equations for ![]() (when
(when ![]() and B
and B![]() ) assuming uniform discretization (
) assuming uniform discretization (![]() ):
):
![]() (149)
(149)
in which ![]() and
and![]() .
. ![]() is symmetric.
is symmetric. ![]() is due to
is due to ![]() and
and ![]() is due to
is due to ![]() term in the differential equation. Furthermore
term in the differential equation. Furthermore ![]() has zeros on the diagonal after
has zeros on the diagonal after ![]()
and ![]() boundary conditions are imposed, thus if
boundary conditions are imposed, thus if ![]() is large, the contribution of
is large, the contribution of ![]() to
to ![]() is almost insignificant and the computations using (149) will fail. On the other hand if the discretization
is almost insignificant and the computations using (149) will fail. On the other hand if the discretization ![]() is sufficiently refined then contribution of
is sufficiently refined then contribution of ![]() to
to ![]() overshadows that of
overshadows that of ![]() and the solution behavior
and the solution behavior
will be dominated by ![]() (i.e.
(i.e. ![]() term in the differential equation). When this happens the integral form
term in the differential equation). When this happens the integral form
from GM/WF will behave like a VC integral form and the convergence rates of various error norms will be same as those of GM/WF for self adjoint operator.
For numerical studies, we consider![]() . Uniform mesh refinement is carried out for solutions of class
. Uniform mesh refinement is carried out for solutions of class ![]() at
at![]() . Figure 24 shows plots of error norms versus dofs. We note that for discretizations coarser than 128 elements the error norms correspond to erroneous computed solutions in which equilibrium condition is violated for the assembled equations. For finer discretizations (128 elements or more) asymptotic range is observed. In this range discretization is sufficiently refined so that the integral form is dominated by the diffusion term. Calculated convergence rates (of
. Figure 24 shows plots of error norms versus dofs. We note that for discretizations coarser than 128 elements the error norms correspond to erroneous computed solutions in which equilibrium condition is violated for the assembled equations. For finer discretizations (128 elements or more) asymptotic range is observed. In this range discretization is sufficiently refined so that the integral form is dominated by the diffusion term. Calculated convergence rates (of![]() ;
;![]() ,
,![]() ;
;![]() ,
,![]() ) 3.7, 3, and 2 are in close agreement with the theoretical convergence rates 4, 3, 2. In this study for
) 3.7, 3, and 2 are in close agreement with the theoretical convergence rates 4, 3, 2. In this study for ![]() computations failed for discretizations coarser than 128 elements where equilibrium was not achieved.
computations failed for discretizations coarser than 128 elements where equilibrium was not achieved.
![]()
Figure 24. ![]() versus log(dofs) for solutions of class C1 (GM/WF, model problem 3, p = 3,
versus log(dofs) for solutions of class C1 (GM/WF, model problem 3, p = 3,![]() ).
).
7. A Posteriori Error Estimation and Computation
7.1. A Posteriori Error Estimation
A posteriori error estimation refers to estimation of errors in the computed solution. The primary purpose is to be able to devise some element-wise measures as well as in the whole discretization that quantify the errors in the computed solution as well as provide some guidance on the portions of the domain where the computed solution needs to be improved. Based on these measures one could design mesh refinement, p-level change, etc. strategies that result in the desired accuracy of the computed solution. This process of changing h, p, and possibly k based on measures estimated using the computed solution is referred to as adaptive process (i.e. we adapt h, p, and k as dictated by the current state of the solution and a posteriori error estimators or indicators).
During the development of finite element technology and even now, solutions of class ![]() have been used predominantly. The local approximations of class
have been used predominantly. The local approximations of class ![]() result in interelement discontinuity of the derivatives normal to the interelement boundaries. When the solutions of the BVPs are smooth, these interelement jumps in the derivatives are reduced upon h, p refinements and we say
result in interelement discontinuity of the derivatives normal to the interelement boundaries. When the solutions of the BVPs are smooth, these interelement jumps in the derivatives are reduced upon h, p refinements and we say ![]() solutions converge weakly to class
solutions converge weakly to class![]() . The a posteriori error estimations largely exploit the interelement discontinuities of the derivatives inherent in
. The a posteriori error estimations largely exploit the interelement discontinuities of the derivatives inherent in ![]() local approximations. We note the following.
local approximations. We note the following.
1) When the local approximations are considered in higher order spaces, the a posteriori error estimates used currently that are derived based on ![]() local approximations are meaningless as for higher order global differentiability local approximations the interelement jumps in the derivatives of the solutions used currently do not exist.
local approximations are meaningless as for higher order global differentiability local approximations the interelement jumps in the derivatives of the solutions used currently do not exist.
2) The ![]() local approximations can only be used in a system of first order differential equations to calculate the residuals and residual functionals over
local approximations can only be used in a system of first order differential equations to calculate the residuals and residual functionals over ![]() as well as over
as well as over![]() , but only in Lebesgue sense. For higher order BVPs such computations are not possible with local approximations of class
, but only in Lebesgue sense. For higher order BVPs such computations are not possible with local approximations of class![]() . Even though the residual functional over
. Even though the residual functional over ![]() and
and ![]() are true measures of how well the local approximation satisfies the BVP, the emphasis has been largely on a posteriori error estimation, primarily due to the insistence on the use of
are true measures of how well the local approximation satisfies the BVP, the emphasis has been largely on a posteriori error estimation, primarily due to the insistence on the use of ![]() local approximations.
local approximations.
3) Our view is that in a finite element computational framework the physics of the BVP must be preserved and in such a framework, once a finite element solution has been calculated, the computational framework must permit a posteriori computations of any desired measures otherwise the computational framework is deficient.
7.2. A Posteriori Error Computation
As mentioned in Section 7.1, the computational framework must be designed such that it permits a posteriori computations of all desired measures that are necessary and meaningful in adaptivity. Minimally conforming spaces play a crucial role in accomplishing this. We present details in the following. Let
![]() (150)
(150)
be a boundary value problem in which the differential operator may be self adjoint, non-self adjoint, or non- linear. Let ![]() be the highest order of the derivative of
be the highest order of the derivative of ![]() in (150). Let
in (150). Let ![]() and
and ![]() be approximations of
be approximations of ![]() over
over ![]() and
and![]() . The approximation
. The approximation ![]() is assumed to be computed from any of the methods of approximation in which the integral forms may be VC or VIC. Let
is assumed to be computed from any of the methods of approximation in which the integral forms may be VC or VIC. Let
![]() (151)
(151)
![]() (152)
(152)
The approximation space ![]() is minimally conforming ensuring that the integrals over
is minimally conforming ensuring that the integrals over ![]() are Riemann. Using (150) and (152), we can define residual functions
are Riemann. Using (150) and (152), we can define residual functions ![]()
![]() (153)
(153)
where n is the number of differential equations in (150). Let
![]() (154)
(154)
We define residual functionals I and ![]() over
over ![]() and
and ![]() by
by
![]() (155)
(155)
![]() (156)
(156)
Since![]() , we can write (using (155) and (156))
, we can write (using (155) and (156))
![]() (157)
(157)
If ![]() is the theoretical solution
is the theoretical solution ![]() then
then
![]() (158)
(158)
and
![]() (159)
(159)
over ![]() and each
and each![]() . Minimally conforming space
. Minimally conforming space ![]() ensures that integrals over
ensures that integrals over ![]() are Riemann, hence proximity of
are Riemann, hence proximity of ![]() to zero (theoretical value of functional I; that is,
to zero (theoretical value of functional I; that is,![]() ) is a measure of error in the solution
) is a measure of error in the solution ![]() over
over![]() . When
. When![]() ,
, ![]() , thus
, thus ![]() for each
for each ![]() in
in![]() , implying that differential Equation (150) are satisfied in the pointwise sense. Thus, the main steps in a posteriori error computation can be summarized in the following.
, implying that differential Equation (150) are satisfied in the pointwise sense. Thus, the main steps in a posteriori error computation can be summarized in the following.
1) Choose minimally conforming space ![]() thereby ensuring integrals over
thereby ensuring integrals over ![]() in Riemann sense.
in Riemann sense.
2) Regardless of the method of approximation to construct integral form in the finite element process, the following steps are possible and help in quantifying solution error. Calculate finite element solution ![]() and hence
and hence![]() .
.
3) Calculate![]() ,
, ![]() for each element e with domain
for each element e with domain ![]() of the discretization
of the discretization![]() .
.
4) Calculate ![]() for
for![]() .
.
5) When ![]() (
(![]() or lower),
or lower), ![]() is reasonably converged to
is reasonably converged to ![]() for the h, p, and k employed, hence no need for adaptive refinements.
for the h, p, and k employed, hence no need for adaptive refinements.
6) When![]() , we examine
, we examine ![]() values for individual elements of
values for individual elements of ![]() to determine which elements have
to determine which elements have ![]() values larger than a certain threshold value
values larger than a certain threshold value![]() . These elements can be considered for adaptive refinement (h or p or both) depending on the strategy adopted. Some of these are presented in the next section.
. These elements can be considered for adaptive refinement (h or p or both) depending on the strategy adopted. Some of these are presented in the next section.
7) In this approach, a posteriori error estimations derived and used presently (of little value in higher order spaces) are eliminated altogether.
8) Errors in the computed solution are quantified without the knowledge of theoretical solution and there is built-in adaptivity due to ![]() for individual elements. The elements with
for individual elements. The elements with ![]() values larger than a threshold value
values larger than a threshold value ![]() are candidates for refinement.
are candidates for refinement.
9) Adaptive processes based on ![]() values for elements of descretization
values for elements of descretization ![]() are presented in the next section.
are presented in the next section.
8. Summary and Conclusions
In this paper, we have considered a priori and a posteriori error estimations, a posteriori error computation, and convergence rates of the finite element computations for BVPs described by self-adjoint, non-self-adjoint, and nonlinear differential operators. Concepts of h-, p-, and k-versions and h-, p-, and k-convergences in finite element processes are presented and discussed. It is shown that a desired measure of error norm or residual functional versus degrees of freedom behavior has distinct features that can be classified as pre-asymptotic range, onset of asymptotic range, asymptotic range, onset of post-asymptotic range, and post-asymptotic range. The significance and importance of these ranges in finite element computations has been discussed and demonstrated through three model problems described by self adjoint, non-self adjoint, and non-linear differential operators.
The a priori estimates only hold in asymptotic range and their derivation in the currently published literature are only valid for self adjoint operators in GM/WF when functional ![]() is symmetric, thus GM/WF has best approximation property in B-norm. New work presented in this paper establishes correspondence between best approximation property of an integral form in some norm and the variational consistency of the integral form and demonstrates that when one exists the other is ensured. Thus, for establishing a priori error estimates, variational consistency becomes an essential property of the integral form. Of course best approximation property in some norm if it exists is equally good as best approximation property and variational consistency of integral form can not exist without each other, i.e. they co-exist. In case of GM/WF, VC integral form is possible for self adjoint operator and in case of LSP VC integral form is possible for all three classes of differential operators, hence a priori estimates for GM/WF for self adjoint operators and a priori estimates for LSP for all three classes of operators can be derived. The derivation of a priori error estimates presented in proposition 5.2 applies to GM/WF for self adjoint operators and in case of LSP for all three classes of operators as well as any other integral form resulting from a chosen method of approximation as long as the integral form is VC. Numerical studies for the model problems containing the three classes of operators confirm that when the integral form is VC, same a priori estimates and convergence rates hold. Thus, for the first time we have a priori error estimates for non-self adjoint and non-linear differential operators. Extensive numerical studies are presented for various p and k values for uniform h-refinements demonstrating that the theoretically derived convergence rates in a priori estimates are always in agreement with calculated values when the integral forms are VC. The a priori error estimates derived here also hold for 2D and 3D BVPs as long as the integral forms in these BVPs are variationally consistent. This can be confirmed numerically and is in agreement with published literature for self adjoint operators.
is symmetric, thus GM/WF has best approximation property in B-norm. New work presented in this paper establishes correspondence between best approximation property of an integral form in some norm and the variational consistency of the integral form and demonstrates that when one exists the other is ensured. Thus, for establishing a priori error estimates, variational consistency becomes an essential property of the integral form. Of course best approximation property in some norm if it exists is equally good as best approximation property and variational consistency of integral form can not exist without each other, i.e. they co-exist. In case of GM/WF, VC integral form is possible for self adjoint operator and in case of LSP VC integral form is possible for all three classes of differential operators, hence a priori estimates for GM/WF for self adjoint operators and a priori estimates for LSP for all three classes of operators can be derived. The derivation of a priori error estimates presented in proposition 5.2 applies to GM/WF for self adjoint operators and in case of LSP for all three classes of operators as well as any other integral form resulting from a chosen method of approximation as long as the integral form is VC. Numerical studies for the model problems containing the three classes of operators confirm that when the integral form is VC, same a priori estimates and convergence rates hold. Thus, for the first time we have a priori error estimates for non-self adjoint and non-linear differential operators. Extensive numerical studies are presented for various p and k values for uniform h-refinements demonstrating that the theoretically derived convergence rates in a priori estimates are always in agreement with calculated values when the integral forms are VC. The a priori error estimates derived here also hold for 2D and 3D BVPs as long as the integral forms in these BVPs are variationally consistent. This can be confirmed numerically and is in agreement with published literature for self adjoint operators.
A posteriori error estimation based on the work presented here is viewed unnecessary when the approximation spaces are minimally conforming or of orders higher than minimally conforming due to the fact that when using such spaces a posteriori error computations of any desired quantity (for example ![]() and I) that can help guide adaptivity is possible.
and I) that can help guide adaptivity is possible. ![]() residual values for elements of
residual values for elements of ![]() are shown to be a perfect choice for adaptivity.
are shown to be a perfect choice for adaptivity.
In short, VC integral form permits derivation of a priori error estimates and determination of convergence rates for all three classes of differential operators and use of minimally conforming spaces make a posteriori error estimation unnecessary and permit determination of desired a posteriori measures (such as ![]() and I) that can be used to quantify errors in the currently computed solution and to design adaptive processes (presented in a followup paper). The same estimates and convergence rates hold for 2D and 3D BVPs when the integral forms are VC. The details are somewhat involved and have been presented in published literature for self-adjoint operators.
and I) that can be used to quantify errors in the currently computed solution and to design adaptive processes (presented in a followup paper). The same estimates and convergence rates hold for 2D and 3D BVPs when the integral forms are VC. The details are somewhat involved and have been presented in published literature for self-adjoint operators.
Acknowledgments
The first and third authors are grateful for the support provided by their endowed professorships during the course of this research. The computational infrastructure provided by the Computational Mechanics Laboratory (CML) of the Mechanical Engineering department of the University of Kansas is gratefully acknowledged. The financial support provided to the second author by the Naval Air Warfare Center is greatly appreciated.