Incompleted Field Strength Calculation of the Potential Term Adopted from Landau-Ginzberg Theory Applied in Particle Physics ()
Received 15 March 2015; accepted 22 July 2016; published 25 July 2016

1. Introduction
There is a widely used potential term in superconductivity, mean field theory, Landau-Ginzberg theory applied in spontaneous symmetry breaking of particle physics [instead of spontaneous the term instantaneous can also be used but symmetry breaking takes time from fractions of a second to hours in condensed matter physics]. Here calculation of the field strength coupling is completed of the potential term for the theory of particle physics. Similar steps are applicable in the theory of condensed matter physics as well. What is missing in Landau- Ginzberg theory is also getting corrected.
Maxwell formulated the theory of electromagnetism unifying electricity and magnetism and predicted the value of light speed. But photon was a massless particle. Klien, Gorden and Proca [1] advanced the theory for massive quantas. Landau and Ginzberg formulated the theory of phase transition in condensed matter physics. J. Goldstone [2] discussed field theories with superconductor solutions. With Weinberg and Salam, Goldstone [3] discussed broken symmetries. P. W. Higgs [4] adopted form of the potential from Landau and Ginzberg & field theory from Goldstone applied in symmetry breaking of particle physics and discussed how quantas can acquire mass in the broken symmetry which became popular as Higgs mechanism. Weinberg and Salam formulated the electro-weak theory unifying weak and electromagnetic interactions. They predicted values of W and Z bosons theoretically which are massive quantas and Higgs played a valuable role in the mass generation. It was said that W and Z bosons became massive by eating Higgs. Itself is sufficient to say Higgs mass is less than W and Z boson masses, not higher average values of CERN experiments of year 2012 which are logically ruled out. But neither P. W. Higgs nor S. Weinberg and A. Salam could provide a theoretical value for Higgs quanta in both of their versions of the theory. This is where the present author has played a key role. The most important breakthrough is the completion of field strength calculation of the potential term, the missing part of Higgs, Weinberg and Salam theories and prediction of Higgs quanta mass by the present new author. In electrostatics field strength is square of the charge of the electron in Coulomb Potential; if Higgs had studied this field strength coming from inverse square law of Coulomb he would not have missed the evaluation of the coupling in his noted theory on massive quantas. Higgs and Weinberg’s formulation of the theory is elegant but both could not come to the logical conclusion with Salam; their undetermined parameter λ (in Weinberg’s version it is h) is simply of the order of e2, the square of the charge of the electron except a simple numerical factor.
2. Starting with Lagrangian Density of the Form
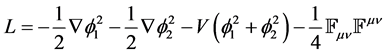
where
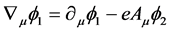
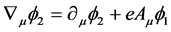
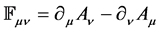
In which two real scalar fields 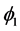 and
and 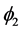 & real vector field
& real vector field 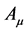 are interacting and it is a model used by Goldstone. Metric is taken as − + + + Simultaneous gauge transformations are to be applied on
are interacting and it is a model used by Goldstone. Metric is taken as − + + + Simultaneous gauge transformations are to be applied on 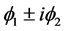 and on
and on
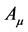 ,
, 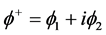 , complex conjugate of it
, complex conjugate of it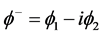 ,
, 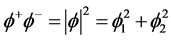 ,
, 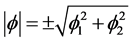 By Taylor- Maclaurin expansion
By Taylor- Maclaurin expansion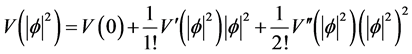 . Suppose that
. Suppose that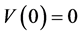 ,
, ![]() ,
, ![]() the condition for minima. Take
the condition for minima. Take ![]() to be evaluated by calculation the field strength of interacting potential. Then
to be evaluated by calculation the field strength of interacting potential. Then ![]() at the minima. Now at minima let the potential be slightly perturbed by it’ s continuous rotational symmetry with the selection
at the minima. Now at minima let the potential be slightly perturbed by it’ s continuous rotational symmetry with the selection![]() ,
, ![]() at
at![]() . Then
. Then![]() ,
, ![]() ,
, ![]() what is said be
what is said be ![]() symmetry.
symmetry.![]() ,
,![]() . Now
. Now ![]() symmetry is subjected to
symmetry is subjected to
be broken at the selected values in the way![]() , & simultaneous gauge transformations are subjected to be perturbed as follows,
, & simultaneous gauge transformations are subjected to be perturbed as follows,
![]()
![]()
![]()
Euler-Lagrange’s equations of motion
![]()
In the limit when ![]() the vacuum solution
the vacuum solution ![]() considering (1) only oscillations around 0.
considering (1) only oscillations around 0.
![]()
In the limit when ![]() the vacuum solution
the vacuum solution ![]() considering only oscilla-
considering only oscilla-
tions around ![]() the equation
the equation ![]() describes waves whose quanta (2) has bare
describes waves whose quanta (2) has bare
mass![]() ,
, ![]() and the speed of light propagation
and the speed of light propagation ![]() the speed of light for massless quanta which has zero bare mass that Goldstone was discussing. The important point is massive quanta travel with a lesser light speed than massless quanta. Gravitons and Neutrinos are examples for massive quanta s having lesser light speed than for massless photons.
the speed of light for massless quanta which has zero bare mass that Goldstone was discussing. The important point is massive quanta travel with a lesser light speed than massless quanta. Gravitons and Neutrinos are examples for massive quanta s having lesser light speed than for massless photons. ![]() are the coordinates of the minima on complex mathematical plane .There are two such points.
are the coordinates of the minima on complex mathematical plane .There are two such points.
![]() within the limit
within the limit ![]() and
and ![]()
![]()
![]()
From Equation (1),
![]()
describes vector waves whose quanta have bare mass ![]()
![]() (3)
(3)
the vacuum solution
![]()
and scalar & vector part both are component of the same tensor describing same massive quanta such as graviton or neutrinos propagating with the lesser light speed than massless photon light. So that mass of the quanta
derived from two different ways have common value. Therefore![]() ,
, ![]() , so that
, so that![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() is the first constant of integration
is the first constant of integration ![]()
![]() the second constant of integration
the second constant of integration![]() ,
, ![]() ,
, ![]() at
at![]() ,
, ![]() ,
, ![]() , where m is the mass of the quanta prop-
, where m is the mass of the quanta prop-
agating with slow light speed the new light that illuminate the entire universe namely graviton light & neutrino light. The propagation speed of new light ![]() the photon light of the massless quanta. The example for graviton light is the moon light.
the photon light of the massless quanta. The example for graviton light is the moon light.
![]()
and the curve cut the imaginary axis of the complex mathematical plane at those points and at ![]() it touch
it touch
the imaginary axis at an apparent maxima ![]() at
at ![]() the potential curve
the potential curve
has two minima s and ![]() it acquire zero value. It leads to infinity at infinite limit in both directional parities
it acquire zero value. It leads to infinity at infinite limit in both directional parities
![]()
![]()
where ![]() and m is the mass of the quanta traveling with slow speed of light.
and m is the mass of the quanta traveling with slow speed of light.
3. In Particle Physics Related with Electro-Weak Unification
![]()
and reconfirmed in the neighborhood of this peak value by compact muon solenoid in European accelerator for particle physics at Geneva in the Alps Snow Mountain Range in an enchanting picturesque. Higgs Boson is identified as relativistically accelerated heavy graviton and W and Z bosons are identified as relativistic ally accelerated heavy neutrinos & spin is identified as energy scale dependent physical quantity in this analysis. Further
![]()
![]()
Multiplying the above relation by factor![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
,
![]() the mass of the Higgs Boson as confirmed by
the mass of the Higgs Boson as confirmed by
CMS experiment at this peak neighborhood at Geneva in 2012. They have confirmed it 1991 [6] LEP:L3, Delphi, Opal, Aleph experiments also. The present author here provides the important pieces of work with proofs merited missed by Salam and Weinberg in their original papers of electroweak unification where Higgs can feel comfort after long delay. Higgs mass is the perpendicular drawn from the vertex at the right angle on the opposite side hypotenuse of the mass triangle corresponding to coupling constants of electroweak unification theory. g correspond to the strength of coupling of weak interaction and g' corresponds to the strength of coupling of electromagnetic interaction. e the charge of electron and ![]() the fine structure constant & θW the Weinberg angle, c the speed of light in vacuum, ε0 the permittivity of vacuum, h the plank constant,
the fine structure constant & θW the Weinberg angle, c the speed of light in vacuum, ε0 the permittivity of vacuum, h the plank constant, ![]() the Fermi coupling constant, MZ the mass of Z boson, MW the mass of W boson, MH the mass of Higgs boson, π the common ratio of circumference to diameter of all circles.
the Fermi coupling constant, MZ the mass of Z boson, MW the mass of W boson, MH the mass of Higgs boson, π the common ratio of circumference to diameter of all circles.
4. Conclusions
Field strength of the potential term adopted by P.W. Higgs from Landau-Ginzberg theory applied in particle physics has been theoretically calculated by present author in both Higgs and Weinberg-Salam versions of the theory. Meanwhile field strength was kept undetermined by Higgs, Weinberg-Salam following the way it was first formulated by Landau and Ginzberg. They all expected that it is a phenomenological parameter whose value can be given by experimental basis only. But it is worth to mention that it is hard to do experiments when there is no theoretical expression for this parameter then question arises―what is there to measure when it is not well defined. The important difference between former authors and our self is that present author provides a theoretical prediction for the field strength and Higgs mass which are fully consistent with latest experimental values. Experimenters have to adopt this new version with upgrading and calibrating their instruments.
In this work very important points missed by P. W. Higgs [4] in his first analysis of the Goldstone model were presented. Higgs [4] would not have missed the derivation of lambda coefficient at his time if he had carefully studied Klein-Gordon and Proca equations as scalar and vector component of one tensor corresponding to one massive quanta travelling with slow light speed than massless photon light.
But this point is apparent in the paper written by Kibble [4] and his collaborators at Imperial College in London at their time in which same ![]() is appearing for scalar and vector part of the boson. Even S. Weinberg and A. Salam have missed the point at their time. But E. Witten [5] , J. Ellis [6] have come nearby. A. Lahiri [7] also has similar settings. The dot peak value of 2012 CERN experiments is the Higgs mass1. Very clear picture of what was missing is very much apparent in the review of Julius Runninger [8] .
is appearing for scalar and vector part of the boson. Even S. Weinberg and A. Salam have missed the point at their time. But E. Witten [5] , J. Ellis [6] have come nearby. A. Lahiri [7] also has similar settings. The dot peak value of 2012 CERN experiments is the Higgs mass1. Very clear picture of what was missing is very much apparent in the review of Julius Runninger [8] .
Acknowledgements
This work was inspired by James Clerk Maxwell [8] , Klein-Gordon [8] and A. Proca [8] , and was assisted by W. Nadun, Susitha. S, A. C. Ranjith De Alwis at address No. 299, Galle Road, Gorakana. The Golden Lanka [Tamma Panni] is the Historic Name of Lanka the present author [alternative E-mail: dealwis_a@yahoo.com] is staying.