Connections between the Specific Absorption Rate and the Local Temperature ()
Received 12 April 2016; accepted 27 June 2016; published 30 June 2016

1. Introduction
Curative and palliative applications of hyperthermia are an ancient practice. Various energy sources may be used for local heating or for completely heating the entire body:
・ Conductive (like hot bath, sauna, etc.)
・ Convective (like extracorporeal blood heating, intraperitoneal hyperthermia, washing body-cavities by hot electrolyte, etc.)
・ Radiative (like Sun-bath, artificial non-ionising and ionising electromagnetic radiations, mechanical [usually ultrasound] vibrations, etc.)
The specific absorption rate (SAR) measures the absorbed power from outside energy sources; irrespective of the kind of source, only the energy flow has to be counted. This incoming energy makes changes directly or indirectly (triggering biological mechanisms) in the targeted tissues or the whole body.
Heat and temperature are completely different categories. Heat is energy, which is necessary to produce temperature. Naturally, when we have a large object, it needs more heat to reach a given temperature than a small object that is heated on the same temperature value. Let us use a simple example: the body temperature of healthy humans is fairly constant (deviation is less than ±1˚C, approx. 0.3%), while the human energy consumption (heat equivalent) varies in a wide range individually (deviation can be more than 100%). The same individual could have very hectic energy intake depending on complex conditions (deviation can be more than 50%), with no change in body temperature. Without a notable change in the temperature, we are able to pump energy (heat), mass, volume, entropy (information), etc. into the body. These processes are characterised by extensive thermodynamic parameters (heat, mass, volume, etc.) identifying the processes quantitatively. Intensive parameters (like temperature, pressure, chemical potential etc.) distinguish the thermodynamic state, describing the actual quality (momentary equilibrium) of the targeted system. Gradients of these intensive parameters are the driving forces of the flow of extensive ones. The flow of the extensive parameters changes the equilibrium, therefore redefining the intensive parameters in the system. Let us study a simple steam engine: the applied energy (heat) heats up the system, causing its temperature to rise. However, the engine starts to work only when the water temperature has reached a definite value. From this moment, the temperature remains stable, the engine starts to work, and the pumped-in heat is converted to useful mechanical energies, which is the aim of the engine application. If we stop taking away the mechanical energy (block the engine), but the energy intake remains the same, then the excess energy starts to increase the temperature.
The heat energy of an object (called internal energy) is proportional to its mass, while the temperature is independent from the size of the object. The complete pumped in energy may be absorbed like heat or a working power, which changes the chemical state or other energy-dependent processes in the target. The energy intake could be various, depending on the target’s structure and internal properties. Among the many energy exchange forms, the most important are:
・ mechanical energy (p∆V, pressure [p] multiplied by the change of volume, [∆V]);
・ chemical energy (μ∆N, the chemical potential [μ] multiplied by the change of the number of participating compounds, [∆N]);
・ electric energy (E∆P, the electric field [E] multiplied by the change of polarisation, [∆P]);
・ electric current energy (q∆V, the electric charge [q] multiplied by the change of the voltage [∆V]);
・ magnetic energy (H∆M, the magnetic field [H] multiplied by the change of magnetic moment, [∆M]);
・ simple heat energy (T∆S, the temperature [T] multiplied by the change of entropy, [∆S]).
Hence, altogether, the internal energy is a sum of all of the works:
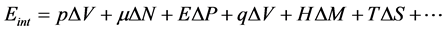 (1)
(1)
These changes are not independent, and are well interconnected with each other (for example the growing temperature dilates the object, which performs mechanical work). The interconnections are linear close to equilibrium [1] [2] . The terms which have no temperature component (fields, mechanical pressure, chemical changes) could probably be called “non-thermal” effects. However, this is false.
According to the second law of thermodynamics, real processes always have dissipation. The absorbed energy is not able to be transformed completely into useful energy, like breaking DNA strands by ionising radiation. The maximum fraction of the absorbed energy which can be transformed is called exergy. Exergy is the energy that is available to be used. The remaining part is called anergy, and this corresponds to waste heat [3] . A simple graphical explanation of exergy is shown in Figure 1 .
When the surroundings are much larger than the target inside, exergy is the potential of a system to cause a change, as it achieves equilibrium with its environment [4] . Energy never “vanishes” in any process; it changes from one form to another. However, in contrast, in the process when the system and surroundings reach equilibrium, the exergy gradually becomes zero, and the energy is depleted.
As a consequence, no effect could happen without energy dissipation, which is heat and may change the local (maybe in the micro- or nano-range environment) temperature.
The absorbed specific energy (ASE; ASE = SAR*time) is the source of the desired changes or at least triggers various processes in the complex living matter. In medical practice, ionising radiation uses the energy absorption for dosing, which counts the duration of the power absorption too [Gy (=J/kg)]. Here, the ionisation has a certain distortion in the DNA, which is the goal of radiation in oncology. The ionising rate is the main result, and the developed temperature is the only unwanted side effect. In case of non-ionising radiation, the same characterisation is used for completely opposite goals. There, the direct interest is the temperature increase, and the excitation processes and energy consumptions other than temperature increases are neglected (Figure 2 ).
In the case of ionising radiation processes, the emphasis is on exergy, while in hyperthermia it is the opposite: the emphasis is on anergy, on the “purely heating” process. This goal overemphasises the role of temperature. In principle, hyperthermia uses the heat energy (anergy) to destroy the malignant cells/tissue, and to reach the definite aim of the treatment. Unfortunately, this goal is often exchanged with the demand of the increase of the temperature, using the high temperature as a direct aim of the treatment.
Elementary physiological reactions triggered by the temperature increase:
・ increased metabolic rate, which adds heat to the external energy intake,
・ heat-sinks (mainly the blood-flow) effectively cooling the locally heated volume, trying to re-establish thermal homeostasis.
The metabolic rate (M) determines the heat liberated by the given tissues in the unit volume. There, 60% of the daily energy expenditure is used by the metabolism {basal metabolic rate (BMR)} in humans [5] . The constrained temperature rise increases the metabolic rate (MR(T)) exponentially [6] . A 7˚C increase in temperature doubles the metabolic rate. This effect significantly modifies the heat-distribution, which is a positive feedback mechanism of the well-focused hyperthermia. Fundamentally, the tumour has a higher metabolic rate, which depends on the tumour-growth-rate [7] [8] .
![]()
Figure 1. Relation of the energy and its parts the exergy (work for definite use) and anergy (dissipative energy, which cannot be turned for work).
![]()
Figure 2. The energy use in cases of ionizing and non-ionizing radiation. The ionizing radiation destroys the integrity of DNA (exergy) and only a small heat (anergy) is produced, while the non-ionizing emphasizes the heating (anergy) and the work of the electromagnetic field (exergy) is much less.
The heat-sink mechanism (controlling the thermal homeostasis) is much more complex. The SAR increases the temperature, but due to the cooling of the physiologically regulated blood-stream, this heating mechanism is much less effective than without blood cooling. Consequently the temperature is definitely lower than in a regular phantom without blood-stream, even if the phantom material fits well to the targeted real tissues. The blood- stream has a central role to maintain homeostasis, and regulates the heat exchange to ensure the proper functional conditions of the targeted area. The blood-stream tries to compensate the overheating by intensive perfusion and regulation of the flow-capacity of the vessels, by the intensive vasodilatation of arteries.
Oncological applications of hyperthermia are among the emerging therapies with heat treatments. The oncological applications are very complex due to the malignant situation. The challenge is connected to the goal of the oncological treatment: destroy the tumour directly or indirectly, but to ensure that it is complete if possible. The direct tumour-distortion is typical in the ablation techniques, when the high temperature in short duration burns out the volume where the very concentrated energy is effective. The SAR value in ablation is high (range of 10 - 100 kW/kg [9] ), and as high in the nanoparticle heating as well [10] . The majority of the hyperthermia applications presently have double focus: local, tumour-targeting energy delivery or heating the whole body. Here, the typical SAR values are much lower than in ablation techniques, ranging three orders of magnitudes less: 10 - 100 W/kg. The SAR is the tool used to accomplish the desired goal to destroy the tumour.
There are two misuses of the hyperthermia categories. There is frequent use of the term “fever-therapy” and “whole-body hyperthermia” (WBH) as synonyms. This is a false concept, however, because fever (and fever therapy) shifts the set-point of body temperature in the hypothalamus, and the body develops the fever itself. In whole body hyperthermia, the set-point is fixed; the thermal homeostasis works against constrains outside heating. The other misuse of the concept is the mix of local-regional hyperthermia with WBH, concentrating on the temperature which is achieved by these methods. However, the two modes of heating are completely different. The peripheral blood heats up the body in the WBH approach, and the tumour is heated up by this hot blood (Figure 3 ).
In the local-regional hyperthermia, the blood remains at body-temperature while the target is focused to heat. In this case, the blood cools the tumour, causing completely opposite heat-flow than in WBH (Figure 4 ).
In the following, we deal with local-regional hyperthermia only; the whole-body treatment is out of our scope.
![]()
Figure 3. The opposite heating role of the loco-regional (a) and systemic, whole-body (b) methods. The dense capillary-supply (redrawn from human MDA MB231 breast cancer cell tumour grown as a xenograft in a female nude mouse, University of Potsdam) in the case of loco-regional heating is a heat-sink, which cools-down the otherwise heated area, while the systemic heating heats up its environment in by same dense capillary supply.
![]()
Figure 4. The local heating pumps SAR into the target but the blood-flow tries to keep the thermal homeostasis of the body trying to cool down the overheated lesion.
The real challenge of local hyperthermia is: to focus the energy on the target, select the malignant cells (as microscopically as possible), and distinguish them from their healthy counterparts. Two definite selection mechanisms force the energy-delivery to the malignant target: blood-perfusion regulation, and bio-impedance.
The variation of the requested SAR to keep a given temperature naturally means that at a constant SAR, the temperature increase will not be constant.
2. Methods
Three phenomena have to be used as a method to study the interconnection of SAR and the developed temperature:
・ Thermal exchanges and dynamics.
・ Penetration of the incident energy.
・ Blood perfusion (BP), vasodilatation/vasocontraction during hyperthermia.
2.1. Thermal Exchanges and Dynamics
The “thermal” process is defined by the Arrhenius principle [11] [12] . The reaction rate of any reaction caused by a temperature change depends on the exponential function of the inverse absolute temperature (T, measured in Kelvins [K]). This simple relation is the consequence of the ratio of the activation energy (Ea) [J/mol], to the thermal one (RT), R (universal gas-constant, R = k × 6 ´ 1023 ≈ 8.3 J/K/mol) by growing the thermal energy, the
reaction (going over Ea) is more likely. Hence, the probability of a given reaction depends on the 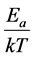 ratio,
ratio,
which determines the reaction rate (Rr), by a normalisation pre-exponential factor (A):
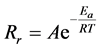 (2)
(2)
The value of A pre-exponential factor depends on the distribution of velocity (kinetic energy), on the collision frequency and on the reaction cross-section. It depends on the temperature by its square-root. In practical applications, we apply the logarithm of the Equation (2):
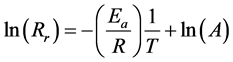 (3)
(3)
Equation (3) is suitable to determine the activation energy of a particular process if we measure the (1/T) dependence of the logarithm of the chemical reaction rate.
The Rr rate constant is characteristic for the actual reaction-rate, with two states “State 1” and “State 2”, with [C1], [C2] and E1, E2 concentrations and activation energies. If they are the two sides a reaction equation, Figure 5 , then:
![]()
Figure 5. The reaction energy-schematics between “State 1” (initial) and “State 2” (final).
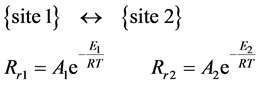 (4)
(4)
In equilibrium stage, the rate of conversion {State 1} → {State 2} is equally balanced by the reverse {State 1} ← {State 2} reaction, so:
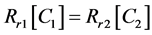 (5)
(5)
Hence, the reaction rate in equilibrium is:
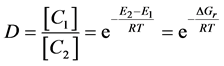 (6)
(6)
We consider a reaction to be “thermal” when the Arrhenius plot is applicable.
The definite change in activation energy is plausible in all of the phase transitions [13] , when the material is transformed from one to the other state. The initial and final stages have different chemical bonds, which characterise the phase itself. At least in this point, when the chemical-transformation occurs, the Arrhenius-line (the 1/T-function) will change its slope. The phase-transition-like changes could be observed by the breaking point in the plot (Figure 6 ). The actual breaking point depends not only on the heating process; it changes by the applied chemotherapy [14] , and even has an opposite change in the Ea in case of oxaliplatin [15] , as well as depending on the prehistory and dynamics of treatment [16] - [20] . This means that the kink, which is the basis of the presently used dose, is not definite at all.
To very roughly calculate the gain of temperature, over estimating the heat losses, we can start with the basic equation of the elementary thermodynamics:
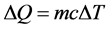 (7)
(7)
where the DQ is the absorbed anergy, m is the heated mass, c is its specific heat and DT is the temperature gain.
The initial body temperature, considering the density as homogeneous and unit value; derived from (7):
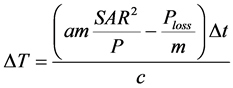 (8)
(8)
Assume a large tumour, with a mass of m = 3 kg (c = 4183 Ws/kg/K, the density of the tumour is 1.1 kg/dm3)
and heating conditions are forwarded power Pforw =150 W, 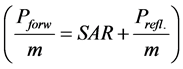 , (Prefl. is the reflected power).
, (Prefl. is the reflected power).
![]()
Figure 6. The reaction energy-schematics between “State 1” (initial) and “State 2” (final).
Consider the efficacy of tumour selection as a = 30% and the constant energy loss of the tumour is 5 kW/m3. (This last is huge overestimation, because the blood-flow power-loss is about 3 kW/m3, and its temperature dependence as well as the metabolic extra-power is not considered. Here we have taken account the specific loss of
power![]() , measured in W/m3). Using these conditions we have 45˚C of tumor temperature after Dt = 60
, measured in W/m3). Using these conditions we have 45˚C of tumor temperature after Dt = 60
minutes of treatment time. (The refinement of this estimation is published elsewhere [18] ). Consequently, relatively low energy could be enough to reach the desired treatment conditions.
![]() (9)
(9)
2.2. Penetration of the Incident Energy
The penetration depth decides the gradient of the SAR in the target. It sharply and inversely depends on the wavelength [21] in the RF-radiation process and could be modified by the wave-source symmetry [22] . Also, the absolute value of the absorbed energy in a definite depth is linearly proportional with the incident energy. The planar-waves at the applied relatively low frequency generated by plate antennas penetrate into the body by 14 - 20 cm [23] [24] . (The penetration is defined by the depth, where the energy intensity is about 36% of the incidence-beam). However, in the case of the strict RF-current energy-transfer, the Joule-heat and the delivered direct energy will dominate the process. The “penetration” of the current is the whole target in capacitive coupling (current flows between the electrodes), but the current density changes by depth, and determined the actual energy-delivery (Figure 7 ). This is crucial for the control and quality-reproducibility of the treatment [25] .
Most hyperthermia effects have a wider interval of the active energy for desired changes. Consequently, it is possible that less than 36% of the initial energy is sufficient for the desired active effects, so the active depth is more than the technical penetration (Figure 8 ). Additionally, the lower energy range in depth may optimise the effect, which is more effective in weaker SAR ranges [26] .
2.3. Blood Perfusion (BP), Vasodilatation/Vasocontraction during the Hyperthermia
The difference between the absolute blood-flows of the tumour and healthy tissue is recognised [27] - [31] , as well as the relative change of the blood-flow by temperature, is well described in other works [32] [33] . The microcirculation of tumour and its changes by hyperthermia are studied in detail [34] - [40] [48] [55] . The physiologic effects connected to the blood-flow are considered important and have also been studied in detail [41] - [44] [54] . The central fact is: the change in blood-flow is temperature-dependent and has a turning point for tumour- lesions. Detailed reviews and discussions on the latest results of tumour-blood-flow affecting the applied temperature have recently been published [45] - [47] .
![]()
Figure 7. The penetration of the energy in the impedance-coupled system differs from the plane-wave penetration of the general capacitive coupling. The current flows through the whole cross-section (from one electrode to the other), but only the current density changes. This change depends on the inhomogeneity of the body part being treated, so the density distribution is personal.
![]()
Figure 8. The desired action (distortion of malignant cells by any kind of cell killing) certainly differs from the penetration depths. It is a wide interval, which could only be defined by its limits: the upper limit when the burn is toxic, and the lower limit, the energy, which is necessary for the signal triggering of apoptosis.
An effective vascular response to heating could be observed [48] [49] , which over a tumour-specific threshold (from about 38˚C), differentiates between the malignant-tumour and normal/benign tissues [45] - [47] . It has been shown that an increase in temperature can cause vasoconstriction in certain tumours leading to decreased BP and heat conduction [48] - [50] , while causing vasodilatation in the healthy tissues leading to increased relative BP and heat conduction in this region [31] [51] . However, BP of the tumour relative to the surrounding healthy tissue is always lower [54] , providing an effective heat trap [52] [53] . This phenomenon is only effective in the neo-vascularised area, where the epithelium of new vessels differs from the normal [54] . Consequently, this is emphasised in large tumours, where the core is already necrotised, and has no blood flow at all. A quantitative analysis [55] showed the blood-flow in characteristic tissues (Figure 9 ), varying by temperature.
Changes in blood-flow are summarised in Table 1 . The change affects not only the temperature itself, but also the complementary applied chemo- and/or radiotherapy efficacy. The blood-perfusion is mandatory for drug- delivery, but the oxygen content defines the efficacy of the radiotherapy.
As a consequence, both the frequently applied conventional complementary therapies are far from independent form this perfusion issue (see Table 2). This specialty of the blood-flow has to be considered for complementary chemo- and radio-potentiating (or resensitising).
The deviation (selection) of the tumour blood-flow starts at just above 38°C in the model calculation [58] (Figure 10 ).
From these studies, we learned the relative blood-flow changes in healthy and in tumour tissues are parallel below the specific threshold, starting at 38˚C. The maximal threshold value in the literature is 42.5˚C. The limit corresponds well with the believed cellular phase transition observed at around 42.5˚C [56] . This however surprisingly accurately fits to experimental results of in vitro studies by Arrhenius plot [57] [58] . However, above this limit the blood-flow suddenly splits, the tumour and the healthy tissue are characteristically down- and up-regulated, respectively. The blood-flow (BF) further increases in healthy tissue, while contrary, in tumour- tissue it becomes down-regulated.
![]()
Figure 9. Quantitative changes of the blood-flow by temperature increase in (a) muscle; (b) adipose tissue; and (c) the tumour lesion.
![]()
Table 1. Blood-flow changes and its consequences below and above the actual threshold for healthy and tumour tissues. Note that over the threshold, the tumour has the opposite direction of development compared to below it.
![]()
Table 2. The potentiating differences of oncothermia under- and over-threshold conditions. Note that over the threshold the tumour has a worse situation than below it.
The blood flow in solid tumours depends on the tumour-weight by negative logarithmic function [59] . As a consequence, large tumours have lower blood-flow which minimises the development of the tumour mass, and results in the overall heating of the tumour.
Microscopically, the capillary vessels have a special role in heat delivery. The blood delivered by capillaries is the source of oxygen, so the oxygenation of the tissue is tightly connected to capillary blood-perfusion (Figure 11 ) [60] [61] . It is definitely modified by hyperthermia. Due to cooling by arteries, the heat-flow in this microscopic volume is in the opposite direction to the flow of metabolic species, despite the homogeneous SAR.
The characteristic oxygen-distribution (see Figure 11) is effective around a capillary any time; its existence is irrespective of the hyperthermia applications, as only its actual value could differ in therapeutically effective periods. The gradient direction of nutrients will not change by the applied heat; only the gradient value will be modified. However, the heat flow is opposite and directs to the arteriole, because the blood cools. It is not only the character of the oxygenation, but all of the diffusion-derived phenomena (pH-distribution, drug-distribution, and in general all the chemical species delivered in- or out by blood) behave in the same non-homogeneous character, despite the homogeneous distribution of SAR over the volume (Figure 12 ).
The gradient could be guessed in equilibrium to 50 μm [62] . According to the direct measurements [63] [64] , and from the density experiments [65] , the inter-capillary distance is in the same range, so the dynamic equilibrium is effective for the whole mass of the living tumour (necrotic part is excluded).
Detailed analysis was given as early as 1959 on heat-regulation [66] , showing the sudden increase of the con- ductance of healthy tissues by the internal temperature change at the turning point of 36.7˚C by blood-flow, changing from 21 W/K to 150 W/K (seven-fold) at 37.3˚C. This huge heat-conducting capability must not be ignored by heating of the tissues.
![]()
Figure 10. Comparison of blood-flow by different tissues: (a) absolute values, (b) relative values.
![]()
Figure 11. The microscopic difference in the vicinity of a capillary vessel [64] . The heat-flow is in the opposite direction to the flow of nutrients and oxygen.
3. Results
SAR values show the derivative of the temperature development just in the start [67] [68] :
![]() (10)
(10)
However, this situation is only at the start of heating, when the blood-flow does not have active feedback to cool, and the conductive and convective heat transfers are also negligible. When the heat-transfer parameters grow to the same power, that which is kept constant is distributed to larger and larger volumes, heating more and more mass in the sample; the temperature change decreases, and in the case of stationary equilibrium, the temperature becomes constant at a constant SAR.
The thermal processes modify the heat-distribution; consequently, the SAR will not be “adiabatic” (Figure 13 ).
![]()
Figure 12. Schematics of the main physiologic parameters in the thermodynamic equilibrium of the hyperthermia in the microscopic range at homogeneous SAR in the volume. The values are in arbitrary units; only the trends [66] are shown so a relative comparison of the values is impossible. Locally, the temperature may be higher than the systemic physiological limit (42˚C).
![]()
Figure 13. The initial slope is the “adiabatic” SAR. When the material is heterogeneous, the heat-diffusion starts and the linear dependence bends. After the feedback reaction time of the thermal homeostasis, the intensive cooling of the blood starts which further bends the curve.
The saturation value in dynamic feedback mechanism [69]
![]() (11)
(11)
Using the average value of BP: wb = 3.5 kW/m3/K = 3.5 W/ℓ/K, we get numerically:
![]() (12)
(12)
where Tb is the actual temperature of the blood (body). In the simplest case of only heating, SAR is completely
proportional to the temperature increase, with no change of the slope of![]() . In this case, nothing else happens
. In this case, nothing else happens
in the heated object, only the average energy increases; there is no exergy for special distortion work, as all of the energy is purely heat (anergy), which is distributed equally in the target.
However, this picture is oversimplified. We have no idea about the effectively heated mass at the start, due to the non-homogeneous absorption (exponential decay by depth) of the electromagnetic energy. The increase in the mass which we heat is only relative. It is even possible that the stationary state is not the saturated maximal temperature, but lowered considerably by the gradual increase in thermal homeostatic feedback; the blood cools the tissue to close to its overall thermal equilibrium (Figure 14 ).
Counting the threshold, the vasocontraction changes the situation even in homogeneous heating processes. The growing SAR linearly increases the temperature but at the threshold, the lower SAR would have the same or higher temperature, which goes back to linear dependence over the threshold with a different slope (Figure 15 ).
When the cellular distortion happens, it uses part of the SAR. Consequently, the temperature rise will be moderated by the missing energy, which is used for cellular effects (Figure 16 ).
Due to the time delay of the physiological feedback and the non-linear temperature dependence of the blood- flow, together with the negative slope of the SAR vs. temperature near the threshold point (see Figure 15(b)), the heat-up and cool-down processes have jumps at certain SAR values, which are different in the two directions (Figure 17 ).
![]()
Figure 14. Due to the physiological changes (first of all due to the blood-stream variation), the linear dependence breaks. (a) is the simplest saturation; when the SAR is moderate, the temperature rise is relatively slow (this is the case in most regional treatments); (b) the SAR is high enough for sudden temperature changes, while the physiological thermal feedback reacts only later, and regulates the saturation value (this is the case in high energy local treatments); (c) the SAR is extremely large, feedback is not able to moderate the temperature, it toxically burns (this is the case in most ablation treatments).
Selection of the energy absorption defines the efficacy of the actual treatment. It could be shown microscopically that the extracellular matrix and the cellular membrane absorb the main energy at a definite interval of radio-frequency (RF) [70] . According to calculations [71] - [73] , a relatively small amount of energy could heat up average-sized tumours to the appropriate temperature if it targets the tumour accurately enough [25] . The selection could be in the nano-range [74] - [87] . The main selective factors use the complex heterogeneity of the living
![]()
Figure 15. Effect of the vasodilation/vasocontraction threshold. (a) Perfusion rate of blood vs. temperature (the threshold cuts at 42˚C); (b) Temperature dependence of SAR (The specific heat of blood was given 3500 [Ws/K/m3]).
![]()
Figure 16. The energy consumption of the cellular distortions and chemical changes decrease the SAR converted to heating only (a); comparison of the pure heating and mixed effects (b).
![]()
Figure 17. Typical hysteresis phenomena (c) by heating up (a) and cooling down (b).
system, as well as the high metabolic activity of tumours and the absent strong cellular networking.
The selection causes a gain in SAR, which is very different depending on the heterogeneity of the tissue. The simplest (and relatively small) selection factor is the conductivity. The SAR gain vs. the ratio of conductivity shows about a 12% gain (Figure 18 ).
The SAR gain is a factor of the possible focusing energy; however, the BP changes the situation drastically, even at homogeneous SAR. As shown above, there is a threshold of temperature in tumours when the vasodilatation turns, and vasocontraction happens. This threshold makes well emphasised changes [58] . The results show different slopes for SAR to maintain the given temperature constant in the tumour-tissue. At high temperatures (over the threshold), the BP selects the tumour (Figure 19 ).
4. Discussion
One of the most polarising challenges among specialists is the question: does hyperthermia by electromagnetic heating have any non-temperature derived (many times it mentioned as “non-thermal”) effects or it is purely temperature dependent (“thermal”)? First, we have to clarify what we mean by the word “thermal”. Does it mean that it is heat connected or is it a temperature connected phenomenon? This question is not evident in discussions of the effect of SAR on temperature.
According to every day-use, the observed thermal effects are temperature-dependent. Naturally, the non-tem- perature-dependent but heat-connected effects are also thermal. This is very similar to the considerations made with steam-engines: the water is heated up until the boiling point of water is reached and an appropriate amount of steam is developed. After this point, no temperature change occurs in the system; all of the heat energy from the fuel is used for the desired mechanical movements and to replace the waste energy in the system. This effect from the point when the dynamic equilibrium (stationary process) has been set is absolute, not temperature- dependent (non-thermal); it is heat-dependent (we have to pump heat-energy in to keep the process going, without any observable change in temperature). We keep this unfortunately very flexible definition of the thermal or non-thermal conditions to be consistent with the widely accepted terminology of hyperthermia.
What does the heat pumped into the system do when the temperature does not change? It simply:
・ rearranges the structures (order → disorder transition),
・ triggers chemical reactions (using activation energy from heat),
・ breaks structural bonds (using energy impact to destroy the bond),
・ supplies resonance phenomena (using stochastic or quantum effects).
Hyperthermia uses the absorbed energy for all of the possible effects listed above. The energy-consumption for these processes could be called “non-thermal”, but this is actually incorrect. These need energy pumped in from outside sources, which is used by the actual process. The energy could be electromagnetic, which is not heat at the moment of chemical or quantum interactions. However, due to the thermodynamic entropy law, all interactions have dissipation. The dissipative part of the energy definitely heats the system. Typical processes are in metabolism, when the energy production is purely chemical, but the energy dissipation produces heat, which maintains the temperature of the tissue.
There is a modern MRI practice of temperature measurement using a calibrating phantom which typically ignores the real work (exergy) of the energy. It concentrates on the anergy only, which develops the temperature
![]()
Figure 18. Gain of SAR due to the heterogeneity of conductivity. (a) SAR increase by relative conductivity; (b) Temperature dependence of gain of SAR.
![]()
Figure 19. (a) Change of BP vs. depth; (b) Temperature development in the centre of the tumour; (c) Change of dissipation in depth at different time points; (d) Change of temperature in depth at different time points.
by complete energy dissipation, regarding pure water as the calibration phantom [78] [79] . In this case, the measured temperature in the tumour corresponds to the pure water, which means that no energy was used for cellular distortion. We know well that cellular distortion modifies the MRI time-shifts [80] - [82] , so the water- phantom is a misuse of this concept. It should be noted that the distortion-free increase in temperature approaches other goals: making optimal conditions and gaining efficacy enhancement for other complete therapies.
Living organisms show definite heterogeneity; consequently, the homogeneous SAR is illusory. The concept of isothermal, homogeneous heating of the local tumour does not work. The situation does not reach equilibrium, and due to the feedback regulations, even the stationary situation is rare. We have to accept the real situation: the technically difficult focus of SAR does not mean a focus of temperature, which depends on many processes, and naturally changes by time elapsed, spreading over the neighbours; also, a longer time increases the whole body temperature. The consequence of the selective and direct chemical process anyway challenges the idea of equal heating; local hyperthermia has non-equilibrium energy-distribution in all cases.
Most electromagnetic heating cause field and temperature gradients in microscopic scales, together with gradients of other thermodynamic intensives (e.g. pressure, chemical potential, electric field, surface tension, etc.) The constructed gradients are the driving forces for internal flows and changes. When the energy intake (the SAR value) is too high, then the microscopic effects are neglected, and most of the time, vanish, because the high temperature intending to equalise the absorption goal is isothermal stationary mass-heating.
These are microscopically definitely thermal processes, which are absolutely governed by the temperature gradients in the usual way of non-equilibrium thermodynamics. At the microscopic level, we cannot speak of any non-temperature-dependent (NTD) effects; also, the “non-thermal” and “athermal” categories are also incorrect characterisations of this situation. However, macroscopically, the temperature change is not necessarily expressed; even the most drastic microscopic temperature gradients could be hidden in a macroscopic average.
We are definitely facing two different tasks by the application of hyperthermia:
1) Set hyperthermia conditions which destroy malignant cells, directly affecting the oncologic paradigm. The definitive energy-absorption has to cover the biochemical effects and reactions, and only the part which is unused increases the temperature of the whole volume that is treated. Pumping energy into the target to make sure that it has an effect there results in such inequalities (gradients), which would be the driving force of the work. For this, we need working energy in the target, not an equal temperature which prefers equilibrium, and excludes gradients (The picture is naturally different when we make temperature gradients at the microscopic level, but it will not necessarily increase the temperature, or at least will increase it much less than in the gradient-less situation).
2) The point is that temperature is an important initialising parameter used to push the system from the actual dynamic equilibrium to other completing therapies. If the task which we expect to perform is not a direct distortion of the malignant cells, but providing better (optimal) conditions for other, more drastic methods to be achieved, then the temperature would be the active parameter. Higher temperatures could enable more active drug-reactions in chemotherapy or produce better conditions for radiotherapy by promoting blood perfusion (oxygenation). However, in this case, the selection at the cellular level is important to selectively promote the actions of the completed treatment.
In both cases, the selectivity and complex interactions, which modify the energy-absorption, have to be considered (There are conductive and convective heat-transfers as well as active biological heat-production which modifies the temperature of the target).
Nowadays, clinical practice uses the categories of patients: “heatable” or “non-heatable”, for selection (inclusion criteria) into hyperthermia clinical trials [83] . The selection is based on the possibility of the temperature increase in the actual location by local/regional treatment failing to reach the desired temperature in the target. The “non-heatable” cases could have the same SAR as the “heatable” ones, but their intensive homeostatic control blocks the marked temperature increase. This selection puts the patients into incorrect categories when measured by temperature if hyperthermia is used as a distortion tool. The distortion is an energy-dependent mechanism, and the missing measurable temperature increase does not necessarily mean that the absorbed energy is not used for the distortion. If the “heat-ability” categorisation is made to select patients for optimal completion of other therapies, it could be considered the correct selection. For this distinction, clear terminology is mandatory.
Cell killing requires energy. In this process, the overall energy of the system decreases from a well-ordered state to a disordered one. To break chemical bonds and make structural rearrangements, energy is invested. In this way, the absorbed energy (at least a part of it) will not increase the temperature; the breaking of the chemical bond comes directly from the energy. Energy must be pumped into the system for the transition energy, for example from the ordered state to the disordered one.
The non-temperature-dependent effects are usually referred to in interactions with electromagnetic fields. This distinction often depends on the applied power, which does not have enough energy to increase the temperature, but has an effect of the applied radiation (field) that is measurable [84] . The distinction was also theoretically described [85] by a shift in concentration on both sides of the membrane, and tries to determine the threshold below the electromagnetic energy absorption which is regarded as non-thermal. Others are formulating this situation as a “subtle” thermal effect [86] [87] . From the thermodynamic point of view, all energy-kind is a term in the energy-balance (see Equation (1)), irrespective of whether it changes the temperature or not. The only point is the addition to the internal energy of the system. The temperature change in the internal energy means unidirectional “smeared” energy is incorporated by the system, with distribution of the energy to all parts and particles involved in the system. However, the directional energy intake is selective; it acts only for particles, which are involved in this particular interaction. (E.g. electric field acts on the charges, the quantum/chemical effects act on special selection rules, etc.), but only a set of the parts and not all of the substances of the system are involved. In this case, the energy does the job by the purpose-made interaction, and it could be that the excess energy is distributed to other parts of the whole set of the parts of the system. When the energy transfer is correctly targeting the goal, then all of the pumped-in energy is devoted to achieving the desired task and to not “waste” the energy by distributing it to all of the involved parts. Changing the specially targeted chemical bonds could be done by that particular chemical effect which makes the energy-intake only to that reaction, but also could be done by increasing the energy of the whole system and its parts, reaching the desired energy intake in the reaction that it was originally intended to change.
The temperature-dependent effects are definitely macro-scale processes, but these are irrelevant for the microscopic changes; however, the electromagnetic interactions are micro-effects. Again we have to emphasise the following: the NTD effects certainly could be part of the thermodynamics (of course the non-equilibrium one) but this does not mean that these are non-thermal or “athermal”; they only have no macroscopically measurable temperature changes.
Logically, we expect the changes in terms of the internal energy, regarding the fact that the biological objects are more chemical than thermodynamic systems. The chemical energy-exchange can be described in the frame of the non-equilibrium thermodynamics, considering non-linear (phase transition like) effects and definite chemical reactions. It is known that living matter needs nutrition from the environment, as it would not be sufficient to simply have equivalent energy from heat-exchange. It was clearly formulated by Adey in 1993 [88] : “There is increasing evidence that these events relate to quantum states and resonant responses in biomolecular systems, and not to equilibrium thermodynamics associated with thermal energy exchanges and tissue heating”.
Many observations were made on various electromagnetic energy-absorption without mentioning temperature changes. The electric field promotes cellular fusion at low [89] and high [90] frequencies; a field-strength-de- pendent haemolytic effect was observed by RF exposure [91] , activation of ion-channels at the cellular membrane [92] , membrane mediated Ca2+ signalling affects the immune system, [93] , and transmembrane Ca2+ was induced by alternating current (low frequency electromagnetic fields [LFEMF]) [94] . Also, the biological effects of LFEMF have raised significant interest and debate in the past. Numerous reviews [95] [96] and articles report the responses of biological matter to LFEMF [97] - [105] .
5. Conclusion
The interconnection of SAR and temperature in biological systems is a complex phenomenon, determined by the thermal homeostasis of the biological system and the heterogeneity of the target. The linear dependence of SAR and temperature may happen only at large SAR values, where inhomogeneity and homeostatic control could be neglected.