Gas Production from Offshore Methane Hydrate Layer and Seabed Subsidence by Depressurization Method ()
Received 11 January 2016; accepted 20 June 2016; published 23 June 2016

1. Introduction
Methane hydrates (MH) has been expected to be the next-generation natural gas resources. Most of MH is reserved in marine sediments or permafrost in the offshore area of 900 km2 at Eastern Nankai Trough located at pacific coast of Honshu island in Japan. According to Fuji et al. (2008) [1] , MH potential in place was evaluated roughly to be equal to Japanese domestic gas consumptions over 10 years.
As gas production methods from MH reservoirs, depressurization, thermal stimulation, inhibitor injection, N2, CO2 or their mixing gases injection have been proposed and studied to enhance in-situ MH dissociation in considering MH equilibrium condition presented by Pooladi-Darvish (2004) [2] . If the conventional offshore drilling and gas production methods are applied, the depressurization method has been evaluated as an economical method by Kurihara et al. (2009) [3] , Yang et al. (2016) [4] and other researchers. Therefore, the first offshore MH production test was done by applying depressurization method at the Eastern Nankai Trough on March 2013, and approximately 120,000 m3 of natural gas was produced for six days. Moridis et al. (2010) [5] presented excellent reviews on the commercial gas production from MH reservoirs. On the other hand, the integrated thermal production system by injecting hot water injection using horizontal wells has been proposed by Sasaki et al. [6] [7] .
For the case of depressurization method, bottom-hole pressure (BHP) at a producer is reduced by the lowering hydraulic head by pumping up water in the producer, and MH dissociation process in the reservoir begins after pressure propagation from the producer. Depressurization must be kept to maintain gas production rate or MH dissociation rate. The MH dissociation-rate is proportional to heat transfer rate to the MH from outside sands and water with available sensible heat which depends on the difference between present temperature and MH equilibrium temperature corresponding to the MH pressure after depressurization.
However, depressurization and the decrease of solid saturation by the MH dissociation induce consolidation of MH reservoir and nearby sediments. The seabed subsidence is summation of deformation propagated from the three dimensional consolidation in sediment layers lower than the seabed. The depressurization causes increasing effective stress and reducing fluids permeability that makes low pressure propagation speed and low gas mobility in the MH reservoir. As a result, MH dissociation and gas production are suppressed by those processes connecting each other.
The reservoir consolidation and seabed subsidence are important issues to keep gas production rate from MH reservoir and control stabilities of seabed, sediment layers and producer. In this research, the numerical model considering MH dissociation and consolidation has been presented by history matching with the laboratory experiments carried by [3] using with the thermal simulator CMG STARSTM. The model includes reservoir rock mechanical stiffness function of MH saturation and consolidation. The applicability of present numerical model was confirmed by comparing with other numerical simulation results. Furthermore, numerical simulations for typical MH reservoirs with field-scale were carried out to predict gas production and consolidation behavior. From the point of view of seabed subsidence and heat supply, the method using hot-water injection and relatively low depressurization has been studied by comparing the depressurization method with high depressurization.
2. Numerical Simulation Model on MH Dissociation and Consolidation
Once depressurization method is applied for a reservoir, pore pressure is decreased, and effective stress (= confining stress-pore pressure) is increased simultaneously. Further MH reservoir at Eastern Nankai trough is an unconsolidated sand sediment-layer that makes easy to induce the consolidation with increasing effective stress. The coordinate system of numerical simulation model considering consolidation of MH reservoir and seabed subsidence is shown in Figure 1.
2.1. MH Dissociation
The reservoir simulator CMG STARSTM was used for numerical simulations on gas production and consolidation based on MH dissociation and elasticity function of MH saturation. In the simulations, MH was defined as solid phase that saturation in MH reservoir porosity reduces absolute permeability with power function [3] . According to Singh et al. (2008) [8] , the MH dissociation rate was calculated by the MH formation-decomposi- tion equilibrium curve [pressure; P(MPa), temperature: T(˚C)] of for phase transition from solid to fluid phases in sea water (3% NaCl) was given by the following equation;
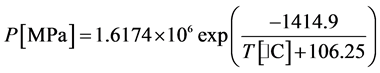 (1)
(1)
![]()
Figure 1. Schematic figure showing gas production from MH layer and consolidation by depressurizing reservoir.
Figure 2 shows the MH equilibrium curve for salt water with comparison to the experimental results presented by Sloan (1998) [9] . The equilibrium temperature of the water is almost 1.0˚C is lower than that of sea water. Thus, the equilibrium equation line for water, which is shown in Figure 2, is derived by setting 105.25 instead of the value of 106.25 in Equation (1). Other thermal quantity and MH decomposition heat were given based on compositions (solid, gas and water) in MH reservoir blocks.
2.2. MH Reservoir Porosity and Absolute Permeability
The increase of MH saturation (solid phase) results in sharply decrease of relative permeability due to decrease of apparent porosity in the MH reservoir. Conversely, apparent porosity and permeability increase rapidly by MH dissociation. In addition, porosity depended on congenital compressibility of MH reservoir is decreased by increase of effective stress with depressurization. In this numerical simulation, effective porosity, which depends on MH saturation, compressibility and depressurization, is defined by following Equations (2) and (3).
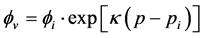 (2)
(2)
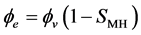 (3)
(3)
where
ϕv: Porosity [-]
ϕi: Initial porosity [-]
κ: Compressibility [MPa−1]
p: Reservoir pressure [MPa]
pi: Initial reservoir pressure [MPa]
φe: Effective porosity [-]
SMH: MH saturation [-]
The initial permeability of MH reservoir is remarkably low at the initial condition which has high MH saturation over 50%, however the apparent permeability of MH reservoir is improved rapidly with MH dissociation [3] . On the other hand, porosity of MH reservoir is decreased by the consolidation depended on depressurization, therefore absolute permeability of MH reservoir is decreased simultaneously. In this research, following Equation (4) based on Kozeny-Carman equation which represents the relationship of permeability-porosity.
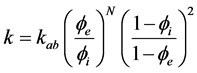 (4)
(4)
where
k: Apparent permeability [m2]
kab: Absolute permeability [m2]
![]()
Figure 2. MH dissociation equilibrium curve with comparison to the experimental results in water presented by Sloan (1998) [9] .
N: Permeability reduction index (=6) [-]
2.3. Models of Relative Permeability and Consolidation Based on Sakamoto et al.’s Experimental Results
In present research, the experimental results by [10] were referred for constructing MH dissociation and consolidation models to check a model of permeability-porosity in MH reservoir during depressurization process. Their laboratory experiments were done to study MH dissociation, consolidation, temperature and permeability characteristic in a sand-pack including synthetic MH (hereinafter call as “MH core”) as shown in Table 1. The temperature distribution was measured by thermocouples set with 5 cm intervals in radial and axial directions in the MH core.
The relative permeabilities were presented by Sakamoto et al. (2010) [11] for the MH core by following Equations (5) and (6).
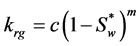 (5)
(5)
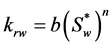 (6)
(6)
where
krg: Gas relative permeability [-]
krw: Water relative permeability [-]
c: End point for gas relative permeability [-]
b: End point for water relative permeability [-]
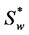 : Normalized water saturation [-]
: Normalized water saturation [-]
m: Index of gas relative permeability krg [-]
n: Index of water relative permeability krw [-]
The numerical block models in cylindrical coordinate were made for the laboratory experiments. Outer radius and height of the stainless cell are 89.4 mm and 144 mm (see Figure 3). The total number of cylindrical-grid blocks was 1612 with 31 in z-direction and 52 in r direction. The stainless section was set as a constant temperature and closing state. The initial conditions of the numerical model are listed in Table 1. The equilibrium curve for MH formation and dissociation was given by the same equation presented by Sasaki et al. (2014) [6] . The history matching simulations on the experimental results were carried out by using the STARS.
Equations (4) and (5) presented by [11] were used for the relative permeabilities in the numerical history matching. In the case of high water saturation in the MH core, water is produced selectively and gas is remained
![]()
Table 1. Initial condition of synthetic MH core made of No. 7 quartz sand [10] .
![]()
Figure 3. Experimental set up of methane hydrate sand-pack in pressure cell [10] and numerical block model used for simulations by CMG STARSTM (total number of grid-brocks = 1612).
in pores by capillary pressure. The values of m and n were set as 10 and 3 in the Equations (5) and (6) respectively in order to represent that water has higher mobility than gas in the region of high water saturation.
2.4. Reservoir Elastic Model Based on the Laboratory Measurements
As shown in Figure 4, Masui et al. (2005) [12] and Miyazaki et al. (2005) [13] have presented the relationship between MH saturation and elastic modulus, E by the tri-axial compression test using the MH cores. It means that E value is increased linearly with increasing MH saturation in MH cores. In this research, it was assumed that elastic modulus and compressibility can be given by the following equation.
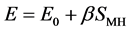 ;
;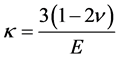 (7)
(7)
where
κ: Compressibility [MPa−1]
ν: Poisson’s ratio [-]
E: Elastic modulus of MH reservoir (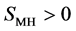 ) [MPa]
) [MPa]
E0: Elastic modulus of sands (Rock matrix) (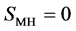 ) [MPa]
) [MPa]
SMH: MH saturation [-]
β: Increase rate of elastic modulus vs. ![]() [MPa]
[MPa]
![]()
Figure 4. Relationship of elastic modules vs. MH saturation based on the measurement results by Masui et al. (2005) [12] .
2.5. Numerical Modeling of Seabed Subsidence
Seabed subsidence is induced by decrease of porosity of sediment layers and the MH reservoir consolidation. In this research, the amount of seabed subsidence was evaluated as summation of vertical compaction in a grid at each distance from the seabed to MH reservoir given by
![]() ;
;![]() (8)
(8)
where
Δh: Displacement of seabed [m]
z: distance from seabed [m]
α: Subsidence ratio [-]
ζ: Distance index of subsidence [1/m]
The subsidence ratio (α), that has the value from 0 to 1, is contributing ratio of each grid’s displacement at z on the seabed subsidence at z = 0 based on Aoki et al. (1991) [14] and Nishida et al. (1981) [15] . In the case of the laboratory experiments on sand pack consolidation discussed in the next section α was set as α = 1.0, because z is very short comparing to a field.
2.6. Numerical History Matching to the Laboratory Experiments
Authors have done the comparisons of cumulative methane gas and water productions between the laboratory experiments and present numerical simulation (see Figure 5). In the both results, water is produced rapidly in early stage after depressurizing, and gas is produced after water. However, it is clear that there are differences between numerical and experimental results. The reason of the difference was made from the models on gas and water relative permeabilities presented by Equations (5) and (6). Sakamoto et al. [11] also carried out the numerical history matching for the laboratory experiment, and they showed better matching results than present results. However, we have succeeded to get better matching results by considering effects of consolidation in the MH core as described.
Figure 6(a) shows the comparison of displacements at the point of 4.75 cm from center in the MH core. The numerical result on the displacement at the end of experiments showed almost same value with the experiment, however, displacement shows different behavior at the early stage of depressurization. It was assumed that MH has an effect to make larger elastic modulus (Young’s modulus) with cohesive strength by connecting unconsolidated sand grains.
The displacement behavior was recalculated by using modified compressibility considering cohesive strength of MH with varying initial elastic modulus of rock matrix E0 = 100 to 200 MPa, Poisson’s ratio ν = 0.2 to 0.6
![]()
Figure 5. Comparisons of cumulative methane gas and water productions between the laboratory experiments and present numerical simulation.
and increase rate of elastic modulus β = 600 to 1000 MPa based on experimental results presented by Masui et al. (2005) [12] and Miyazaki et al. (2005) [13] . When the values, that are E0 = 200 MPa, ν = 0.217 and β = 700 MPa, were used, the numerical simulation result showed the best matching with the experiments by [13] . Figure 6(a) shows the result of history matching of displacement behavior using modified elastic modulus and compressibility that is the function of MH defined by Equation (7). As shown in Figure 6(a), the final cumulative displacement shows same value when MH dissociation finished. However, it is clear that matching degree of the numerical simulation with Equation (7), E = E0 + βSMH, is better than that with E = E0 = constant.
The comparison of temperature distributions between the laboratory experiment and present numerical simulation is shown in Figure 6(b). Temperature in the MH core was decreased from 10.7˚C to 2˚C by endothermic reaction during MH dissociation. The temperature of 2˚C is equal to equilibrium temperature for pressure of 3.3 MPa. After finishing MH dissociation, temperature of the MH core was increased from 2˚C to 10.7˚C by heat supply from the stainless cell. The numerical results also showed almost the same temperature distribution measured by the experiments.
As shown in Figure 7, the cumulative gas production for the initial MH core temperature of 2˚C was approximately 18% of that of 10.7˚C in the present numerical simulation. In the case of 2˚C, MH dissociation was suppressed due to small heat supply by small temperature difference between initial core temperature and MH equilibrium temperature after depressurization.
It was confirmed that present numerical simulation model can be used for simulating MH dissociation process and consolidation behavior in laboratory scale based on the history matching results presented in [10] .
3. Numerical Simulation Results and Discussions
3.1. Validity of MH Dissociation Model in Field Scale
Comparative studies on numerical MH model were done by [3] to investigate the validity of present numerical simulation model for gas production from field scale of MH sediment layers by depressurization method. Numerical simulations were carried out by using MH21-HYDRES (Kurihara et al., 2011) [16] developed by MH21 reserch consortium.
In the comparative studies, typical properties of MH reservoir at Eastern Nankai Trough given in Table 2 were used, since these data were presented by [3] for their numerical simulations on gas production by depressurization method. Figure 8 shows cylindrical coordinate (r, z) of MH reservoir model in field scale. The reservoir consists of 44 units of mud, silt and sand layers, that structure assumes a turbidite sediment layer. The
![]() (a)
(a)![]() (b)
(b)
Figure 6. Comparison of (a) longitudinal displacements by sand-pack experiment and (b) temperature longitudinal-distributions [10] and present numerical simulations with non-consolidation model and consolidation model considering elastic modulus function of MH saturation.
pressure difference 10.2 MPa between initial reservoir pressure 13.2 MPa and bottom-hole pressure 3.0 MPa was applied for depressurization in the MH reservoir.
3.2. Influence of Sand Consolidation on Gas Production
The numerical simulations in considering field-scale sand consolidation were carried out by the considering model presented in the previous section based on matching with the laboratory experiments. Hereinafter simulations without consolidation or porosity change by setting E0 = ∞ are called as “base case” that was compared with ones considering consolidation in MH reservoir where E0 = 200, 140 and 80 MPa were given for sand layer, silt layer and mud layer, respectively, while ν = 0.217 was given for three layers that were presented by Yoneda (2013) [17] .
As shown in Figure 9, gas production behaviors by present and Kurihara et al.’s numerical simulation results [3] [17] are compared for of the base case without applying consolidation effects on them. Both numerical simulations show favorable matching except little differences in, peak production rate, declining trend after the peak rate and cumulative gas production that are 3.6 × 107 and 3.8 × 107 m3 respectively. It is concluded that
![]()
Figure 7. Numerical simulation results on cumulative gas production.
![]()
Figure 8. Definitions of cylindrical coordinates (z, r) and a typical MH reservoir at Eastern Nankai Trough [3] .
![]()
Table 2. Physical properties of a typical MH reservoir at eastern Nankai Trough [3] .
present model has almost applicability for gas production from MH reservoirs in field scale, because little differences in modelling of relative permeability, heat capacities and pressure-temperature equilibrium between two models made effects on pressure propagation, MH dissociation and gas production.
Figure 9 also shows the effect of the elastic modulus, E0 in the consolidation model on gas production behaviors. It was confirmed that time showing the peak rate was approximately 530 days that is longer than 290 days of the base case, while the gas peak rate decreased to 45% of the base case. The decrease of absolute permeability by sand consolidation makes delay of pressure propagation and gas peak rate, however, the cumulative gas productions at 1825 days were approximately same value of 32 × 106 m3. After 1600 days, bottom-hole pressure propagated to whole reservoir region, therefore gas production rate or MH dissociation rate depends on reservoir permeability and heat supply to MH reservoir from upper and lower sediment layers. The peak times of gas production rate delayed with decreasing value of E0. The time showing the peak production rate was around 400 to 930 days for E0 = 100 to ∞ MPa. However, the differences of cumulative gas productions after 2200 days are much smaller than that of early stage after start of depressurization. Based on calculation results of absolute permeability and pressure distributions in radial direction, it was confirmed that pressure propagation has strong relation with MH dissociation process and gas production behavior.
3.3. Prediction of Seabed Subsidence by Depressurization
Numerical simulation of seabed subsidence was done for the MH reservoirs with two models of elastic modulus expressed by E = E0 and E = E0 + βSMH. To decide the subsidence ratio α, field measurement data are required. In this research, the value of water-dissolved gas field, ζ = 0.0012 which was reported by [14] [15] was used for present numerical simulations.
Seabed subsidence behaviors were simulated for two models of elastic modulus to predict the largest subsidence and the largest gradient of subsidence. Figure 10 shows predictions of seabed subsidence for different
![]()
Figure 9. Comparison of gas production behaviors between present and Kurihara’s numerical simulation results without consolidation models, and predictions of gas production behavior for different values of the elastic modulus, E0 (Initial reservoir pressure = 13.2 MPa, BHP = 3 MPa).
![]()
Figure 10. Predictions of seabed subsidence at 50 days for different elastic modulus of rock matrix, E0 (Initial MH reservoir pressure = 13.2 MPa, BHP = 3.0 MPa).
values of E0 at 50 days from start of depressurization. In both of the models, the maximum amount of the subsidence becomes larger with decreasing E0. For the model of E = E0, values of the largest subsidence, Δhmax = 1.4, 1.6 and 2.0 m for E0 = 100, 200 and 400 MPa, respectively, and radius boundaries, rB showing the value of subsidence Δh = 0.1 m are calculated as rB = 31.8, 40.0 and 47.0 m for E0 = 100, 200 and 400 MPa, respectively, while for the model of E = E0 + βSMH, Δhmax = 0.50, 1.0 and 1.85 m and rB = 30.2, 34.8 and 36.4 m for E0 = 100, 200 and 400 MPa, respectively. The differences of two models are caused by existence of residual MH biding sand grains. It is estimated that the residual MH increases appearance elastic modulus of MH reservoir, then the seabed subsidence is controlled.
4. Conclusions
In this study, the consolidation-permeability compound model has been applied for numerical simulations on gas production from offshore methane hydrates (MH) reservoir. The model has been constructed by numerical history matching with experimental results on MH dissociation and consolidation by depressurization using the synthetic sand core presented by [10] . The numerical simulations on gas production from a typical MH reservoir model at Eastern Nankai Trough, Japan by applying depressurization method were also carried out, and validity of present models on MH dissociation and consolidation was evaluated by comparisons with the results presented. Finally, seabed subsidence during gas production was numerically predicted for MH reservoirs that elastic modulus (at MH saturation = 0) varies from 400 to 100 MPa. The maximum seabed subsidence has been expected to be roughly 0.5 to 2 m after 50 days of gas production from MH reservoirs.
In our next study, the methodology presented in this paper will apply to simulate seabed subsidence during gas production by a thermal production method with hot water injection using horizontal wells proposed by authors [12] [13] . Its seabed subsidence is expected to be less than that of the depressurization method.
Unit Conversion
md = 9.8E−16 m2
![]()
Submit your manuscript at: http://papersubmission.scirp.org/