Heat Transfer Efficiency of Turbulent Film Boiling on a Horizontal Elliptical Tube with External Flowing Liquid ()
Received 17 March 2016; accepted 8 May 2016; published 11 May 2016

1. Introduction
The pioneering investigator, Bromley [1] , conducted the research of film boiling on a horizontal tube. After Bromley’s research, many related researches had been reported. In 1966, Nishikawa and Ito [2] analyzed two- phase boundary-layer treatment of free-convection film boiling. The theoretical study investigated on film boiling from an isothermal vertical plate and a horizontal cylinder without considering radiative effects. Jordan [3] investigated the laminar film boiling and transition boiling, and the also discussed the separated region. Sakurai et al. [4] presented the pool film boiling on a horizontal cylinder with theoretical solutions. The analytical heat transfer model was based on laminar boundary theory including radiation effects. Besides, Huang et al. [5] conducted the research on the forced convection film boiling. They investigated the flow film boiling across a horizontal cylinder with uniform heat flux. The numerical results agreed with experimental data where the wall temperature did not vary a lot around the heater at high heat fluxes.
Laminar film boiling had been widely discussed in published literature, and so has turbulent film boiling. For example, Sarma et al. [6] presented turbulent film boiling with consideration to thermal radiation for the vertical surface. In the research, the assumption of equal shear condition both at the wall and the vapor-liquid interface was reasonable. Later, Sarma et al. [7] presented some theoretical results about the turbulent film boiling on a horizontal isothermal circular cylinder. The analysis compared the theoretical results with previous experimental results, and found that their results were in a good agreement with the experimental data. Hu [8] presented the surface tension effects in boiling heat transfer of cryogenic LN2 on an ellipsoid. However, the study just researched into a simple theoretical model for turbulent film boiling heat transfer on an ellipsoid under a quiescent liquid. Furthermore, Hu [9] investigated the influences of interfacial shear in turbulent film boiling on a horizontal tube with external flowing liquid.
Even though there were many researches about laminar film boiling and turbulent film boiling, there was little publication about the turbulent film boiling on a horizontal elliptical tube which his high velocity liquid was flowing outside. Predicting interfacial shear in a turbulent film boiling system under high velocity liquid was not easy. However, the present paper successfully predicted the vapor-liquid interfacial shear by using Colburn analogy. The present study applied the interfacial shear into the forced balance equation, and then combined the forced balance equation with the energy equation and thermal energy balance equation. At last, both the film thickness and Nusselt number were obtained. Then, the present analysis also included eddy diffusivity, radiation effects and temperature ratio. Finally, a comparison between the results of the present study and those reported in previous experimental studies was provided. It was found that a good agreement exists between the two sets of results.
2. Formulations
Consider a horizontal elliptical tube immersed in an up flowing LN2 of the high velocity  at saturated temperature Ts. The wall temperature
at saturated temperature Ts. The wall temperature  is assumed high enough to induce turbulent film boiling on the surface of the elliptical tube, and then a continuous film of vapor runs upward over the surface. The physical model and the coordinate system adopted in the present study are shown in Figure 1, where the coordinates is use two-dimen- sional orthogonal curvilinear coordinate system.
is assumed high enough to induce turbulent film boiling on the surface of the elliptical tube, and then a continuous film of vapor runs upward over the surface. The physical model and the coordinate system adopted in the present study are shown in Figure 1, where the coordinates is use two-dimen- sional orthogonal curvilinear coordinate system.
![]()
Figure 1. Physical model and coordinate system.
For thin film flow of turbulent film boiling under the forced convection, the viscosity component and the buoyancy effect are assumed more significant than the inertia force. Then the force balance equation for the vapor film can be expressed as:
 (1)
(1)
It is assumed the thickness of vapor film is much thinner than the diameter of the tube ( ). And it’s further assumed the turbulent conduction term across the vapor layer is more significant than the convective term, and hence the convective term can be neglected. The energy equation can be expressed as:
). And it’s further assumed the turbulent conduction term across the vapor layer is more significant than the convective term, and hence the convective term can be neglected. The energy equation can be expressed as:
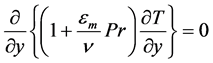 (2)
(2)
The boundary conditions of energy equation under isothermal condition are as follows:
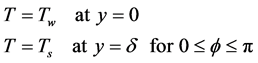 (3)
(3)
For a pure substance, the thermal energy balance equation of the vapor film can be expressed as:
 (4)
(4)
The differential arc length for ellipse can be expressed with the following equation:
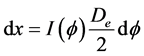 (5)
(5)
where
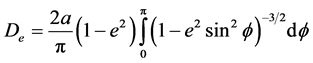 (6)
(6)
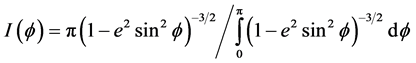 (7)
(7)
where  is an equivalent diameter based on the equal outside surface area, which is compared with circular tubes.
is an equivalent diameter based on the equal outside surface area, which is compared with circular tubes.
Substitute the  into thermal energy balance equation, and (Equation (4)) can be modified as follows:
into thermal energy balance equation, and (Equation (4)) can be modified as follows:
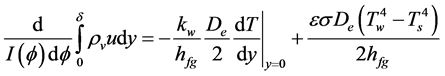 (8)
(8)
In the turbulent region the semi-empirical equation which describes heat transfer in the flow parallel to a moderately curved surface may also be used to describe the heat transfer in the flow parallel to an elliptical surface. Jakob [10] proposed that this situation may be described for any fluid by the following expression:
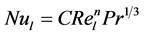 (9)
(9)
where C is a constant in flow configuration, C = 0.034.
According to Colburn analogy, the friction factor can be written as the following equation:
![]() (10)
(10)
The mean friction coefficient in the streamwise direction may then be calculated as:
![]() (11)
(11)
Furthermore, the local friction can be obtained as:
![]() (12)
(12)
The turbulent boundary layer exerts a friction force on the liquid-vapor boundary. The shear stress is estimated by considering the external flowing liquid across the surface of the tube when there is no vapor film on the surface. The local shear stress is defined as:
![]() (13)
(13)
According to potential flow theory, when the uniform liquid flow of velocity ![]() passing a tube, the liquid velocity at the edge of the boundary is as follows:
passing a tube, the liquid velocity at the edge of the boundary is as follows:
![]() (14)
(14)
Combining Equations (12)-(14), the local shear stress can be expressed as:
![]() (15)
(15)
Incorporating the interfacial vapor shear stress ![]() given by Equation (15) into the elemental forced balance equation enables Equation (1) to be rewritten in the following form:
given by Equation (15) into the elemental forced balance equation enables Equation (1) to be rewritten in the following form:
![]() (16)
(16)
The forced balance equation Equation (17) yields the following dimensionless equation:
![]() (17)
(17)
It’s further assuming the pressure across the boundary layer is constant and the density variation across the boundary layer is given by the following equation:
![]() (18)
(18)
The energy equation Equation (2) yields the following dimensionless energy equation:
![]() (19)
(19)
The dimensionless boundary conditions of Equation (19) are:
![]() (20)
(20)
where the absolute viscosity equation ![]() in dimensionless energy equation Equation (19) is expressed as the vapors of liquid nitrogen at the saturation temperature corresponding to a system pressure under 1 atm. i.e.
in dimensionless energy equation Equation (19) is expressed as the vapors of liquid nitrogen at the saturation temperature corresponding to a system pressure under 1 atm. i.e.
![]() (21)
(21)
Besides, the thermal energy balance equation Equation (8) can be rewritten in dimensionless form as follows:
![]() (22)
(22)
where the absolute conductivity equation ![]() in thermal energy balance equation Equation (22) is expressed as the vapors of liquid nitrogen the saturation temperature corresponding to a system pressure under 1 atm.:
in thermal energy balance equation Equation (22) is expressed as the vapors of liquid nitrogen the saturation temperature corresponding to a system pressure under 1 atm.:
![]() (23)
(23)
Furthermore, the dimensionless thermal energy balance equation Equation (22) requires the velocity profile ![]() in the vapor film. And
in the vapor film. And ![]() can be obtained by following equation:
can be obtained by following equation:
![]() (24)
(24)
The boundary condition is:
![]() (25)
(25)
The eddy diffusivity distribution presented by Kato et al. [11] is expressed as:
![]() (26)
(26)
The heat transfer of turbulent film boiling can be given by the following equation:
![]() (27)
(27)
Obviously, the local Nusselt number can be expressed as:
![]() (28)
(28)
The mean Nusselt number for the entire surface of the tube can be written as:
![]() (29)
(29)
3. Numerical Method
The dimensionless governing Equations (17), (22)-(26) and (28), (29) subject to the relevant boundary conditions given can be used to estimate![]() ,
, ![]() and Nu for the vapor film by means of the following procedures by using C++:
and Nu for the vapor film by means of the following procedures by using C++:
1) Suitable dimensionless parameters, such as e, ![]() , S, NR, Fr and
, S, NR, Fr and ![]() are specified.
are specified.
2) The boundary conditions of velocity and temperature are as follows:
![]() (30)
(30)
3) Since the ![]() at the bottom of the tube (
at the bottom of the tube (![]() , i = 0) is zero, the dimensionless film thickness δ+ is also zero (
, i = 0) is zero, the dimensionless film thickness δ+ is also zero (![]() ). At the next node, i.e. i = i + 1, the value of
). At the next node, i.e. i = i + 1, the value of ![]() is given by
is given by![]() , where
, where![]() .
.
4) Guess an initial value of![]() ; substitute Equations (21), (26) into Equation (19) and then get the value of
; substitute Equations (21), (26) into Equation (19) and then get the value of![]() .
.
5) Substitute![]() , Equations (23), (24) and (25) into Equation (22), and get the value of
, Equations (23), (24) and (25) into Equation (22), and get the value of![]() . After calculating, the values of
. After calculating, the values of ![]() can be gotten, and then substitute the values of
can be gotten, and then substitute the values of ![]() into Equation (17).
into Equation (17).
6) The criterion for the accuracy of ![]() is assessed by Equation (17), and it can be expressed as the following unequal equation:
is assessed by Equation (17), and it can be expressed as the following unequal equation:
![]()
If the calculation is a convergence, process the film thickness of next angular position. If the calculation is not a convergence, guess a new thickness and repeat processes (4)-(6).
7) The process above is repeated at the next node position, i.e.![]() , and then subsequently at all nodes within the range
, and then subsequently at all nodes within the range![]() .
.
8) The local Nusselt number and mean Nusselt number are then calculated.
4. Results and Discussion
Figure 2(a) plots the three-dimensional local velocity distributions in vapor film for Fr = 500. For each angular position ![]() on the entire tube surface, it is shown that with an increase in y+, u+ will increase to a maximum value, and then it will slightly decrease. The results also show that the dimensionless velocity increases with an increasing angular position on the elliptical surface. Figure 2(b) shows the two-dimensional equi-velocities in vapor film for Fr = 500. The dimensionless velocity at the wall of the elliptical tube is zero because of the no- slip condition and it will increase along the y-direction. This can be apprehended that the velocity will become larger due to the shear stress of vapor-liquid interface under the condition of flowing liquid.
on the entire tube surface, it is shown that with an increase in y+, u+ will increase to a maximum value, and then it will slightly decrease. The results also show that the dimensionless velocity increases with an increasing angular position on the elliptical surface. Figure 2(b) shows the two-dimensional equi-velocities in vapor film for Fr = 500. The dimensionless velocity at the wall of the elliptical tube is zero because of the no- slip condition and it will increase along the y-direction. This can be apprehended that the velocity will become larger due to the shear stress of vapor-liquid interface under the condition of flowing liquid.
Figure 3(a) shows the velocity distribution of the vapor film on the entire elliptical tube. Figure 3(b) presents the two-dimensional isothermal lines in the vapor film. For the boundary conditions prescribed in the proposed model, the dimensionless temperature on the tube surface and on the vapor-liquid interface are unity and zero respectively. Furthermore, the assumption of the stagnation flow is imposed at the bottom of the tube. As a result, the temperature variation along the vapor film thickness at ![]() is linear. In addition, the interfacial shear with high velocity liquid, and the effects of turbulence are considered in this work. As the angular position increases, the effects of eddy diffusivity get stronger and the non-linear temperature profile of the vapor film appears.
is linear. In addition, the interfacial shear with high velocity liquid, and the effects of turbulence are considered in this work. As the angular position increases, the effects of eddy diffusivity get stronger and the non-linear temperature profile of the vapor film appears.
Figure 4 displays the variation of the dimensionless vapor film thickness on the elliptical tube along![]() . Specifically, the film thickness increases continuously from a minimum value at the bottom of the tube
. Specifically, the film thickness increases continuously from a minimum value at the bottom of the tube ![]() and reaches its maximum value at the top of the tube
and reaches its maximum value at the top of the tube![]() . Besides, according to potential theory, the increase in the eccentricity value will lead to a decrease in the liquid velocity. And the decrease in the liquid velocity will lead to the decrease in heat transfer efficiency and evaporative rate. The former phenomenon will bring about the decrease in the film thickness. Besides, the figure also states the influence of Fr on the film thickness. The film thickness will increase when Fr values increase. An increase in Fr will bring out an increase in the interfacial shear stress and then leads to an increase in the evaporative rate. Consequently, the increase of evaporative rate may cause an increase of the vapor film thickness.
. Besides, according to potential theory, the increase in the eccentricity value will lead to a decrease in the liquid velocity. And the decrease in the liquid velocity will lead to the decrease in heat transfer efficiency and evaporative rate. The former phenomenon will bring about the decrease in the film thickness. Besides, the figure also states the influence of Fr on the film thickness. The film thickness will increase when Fr values increase. An increase in Fr will bring out an increase in the interfacial shear stress and then leads to an increase in the evaporative rate. Consequently, the increase of evaporative rate may cause an increase of the vapor film thickness.
Figure 5 presents the effects of eccentricity on mean Nusselt number under five different Froude numbers. According to the potential flow theory, the larger the eccentricity parameter is, the smaller the liquid velocity and interfacial shear are. Consequently, both the vapor velocity and the mean Nusselt number will decrease. Besides, under the condition of the forced convective film boiling, increasing Fr will result in an increase of the mean Nusselt numbers.
![]()
Figure 4. Dimensionless film thickness on tube surface.
![]()
Figure 5. Effects of the eccentricity parameter on mean Nusselt number.
Figure 6 presents the relationship between the mean Nusselt number and the Froude numbers for five values of Grashof number. The figure shows the results of the forced convection film boiling. A higher Froude number will bring an increase in the mean Nusselt. Besides, the Grashof number Gr is also one of the dominant factors, and therefore increasing the Grashof number will bring out an increase in the mean Nusselt.
To validate the present model, a comparison is made between this work and previous studies for different
cases. For this reason, a modified Rayleigh number is introduced as ![]() which can be further nondimensionalized in the form of
which can be further nondimensionalized in the form of![]() . Figure 7 depicts the ef-
. Figure 7 depicts the ef-
fects of Ra on the mean Nusselt numbers on an elliptical tube under e = 0 with special case of a tube subject to turbulent film boiling. It shows that the mean Nusselt number of the present study has a good agreement with previous experimental data [12] under the condition of quiescent liquid (i.e. Fr = 0 or![]() ). Besides, Num increases with Ra at fixed radiation parameter. The increase in the radiation parameter, conceivably, will bring out an increase in the mean Nusselt number at a given Ra.
). Besides, Num increases with Ra at fixed radiation parameter. The increase in the radiation parameter, conceivably, will bring out an increase in the mean Nusselt number at a given Ra.
Figure 8 shows the correlation of Rayleigh number and mean Nusselt number under five different Froude number. According the figure, the increase the Rayleigh number will bring out the increase the mean Nusselt number. Besides, the larger the Froude number will also increase the mean Nusselt number.
5. Conclusions
The following conclusions can be drawn from the results of the present theoretical study:
1) With the help of Colburn analogy, the present research successfully predicts the shear stress of the vapor- liquid interface in a film boiling system under liquid of high velocity on an elliptical tube.
2) The increase in the eccentricity parameter of the elliptical tube will lead to a decrease in the mean Nusselt number. Besides, turbulent film boiling under the external flowing liquid with high velocity, the increase in both the Froude number and Grashof number will bring out an increase in the mean Nusselt number.
![]()
Figure 6. Effects of the Froude number on mean Nusselt number.
![]()
Figure 7. Comparison of the present results with previous data.
![]()
Figure 8. Effects of the Ra on mean Nusselt number.
3) The present paper includes interfacial shear, radiation effects, temperature ratio, eddy diffusivity and thermal properties of temperature dependent. It can predict the forced convection turbulent film boiling more exactly. Besides, under the condition of free convection film boiling, it shows a good agreement between the present result and the previous experimental studies.
Acknowledgements
The authors gratefully acknowledge the support provided to this projects by the Ministry of Science and Technology of Taiwan under Contract Number MOST 104-2221-E-019-052.
Nomenclature
a, b semimajor, semiminior axis of ellipse
![]() specific heat capacity, (J/kg∙K)
specific heat capacity, (J/kg∙K)
De equivalent circular diameter of elliptical tube (m)
![]() shear Reynolds,
shear Reynolds, ![]()
![]() wall shear parameter,
wall shear parameter, ![]()
e eccentricity of ellipse, ![]()
Fr Froude number, ![]()
![]() modified Grashof number,
modified Grashof number, ![]()
g acceleration due to gravity (m/s2)
h heat transfer coefficient, W/(m2∙K)
hfg latent heat (J/kg)
k thermal conductivity (W/m∙K)
![]() dimensionless thermal conductivity,
dimensionless thermal conductivity, ![]()
![]()
![]()
![]() local Nusselt number,
local Nusselt number, ![]()
Num mean Nusselt number
NR radiation parameter, ![]()
Pr Prandtl number, ![]()
Ra modified Rayleigh number, ![]()
![]() Reynolds number of vapor,
Reynolds number of vapor, ![]()
![]()
![]()
S heat capacity parameter, ![]()
St Stanton number, ![]()
T temperature (K)
![]() temperature ratio,
temperature ratio, ![]()
T+ dimensionless temperature, ![]()
u vapor velocity in x-direction (m/s)
![]() shear velocity,
shear velocity, ![]()
![]() dimensionless velocity,
dimensionless velocity, ![]()
v velocity normal to the direction of flow (m/s)
![]() acceleration due to graviton force (m/s2)
acceleration due to graviton force (m/s2)
x peripheral coordinate (m)
y coordinate measured distance normal to tube surface (m)
y+ dimensionless distance, ![]()
Greek Symbols
![]() vapor film thickness (m)
vapor film thickness (m)
![]() dimensionless film thickness,
dimensionless film thickness, ![]()
![]() absolute viscosity (kg/m∙s)
absolute viscosity (kg/m∙s)
![]() dimensionless absolute viscosity,
dimensionless absolute viscosity, ![]()
![]() kinematic viscosity (m2/s)
kinematic viscosity (m2/s)
![]() density (kg/m3)
density (kg/m3)
![]() shear stress (N/m2)
shear stress (N/m2)
![]() angle measured from bottom of tube
angle measured from bottom of tube
![]() angle between the tangent to tube surface and the normal to direction of gravity
angle between the tangent to tube surface and the normal to direction of gravity
![]() interfacial shear parameter,
interfacial shear parameter, ![]()
![]() eddy diffusivity for momentum
eddy diffusivity for momentum
![]() emissivity
emissivity
![]() Stefan-boltzmann constant, W/m2∙K4
Stefan-boltzmann constant, W/m2∙K4
Subscripts
l liquid
s vapor at saturation temperature
v vapor
w tube wall
x x-direction
![]() vapor-liquid interface
vapor-liquid interface