Size and Weight Fraction of Solvent Crystals in Poly (Vinyl Alcohol) Gel Prepared from Dimethylsulfoxide/Water Solution ()
Received 25 February 2016; accepted 19 April 2016; published 22 April 2016

1. Introduction
Poly (vinyl alcohol) (PVA) is a representative water-soluble semicrystalline synthetic polymer that forms a physical hydrogel with crystallites as crosslinking points. The preparation of PVA hydrogel by a method involving alternate freezing and melting was first reported by Peppas et al. [1] This method offers several advantages compared with other methods such as chemical cross-linking [2] and radiation-induced cross-linking [3] because this sol-gel transformation is reversible against temperature and additional chemical reagents are not required for gelation. Willcox et al. investigated the molecular structure and morphology of PVA hydrogel prepared by alternate freezing and melting, and found that the hydrogel adopted a mesh structure crosslinked with crystallites [4] . They also estimated the degree of crystallinity, which was as low as a few percent, and the average separation among crystallites was about 30 nm. Ricciardi et al. quantitatively investigated the phase structure of PVA hydrogel, showing that there were three components: the PVA crystalline phase, a swollen amorphous phase including water, and pure water [5] - [8] . The degree of crystallinity was 2% - 6%, depending on the repeat time of the alternate freezing and melting process. With regard to molecular morphology, the PVA hydrogel is thought to adopt a porous structure filled with water.
Recently, we used thermal analysis to study the crystal size of ice frozen in a PVA hydrogel [9] [10] . The depression of the melting temperature of ice in the gel was interpreted as a function of the ice crystal size, based on an equation proposed by Ishikiriyama et al. [11] [12] . The radii of ice crystals in the PVA gel were in the range of a few nm to tens of nm depending on the PVA concentration, which was comparable to radii reported by other techniques such as transmission electron microscopy (TEM) [4] .
PVA gels formed from a mixed solvent of dimethylsulfoxide (DMSO) and water had been found to show improved transparency and elasticity compared with PVA hydrogels. Cowie et al. reported the physical properties of viscosity, density, and heat of mixing for PVA with various DMSO/water mixed solvents [13] . Since then, many researchers had investigated the molecular structure and physical properties of PVA, as well as its practical uses. Kaji et al. studied PVA physical gels formed from DMSO/water mixed solvents by neutron scattering and light scattering measurement, showing that the cross-linking points were small crystallites [14] - [17] . They also estimated the average crystallite size and the average intercrystallite distance to be about 7 nm and 15 - 20 nm, respectively.
In this paper, we focused on the melting behavior of solvent crystals in PVA gels prepared from DMSO/water mixed solvents. Rasmussen and MacKenzie reported a phase diagram of temperature and composition ratio for the DMSO/water system [18] . This phase diagram was further investigated in more detail by a number of authors experimentally as well as by computer analysis in order to elucidate the lower-temperature region below about −60˚C [19] - [28] . However, our study restricted the temperature region to temperatures higher than around −60˚C to −70˚C, because the lower-temperature region was very complicated. The melting temperature and enthalpy of ice and DMSO crystals in the PVA/(DMSO/water) gel were measured by differential scanning calorimetry (DSC), and the crystal sizes and weight fractions were discussed on the basis of the phase diagram [15] and crystal nucleation theories [29] [30] .
2. Analytical Background
2.1. Determination of Amount of Solvent Crystals or Freezable Solvent
The amount of freezable solvent―water or DMSO―in the gel (wf) was estimated from the observed heat of fusion of the ice or DMSO crystals. Thus, since the empirical equation for the heat of fusion of a solvent crystal as a function of melting point depression, ΔHm(ΔT), can be obtained or derived from literature reports, the weight
of freezable solvent can be obtained from the observed heat of fusion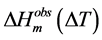 , according to the following equation:
, according to the following equation:
 (1)
(1)
The fraction of freezable solvent in the gel therefore becomes
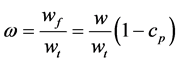 (2)
(2)
where wt is the total weight of freezable and non-freezable solvent, wg is the weight of the gel used in the measurement, and cp is the polymer concentration in the gel.
The empirical equation for the heat of ice in J∙g−1 was given by Randall as a function of the melting point depression [31] :
 (3)
(3)
where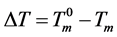 ,
, 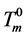 is the equilibrium melting point of ice. Unfortunately, an empirical equation for the heat of fusion of DMSO crystals corresponding to Equation (3) was not available explicitly from the literature.
is the equilibrium melting point of ice. Unfortunately, an empirical equation for the heat of fusion of DMSO crystals corresponding to Equation (3) was not available explicitly from the literature.
The heat of fusion at any temperature T below the equilibrium melting temperature of a DMSO crystal is given as:
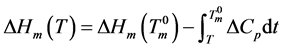 (4)
(4)
where ΔCp is the difference in the heat capacity between the crystal and the undercooled DMSO liquid. These heat capacities at 1 atm as a function of temperature were reported by Clever and Westrum [32] . Using these equations, ΔCp in J∙K−1∙g−1 becomes
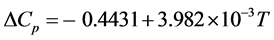 (5)
(5)
From Equations (4) and (5), we obtain
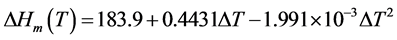 (6)
(6)
where ,
, 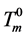 is the equilibrium melting point of DMSO.
is the equilibrium melting point of DMSO.
2.2. Determination of Crystal Size of Freezable Solvent
Assuming the shape of a crystal produced in the gel to be spherical, the radius can be estimated on the basis of the observed melting point depression  from the equilibrium melting point of the crystal (
from the equilibrium melting point of the crystal (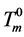 ) [11] . Then, the radius R of the crystal is given by
) [11] . Then, the radius R of the crystal is given by
 (7)
(7)
where γs,l is the interfacial tension between the crystal and the liquid, vm is the molar volume of the liquid, and ΔHm is the molar heat of fusion, which is negative from the definition. This size may be near the critical cluster size for nucleation of the new phase, because the nucleus will immediately be transformed to a crystal below the equilibrium melting point [29] [30] . Here, it should also be noted that when crystallization occurs at the undercooled ΔT, the crystal size can be expressed in the same form as Equation (7), where ΔT should be read as
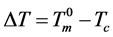 , with Tc being the crystallization temperature [11] [29] [30] .
, with Tc being the crystallization temperature [11] [29] [30] .
The parameters in Equation (7) for water and DMSO, as employed in this study, are summarized in Table 1.
3. Experimental Section
3.1. Materials
Atactic PVA and DMSO were purchased from Wako Pure Chemical Co. Ltd. The degree of polymerization and the degree of saponification of this polymer are 2000 and 98 mol%, respectively. The stereoregularity was determined to be mm = 0.20, mr = 0.51, and rr = 0.29 by 1H NMR measurement, based on assignments by Horii et al. [34] .
3.2. Preparation of Mixed Solvent and PVA Gel
The DMSO/water mixed solvent system was prepared with weight ratios in a range from 0/100 to 100/0. The
![]()
Table 1. Parameters for water and DMSO in Equation (7).
*Tentatively estimated assuming surface energy [33] .
PVA gels were prepared by an alternate freezing and melting method as follows. A PVA solution was prepared in a vessel with a thermostat set at 120˚C for 2 h and then quenched by being placed in another vessel with a thermostat maintained at −10˚C for 20 h. Subsequently, the solution was moved to a vessel with a thermostat set to 25˚C, which was maintained for 4 h. This process was carried out twice in total in order to ensure complete gelation. Measurements were carried out on the resulting PVA/(DMSO/water) gel immediately after preparation to avoid effusion of the solvent from the gel.
3.3. DSC Measurements
DSC measurements were performed using a 8230D calorimeter (Rigaku Co. Ltd., Tokyo). The temperature was calibrated using chloroform and indium. The measurements were carried out under a flow of nitrogen gas, and the samples were sealed in an aluminum pan to prevent evaporation of the solvent. First, the sample was cooled to below −80˚C at a rate of 5˚C/min, and then heated at the same rate. The melting temperature was determined as the starting point of the melting peak on the DSC chart.
4. Results and Discussion
In this study, we first investigated the melting behavior of the water/DMSO system without the polymer, and then we investigated the effect of the PVA gel on this behavior. As the melting behavior of crystals from the mixed solvent is quite complicated, we will provide a brief explanation for the melting point depression of the crystals before describing the results.
According to the phase diagram of the DMSO/water system by Rasmussen and Mac Kenzie, the melting temperature of ice or DMSO crystals caused by phase separation below the equilibrium melting temperature depends on the composition ratio of DMSO to water (DMSO/water) [18] . Thus, as the DMSO fraction increases, the observed melting point of the ice crystals should decrease while that of the DMSO crystals increases, because a crystal is formed at a temperature somewhat below the phase boundary temperature, and its size is near that of the critical nucleus in the nucleation and growth mechanism of phase separation occurring during the cooling process [29] [30] . To provide more detail, the cluster of critical nuclei consisting of pure water or pure DMSO freezes just after phase separation, which occurs under supercooling from the phase boundary temperature; this immediate freezing suppresses further growth of the cluster. This critical size should correspond to the melting point depression.
4.1. Thermal Behavior of DMSO/Water Mixed Solvent
Figure 1 shows the DSC charts of solvent mixtures with various DMSO/water weight ratios. As can be seen in the figure, ice in the pure water system exhibits a normal melting point of 0˚C, which decreases significantly as
![]()
Figure 1. DSC chart of melting behavior of DMSO/water mixed solvent as a function of weight ratio of DMSO to water.
the DMSO fraction increases, up to about 50 wt% DMSO. These melting points are plotted in Figure 2, where the phase boundary curve is indicated by a solid line. The composition dependence of the melting temperature of ice shows similar behavior qualitatively to the phase boundary curve below 50 wt% DMSO, although the magnitude is considerably lower than the boundary temperature. The degree of supercooling is 15 to 25 K in this experiment, which may depend on the cooling rate and the composition ratio of the solvent. This may be elucidated as follows. When the mixed solvent with a given DMSO fraction of less than 50 wt% is cooled below the phase boundary temperature, it should eventually separate into pure ice particles and a homogeneous liquid mixture. However, such phase separation is a competitive process between the nucleation rate of pure water and the cooling rate. With a very small amount of undercooling, the nucleation rate of pure water would be extremely slow, while the size of the critical nucleus is determined by the depression of the boundary temperature from the equilibrium melting temperature of ice. At the usual cooling rate, nucleation occurs at a temperature that is considerably lower than the phase boundary. As is predicted by the nucleation theory of phase separation, the lower the temperature, the smaller the critical size of the nucleation cluster [29] . This critical cluster of pure water freezes soon after phase separation, suppressing further growth. Such small ice particles have a lower melting point due to the effect of surface tension.
The melting behavior of pure DMSO crystals produced in the region above ca. 70 wt% DMSO is also shown in Figure 1 and Figure 2. Figure 2 shows that the melting temperature of pure DMSO crystals increases as the DMSO fraction increases; this tendency seems to follow the phase boundary curve, although the degree of depression from the boundary temperature is quite large. The reason for this has been described above. However, Figure 1 shows another peak at around −70˚C and another at a lower temperature, which are almost independent of the DMSO fraction. These peaks may be assigned as the melting temperature of DMSO crystals with water of crystallization, such as DMSO∙1/2H2O, because the phase diagram shows two horizontal phase boundaries at ca. −70˚C and slightly lower, independent of the DMSO fraction, below which such crystals exist.
Next, we estimated the size of the ice and DMSO crystals from the melting point depression observed in Figure 2 using Equation (7); the results are shown in Figure 3. The crystal size was in a range from 0.5 to 10 nm, and the particle radius of the ice crystals decreased as the DMSO fraction increased, while that of DMSO crystals increased. Judging from the phase diagram, these results are quite reasonable; as was described previously, the phase separation occurs at lower or higher temperatures for ice or DMSO crystals, respectively, as the DMSO fraction increases.
The heat of fusion for ice and DMSO crystals was also examined. The melting enthalpies![]() , estimated from the DSC peak area, were plotted as a function of the DMSO fraction, as shown in Figure 4. The open circles for lower DMSO fractions and the closed circles for greater fractions correspond to the melting enthalpies of ice and DMSO crystals, respectively. From these data, we calculated the weight fraction of these crystals us-
, estimated from the DSC peak area, were plotted as a function of the DMSO fraction, as shown in Figure 4. The open circles for lower DMSO fractions and the closed circles for greater fractions correspond to the melting enthalpies of ice and DMSO crystals, respectively. From these data, we calculated the weight fraction of these crystals us-
![]()
Figure 2. Melting temperature of ice (○) or DMSO (■) crystals as a function of DMSO/water weight ratio. The solid curve shows the phase boundary of the phase diagram by Rasmussen and MacKenzie [15] .
![]()
Figure 3. Radius of ice (○) or DMSO crystals (●) as a function of DMSO/ water ratio in weight, estimated from the melting point depression using Equation (7).
![]()
Figure 4. Melting enthalpy for ice or DMSO crystals measured by DSC. The DMSO/water weight ratios of 0/100 to 50/50 correspond to ice (○), and 70/30 to 100/0 to DMSO crystals (●).
ing Equations (1) and (2). The results are shown in Figure 5, where the symbols have the same meaning as they do in Figure 4. As the weight fraction of DMSO increased, the weight ratio of ice or freezable water to the total amount of water in the system decreased, while that of DMSO crystals or freezable DMSO to the total amount of DMSO increased. Between 47 and 65 wt% DMSO, neither water nor DMSO crystallized. These results are as predicted by the phase diagram above ca. −60˚C.
4.2. Thermal Behavior of DMSO/Water Mixed Solvent in PVA Gel
In the previous section, the thermal behavior of the mixed solvent of DMSO/water was described. Here, we investigate the effect of the PVA gel on this thermal behavior. Both the PVA concentration in the gel and the DMSO fraction were varied from 0 to 100%. For example, DSC charts for various concentrations of PVA gel at a fixed DMSO/water ratio of 19/81 are shown in Figure 6. In this figure, for simplicity, the charts are shown only for PVA concentrations of 0 to 60 wt%, although measurements were also carried out above this concentration. The pure solvent mixture with this DMSO fraction in the absence of PVA showed a melting point of ca. −30˚C, which agrees well with the value shown in Figure 1. Beyond 30 wt% PVA, the melting point shifts to lower temperatures and the degree of the shift increases with PVA concentration. All of the observed melting
![]()
Figure 5. Weight fractions of pure ice (○) and pure DMSO crystals (●), estimated from melting enthalpy ΔH(T).
![]()
Figure 6. DSC charts of melting behavior of PVA gel prepared from a mixed solvent with a fixed DMSO/water weight ratio (19/81) as a function of PVA concentration; only a PVA concentration range of 0 to 60 wt% is shown.
temperatures were plotted as a function of PVA concentration (Figure 7), and the radii of ice and DMSO crystals calculated from these melting temperatures are shown in Figure 8. Both data indicate similar behavior; both the melting point and the crystal size decreased monotonously with increasing PVA concentration. Such behavior is similar to that of PVA hydrogels [9] [10] . The reason for this may be assumed to be as follows. The structure of the solvent―water or DMSO―near PVA chains may be changed because of the strong interaction between them, which means the solvent becomes non-freezable. Hence, an increase in the polymer concentration reduces the amount of freezable solvent. This means that increases and decreases in the DMSO fraction for ice and DMSO crystals, respectively, in the phase diagram, results in larger melting point depressions for these crystals. This idea may be reasonable because the melting enthalpy decreases with increasing PVA concentration. Figure 9 shows the PVA concentration dependence of the melting enthalpy for phase-separated ice or DMSO crystals formed in the gel; the melting enthalpy decreases monotonously with increasing polymer concentration. If these quantities are converted to the weight fraction of the crystals, a nearly completely linear relationship is obtained, as seen in Figure 10. The weight fractions of both ice and DMSO crystals decrease linearly
![]()
Figure 7. Melting temperature of ice (open symbols) or DMSO crystals (closed symbols) plotted against PVA concentration as a function of the DMSO/water weight ratio. DMSO/water = ○: 0/100, □: 19/81, Δ: 38/62, ●: 75/25, ■: 85/15 and ▲: 94/6.
![]()
Figure 8. Radius of ice (open symbols) or DMSO crystals (closed symbols) in the DMSO/water mixture as a function of PVA concentration. DMSO/water = ○: 0/100, □: 19/81, Δ: 38/62, ●: 75/25, ■: 85/15 and ▲: 94/6.
![]()
Figure 9. Melting enthalpy of ice (open symbols) or DMSO crystals (closed symbols) as a function of PVA concentration. DMSO/water = ○: 0/100, □: 19/81, Δ: 38/62, ●: 75/25, ■: 85/15 and ▲: 94/6.
![]()
Figure 10. Weight fraction of ice (open symbols) and DMSO crystals (closed symbols) as a function of PVA concentration. DMSO/water = ○: 0/100, □: 19/81, Δ: 38/62, ●: 75/25, ■: 85/15 and ▲: 94/6.
with increasing PVA concentration; that is, the higher the polymer concentration, the smaller the amount of freezable solvent. In other words, non-freezable pure water or pure DMSO exists in the gel in an amount which increases with the polymer concentration, and finally, at a critical polymer concentration, no freezable solvent exists. It may also be noted here that the slopes of the two lines are significantly different. Specifically, the amount of freezable DMSO decreases more rapidly than the amount of freezable water, corresponding to the difference in the critical concentration above which no freezable solvent exists. These critical concentrations are listed in Table 2.
The fact that the critical concentration of DMSO is considerably lower than that of water suggests that the interaction of DMSO with PVA is much stronger than that of water.
The weight fraction of the solvent crystals or the freezable solvents in Figure 10 was also re-plotted against the solvent composition ratio (DMSO/water) for various PVA concentrations. Figure 11 shows the solvent composition dependence of the solvent crystal (or freezable solvent) fraction for each polymer concentration. The fraction of ice (or freezable water) decreases almost linearly as the DMSO component increases, while the DMSO crystal (or freezable DMSO) fraction increases. This is qualitatively reasonable judging from the DMSO/water phase diagram, which predicts that as the DMSO ratio increases, ice or freezable water decreases and crystal DMSO or freezable DMSO increases. The intercepts of the linear curves with the abscissa provide the critical composition ratios (DMSO/water) above or below which freezable water or freezable DMSO disappears, respectively. Figure 12 summarizes the correlation between the critical PVA concentration and the critical ratio of DMSO/water, which were determined in Figure 10 and Figure 11. Thus, these two critical values depend on each other. For special cases, when a PVA gel is prepared in pure water, the critical PVA concentration above which freezable water disappears is as high as 86.4 wt%, and when prepared in pure DMSO, the value above which no freezable DMSO appears is 50.1 wt%. From this figure, one can obtain simultaneously the critical PVA concentration and the critical DMSO/water ratio above which the whole portion of water becomes completely non-freezable or below which that of DMSO does.
5. Conclusions
The size and weight fraction of solvent crystals (ice or pure DMSO) in PVA gel prepared from a mixed solvent of DMSO/water in various ratios were determined using the melting point depression, compared to their equilibrium melting point, and the melting enthalpy, respectively. These quantities depended on the composition ratio of the mixed solvent and the polymer concentration. The results were elucidated on the basis of a phase diagram reported by Rasmussen and MacKenzie [18] and the theories of nucleation and growth upon phase separation for crystallization, as described by Kelton [29] and ten Wolde and Frenkel [30] .
Under the usual cooling conditions, it was shown that the crystal size was extremely small, a few nm to tens nm, which seemed to be similar to the size of the critical nucleus in the theory of nucleation and growth upon
![]()
Figure 11. Weight fraction of ice (open symbols) or DMSO crystals (closed symbols) plotted against PVA concentration as a function of DMSO/water weight ratio. PVA concentration = ○, ●: 10 wt% gel, □, ■: 20 wt%, △, ▲: 30 wt%, ?, ?: 40 wt%, ◇:50 wt%, and ◎: 60 wt%.
![]()
Figure 12. Correlation between the critical PVA concentration and the critical DMSO/water weight ratio. The former concentration gives the critical value above which neither ice nor DMSO crystals are formed, and the latter ratio provides the critical value above which freezable water does not exist (○), or below which freezable DMSO does not exist (●).
![]()
Table 2. Critical PVA concentrations for various DMSO/water ratios above which freezable water or DMSO does not exist.
phase separation, because they changed along the phase boundary curve with some degree of supercooling. In the PVA gel, these sizes became smaller, which might be due to a strong interaction between the solvent and the polymer molecules. The amount of freezable solvent was reduced to shift the composition ratio in the phase diagram to higher or lower DMSO ratio for ice or DMSO crystals, respectively. Furthermore, the critical condition at which the whole solvent became non-freezable was estimated: this depended on both the PVA concentration and the DMSO/water ratio. The critical PVA concentration for a solvent consisting of pure water was as high as 86.4 wt%, while for pure DMSO it was 50.1 wt%. In a system consisting of pure mixed solvent, with no polymer, there was a composition range between ca. 50/50 and 70/30 in which the solvent became completely non- freezable above ca. −60˚C, as predicted by the phase diagram. Finally, we would like to emphasize that these results were useful for an understanding of the thermal properties of PVA gels prepared from DMSO/water mixed solvents.
Acknowledgements
This work was partially supported by a grant from High-Tech Research Center Program for private universities from the Japanese Ministry of Education, Culture, Sports, Science and Technology.
NOTES
![]()
*Corresponding author.