Sustainability of Wind Energy under Changing Wind Regimes—A Case Study ()
Received 24 January 2016; accepted 26 February 2016; published 1 March 2016

1. Introduction
The public commonly associates climate change with increasing temperatures, changes in precipitation, decreasing glaciers and sea-ice as well as sea level rise. These quantities are of immediate relevance for human life in terms of food production and water availability or in terms of threads to coastal conurbations and agriculture in flatlands. Given these concerns, humankind has searched for other energy sources in an attempt to mitigate climate change. The public sees wind energy as a welcome mean to reduce the fossil fuel usage needed to provide the increasing energy demand due to a growing world population and technology. Currently, 3% of the world’s electricity stems from wind energy; some countries already cover 15% to 30% of their national electricity demand by wind energy [1] .
Since wind-power potential increases with the cube of wind speed, even small changes in wind speed may significantly alter the availability of wind energy [2] . A recent case study over Southeast Alaska revealed that uncertainty in usable wind speeds amounted about 11% due to interannual variability. Uncertainty differed with turbine hub-height, and wind speed itself. Furthermore, the fraction of wind speeds between cut-in and cutout speed differed up to 15% among the examined wind-turbine types (Mitsubischi MWT95/2.4, Clippper Liberty, Gemesa G87-2.0, Siemens SWT 2.3-93, REpower MM92 now Senvion MM92, Vestas V-27, Northwind 100, and Entegrity EW50) [3] . Consequently, predicted average power output showed notable interannual variability with conditions for highest power production at different heights at different times. At 80 m and 30 m hub height, for instance, capacity factors differed about 8% and 5%, respectively, among turbines for the same period, and about 8% and 6% for the same turbine among periods. The ranking among wind turbines of similar hub height with respect to their average power production, however, remained unaffected by these uncertainties [3] .
Renewable energy is a medium- to long-term investment that requires cost-efficiency considerations. For any planned wind farm, its location’s potential power production and capacity factors are assessed for various turbine types prior to decision for a wind-turbine type and construction of a wind turbine (e.g. [4] ). However, in the current decision making process, the sustainability of wind-power generation is not investigated for the site under consideration.
So far, any research on future wind-power potential involved the mid and late 21st century. Analysis by [2] , for instance, suggested that over most of Europe, the changes in wind-power potential under the A1B scenario would remain within ±15% and ±20% by mid and late century, respectively. Their study suggested a tendency towards decreased and increased wind-power potential in the Mediterranean region and over Northern Europe, respectively.
The studies on future wind energy relied on ensembles generated by downscaling data from various climate models by a suit of regional climate models. Here limited area numerical weather prediction (NWP) models have served often to downscale general circulation model simulations, because in NWP, downscaling has improved wind-speed fields. Downscaling of the ERA-Interim or NCEP-NCAR global data to 9 km by the Weather Research and Forecasting (WRF) model [5] , for instance, added significant improvement to wind fields [6] . Note that the current global climate and Earth system models have about similar resolution as the ERA-Interim, and NCEP-NCAR global data.
Due to limited storage capacity, these wind-climate studies relied on simple statistical models to disaggregate stored daily to 3 hourly wind-speed data to account for intra-daily variability in wind speeds [2] . This procedure eliminated uncertainty related to model uncertainties at the cost of uncertainty related to the disaggregation and high frequency changes in wind speeds. However, climate change can cause changes in the frequency of extreme wind speeds and/or calm wind conditions [7] . Both calm wind and conditions above cutout wind speed prohibit wind-energy production.
While these studies on future wind are of great scientific value, for stakeholders or planning of wind farms the mid or end of the 21st century seem light years away. While for wind-energy stakeholders, a warming climate might have positive impacts on wind-energy production in terms of deceased downtimes due to icing, this timescale by far exceeds the lifetime of wind turbines.
However, as climate changes, altered temperature, and moisture conditions may lead to altered horizontal temperature gradients. These changes affect pressure gradients via the equation of state p = ρRdTv (p pressure, ρ density of air, Rd individual gas constant of dry air, 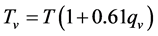 virtual temperature, T air temperature, qv specific humidity). Modified pressure gradients, however, mean changes in wind speed.
virtual temperature, T air temperature, qv specific humidity). Modified pressure gradients, however, mean changes in wind speed.
Over the Pacific Ocean, changes in ocean circulation can intensify or weaken the semi-permanent high- and low-pressure cells and shift their positions. This well-known variability in horizontal pressure gradients occurs on decadal scales. It is expressed by various indices that relate to the strength and position of the winter Aleutian Low. The pressure-gradient decrease between Victoria, Vancouver and Comox, known as the Pacific North American index (PNI), for instance, correlated well with the decreased annual means of 10 m wind speed found in the mid-portion of long-term observations from the late 1940s or early 1950 to the mid-1990s in British Columbia [8] . The decrease in 10 m wind speeds documented itself in increased frequency of calms and reduced frequency of high wind speeds. This reduction also correlated well with the Pacific Decadal Oscillation (PDO) [8] . The PDO was in positive phase for most of 1977 to the mid-1990s when it shifted to negative phase. Positive PDO goes along with above average sea-surface temperatures (SST) off the West Coast of North America, an intensification of the winter Aleutian Low and increased mean wind speeds. The opposite is true for negative PDO. Analysis of 10 m wind-speed data from Thorne Bay, Southeast Alaska, revealed an overall decline in summer 10 m wind speeds since onset of recording in 1990 (Figure 1). Southeast Alaska and adjacent British Columbia have maritime climate that is sensitive to ocean-related variability at the multi-decadal scale.
A recent study [9] summarized observational evidence of declining trends in surface wind speeds over the last five decades in many areas of the World. Decreases in wind speeds have occurred not only in West Canada [8] , but also over the Canadian St. Lawrence Stream region [10] , in the United States [11] [12] , Italian Adriatic region [13] , Australia [14] [15] and China [16] -[18] . Analysis of the North American Regional Reanalysis (NARR) showed increasing wind speeds at wind-turbine height of 80 m over various regions of the contiguous United States [9] .
Given the worldwide, at least regional, evidence for past declining wind speeds in surface observations future sustainability of wind energy requires consideration. The goal of our study was to assess future sustainability of wind-energy production on the scale of the longevity of a wind turbine (~20 y) or wind farm (>20 y) in a region of changing wind regime. To achieve this goal we chose Juneau, Alaska as a testbed for various reasons. 1) The uncertainty of wind-power production due to interannual variability was assessed already for this testbed by means of forecasted wind speeds from evaluated NWP data [3] . This means a known standard exists by which downscaled climate-model data can be assessed with respect to their reliability over a past period. For stakeholders, comparison to a known standard eases the understanding, and helps understanding the uncertainty, which is important for any decision making. 2) Juneau represents a community needing substantial amounts of additional power during the tourist season for cold ironing of cruise ships. Since her major economy depends on summer tourism, clean power demands could increase for environmental protection and mitigation of climate impacts, when all ships would coldiron while at berth in Juneau. 3) Evaluated Community Earth System Model
![]()
Figure 1. Mean 10 m wind speed between May 15 and September 15 for 1990 to 2014 at Thorne Bay, the site with the longest observational record in Southeast Alaska, and at Juneau airport.
(CESM) [19] [20] data [21] downscaled by WRF inline coupled with chemistry (WRF/Chem) [22] [23] existed [24] for the same timeframe used by [3] . These downscaled climatologies were of similar accuracy as climatologies derived from WRF/Chem forecasts [24] . 4) Furthermore, CESM data downscaled by WRF/Chem existed for a seven year timeframe 20 years later [24] than those of [3] from a different project [7] .
2. Experimental Design
2.1. Model Description, Simulations, and Evaluation
For comparability reasons, we assumed the same virtual wind-turbine site as [3] , which is on a single elevation (570 m, 58.374851 N, 134.728506 W) in a wide part of a fjord close to Juneau (see their Figure 1). In our study, we extracted hourly wind-speed data in 80 m height for the length of a tourist season (15 May-15 September) from three different WRF/Chem simulations at the assumed wind-turbine site.
Like multiple years of observations are required to obtain statistics for present climate [7] [25] [26] , several years of downscaled climate projections are needed to separate effects of wind-regime changes from interannual variability. From a theoretical point of view, two independent 30-year climate periods are required to assess changes in climatology [26] . This means 60 years of data are required for a change from one climate period to another. However, the typical lifespan of a wind turbine is about 20 years, which is notably shorter than 60 years. Consequently, we have to look at a smaller time scale than a climate period. Thus, we built our wind “climatologies” based on data of seven seasons that were on average 20 years apart.
To assess sustainability over the lifetime of a turbine, we adopted the comparative approach by [7] . We turned to CESM-RCP4.5 data downscaled with WRF/Chem for the tourist seasons 2006 to 2012 [7] [24] and 2026 to 2032 of [7] [27] . These two datasets are called CESM-P1 and CESM-P2, respectively. They are methodologically consistent as they were produced with the same models with the same setups. Note that the CESM data have a 0.9˚ × 1.25˚ latitudinal and longitudinal, and 6-hour resolution. They stem from the intermediate RCP4.5 [28] simulation that ran in “future mode” after its model year 2005. The RCP4.5 pathway represents a moderate mitigation scenario assuming to reach a 4.5 W∙m−2 climate forcing in 2100.
Wind-farm managers use NWP for forecasting their power production for the next day, up to three days. Thus, they are well familiar with the uncertainty in NWP. For the comparison to their known standard, we included the data by [3] from WRF/Chem simulations run in forecast mode. These simulations used the 1˚ × 1˚, 6-hour resolution National Centers for Environmental Prediction global final analyses (FNL) data [29] for initialization and boundary conditions. This simulation covered the same episode as CESM-P1. However, the simulation ran with the FNL data in forecast mode and the results derived therefrom are called FNL-P1 herafter.
In all these WRF/Chem simulations, the domain encompassed the atmosphere over the eastern Gulf of Alaska, Southeast Alaska and western Canada centered at 58.5 N, 135.5 W with a 7 km increment on 120 ´ 120 grid- points and 28 vertically stretched layers. All simulations used WRF/Chem with the Advanced Research dynamic core [5] with the fully compressible non-hydrostatic prognostic equations of motions and identical model setup.
The WRF-Single-Moment 5-class cloud-microphysics scheme [30] and a further-developed version of the cumulus ensemble scheme [31] served to describe clouds on the resolvable and subgrid-scale, respectively. Shortwave and long-wave radiation were determined by the Goddard two-stream multi-band scheme [32] and Rapid Radiative Transfer Model [33] including cloud and aerosol-radiation feedbacks [34] . Surface and atmospheric boundary layer (ABL) physics followed [35] . The exchange of heat and matter at the atmosphere-surface interface, snow, soil-temperature and soil-moisture and frozen ground conditions were calculated by the NOAH land-surface model [36] in its modified version [5] . The Regional Acid Deposition Model version 2 [37] chemical mechanism [38] used inline calculated photolysis rates [39] . Furthermore, the Modal Aerosol Dynamics Model for Europe [40] and Secondary Organic Aerosol Model [41] were used for aerosol dynamics, physics and chemistry. Activity-based ship- and biogenic emissions were considered in accord with [42] - [44] . Dry deposition followed [45] with the modifications by [49] .
The FNL-P1 and CESM-P1 data for the 2006 to 2012 seasons or subsets thereof were evaluated by different observational datasets and various authors [3] [24] [44] [46] [47] . In the interest of briefness, we summarized their results with respect to wind. The reader is referred to the aforementioned papers for further quantities and details.
The evaluation of the 2008 FNL-P1 simulation by means of 42 surface meteorological sites showed that WRF/Chem overestimated 10 m wind speed at almost all locations, but captured the temporal evolution of wind speed well [47] . Overall bias, root-mean square error (RMSE), and standard deviation of errors (SDE) were 1.75 m∙s−1, 3.34 m∙s−1 and 2.84 m∙s−1, respectively. Slight errors occurred in timing of frontal passages, and due to local effects (channeling, wind shadows, etc.) that were inherent in the observation, but of subgrid-scale with respect to the model. Compared to vertical profiles of wind speeds from 244 radiosonde ascents FNL-P1 overestimated wind speeds less than 1.2 m∙s−1 below 500 m above ground level with RMSEs less than 3 m∙s−1. Looking at all radiosonde ascents and heights, simulated and observed wind speeds correlated 69%, and simulated and observed wind-speed variances agreed well (5.80 m2∙s−2 vs. 5.67 m2∙s−2) [47] .
At the Juneau surface meteorological site, the FNL-P1 10 m wind speeds overestimated the hourly observed values by 1.4 m∙s−1 (2008) to nearly 2 m∙s−1 (2009), and 1.6 m∙s−1 on average with seasonal RMSEs ranging from nearly 3.0 m∙s−1 (2008) to 3.8 m∙s−1 (2009, 2011), and 3.5 m∙s−1 [3] . Evaluation of 10 m wind speeds between cut-in wind speed and the wind speed at rated power revealed that the wind speed with lowest bias differed among years in this range. Note that management of spinning reserves requires high accuracy in this range. Typically, around zero-bias occurred between 4.1 m∙s−1 and 4.6 m∙s−1. Except for 2009, RMSEs were lowest (~2.6 m∙s−1 on average) for 10 m wind speeds between 2.6 m∙s−1 and about 6.1 m∙s−1, and RMSEs increased slightly with increasing 10 m wind speeds after exceeding 5.1 m∙s−1 [3] .
Downscaling of CESM data with WRF/Chem (CESM-P1) can reproduce climatological conditions in Southeast Alaska in summer (JJA) well when compared to climatology from gridded blended sea-wind speeds [24] . Comparison of 10 m wind-speed climatologies gained from downscaling of CESM data by WRF/Chem (our CESM-P1) with those gained from WRF/Chem simulations in forecast mode driven with FNL analysis data (our FNL-P1) suggested similar quality as known from NWP. Over water, the downscaled 10 m wind-speed climatology JJA-bias (simulated minus observed) was −0.7 m∙s−1. The authors [24] suggested that WRF/Chem- downscaled CESM data for future episodes might have similar quality than current NWP if the CESM-assumed future conditions became true.
2.2. Analysis
The wind-turbine types considered in this study were the Enercon E-48, Suzlon S64 Mark II-1.25 MW, General Electric 1.6 - 82.5, Senvion MM92 (formerly known as RE Power MM92), Mitsubischi MWT95/2.4, Enercon E-82 E4, and Siemens SWT-3.6-107. Some of their technical specifications are listed in Table 1. These turbines were chosen as they have rated powers in about 400 kW increments. The Senvion MM92 and Mitsubischi MWT95/2.4 were also used in [3] ’s study on uncertainty in wind-power assessment in complex terrain.
The wind potential was assessed using the same method as in [3] [4] . For each tourist season of the three datasets, we calculated the average power output
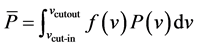 . (1)
. (1)
Here 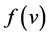 is the probability density function of a given wind speed v occurring during a certain period. It is expressed by the Weibull two-parameter distribution
is the probability density function of a given wind speed v occurring during a certain period. It is expressed by the Weibull two-parameter distribution
![]()
Table 1. Specifications of the wind turbines considered in this study (adopted from [48] ).
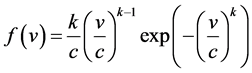 . (2)
. (2)
obtained by fitting the cumulative histogram of the simulated wind speeds. Furthermore, vcut-in and vcutout are the cut-in and cutout wind speeds listed in Table 1. The ratio of the average power output, 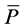 , to the rated power, PR (see Table 1), is the capacity factor
, to the rated power, PR (see Table 1), is the capacity factor
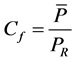 . (3)
. (3)
We discretized the power curves published by the manufacturers when these data were not available. Figure 2 shows the power curves of the turbines. By using the power-curve data, we determined the empirical fitting parameters A, K, Q, B, M, and u of the general logistic function
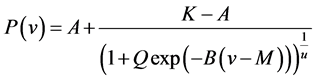 , (4)
, (4)
where  is the power produced by the respective turbine at wind speed v. The results are listed in Table 2.
is the power produced by the respective turbine at wind speed v. The results are listed in Table 2.
Since CESM ran in “future mode” since its model year 2005, downscaled data of the tourist seasons 2006 to 2012 (CESM-P1) correspond to projected climate. On the contrary, the data of FNL-P1 are the weather forecasted for the tourist seasons of 2006 to 2012. Therefore, actual years of FNL-P1 and CESM-P1 are not comparable. However, their statistical characteristics (mean, interannual variability, etc.) should be similar over the seven seasons. Therefore, CESM-P1 wind-power potentials obtained for the seven tourist seasons were compared to those obtained for FNL-P1 to assess whether the mean power output calculated from downscaled
![]()
![]()
Figure 2. Power curves of the wind turbines considered in this study (adopted from [48] ).
![]()
Table 2. Parameters used in the generalized logistic function (Equation (4)) used to model the turbines’ power curves. Values for Senvion MM92 and Mitsubishi MWT95/2.4 are from [4] , the others from [48] .
climate simulations captures the mean power output of the period. Furthermore, this comparison provides stakeholders a reference to their known standard of NWP-derived wind-power potentials.
To assess the long-term reliability of wind speed and sustainability of wind-power production, we compared the mean wind speeds, mean power outputs and the mean capacity factors of the various turbines obtained for CESM-P1 and CESM-P2. Comparison of the interannual variability of the two periods permits assessment of sustainability form year-to-year.
Some prior studies used multi-model means for long-term wind-speed changes and/or 3 h or 6 h means [2] . Therefore, we calculated mean wind speeds for each hour of the seven tourist seasons for each the three datasets. We then compared the period-mean power output obtained from these hourly seven-season mean wind speeds to that obtained by use of all hourly individual wind-speed data of each dataset as well as to the mean power output determined from hourly wind speeds of the individual (model) year’s tourist season.
3. Results
In the interpretation of the results, one has to keep in mind that CESM ran in “future mode” after its model year 2005. Therefore, the CESM-P1 data represent the local wind-speed climate of the tourist seasons 2006 to 2012, and not the actual wind speeds during a particular year. On the contrary, FNL-P1 represents the forecasted 80 m wind speeds of the tourist seasons of 2006 to 2012. Therefore, one can only compare the wind-speed climatologies of the 2006 to 2012 period, but not individual days or years [24] .
The reader should be aware that the WRF/Chem results for the CESM-P2 future period assumed the conditions of the RCP4.5 emission pathway. Thus, the discussion would require the conditional tense. However, for ease of readability, we used the past tense in the following, which we can justify by the fact that the CESM-P2 simulation existed already.
3.1. Wind Speeds
3.1.1. Known Standard FNL-P1
According to FNL-P1, about 80%, 65%, 58%, and 52% of the forecasted wind speeds exceeded 2, 3, 3.5, and 4 m∙s−1, which are the cut-in speeds of the considered turbines (Table 1). About 8%, 7%, 6%, 4% and 2% of the forecasted wind speeds exceeded 11.5, 12, 12.5, 13.5, and 16 m∙s−1, which correspond to wind speeds at rated power for the various turbines. Forecasted wind speeds exceeded 24 and 25 m∙s−1 in less than 0.05% and 0.04% of the total 20,832 hours. In a climatological sense, about 11 and 8 hours, respectively, were lost due to exceedance of the cutout wind speed.
The percentage of wind speeds above cut-in (below rated power) speed differed up to 12% (about 11 to ~14%) among wind-turbine types over the total period and in individual years (Figure 3). For all examined turbines, maximum internannual variability of usable wind speeds amounted ~8% except for the Suzlon S64 Mark II-1.25 MW with slightly over 9%. The probability density of wind speeds up to 3 m∙s−1 varied highest among tourist seasons.
3.1.2. Assessment of Downscaled CESM-P1 Wind Speeds by Known Standard
In CESM-P1, 80 m wind-speed mean and standard deviation were 5.35 ± 3.97 m∙s−1. These values were slightly higher than obtained for the same period in FNL-P1 that were 5.23 ± 3.81 m∙s−1. The frequency of CESM-P1 wind speeds in 1 m∙s−1 bins remained between −0.3 and ~1% of those obtained by FNL-P1 (Figure 3). This finding indicates that CESM-P1 wind-speed climatology had similar quality as the known standard of NWP. According to a two-tailed Student t-test, CESM-P1 and FNL-P1 wind speeds represented the same climatology at the 95% confidence level.
CESM-P1 frequency of wind speeds in bins of 1 m∙s−1 can be approximated as f(v) = −0.0152v3 + 0.879v2 + 16.855v + 108.62 with R2 = 0.9992. This polynomial of third order differed marginally from that obtained for FNL-P1 given by f(v) = −0.0159v3 + 0.9101v2 + 17.258v + 109.23 with R2 = 0.999. Based on these findings, one has to conclude that CESM-P1 represented the wind climatology of known standard well.
Since the CESM-P2 data were derived with the same method as the CESM-P1 data, one may assume similar quality as known from NWP for the CESM-P2 data if the RCP4.5 path were to become true. This means that under these assumptions, wind-farm management can interpret the results with their known experience from NWP.
According to CESM-P1, about 79%, 65%, 59%, and 53% of the downscaled wind speeds exceeded cut-in speeds of 2, 3, 3.5, and 4 m∙s−1, respectively. About 8%, 7%, 6%, 5%, and 2% of the wind speeds exceeded speeds at rated power of 11.5, 12, 12.5, 13.5 and 16 m∙s−1. In only 0.04% (~8 h) and 0.03% (<6 h) of the time, wind speeds exceeded the cutout speed of 24 m∙s−1 and 25 m∙s−1, respectively.
The percentage of wind speeds above cut-in and below wind speed at rated power differed up to 12% and 9% to 16% among wind-turbine types over the total period and in individual years, respectively (Figure 3). The fraction of usable wind speeds differed up to about 20% among tourist seasons for all turbines, except the Suzlon S64 Mark II-1.25 MW and General Electric 1.6 - 82.5. In these cases, the fraction of usable wind speeds varied up to about 26 and 23%, respectively among seasons. Probability density of wind speeds up to 4 m∙s−1 and between 8 and 12 m∙s−1 varied highest among seasons.
FNL-P1 showed lower interannual variability than CESM-P1. It cannot be excluded that the higher variability is an artifact related to spin-up of CESM after switching to “future mode” in model year 2005. The model atmosphere in CESM might not yet have achieved full equilibrium with the “future mode” early in P1. Comparison of the interannual variability of CESM-P1 and FNL-P1 10 m wind speeds at 42 sites with that derived from observations at these sites suggested that both underestimated interannual variability by about half [24] . At these sites, however, CESM-P1 captured interannual variability in 10 m wind speeds better than FNL-P1.
3.1.3. Wind-Speed Change between CESM Data Periods 1 and 2
In CESM-P2, 80 m wind-speed mean and standard deviation were 5.13 ± 3.84 m∙s−1. These values suggested slowing down of mean wind speed and ~3% reduced interannual variability as compared to the 5.35 ± 3.97 m∙s−1 of CESM-P1. The CESM-P2 wind-speed climatology can be approximated as f(v) = −0.0166v3 + 0.9345v2 + 17.37v + 108.11 with R2 = 0.9978. To achieve a 99.9% fit, a fourth order polynomial least squares fit was required (f(v) = 0.0006v4 − 0.0497v3 + 1.4946v2 − 20.76v + 113.29, R2 = 0.9997). According to a two-tailed Student t-test, CESM-P2 and CESM-P1 represented the same wind-speed climatology only at 92% confidence.
The percentage of wind speeds above cut-in and below wind-speed at rated power differed up to 12% and 10% to 14% among wind-turbine types over the total period and in individual years, respectively (Figure 3). The fraction of usable wind speeds differed up to about 10% among tourist seasons for all turbines, except the Suzlon S64 Mark II-1.25 MW and General Electric 1.6 - 82.5. In these cases, the fraction of usable wind speeds varied up to about 13% and 12%, respectively among seasons. Compared to CESM-P1 these findings mean that interannual variability in usable wind speeds and sensitivity to wind-turbine type would decrease by half.
Wind-energy generation increases as the frequency of wind speeds in the range between cut-in and wind speed at rated power increases. Investigation showed decreased frequency of wind speeds in the entire range. The highest reduction occurred around cut-in speed (~3% absolute). Decreases around rated power were less than 1% (Figure 3). In CESM-P2, about 79%, 63%, 56%, and 50% of the anticipated future wind speeds exceeded the cut-in speeds of 2, 3, 3.5, and 4 m∙s−1, while about 8%, 7%, 6%, 4%, and 2% exceeded the wind-speeds at rated power of 11.5, 12, 12.5, 13, and 16 m∙s−1, respectively. Compared to CESM-P1, cut-in speeds of 2, 3, 3.5, and 4 m∙s−1 would be reached about 1, 2, 2, and 3% (absolute) less often. Projected wind speeds always remained below 24 m∙s−1 meaning no loss due to exceeding the cutout wind speed.
In CESM-P2, probability density of wind speeds up to 2 m∙s−1 varied highest among seasons. Compared to CESM-P1, the interannual variability shifted towards lower wind speeds and decreased for wind speeds between 8 and 12 m∙s−1 (cf. Figure 3).
Calculation of a period-temporal evolution of hourly mean wind speeds led to a significantly different wind- speed probability distribution despite of the same mean wind speed (cf. Figure 3(e)). This result was because extremes in low and high wind speeds cancelled each other out. The resulting distribution became nearly Gaussian and peaked at different speeds than those based on individual hourly wind speed values (cf. Figure 3(d)). This finding was not surprising as wind energy is an extensive quantity [26] . Thus, one has to conclude that climate-mean wind speed values cannot be deployed for future wind-power production studies.
3.2. Power Output
Recall that one cannot compare individual years of FNL-P1 and CESM-P1 in a paired mode [24] . The former namely represents results based on weather forecasts in the actual years. On the contrary, the latter represents results based on downscaled climate projections. Consequently, power outputs for CESM model years differed from those of the actual years (Figure 4(a)). However, on temporal mean over the period 2006 to 2012, the wind-speed climatology of CESM-P1 should represent that of FNL-P1. As discussed above, the latter was true with more than 95% confidence (Figure 3(d)).
The average power output gives the potential of the site for a wind-turbine type. In FNL-P1, interannual variability in power output was about 27%. In CESM-P1, tourist seasons showed notable (up to 66%) differences in annual average power output (Figure 4(a)). Due to the different technical data (Table 1), the mean power output over the seven tourist seasons differed among turbines (Figure 5(a)). The interannual variability left the ranking among wind turbines unaffected (not shown), which agreed with the findings for FNL-P1. This finding also confirmed [3] ’s results found for a different suit of turbines using the FNL-P1 wind-speed data.
For the various turbine types, CESM-P1 and FNL-P1 provided nearly the same mean power output over the 2006-2012 period (Figure 5(a)). Compared to known standard, CESM-P1 interannual variability in wind speeds was slightly enhanced (Figure 3(a), Figure 3(b)). Consequently, CESM-P1 interannual variability in tourist-season mean power output exceeded that of the known standard (Figure 5(a)). As mentioned above, CESM started running in “future mode” in model year 2005. Thus, one cannot exclude that oscillation of CESM related to switching modes enhanced interannual variability in estimated power output in CESM-P1.
Using all tourist-season hourly wind speeds to determine the mean power output of a period (e.g. P1) provided the same means than averaging over the mean power outputs of the individual tourist seasons (Figure 5(a), Figure 5(b)). The main advantage of the first-mentioned method is its reduced computational burden. Its main disadvantage is that it eliminates the possibility to assess interannual variability. However, knowledge of interannual variability may be of great value in the decision for, planning of and managing of a site.
Using period-mean values to calculate the period-mean power output significantly underestimated the power output (cf. Figure 5(c)). As aforementioned, extremes in low and high values cancelled each other out leading to a nearly Gaussian distribution of wind-speed probabilities. Energy and power are extensive quantities, which scale with the system’s size, in this case, the magnitude of wind speeds. Consequently, mean values of wind speed can only hint at the direction of change in power output, but fail to provide the magnitude. However, stakeholders need the magnitude to determine the percentage of change and scale to known standard. The authors are well aware of this fact and the results were shown for completeness only.
Comparison of CESM-P1 and CESM-P2 showed a decrease of power output by about 8% for all turbine types over their lifetime (Figure 5(a), Figure 5(b)). This means that (a) future development should focus on improved turbines to make up for the loss in usable wind speeds, and (b) wind-power provider would have to add turbines to sustain the mean amount of wind-energy production if the assumed RCP4.5 conditions of CESM-P2 were to become true.
![]()
![]() (a) (b)
(a) (b)
Figure 4. (a) Exemplary illustration of interannual variability in power output as obtained for the Senvion MM92 split up by individual years for 2006 to 2012 as obtained from wind speeds forecasted by WRF/Chem using FNL analysis data (FNL-P1), and by model years 2006 to 2012 downscaled by WRF/Chem using CESM-projected climate (CESM-P1). Note that interannual variability for other turbines looked similar (therefore not shown). (b) Power output split up by CESM model years 2026 to 2032 downscaled by WRF/Chem using CESM-projected climate (CESM-P2).
Interannual variability in wind-power output was about 30% for CESM-P2. This value agreed well with that of FNL-P1 (~27%), i.e. the known standard. Compared to CESM-P1, however, interannual variability in power output would decrease by 50% in CESM-P2. If this reduction were true, it would mean that power output would be more sustainable from one year to the next in about 20 years.
In summary: The period-mean power output determined for CESM-P1 represented the power output of the period well as compared to known-standard (FNL-P1). The downscaled CESM data (CESM-P1) might lead to an overestimation of the interannual variability in power output. The analysis demonstrated that high-temporal resolution wind-speed data are required for quantitative assessment. Mean values permitted only a qualitative assessment of increase or decrease. At the virtual testbed site, wind-power output would decrease by about 8% over the 20 y lifetime of a turbine. Unfortunately, a reliable statement on changes in interannual variability cannot be made as it cannot be excluded nor proved that the much higher interannual variability in CESM-P1 than FNL-P1 80 m wind speeds is due to spin-up after switching to “future mode” in CESM.
3.3. Capacity Factor
The capacity factor gives the maximal ability of a wind turbine at a site. Figure 6 displays the average capacity factors valid over the three periods. The capacity factors varied among turbines due to the different technical data (Table 1). At the testbed of this case study, period-mean capacity factors ranged from ~16% to 23% for FNL-P1. These values had an interannual variability of up to ~6%. These results well agreed with those found for a different suit of turbines by [3] . The General Electric 1.6 - 82.5 and Senvion MM92 had the highest and second highest capacity factor, respectively (Figure 6).
Comparison to known standard (FNL-P1) suggested about the same capacity factors (~17% to 24%) for the various turbines at this site for the downscaled CESM data (CESM-P1) (Figure 6). Thus, one has to conclude that downscaling of CESM data provided reliable assessment of capacity factors for the past period. With the same argumentation as in Section 3.1, one can assume that the same would be true, if the RCP4.5 conditions assumed in CESM-P2 were to become true.
In CESM-P2, capacity factors ranged between about 15% and 22%, i.e. they were slightly reduced as compared to CESM-P1 (Figure 6) because of the shift in wind-speed probability-density distribution. In CESM-P2, capacity factors showed less interannual variability than in CESM-P1 as well. Again, for the aforementioned reasons, a reliable statement on changes in interannual variability in capacity factors cannot be made. However, if interannual variability in capacity factors would go down, this change would reduce uncertainty in the choice
of the wind turbine with maximal ability at a site. This fact would facilitate the process of adding turbines to sustain wind-power production.
4. Conclusions
Wind farms are long-term investments built to provide clean energy at time scales of 20 years or so. Thus, wind-energy providers are not only interested in assessment of the potential energy production under current conditions, but also in the sustainability of the production over the lifetime of a wind turbine/farm.
Our study presented a method of how to assess the sustainability of wind energy at a site on the scale of the lifetime of a wind turbine. From a theoretical climate science point of view, two independent 30-year climate periods are required to assess changes in climatology [26] [27] . In this scenario, 60 years of wind-speed data would serve to provide a projected wind-speed change. However, a timescale of 60 years is three times the 20 y lifetime of a wind turbine. To consider this smaller timescale, we built our climatologies based on data of seven tourist seasons that were on average 20 years apart.
In doing so, climate projections with CESM for the RCP4.5 pathway were downscaled by WRF/Chem for the tourist seasons of 2006 to 2012 (CESM-P1) and 2026 to 2032 (CESM-P2). We used a virtual site close to Juneau, Alaska as a testbed as this region is known to experience decadal changes in wind regimes due to changes in the circulation of the Pacific Ocean.
In CESM-P2, 80 m wind-speed mean and standard deviation were 5.13 ± 3.84 m∙s−1. These values suggested slowing down of mean wind speed and ~3% reduced interannual variability as compared to the 5.35 ± 3.97 m∙s−1 of CESM-P1. Compared to CESM-P1, cut-in speeds of 2, 3, 3.5, and 4 m∙s−1 would be reached about 1, 2, 2, and 3% (absolute) less often. Wind speeds at rated power would decrease by less than 1%.
Comparison of CESM-P1 and CESM-P2 at the testbed showed a decrease of power output by about 8% for all turbine types over their lifetime under RCP4.5 conditions. This finding leads to the conclusion that (a) future development should focus on improved turbines to make up for the loss in usable wind speeds, and (b) wind- power provider would have to add turbines to sustain the mean amount of wind-energy production if the assumed conditions of CESM-P2 were to become true.
Comparison to known standard of wind speeds from numerical weather prediction (FNL-P1) suggested about the same capacity factors for the various turbines at this site for the downscaled CESM data (CESM-P1). Therefore, one can conclude that downscaling of CESM data provided reliable assessment of capacity factors for the past period. The known standard of forecasted winds permits stakeholders to understand the uncertainty of projected changes at least with respect to uncertainty related to the model. Further non-accounted uncertainty, of course, exists due to assumptions on the pathway of climate forcing.
It was demonstrated, that climate-mean values of wind speed can provide a board idea of changes in wind regimes as such, and the direction of power production in qualitative terms (decrease/increase). However, they fail to provide quantitative assessment of changes in wind-power production, as energies are extensive quantities, i.e. the power production depends on the actual size of wind speed. As such, power has to be calculated at the scale of the actual wind-speed distribution and not its mean distribution. Stakeholders, namely, need the magnitude of change and a comparison to known standard. The former serves to scale the current actual power production to determine its sustainability over the lifetime of a turbine/wind farm to take appropriate actions. The latter provides the stakeholders with a good sense for the uncertainty of the projected change.
Acknowledgements
We thank the anonymous reviewers for fruitful discussion and helpful comments. The WRF/Chem simulations were performed within the framework of the National Park Service grant (contract P11AT30883/P11AC90465). The Research Support Center at the Geophysical Institute provided HPC time and storage space for the simulations.