The Assessment of Groundwater Vulnerability Due to Leaching of Chemicals: The Review of Attenuation Factor ()
Received 24 December 2015; accepted 23 January 2016; published 26 January 2016

1. Introduction
Chemical fate and transport models are used to assess groundwater vulnerability due to leaching. There are three types of models. They are index based models, processed based models, and statistical based models. The index based models which exclude important processes and are conceptual are used for preliminary investigations, as they are not data intensive. Due to its simplicity, the index based models are useful specifically in relative vulnerability assessments based on relative or reference chemicals whose leaching behaviors are known from field/experimental/modeling studies [1] - [6] . Most of the index based models are based on attenuation factor (AF) approach that is coupled with Geographical Information System (GIS). Therefore, the objective of this paper is to review the research works done using the AF approach to outline the future research needs.
2. The Approach of Attenuation Factor (AF)
AF, which ranges between 0 and 1, is defined as the fraction of the pesticide that goes to groundwater table (GWT). For example, referring to Figure 1, if 100 units of pesticide A is applied at the ground surface, as per AF approach, it is expected 0.6 × 100 units to reach the GWT.
In AF approach, as shown in Figure 2, the groundwater system is divided into two zones. They are root zone and intermediate vadose zone. Within each zones, under the assumption that the pesticides degrade following a first-order kinetics, the total amount of pesticide leaching out a zone is calculated using Equation (1’’’’) [1] .
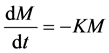 (1)’
(1)’
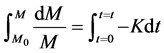 (1)’’
(1)’’
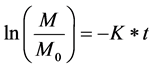 (1)’’’
(1)’’’
 (1)’’’’
(1)’’’’
![]()
Figure 1. The approach of attenuation factor.
![]()
Figure 2. The schematization of soil profile in attenuation factor.
where M, M0, t and K are mass leaching past the zone, mass entering the zone, the travel time and the first-order degradation coefficient, respectively. Assuming that , as per Equation (1’’’’) and Figure 2, the amount of pesticide entering the groundwater table (M2) is given by Equation (2’’’’).
, as per Equation (1’’’’) and Figure 2, the amount of pesticide entering the groundwater table (M2) is given by Equation (2’’’’).
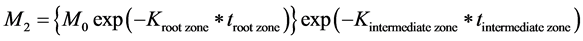 (2)’
(2)’
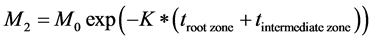 (2)’’
(2)’’
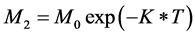 (2)’’’
(2)’’’
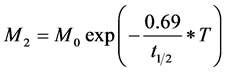 (2)’’’’
(2)’’’’
where 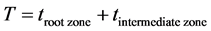 is the total travel time and
is the total travel time and 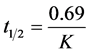 is the half-life time of the applied pesticide
is the half-life time of the applied pesticide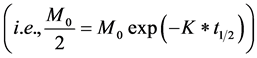 .
.
Considering that the total travel time (T) is approximately equal to , the mathematical expression of AF approach is given by Equation (3) [1] . The term “RF” that is known as retardation factor is defined by Equation (4).
, the mathematical expression of AF approach is given by Equation (3) [1] . The term “RF” that is known as retardation factor is defined by Equation (4).
![]() (3)
(3)
![]() (4)
(4)
where d, ϑ, q, t1/2, ρ, f, and K are depth to groundwater table (m), moisture content at field capacity, recharge rate or average water flow rate through soil (m/day), half-life time of the applied pesticide (days), bulk density (kg/m3), faction of organic carbon content, and soil organic carbon sorption coefficient (m3/kg), respectively.
3. Implication of Skewness of AF Values
With the analysis of available data, [2] found that the computed values of AFs are highly skewed for a given pesticide (DBCP) under different soil conditions. As per [2] , the distribution of highly skewed AFs may not suit for proper estimation of variance and probability assessment. Furthermore, [2] has also found that the computed value of mean AF and the uncertainty interval for a reference chemical fall within the uncertainty interval of the other reference chemical, so that the discrimination of chemicals with respect to reference chemicals becomes infeasible. Therefore, a new equation, which is known as Revised Attenuation Factor (AFR) and approaches normality, has been proposed as given in Equation (5’-5’’). The constant “k” insures that AFR has a value greater than unity [2] .
![]() (5)’
(5)’
![]() (5)’’
(5)’’
4. Leaching of Volatile Organic Compounds (VOC) on AF Values
VOCs are a group of chemicals with high vapor pressures, which can cause public health risk. Ki and Ray [3] has found that the Equations (1-4) don’t account for VOCs. Therefore, as shown in Equations (6-7), few additional terms (i.e., vapor-phase partitioning for RF and volatilization loss for AF) are introduced. The Equation (6) and Equation (7) are known as Expanded Attenuation Factor (EAF) and Expanded Retardation Factor (ERF), respectively.
![]() (6)
(6)
![]() (7)
(7)
where![]() , l, and n are the gas diffusion coefficient in soil (m2/day),dimensionless Henry’s constant, thickness of stagnant boundary layer above ground surface (m), and air-filled porosity, respectively.
, l, and n are the gas diffusion coefficient in soil (m2/day),dimensionless Henry’s constant, thickness of stagnant boundary layer above ground surface (m), and air-filled porosity, respectively.
5. Implication of Input Uncertainty on AF
Though the index based models are the simplest in assessing the groundwater vulnerability due to leaching of chemicals, the index based models are associated with input uncertainties such as uncertainties in soil properties (e.g., θ and ρ), climate (e.g., q), and pesticide properties (e.g., t1/2). Therefore, there is a need to associate an error band on AF. As per [2] [4] , assuming that the inputs to AF approach are not correlated among themselves, non-correlated first order uncertainty is applied to produce an error band (![]() ) on AF. The non-correlated first order uncertainty is given by Equation (8).
) on AF. The non-correlated first order uncertainty is given by Equation (8).
![]() (8)
(8)
where ![]() is the coefficient of variation for parameter/input “i”. For example, considering
is the coefficient of variation for parameter/input “i”. For example, considering![]() , one of the parameters in Equation (3),
, one of the parameters in Equation (3), ![]() is given by
is given by ![]() where
where ![]() denotes the standard deviation of
denotes the standard deviation of![]() . It is noted that RF that is defined by Equation (4) is one of the parameters in Equation (3), and depends on many parameters (i.e., ϑ, ρ, f, and K). Therefore, the coefficient of variation of RF is also computed using the concept of non-correlated first order uncertainty.
. It is noted that RF that is defined by Equation (4) is one of the parameters in Equation (3), and depends on many parameters (i.e., ϑ, ρ, f, and K). Therefore, the coefficient of variation of RF is also computed using the concept of non-correlated first order uncertainty.
Loague et al. [4] found that higher categories of soil taxonomy have the tendency to increase the uncertainty in the estimate of mean soil properties. As per Equation (8), larger individual component uncertainties increase the uncertainty in the computed value of AF. Therefore, [4] concludes that the uncertainty in the computed value of AF increases if one needs to use the estimate of mean soil properties in higher categories of soil taxonomy, in the absence of mean soil properties in lower categories of soil taxonomy. Based on the testing of correlations among soil properties of Rhodic Eutrustoxsoil, [2] concludes that the assumption that the variables in the AF approach are not correlated results in an inflated estimate of![]() , but the differences between the correlated and not correlated results are not that significant.
, but the differences between the correlated and not correlated results are not that significant.
6. Classification of Chemicals Using Reference Chemicals as Leachers and Non-Leachers
The concept of reference chemicals are introduced for the purpose of relative vulnerability assessments. The reference chemicals are the pesticides whose leaching behaviors are known under local conditions based on field/experimental/modeling studies, and that have sufficiently different mean AFRs and low standard deviations [2] . For example, as shown in Figure 3, selecting the chemicals shown in Case3 as reference chemicals may lead to better discriminate the chemicals [2] , where the circles and arrows represent the mean AFRs and the uncertainty intervals of the reference chemicals, respectively.
The reference chemicals are used to categorize the pesticides as “leachers” or “nonleachers”. To illustrate the method of categorization using the concept of reference chemicals, few chemicals with the associated AFR values in Rhodic Eutrustox soil are placed in Table 1. In categorizing the chemicals using the normalized AFR values and the reference chemicals, at first, the means of the reference chemicals are assigned either “−1” or “1”. For the chemicals shown in Table 1, DBCP (leaching reference chemical with an AFR value of 3.12) and Diuron (nonleaching reference chemical with an AFR value of 6.03) are considered as reference chemicals and assigned −1 and 1, respectively.
The midpoint between these two points (i.e., between −1 and 1) becomes the origin of the normalized axis, and the distance between the origin and either of the two normalized means is assigned one unit in the normalized axis [2] . With these definitions, as shown in Figure 3, the AFR of the origin in the normalized axis is
![]()
Figure 3. The selection of reference chemicals.
![]()
Table 1. Computed AFR values in Rhodic Eutrustox soil [2] .
found to be![]() . In other words, a unit value in the normalized axis is equal to 1.46 us
. In other words, a unit value in the normalized axis is equal to 1.46 us
ing the AFR value. Then for any chemical of interest that need to be categorized based on reference chemicals, its means and standard deviations are converted to normalized scale. For example, as shown in Figure 4, the
normalized mean of Anilazine is![]() . The arrows represent the uncertainty intervals (+/−
. The arrows represent the uncertainty intervals (+/−
normalized standard deviations) for the chemicals. As shown in Figure 5 and Figure 6, this same procedure is followed for Dicamba and Ametryn.
The classification of the selected chemicals (i.e., Ametryn, Dicamba, and Anailazine) with respect to the reference chemicals (i.e., DBCP and Diuron) is shown in Figure 7. With this classification system, Ametryn and Anailazine are considered as nonleaching chemicals, whereas Dicamba is considered as a leaching chemical.
7. Determination of Input Data for AF Computation
Though AF approach is an index based model, the accurate prediction of AF heavily relies on some site specific data. As reported in the literature [5] , soil parameters (e.g., ϑ and ρ) are obtained through field samples at different depths up to 20 cm depth from the ground surface to obtain the average value for the mentioned soil parameters. Subsequently, it is assumed that these average values for soil parameters represent the soil up to GWT. As per [5] , the depth to GWT doesn’t influence the groundwater vulnerability assessment. Therefore, d is set to 0.5 m in most of the studies. Laboratory experiments are conducted to estimate the soil organic carbon sorption coefficient [6] .
8. Sensitivity Analysis
Mathematical models are used to understand the complex phenomena. Therefore, the determination of model parameters that are most influential on model results is one of the important phases in model development. Oftentimes, the parameters that are most influential are identified through a sensitive analysis.
Based on a sensitive analysis of parameters using Latin-Hypercube-One-factor-At-a-Time (LH-OAT) method, [3] found that the parameters rank from top to bottom in the order of K, f, d, q, and t1/2. For this study, the samples are obtained from 10 equiprobable intervals in a 11-dimensional parameter space for a loop of 10,000 iterations. This study also concludes that the AF approach is least sensitive to parameters such as ϑ and ρ.
9. The Accuracy of AF Approach against Numerical Models
As underscored in the literature [3] , STANMOD (STudio of ANalytical MODels) and HYDRUS-1D models are
![]()
Figure 4. The normalized AFR of anailazine in Rhodic Eutrustox soil.
![]()
Figure 5. The normalized AFR of dicamba in Rhodic Eutrustox soil.
![]()
Figure 6. The normalized AFR of ametryn in Rhodic Eutrustox soil.
![]()
Figure 7. The classification of pesticides in Rhodic Eutrustox soil.
widely used to compare the outcome of AF approach.
STANMOD is designed to analyze solute transport in soils using analytical solutions of convection-dispersion solute transport equation [7] [8] . The users of STANMOD have several options such as CHAIN, CFITM, CFITIM, CXTFIT, and SCREEN, to select a specific program to be used to solve analytical solutions of convection- dispersion solute transport equation. Among these options, SCREEN is used to classify and screen organic chemicals for their relative susceptibility to different loss pathways in soil and air. The loss pathways could be in the form of volatilization, leaching, and degradation. The SCREEN model assumes linear, equilibrium partitioning between vapor, liquid, and adsorbed chemical phases, net first order degradation, and chemical losses to the atmosphere by volatilization through a stagnant air boundary layer above the soil surface [7] [8] . Most of the parameters (e.g., d, ϑ, q, t1/2, ρ, f, and K) used in STANMOD are the same as in AF approach. Some of the parameters such as chemical properties (e.g., K and t1/2) come from an in-built database that is taken from [9] . However, in STANMOD, the model parameters are not associated with uncertainty levels as in AF approach.
On the other hand, HYDRUS-1D is an interactive model for simulating one-dimensional water flow, heat transport, and solute movement in variably saturated soils (i.e., between the groundwater surface and the ground water table). In HYDRUS-1D, the water flow is modeled by Richards’ equation. The solute movement and heat transport are modeled through Fickian-based advection-dispersion equation [10] [11] . The soil hydraulic properties are described analytically by the methods of van Genuchten, or Brooks and Corey [10] [11] . The governing equations for water flow, heat movement, and solute transport are solved using Galerkin-type linear finite element schemes [10] [11] . The model is setup by selecting the processes (i.e., water flow, heat, and solute transport) to be simulated, specifying the spatial and temporal scales, and setting the initial/boundary conditions. The model is also packaged with a post-processing unit to visualize the simulation results in the form of charts or graphs of parameters such as soil hydraulic properties and concentration profiles. The recent advancement of the model has also provided a platform to couple with MODFLOW (a modular finite-difference groundwater model). HYDRUS provides MODFLOW with recharge fluxes into groundwater, while MODFLOW provides HYDRUS with the position of the groundwater table that is used as the bottom boundary condition in HYDRUS [10] [11] .
10. The Application of AF Approach
In this section, the computation of AF approach is explained by selecting a soil in the state of Hawaii. The statistical properties of the soil and the chemical (i.e., Diuron) are placed in Table 2. The given soil properties re- present the top 20 cm from the ground surface.
Based on the values of the parameters presented in Table 2, and by using Equation (3) and Equation (4), the values of RF and AF are calculated as shown below:
![]()
![]()
![]()
![]()
As discussed previously, in AF approach, the inputs are associated with uncertainties. The uncertainty levels of the inputs are represented through the given standard deviations (Table 2). To associate an error band on AF, at first, the value of![]() ,which is an error band on RF, as shown below, is computed using non-correlated first order uncertainty analysis discussed in Section 5.
,which is an error band on RF, as shown below, is computed using non-correlated first order uncertainty analysis discussed in Section 5.
![]()
![]()
![]()
![]()
Table 2. The statistical properties of the soil and the chemical (i.e., Diuron) [4] .
*SD: Standard Deviation; d = 0.5 m ± 0.25 m; t1/2 = 27.5 days ± 43.8 days; q = 0.001 m/day ± 0.0005 m/day.
![]()
![]()
The computed value of ![]() is used in the non-correlated uncertainty analysis of AF.
is used in the non-correlated uncertainty analysis of AF.
![]()
![]()
![]()
![]()
![]()
11. The Implementation of AF Approach Using MATLAB
MATLAB® is a high-level language and an interactive environment for numerical computation, visualization, and programming. More than a million engineers and scientists in industry and academia use MATLAB to analyze data, develop algorithms, and create models and applications [12] . Therefore, the implementation of AF approach is outlined through MATLAB programming language. The source code is given below. The detail about the language syntax is available from [12] .
In the given source code, within the mainFunction(), few global variables are declared to store the input data for the AF approach. The input data is read from a user specified spreadsheet. The input data has the mean and the standard deviation of the variables (e.g., d, ϑ, q, t1/2, ρ, f, and K) that are used in the AF approach as explained in Section 2.0. The assignments of the global variables are carried out within the function named assignVariables(). Having assigned the variables, the computation of AF and RF are performed by calling the function named computeAFRF(). To compute the standard deviations of AF and RF, two functions namely computeSDAF() and computeSDRF() are called within the mainFunction(). These functions are used to compute the CV values, as discussed in Section 5.0, for each of the variables (e.g., d, ϑ, q, t1/2, ρ, f, and K) that are used in the AF approach. The final outcomes (i.e., values of AF, RF, and standard deviations of AF and RF) of the simulation are stored in a spreadsheet that can be visualized using one of the GIS software.
%Declaration of global variables
%Reading from a worksheet
%Calling of functions
function mainFunction()
global AFData RF AF SDRF SDAF;
global Density SDDensity f SDf Theta SDTheta K SDK q SDq Halflife SDHalflife d SDd;
AFData = readtable('afinput.xlsx','Sheet','parameters');
assignVariables();
computeAFRF();
computeSDRF();
computeSDAF();
writeOutput(RF,SDRF,AF,SDAF,'afoutput.xlsx');
displayGraph(RF,SDRF)
end
%Assignment of variables
function assignVariables()
global AFData;
global Density SDDensity f SDf Theta SDTheta K SDK q SDq Halflife SDHalflife d SDd;
Density = AFData{:,{'Density'}};
SDDensity=AFData{:,{'SDDensity'}};
f=AFData{:,{'f'}};
SDf=AFData{:,{'SDf'}};
Theta=AFData{:,{'Theta'}};
SDTheta=AFData{:,{'SDTheta'}};
K=AFData{:,{'K'}};
SDK=AFData{:,{'SDK'}};
q=AFData{:,{'q'}};
SDq=AFData{:,{'SDq'}};
Halflife=AFData{:,{'Halflife'}};
SDHalflife=AFData{:,{'SDHalflife'}};
d=AFData{:,{'d'}};
SDd=AFData{:,{'SDd'}};
end
%Computation of AF and RF
functioncomputeAFRF()
global RF AF ;
global Density SDDensity f SDf Theta SDTheta K SDK q SDq Halflife SDHalflife d SDd;
RF=1+Density.*f.*K./Theta
AF=exp(-0.69.*d.*RF.*Theta./q./Halflife);
end
%Computation of standard deviation of RF
function computeSDRF()
globalAFData;
global SDRF;
global Density SDDensity f SDf Theta SDTheta K SDK q SDq Halflife SDHalflife d SDd;
CVTheta=-1.*Density.*f.*K./(Theta.^2).*SDTheta;
CVDensity=f.*K./Theta.*SDDensity;
CVf=Density.*K./Theta.*SDf;
CVK=Density.*f./Theta.*SDK;
SDRF=(CVTheta.^2+CVDensity.^2+CVf.^2+CVK.^2).^0.5
end
%Computation of standard deviation of AF
function computeSDAF()
global AFData;
global Density SDDensity f SDf Theta SDTheta K SDK q SDq Halflife SDHalflife d SDd;
global RF AF SDRF SDAF ;
CVd=(-0.69.*RF.*Theta./q./Halflife).*exp(-0.69.*d.*RF.*Theta./q./Halflife).*SDd;
CVRF=(-0.69.*d.*Theta./q./Halflife).*exp(-0.69.*d.*RF.*Theta./q./Halflife).*SDRF;
CVTheta_AF=(-0.69.*d.*RF./q./Halflife).*exp(-0.69.*d.*RF.*Theta./q./Halflife).*SDTheta;
CVHalflife=(0.69.*d.*RF.*Theta./q./(Halflife.^2)).*exp(-0.69.*d.*RF.*Theta./q./Halflife).*SDHalflife;
CVq=(0.69.*d.*RF.*Theta./(q.^2)./Halflife).*exp(-0.69.*d.*RF.*Theta./q./Halflife).*SDq;
SDAF=(CVd.^2+CVRF.^2+CVTheta_AF.^2+CVHalflife.^2+CVq.^2).^0.5;
end
%Write to a worksheet
function writeOutput(RF,SDRF,AF,SDAF,OutputFilename)
OutputTable = table(RF,SDRF,AF,SDAF);
writetable(OutputTable,OutputFilename,'Sheet',1)
end
%Display the graph
function displayGraph(RF,SDRF)
plot(1:3,RF,'g--O', 1:3,SDRF,'--*');
xlabel('Soil Taxonomy Order');
ylabel('RF or Standard Deviation of RF');
legend('RF','Standard Deviation of RF','Location', 'southeast');
end
12. Future Research
Based on the reviewed papers, the following points are highlighted:
1) In AF approach, the groundwater recharge/average water flow rate through soil (q) requires a constant value. Therefore, it is unclear about the time scale (i.e., daily, monthly, or yearly) of the groundwater recharge. Moreover, with the current approach of AF with a constant value of groundwater recharge, it is not feasible to evaluate trends and strengths of attenuation of chemicals over time and space, which can help to determine if the pollutant levels have declined or increased with time in space.
2) A value of zero for RF implies that the applied pesticide is not lost due to sorption. In other words, at RF = 0, AF = 1. Thus, all the applied pesticide reaches the GWT regardless of half-life time of the applied pesticide.
3) In the literature, it has been concluded that the depth to GWT does not have an influence on the groundwater vulnerability assessment. Therefore, the uncertainty associated with the value of depth to GWT is set to zero. These conclusions may not be concrete in spatial context as well at a given location.
4) As per the definition of AF, it is expected to have x*AF mg at the groundwater table, if the AFs of two pesticides that are applied at a rate of x mg are the same. Under this scenario, the outlined classification system based on reference chemicals will not work. This is owing to the fact that the classification system based on reference chemicals does not consider the acceptable levels of the pesticides at the groundwater table.
5) [13] has developed a spatial evapotranspiration tool (SET) that can geographically encompass all the best available climate datasets to estimate evapotranspiration (ET) using Penman-Monteith method [14] [15] at different spatial/grid scales. This spatial tool is developed as a Python toolbox in ArcGIS using Python, an open source programming language, and the ArcPysite-package of ArcGIS. Therefore, with the availability of remotely sensed (e.g., MODIS/NEXRAD/PRSIM) and land-based climate data, the possibility of coupling SET with the AF approach that needs recharge (≈precipitation-ET)as one of the inputs, has not been researched yet. The CREMAP technique [16] based on WREVAP model [17] and a linear transformation (i.e., Min-Max) between regional level ET and surface temperature is also an option to explore.
6) In AF approach, recharge and depth to GWT are some of the most defining parameters [3] . On the other hand, using MODIS and PRSIM data, [18] shows that there exists a definite relationship between net recharge and depth to GWT. Therefore, integrating the AF approach with a relationship between net recharge and depth to GWT may potentially reduce the uncertainty associated with AF approach.
7) The major driver of water-level changes in many highly stressed aquifers (e.g., high plain aquifer in the central United States) is irrigation pumping that is a function of metrological conditions such as precipitation and ET [19] . In other words, with more pumping to meet irrigation demand, the water-level that is measured from the ground surface goes further down. On the other hand, with AF approach as explained through Equation (1-4), the decline on water-level (i.e., higher value for d) will decrease the value of AF. Consequently, the mass load of chemicals that reach the groundwater table declines. Therefore, should more pumping to meet irrigation demand be allowed? If not, what is the sustainable level? Considering the regulations for chemicals set by authorities (e.g., USEPA), the determination of sustainable level of water-level may be feasible with the AF approach. With this information, it may be appropriate to research on sustainable level of irrigation pumping and the impact of climatic and anthropogenic stresses.
8) Sensitivity analysis on model parameters are carried out to determine the sensitive ranking of parameters sorted by the amount of influence each has on model results [20] . Though, [3] has used Latin-Hypercube- One-factor-At-a-Time (LH-OAT) method to determine sensitivity of parameters, there is a need to conduct a comprehensive research on sensitivity analysis, as there are many sensitivity techniques that may result in different ranking. Though the actual ranking is not that important, the identification of input parameters that consistently appear near the top of the list, using different sensitivity techniques, is vital [20] . Furthermore, the distinction should be made between the parameter importance and parameter sensitivity.
9) The first level of uncertainty arises from the mathematical representation of the underlying physical processes that define the system of interest. Though [1] has outlined the incipient of AF approach through Equation (1-4), the need for further research that is bounded within the periphery of conceptual and detailed physical transformation is not precluded.
Acknowledgements
The authors would like to thank the Board of Regents, University of Nebraska-Lincoln, Lincoln, for providing the financial support to conduct this research. This research was conducted when author* was a researcher at University of Nebraska-Lincoln, Lincoln.
NOTES
![]()
*Corresponding author.