Numerical Study of the Higgs Mode in the Heisenberg Antiferromagnet on the Square Lattice ()
1. Introduction
The spontaneous symmetry breaking (SSB) of the continuous symmetry has been one of the most important concepts and phenomena of the modern physics [1] [2] . It is well known that the SSB induces the massless particle or the gapless mode, which is called the Nambu-Goldstone (NG) particle or mode [3] [4] . In the particle physics for the SSB mechanism we need another particle called the Higgs particle [5] . Recently the Higgs particle has been observed and its property has been confirmed to agree with the prediction of the standard model [6] [7] . However the quest on the Higgs particle has not finished, because many researchers consider that it is not a fundamental object of the underlying Hamiltonian [8] . Therefore we need deep understanding on the Higgs particle. The study of the Higgs mode in the other fields gives some keys for the next stage of its study.
In the condensed matter physics the Higgs mode has been extensively studied recently [9] . One can find many experimental reports on the existence of the Higgs mode. The authors of [10] have showed this mode in a two-dimensional neutral superfluid close to a quantum phase transition. The study of [11] about the material of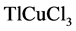 , has demonstrated a massive excitation corresponding to longitudinal fluctuations of the magnetic moment. For theoretical discussions on this material, see [12] . Also the experiment in [13] for the BCS superconductor
, has demonstrated a massive excitation corresponding to longitudinal fluctuations of the magnetic moment. For theoretical discussions on this material, see [12] . Also the experiment in [13] for the BCS superconductor 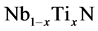 film has confirmed the appearance of the collective mode of the order parameter. One should note the experimental evidence for the observation of the superconducting Higgs mode in the charge density wave superconductor
film has confirmed the appearance of the collective mode of the order parameter. One should note the experimental evidence for the observation of the superconducting Higgs mode in the charge density wave superconductor  [14] .
[14] .
On the other hand theoretical study has been active, especially using the sigma model and other effective models. Its purpose is to find experimental possibilities of observing the Higgs mode [15] - [17] . Another is to understand the role of the Higgs mode near the critical point of the quantum phase transition [18] - [20] .
In this work we would like to study the Higgs mode in the spin-1/2 Heisenberg antiferromagnet on the square lattice [21] . This system has been studied extensively by the spin wave theory [22] as well as by numerical methods such as the quantum Monte Carlo method [23] - [25] and the exact diagonalisation [26] . The spin wave theory is quite successful in describing experimental results on this system. Note that this theory contains the NG modes, but not the Higgs mode. This success of the theory is due to the experimental difficulty of observing the Higgs mode [9] . As a result there are few theoretical works about the Higgs mode in the antiferromagnet.
The first motivation of our study is to find directly the Higgs mode in the quantum antiferromagnet. In this system the Hamiltonian is clearly defined and we have many materials that realize it. Therefore the numerical evidence for the Higgs mode should stimulate researchers to study experimentally as well as theoretically for this new degree of freedom in the condensed matter physics. Another motivation is to investigate how the Higgs mode is induced from the fundamental Hamiltonian. In the particle physics the Higgs particle is the object to constitute the Hamiltonian. By contrast, in the condensed matter physics the Higgs mode is not an object of the Hamiltonian, but the collective mode induced from it. Therefore we should be able to calculate the gap energy and other properties of the Higgs mode without any assumption. For this purpose the Hamiltonian of the Heisenberg antiferromagnet on the two-dimensional lattice is the most suitable because one can investigate it by various methods.
In our study on the Heisenberg antiferromagnet, the most important purpose is to find evidences for the Higgs mode on the finite lattice by the reliable method of the numerical calculations at zero temperature. Also we would like to clarify differences between the Higgs modes in the SU(2) symmetry and those in the U(1) symmetry through the study of the XXZ model [27] .
Since the Higgs mode is an excited state, we calculate the dynamical spin correlation. Here we employ the finite temperature Lanczos method [28] , which is the reliable diagonalisation approach.
In the next section after a brief description of the Higgs mode, we discuss procedures of finding evidences for it in our calculation. Here we emphasize that the Higgs mode is the excited mode and it couples with a pair of the NG-modes. Therefore the Higgs mode should be a resonance in the dynamical correlation of two spin operators. On the infinitely large lattice we can easily judge signals for the resonance. On the finite lattice, however, the numerical study for the resonance is a non-trivial task, because we calculate not continuous, but discrete energy eigen values. By taking this discreteness into account, we suggest four procedures to find the evidences. Numerical results are presented in Section 3. This section is divided to four subsections. In each subsection, we show the evidence for Higgs mode by using each suggested procedure. The final section is devoted to a summary and discussion for future researches.
2. Higgs Mode
The spin-1/2 Heisenberg antiferromagnet on the square lattice is given by
 (1)
(1)
Here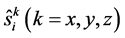 , is a spin operator on a site i and the sum runs over pairs of the neighbor sites on the square lattice.
, is a spin operator on a site i and the sum runs over pairs of the neighbor sites on the square lattice. 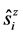 is a diagonal matrix, i.e. each state is represented by
is a diagonal matrix, i.e. each state is represented by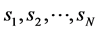 , where
, where  or
or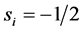 . N is a total number of sites. Since we make an exact diagonalisation by this representation, we can
. N is a total number of sites. Since we make an exact diagonalisation by this representation, we can
obtain eigen values of the  for a fixed value of a total
for a fixed value of a total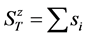 , where
, where 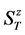 is an integer if N is an even
is an integer if N is an even
number. For each 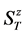 the lowest energy state is denoted by
the lowest energy state is denoted by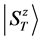 . Note that
. Note that , be-
, be-
cause the symmetry is not broken on a finite lattice system. In our representation the evidence of the SSB is given by the non-zero value of ![]() for a finite value of
for a finite value of![]() , where
, where ![]() is introduced by
is introduced by
![]() (2)
(2)
Here we denote a location by ![]() and
and![]() .
.
From the field theory on the SSB [2] [29] , for the ground state ![]() we have
we have
![]() (3)
(3)
Here ![]() is the charge,
is the charge, ![]() is the 0-th component of the current of the continuous symmetry
is the 0-th component of the current of the continuous symmetry
and ![]() is the field operator. From the discussion in [2] on (3) we know that there exists a field operator of the NG boson
is the field operator. From the discussion in [2] on (3) we know that there exists a field operator of the NG boson![]() , which appears in
, which appears in ![]() and
and![]() . If we neglect the higher order products of field operators, we have
. If we neglect the higher order products of field operators, we have
![]() (4)
(4)
![]() (5)
(5)
Here f is the decay constant and Z is the renormalization factor. If we apply the above discussion to the Heisenberg antiferromagnet on the square lattice, we have the following correspondence, as discussed in [29] .
![]()
![]()
![]()
Using the annihilation operator ![]() and the creation operator
and the creation operator ![]() for the NG mode of the wave vector
for the NG mode of the wave vector![]() , we obtain the correspondences,
, we obtain the correspondences,
![]() (6)
(6)
![]() (7)
(7)
Here ![]() and
and ![]() is the energy of the NG mode with the wave vector
is the energy of the NG mode with the wave vector![]() . For another NG mode, we use
. For another NG mode, we use ![]() as another current and use
as another current and use ![]() as the field operator. By the annihilation operator
as the field operator. By the annihilation operator ![]() and
and
the creation operator ![]() for another NG mode of the wave vector
for another NG mode of the wave vector![]() , we have the followings,
, we have the followings,
![]() (8)
(8)
![]() (9)
(9)
In the sigma model of the SSB, we have an interaction between the two NG modes and the Higgs mode. In order to obtain a state of the two NG modes, we apply two spin operators of ![]() to the lowest energy state
to the lowest energy state![]() . Therefore this application leads us to calculate the dynamical correlation [30] of the two spin operators at zero temperature in order to find the signal for the Higgs mode,
. Therefore this application leads us to calculate the dynamical correlation [30] of the two spin operators at zero temperature in order to find the signal for the Higgs mode,
![]() (10)
(10)
Here![]() ,
, ![]() is the energy eigen value of the state
is the energy eigen value of the state![]() ,
, ![]()
and![]() . Since the energy eigen value is discrete on the finite lattice, the delta-function is not well defined. For the definition of the delta-function on this lattice, we use a following function,
. Since the energy eigen value is discrete on the finite lattice, the delta-function is not well defined. For the definition of the delta-function on this lattice, we use a following function,
![]()
with the infinitely small![]() . Therefore we have a definition for the dynamical correlation on the finite size lattice
. Therefore we have a definition for the dynamical correlation on the finite size lattice
![]() (11)
(11)
We make ![]() to be zero after we take the large size limit. Let us consider a simple case of
to be zero after we take the large size limit. Let us consider a simple case of![]() . In this case we can use a simpler notation for the dynamical correlation,
. In this case we can use a simpler notation for the dynamical correlation,
![]() (12)
(12)
If only one resonance state exists as the Higgs mode in the large size limit, we have
![]() (13)
(13)
Here![]() , which does not depend on the wave vector
, which does not depend on the wave vector![]() , is the energy of the Higgs mode, and
, is the energy of the Higgs mode, and ![]() is the width of the resonance. On a finite lattice, however, the Hamiltonian has the discrete eigen values only. For a finite lattice size N, we have
is the width of the resonance. On a finite lattice, however, the Hamiltonian has the discrete eigen values only. For a finite lattice size N, we have
![]() (14)
(14)
Here we assume that![]() . If the limit in (13) exists,
. If the limit in (13) exists,
![]() will decrease with the larger N. Based on these considerations
will decrease with the larger N. Based on these considerations
about the Higgs mode on the finite lattice, we propose following four procedures to obtain numerical evidences on the existence of the Higgs mode.
(A) Since we generate the state with the pair of the NG modes from the ground state, which is ![]() on the finite lattice, we should see peaks in the correlation
on the finite lattice, we should see peaks in the correlation![]() . When
. When ![]() is sufficiently small, we can observe a peak which corresponds with each eigen value. If there are several peaks of
is sufficiently small, we can observe a peak which corresponds with each eigen value. If there are several peaks of![]() , in a narrow region of
, in a narrow region of![]() , an observation of these peaks is the basic evidence for the Higgs mode. In following three procedures, we make
, an observation of these peaks is the basic evidence for the Higgs mode. In following three procedures, we make ![]() a moderate value in order to examine clusters that are made by several eigen states.
a moderate value in order to examine clusters that are made by several eigen states.
(B) On a lattice of the finite size N we have the lowest energy state ![]() for each value of
for each value of![]() . In the SSB its energy
. In the SSB its energy ![]() agrees with
agrees with ![]() for the fixed value of
for the fixed value of![]() , when N becomes large, and we could not distinguish between states for
, when N becomes large, and we could not distinguish between states for ![]() on the infinitely large lattice. In addition we suppose that a physical quantity depends on
on the infinitely large lattice. In addition we suppose that a physical quantity depends on ![]() for the finite N, and the dependence can be expressed by a smooth function of
for the finite N, and the dependence can be expressed by a smooth function of![]() . For an example, the energy
. For an example, the energy ![]() is given by
is given by
![]()
Therefore the Higgs mode must exist on each![]() , and properties of the Higgs mode should be smooth functions of
, and properties of the Higgs mode should be smooth functions of![]() . If we observe this existence and these functions in our calculation, this observation is an evidence for the Higgs mode.
. If we observe this existence and these functions in our calculation, this observation is an evidence for the Higgs mode.
(C) On the square lattice, there is the NG mode at ![]() near
near ![]() [29] . Therefore we will find peaks in
[29] . Therefore we will find peaks in
![]() as well as peaks in
as well as peaks in ![]() when the wave vector
when the wave vector ![]() is near (0,0). If the shape
is near (0,0). If the shape
of the peak in ![]() is the same as that in
is the same as that in![]() , this observation is also an evidence for the Higgs mode.
, this observation is also an evidence for the Higgs mode.
(D) We will consider the XXZ model [27] , which has the U(1) symmetry only,
![]() (15)
(15)
where![]() . In this Hamiltonian the conserved current is only
. In this Hamiltonian the conserved current is only![]() . From the discussion on the correspondence between the current and the field operator of the NG boson, we should find the NG mode at k near (0,0), whereas the excitation at k near T cannot be the NG mode. As a result the peak in
. From the discussion on the correspondence between the current and the field operator of the NG boson, we should find the NG mode at k near (0,0), whereas the excitation at k near T cannot be the NG mode. As a result the peak in ![]() is not the Higgs mode A numerical evidence for this argument is a clear difference between the peaks of
is not the Higgs mode A numerical evidence for this argument is a clear difference between the peaks of ![]() in the Heisenberg antiferromagnet and those in the XXZ model.
in the Heisenberg antiferromagnet and those in the XXZ model.
In the next section we will show the above four evidences through numerical calculations of the dynamical correlation.
3. Numerical Results
In this section we present numerical results of our calculations about the Higgs mode in the Heisenberg antiferromagnet on the finite square lattice. Before presenting results shown in subsections, we describe three steps in calculations of![]() . The first step is to obtain the eigen state
. The first step is to obtain the eigen state ![]() with the lowest energy eigen value for each
with the lowest energy eigen value for each ![]() by the exact diagonalisation [26] . As the second step, we operate
by the exact diagonalisation [26] . As the second step, we operate ![]() to
to ![]() in order to make the state that includes the two NG modes of the wave vectors
in order to make the state that includes the two NG modes of the wave vectors ![]() and
and![]() . Since the state
. Since the state ![]() contains the contribution of
contains the contribution of![]() , we reduce its component from
, we reduce its component from![]() . Then we obtain the irreducible state,
. Then we obtain the irreducible state,
![]() (16)
(16)
Since the magnitude of the ![]() strongly depends on the lattice size and the wave vector, we will normalize the correlation in order to make a clear comparison among them for the various lattices and the various wave vectors. Therefore we examine the correlation,
strongly depends on the lattice size and the wave vector, we will normalize the correlation in order to make a clear comparison among them for the various lattices and the various wave vectors. Therefore we examine the correlation,
![]() (17)
(17)
where C is determined for the correlation to satisfy a following normalization,
![]() (18)
(18)
The third step of the calculation is to apply the finite temperature Lanczos method [28] [31] [32] by adopting ![]() as the initial state. Then following the usual Lanczos method, we generate the Lanczos states. The number of these states is fixed to 50, because we see no change in the results when this number is larger than 50. By these Lanczos states we diagonalise the Hamiltonian so that we obtain
as the initial state. Then following the usual Lanczos method, we generate the Lanczos states. The number of these states is fixed to 50, because we see no change in the results when this number is larger than 50. By these Lanczos states we diagonalise the Hamiltonian so that we obtain ![]() for any value of
for any value of![]() .
.
3.1. Results of the Dynamical Correlation
In this subsection we examine several peaks of the dynamical correlation in the narrow energy region in order to obtain the evidence by the first procedure (A) discussed in the Section 2. First we show results of the dynamical correlation ![]() for
for ![]() on the lattices of N = 20, 26, 32 and 36. The edge vector
on the lattices of N = 20, 26, 32 and 36. The edge vector![]() are (4,2), (5,1), (4,4) and (6,0) for N = 20, 26, 32 and 36, respectively. Here we impose the
are (4,2), (5,1), (4,4) and (6,0) for N = 20, 26, 32 and 36, respectively. Here we impose the ![]() rotational symmetry to the Hamiltonian. Therefore another edge vector
rotational symmetry to the Hamiltonian. Therefore another edge vector ![]() is given by
is given by![]() . Note that these edge vectors are defined uniquely for a given lattice size N except for accidental cases. Here
. Note that these edge vectors are defined uniquely for a given lattice size N except for accidental cases. Here![]() is the non-zero wave vector of the lowest magnitude on the each lattice. They are
is the non-zero wave vector of the lowest magnitude on the each lattice. They are![]() ,
, ![]() ,
, ![]() and
and ![]() for N = 20, 26, 32 and 36, respectively.
for N = 20, 26, 32 and 36, respectively.
Figure 1 shows the dynamical correlation ![]() versus
versus ![]() with the
with the![]() . Here
. Here ![]() is fixed
is fixed
to be sufficiently small in order that each peak corresponds to a single energy eigen state. By the procedure (A) of finding several peaks in the narrow energy region, we can obtain the first evidence for the Higgs mode.
We suppose that the Higgs mode appears as a resonance on the infinitely large lattice. On the finite lattice,
this resonance consists of the several energy eigen states. We would like to investigate the resonance which survives in the large N limit. For this purpose we make several peaks in Figure 1 to merge to one broad peak by using the larger![]() . Therefore this
. Therefore this ![]() must be larger than the energy difference between the peaks which form the resonance. On the other hand
must be larger than the energy difference between the peaks which form the resonance. On the other hand ![]() has to be smaller than the width of the resonance because, if we use the large
has to be smaller than the width of the resonance because, if we use the large![]() , the observed width becomes
, the observed width becomes ![]() and irrelevant to the width of the Higgs mode.
and irrelevant to the width of the Higgs mode.
By taking both conditions into account, we determine![]() . In following calculations we use this value. In Figure 2 of
. In following calculations we use this value. In Figure 2 of![]() , whose
, whose ![]() and the wave vector are the same as those in Figure 1 except for the value of
and the wave vector are the same as those in Figure 1 except for the value of![]() , we find the broad peaks. We can see that the cluster of peaks in Figure 1 merges to the single broad peak, which can be understood as the resonance. Such broad peak is found on all lattices. Although the energy at which we see the broad peak depends on the lattice size, this dependence is small.
, we find the broad peaks. We can see that the cluster of peaks in Figure 1 merges to the single broad peak, which can be understood as the resonance. Such broad peak is found on all lattices. Although the energy at which we see the broad peak depends on the lattice size, this dependence is small.
Here we make a comment on the sharp peak whose energy![]() , which is isolated from the broad peak. As seen in Figure 1, this peak is given by a single energy eigen value. Therefore we conclude that this peak is irrelevant to the resonance. This conclusion is supported by vanishing of this peak in
, which is isolated from the broad peak. As seen in Figure 1, this peak is given by a single energy eigen value. Therefore we conclude that this peak is irrelevant to the resonance. This conclusion is supported by vanishing of this peak in![]() , which will be shown in the next subsection.
, which will be shown in the next subsection.
3.2. Results for Total Spin S > 0
As discussed in the previous section, if the broad peaks found in Figure 2 are relevant to the Higgs mode, one should see similar peaks in the dynamical correlation of ![]() with other values of
with other values of![]() . Figure 3 gives us the correlation on the N = 36 lattice with
. Figure 3 gives us the correlation on the N = 36 lattice with![]() . The clear broad peaks are found in
. The clear broad peaks are found in ![]() for any
for any![]() . Here note that the
. Here note that the ![]() location, the height and the broadness of the peak change smoothly when
location, the height and the broadness of the peak change smoothly when ![]() increases.
increases.
In order to make quantitative discussion, we introduce definitions for the location of the peak and its broadness. First we find the ![]() where
where ![]() is maximal. Next we determine two values of
is maximal. Next we determine two values of![]() , at which
, at which
the value of ![]() is half of
is half of![]() . These two values are denoted as
. These two values are denoted as ![]() and
and ![]()
![]() . Here the central energy
. Here the central energy ![]() of a peak and the width
of a peak and the width ![]() are defined by
are defined by
![]() (19)
(19)
![]() (20)
(20)
For a concrete example, see Figure 4. Note that ![]() agrees with the resonance energy and
agrees with the resonance energy and ![]() agrees with its width, if
agrees with its width, if ![]() is a simple form of the Breit-Wigner resonance.
is a simple form of the Breit-Wigner resonance.
In Figure 5 we plot ![]() and
and ![]() for
for ![]() on N = 26, 32 and 36 lattices. We find that
on N = 26, 32 and 36 lattices. We find that ![]() depends on
depends on![]() , i.e.
, i.e. ![]() decreases with larger
decreases with larger![]() . It seems that
. It seems that ![]() is the linear function of
is the linear function of![]() . If we make the least square fit on each lattice, we obtain the errors of the fit, which are 0.058, 0.062 and 0.064 for N = 26, 32 and 36, respectively. These errors show that the linear function is acceptable for us. Also as dependences on the lattice size N,
. If we make the least square fit on each lattice, we obtain the errors of the fit, which are 0.058, 0.062 and 0.064 for N = 26, 32 and 36, respectively. These errors show that the linear function is acceptable for us. Also as dependences on the lattice size N, ![]() decreases weakly with larger N.
decreases weakly with larger N.
Next we will discuss the width ![]() of the broad peak.
of the broad peak. ![]() is smaller with larger
is smaller with larger![]() , and approaches to
, and approaches to![]() . If
. If ![]() agrees with
agrees with![]() , we understand that the peak is formed by a single eigen state. Also from this figure we observe that the width depend weakly on
, we understand that the peak is formed by a single eigen state. Also from this figure we observe that the width depend weakly on![]() . This dependence shows that we see the same resonance. By making the least square fit for
. This dependence shows that we see the same resonance. By making the least square fit for![]() , we plot the fitted lines in the figure. The errors of the fit are 0.064, 0.054 and 0.087 for N = 26, 32 and 36, respectively. These errors are worse than those of
, we plot the fitted lines in the figure. The errors of the fit are 0.064, 0.054 and 0.087 for N = 26, 32 and 36, respectively. These errors are worse than those of![]() .
.
Summarizing this subsection we conclude that the observation in the state for ![]() is the second evidence for the Higgs mode, as discussed in the Section 2.
is the second evidence for the Higgs mode, as discussed in the Section 2.
3.3. Two Kinds of the NG Modes
The SSB of the SU(2) symmetry of the Heisenberg antiferromagnet on the square lattice implies two kinds of the NG modes, as discussed in the previous section. One is the excited state of the small wave vector ![]() in
in![]() . Another is the excited state of the wave vector
. Another is the excited state of the wave vector ![]() in
in![]() . From the discussion by the sigma model for the SSB, we have one Higgs mode which has the same interaction with any kind of the NG modes. Therefore in the dynamical correlation
. From the discussion by the sigma model for the SSB, we have one Higgs mode which has the same interaction with any kind of the NG modes. Therefore in the dynamical correlation ![]() we should find the same resonance peak as that in
we should find the same resonance peak as that in ![]() for the small wave vector
for the small wave vector![]() . Since we calculate the correlation on the small lattice, the magnitude of the wave vector in our study is not so small. From the previous study [21] we can assume that the excited states with
. Since we calculate the correlation on the small lattice, the magnitude of the wave vector in our study is not so small. From the previous study [21] we can assume that the excited states with ![]() are candidates for the NG modes. On the N = 36 lattice, which is the maximal lattice in our calculation, the wave vector
are candidates for the NG modes. On the N = 36 lattice, which is the maximal lattice in our calculation, the wave vector ![]() has the magnitude of 1.047, and the wave vector
has the magnitude of 1.047, and the wave vector![]() has the magnitude of 1.481. Therefore on the N = 36 lattice we calculate the dynamical correlation on the excited states of the wave vectors
has the magnitude of 1.481. Therefore on the N = 36 lattice we calculate the dynamical correlation on the excited states of the wave vectors ![]() and
and![]() , as well as
, as well as ![]() and
and![]() . In addition this is calculated for the wave vectors of
. In addition this is calculated for the wave vectors of ![]() and
and ![]() on the N = 32 lattice. Here note that the wave vector
on the N = 32 lattice. Here note that the wave vector ![]() has the magnitude of 1.111.
has the magnitude of 1.111.
In Figure 6 we show ![]() with the above wave vectors. The first noticeable observation is the excellent agreement between peaks of the wave vector
with the above wave vectors. The first noticeable observation is the excellent agreement between peaks of the wave vector ![]() and
and![]() . On the peaks with the smallest wave vector
. On the peaks with the smallest wave vector ![]() and
and![]() , the agreement is not perfect due to the dip in the peak with
, the agreement is not perfect due to the dip in the peak with![]() . As we will discuss in the summary, we suppose that the dip is artificial by the lattice symmetry. In order to confirm that this disagreement is accidental, we calculate
. As we will discuss in the summary, we suppose that the dip is artificial by the lattice symmetry. In order to confirm that this disagreement is accidental, we calculate ![]() with
with ![]() and the wave vector
and the wave vector ![]() and
and![]() . These results are included in Figure 6, where we find the agreement between
. These results are included in Figure 6, where we find the agreement between
these peaks. Also the result on the N = 32 lattice shows the similar agreement between peaks of the correlation with the wave vector ![]() and
and![]() . These agreements can be explained by a fact that the Higgs mode couples to two kinds of the NG modes and it couples at the same strength to them. Therefore this observation is the strong evidence for the Higgs mode in the SU(2) symmetry.
. These agreements can be explained by a fact that the Higgs mode couples to two kinds of the NG modes and it couples at the same strength to them. Therefore this observation is the strong evidence for the Higgs mode in the SU(2) symmetry.
3.4. Results about the XXZ Model
In this subsection we will carefully examine the broad peaks in ![]() and
and ![]() of the XXZ model.
of the XXZ model.
As discussed in the previous subsection, the agreement between the peaks in these correlations reflects the symmetry of SU(2). If the symmetry of the model is U(1), we should not expect agreements between these peaks. Therefore we would like to study the correlation in the XXZ model which has only the U(1) symmetry. The Hamiltonian of the XXZ model is given by (15) in the Section 2. Since in this model the conserved charge is![]() , the 0-th component of conserved current corresponds with
, the 0-th component of conserved current corresponds with![]() . By this consideration, the NG mode appears in
. By this consideration, the NG mode appears in ![]() with the small wave vector
with the small wave vector ![]() and we can expect the broad peak by the Higgs mode in
and we can expect the broad peak by the Higgs mode in
![]() . On the contrary the peak in
. On the contrary the peak in ![]() is irrelevant to the Higgs mode.
is irrelevant to the Higgs mode.
In Figure 7 we show ![]() and
and ![]() about models of l = 0.1, 0.2, 0.3, 0.5, 0.8 and 1 (Heisenberg model). Here the lattice size N is 36 and the wave vector
about models of l = 0.1, 0.2, 0.3, 0.5, 0.8 and 1 (Heisenberg model). Here the lattice size N is 36 and the wave vector ![]() is
is![]() . As is expected, these peaks of
. As is expected, these peaks of ![]() and
and ![]() begin to separate from each other when l deceases from 1. The central energy
begin to separate from each other when l deceases from 1. The central energy ![]() of the broad peaks for the wave vector
of the broad peaks for the wave vector ![]() decreases when l deceases. Also the width
decreases when l deceases. Also the width ![]() becomes smaller. On the other hand the central energy
becomes smaller. On the other hand the central energy ![]() for the wave vector
for the wave vector ![]() increases and the width
increases and the width ![]() does not change clearly. We show the central energy of the broad peaks on the lattices of N = 26, 32 and 36 in Figure 8. From results in Figure 7 and Figure 8, we obtain the fourth evidence for the Higgs mode by the separated peaks in
does not change clearly. We show the central energy of the broad peaks on the lattices of N = 26, 32 and 36 in Figure 8. From results in Figure 7 and Figure 8, we obtain the fourth evidence for the Higgs mode by the separated peaks in ![]() and
and ![]() in the XXZ model.
in the XXZ model.
4. Summary and Discussion
In this work we have presented the numerical evidences for the Higgs mode of the spin-1/2 Heisenberg antiferromagnet on the square lattice, using the exact diagonalisation method and the finite temperature Lanczos method. Since the Higgs mode is the resonance which couples with the two Nambu-Goldstone (NG) modes, we calculate the dynamical correlation of the two spin operators with various wave vectors at zero temperature. For the dynamical correlation we have to calculate the inverse of the Hamiltonian operator. Since our calculations are carried out on the finite lattice, we need the smearing parameter ![]() to avoid the singular behavior of the inverse operator.
to avoid the singular behavior of the inverse operator.
In this work we suggest four procedures (A)-(D) to find the Higgs mode in the calculation of the dynamical correlation. Using the first procedure (A) about peaks in the correlation with the small value of![]() , we observe many peaks in the narrow energy region, which gives us the first evidence for the Higgs mode. By calculations with the moderate value of
, we observe many peaks in the narrow energy region, which gives us the first evidence for the Higgs mode. By calculations with the moderate value of![]() , we have found broad peaks on the lattices of various sizes. The second procedure (B) is suggested by a fact that the property of a state with any value of
, we have found broad peaks on the lattices of various sizes. The second procedure (B) is suggested by a fact that the property of a state with any value of ![]() should agree with that of the state
should agree with that of the state![]() , because the spontaneous breaking of the continuous symmetry requires the degenerated states. Although this agreement is obtained on the infinitely large lattice, the property on a state with non-zero value of
, because the spontaneous breaking of the continuous symmetry requires the degenerated states. Although this agreement is obtained on the infinitely large lattice, the property on a state with non-zero value of ![]() on the finite lattice should be the smooth function of
on the finite lattice should be the smooth function of![]() . The study on the lattices of N = 26, 32 and 36 has shown that the central energy of the broad peaks is the linear function of
. The study on the lattices of N = 26, 32 and 36 has shown that the central energy of the broad peaks is the linear function of![]() . This is the second evidence for the Higgs mode. By noticing that the SU(2) symmetry is broken by the O(3) scalar model, i.e. we have only one Higgs mode as well as two kinds of the NG modes, we suggest the third procedure (C). The Hamiltonian has the SU(2) symmetry so that we have the NG mode of the wave vector
. This is the second evidence for the Higgs mode. By noticing that the SU(2) symmetry is broken by the O(3) scalar model, i.e. we have only one Higgs mode as well as two kinds of the NG modes, we suggest the third procedure (C). The Hamiltonian has the SU(2) symmetry so that we have the NG mode of the wave vector ![]() as well as those of
as well as those of ![]() for the small
for the small ![]() and
and![]() . Since these NG modes interact with the same Higgs mode, we should find the same broad peaks in the dynamical correlation with
. Since these NG modes interact with the same Higgs mode, we should find the same broad peaks in the dynamical correlation with ![]() as those with
as those with![]() . The calculations of
. The calculations of ![]() with
with ![]() and
and ![]() with
with ![]() on the lattice of N = 36 have given us the strong support for the same broad peaks. Also we find the same peaks in the calculations of
on the lattice of N = 36 have given us the strong support for the same broad peaks. Also we find the same peaks in the calculations of ![]() with
with ![]() on the lattice of N = 32. These results give us the third evidence for the Higgs mode. By the observation of these same broad peaks, we suggest the fourth procedure (D), which makes a comparison between the Higgs modes of the SU(2) and the U(1) symmetry. For this purpose we study XXZ model which has only U(1) symmetry. In this model the excited mode of the wave vector
on the lattice of N = 32. These results give us the third evidence for the Higgs mode. By the observation of these same broad peaks, we suggest the fourth procedure (D), which makes a comparison between the Higgs modes of the SU(2) and the U(1) symmetry. For this purpose we study XXZ model which has only U(1) symmetry. In this model the excited mode of the wave vector ![]() for small
for small ![]() and
and ![]() is the NG mode, while the mode of
is the NG mode, while the mode of ![]() is not. Therefore the excited mode of the wave vector
is not. Therefore the excited mode of the wave vector ![]() does not interact with the Higgs mode. Our study about the various XXZ models has showed that the broad peak in the correlation with
does not interact with the Higgs mode. Our study about the various XXZ models has showed that the broad peak in the correlation with ![]() is separated from the peaks with
is separated from the peaks with![]() . This observation has given us the fourth evidence. By these evidences we can confirm the existence of the Higgs mode in the Heisenberg antiferromagnet on the square lattice.
. This observation has given us the fourth evidence. By these evidences we can confirm the existence of the Higgs mode in the Heisenberg antiferromagnet on the square lattice.
Now we comment on the dip that is seen in the broad peak of the correlation of N = 36, ![]() and
and![]() . The similar dip is found in the peak of N = 26,
. The similar dip is found in the peak of N = 26, ![]() and
and![]() . We suppose that these dips are accidental because we do not see the dip for
. We suppose that these dips are accidental because we do not see the dip for![]() . Also on the small lattices we do not see the dip, as shown in Figure 9. This figure gives us results of N = 18, 20, 25a and 25b for
. Also on the small lattices we do not see the dip, as shown in Figure 9. This figure gives us results of N = 18, 20, 25a and 25b for![]() , where the edge vectors are (3,3), (4,2), (4,3) and (5,0). Here we assume the symmetry of
, where the edge vectors are (3,3), (4,2), (4,3) and (5,0). Here we assume the symmetry of ![]() rotation. Also we can see the dependence of peaks on the edge vector, if we make a comparison between results of the edge vector (4,3) for 25a and that of the edge vector (5,0) for 25b.
rotation. Also we can see the dependence of peaks on the edge vector, if we make a comparison between results of the edge vector (4,3) for 25a and that of the edge vector (5,0) for 25b.
Since we have calculated the central energy ![]() of the broad peak on many lattices, we discuss
of the broad peak on many lattices, we discuss ![]() on the infinitely large lattice. When we assume that
on the infinitely large lattice. When we assume that
![]() (21)
(21)
we obtain ![]() for
for![]() , while we obtain
, while we obtain ![]() for
for ![]() Although the estimated error is not small, one should note that this is clearly non-zero, and they give the same value. Using the same analysis for the width, we obtain
Although the estimated error is not small, one should note that this is clearly non-zero, and they give the same value. Using the same analysis for the width, we obtain ![]() for
for ![]() and
and ![]() for
for![]() . The width for
. The width for ![]() does not agree with that for
does not agree with that for![]() , but it is clear that they are larger than
, but it is clear that they are larger than![]() . This implies that we obtain the finite width on the infinitely large lattice.
. This implies that we obtain the finite width on the infinitely large lattice.
Finally we would like to discuss about further study of the Higgs mode. If the broad peak is the resonance of the Higgs mode, we should find the same peak that has the same central energy ![]() and the same width
and the same width ![]() for any pair of the NG modes of the wave vectors
for any pair of the NG modes of the wave vectors ![]() and
and![]() . In the present work we employ the exact diagonalisation approach, by which the size of the lattice is severely limited. As a result the wave vector is not small enough even for the N = 36 lattice, and we cannot find the same peak in the dynamical correlation with more than two kinds of the wave vectors. Therefore it is quite important to find the same peak for various wave vectors on larger lattices.
. In the present work we employ the exact diagonalisation approach, by which the size of the lattice is severely limited. As a result the wave vector is not small enough even for the N = 36 lattice, and we cannot find the same peak in the dynamical correlation with more than two kinds of the wave vectors. Therefore it is quite important to find the same peak for various wave vectors on larger lattices.
![]()
Figure 9. The dynamical correlation of two spin operators ![]() on the small lattices of N = 18, 20, 25a and 25b. The magnitude of the wave vector
on the small lattices of N = 18, 20, 25a and 25b. The magnitude of the wave vector ![]() is the smallest for each lattice. The edge vector for N = 25a is (4,3), while it for N = 25b is (5,0). The lattice size is 25 for both edge vectors. The wave vectors for N = 18, 20, 25a and 25b are
is the smallest for each lattice. The edge vector for N = 25a is (4,3), while it for N = 25b is (5,0). The lattice size is 25 for both edge vectors. The wave vectors for N = 18, 20, 25a and 25b are![]() ,
, ![]() ,
, ![]() and
and![]() , respectively.
, respectively.
In this work our calculations are made at the zero temperature. The extensive study at the finite temperature is an important subject because the experiments are performed at the finite temperature. Also the Higgs mode in two dimensional systems near a quantum critical point has been a subject of debate [15] - [20] . Our approach to the Higgs mode is useful to study models with the quantum phase transition.
Acknowledgements
M. T. thanks Dr. Yasuko Munehisa for every encouragement on his study.