A Solution of the Burger’s Equation Arising in the Longitudinal Dispersion Phenomenon in Fluid Flow through Porous Media by Mixture of New Integral Transform and Homotopy Perturbation Method ()
1. Introduction
The present paper discusses the solution of longitudinal dispersion phenomenon arising in the miscible fluid flow through homogenous porous media. The problem of solute dispersion during underground water movement has attracted interest from the early days of this century [1] , but it has been only since 1905 in general topic of hydrodynamic dispersion or miscible displacement becomes one of the more systematic studies. The dispersion phenomenon has been receiving good attention from hydrologist, agriculture, environmental, mathematicians, chemical engineering and soil scientists. The specific problem of fluid mixing in fixed bed reactors has been investigated by Bernard and Wilhelm [2] . Kovo [3] has worked with the parameter to be modeled in the longitudinal or axial dispersion coefficient in chemical reactors model.
The problem is to find the concentration as a function of time t and position x, as two miscible fluids flow through porous media on either sides of the mixed region, the single fluid equation describes the motion of the fluid. The problem becomes more complicated in one dimension with fluids of equal properties. Hence, the mixing takes place longitudinally as well as transversely at time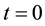 , a dot of fluid having
, a dot of fluid having 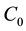 concentration is injected over the phase. It is shown in Figure 1. The dot moves in the direction of flow as well as perpendicular to the flow. Finally, it takes the shape of ellipse with a different concentration
concentration is injected over the phase. It is shown in Figure 1. The dot moves in the direction of flow as well as perpendicular to the flow. Finally, it takes the shape of ellipse with a different concentration .
.
Most of the works reveal common assumption of homogenous porous media with constant porosity, steady seepage flow velocity and constant dispersion coefficient. For such assumption, Ebach and White [4] have studied the longitudinal dispersion problem for an input concentration that varies periodically with time. Hunt [5] applied the perturbation method to longitudinal and lateral dispersion in no uniform seepage flow through heterogeneous aquifers. Patel and Mehta [6] applied Hope-Cole transformation to unsteady flow against dispersion of miscible fluid flow through porous media. Meher and Mehta [7] studied the Dispersion of Miscible fluid in semi infinite porous media with unsteady velocity distribution using Adomain decomposing method.
A new integral transform is derived from the classical Fourier integral. A new integral transform [8] was introduced by Artion Kashuri and Akli Fundo to facilitate the process of solving ordinary and partial differential equations in the time domain. Some integral transform methods such as Laplace, Fourier, Sumudu and Elzaki transforms methods, are used to solve general nonlinear non-homogenous partial differential equations with initial conditions and use fullness of these integral transform lies in their ability to transform differential equations into algebraic equations which allows simple and systematic solution procedures. Non-linear phenomena, that appear in many areas of scientific fields such as solid state physics, plasma physics, fluid mechanics, population models and chemical kinetics, can be modeled by nonlinear differential equations. The importance of obtaining
![]()
Figure 1. Longitudinal dispersion phenomenon.
the exact or approximate solutions of nonlinear partial differential equations in physics and mathematics is still a significant problem that needs new methods to discover exact or approximate solutions. Also a new integral transform and some of its fundamental properties are used to solve general nonlinear partial differential equation with appropriate initial conditions.
A new integral transform is defined for functions of exponential order. We consider functions in the set defined as
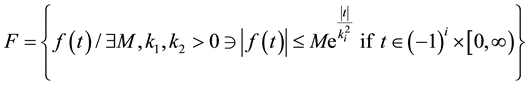 (1)
(1)
For a given function in the set F, the constant M must be finite number, 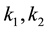 may be finite or infinite.
may be finite or infinite.
A new integral transform denoted by the operator  is defined by:
is defined by:
 (2)
(2)
In this paper, we have combined a new integral transform and homotopy perturbation method (HPM) to solve Burger’s equation arising in the dispersion phenomenon. The purpose of this study is to show the applicability and the efficiency of this mixture method.
2. Mathematical Formulation of the Problem
According to Darcy’s law, the equation of continuity for the mixture, in the case of compressible fluids is given by Bear [1] ,
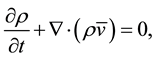 (3)
(3)
where 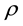 is the density for the mixture and
is the density for the mixture and 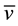 is the pore seepage velocity.
is the pore seepage velocity.
The equation of diffusion for a fluid flow through a homogeneous porous medium, without increasing or decreasing the dispersing material is given by,
 (4)
(4)
where C is the concentration of the fluids,  is the tensor coefficients of dispersion with nine components
is the tensor coefficients of dispersion with nine components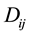 .
.
In a laminar flow through homogeneous porous medium at a constant temperature, 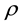 is constant.
is constant.
Then
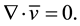 (5)
(5)
Therefore Equation (4) becomes,
![]() (6)
(6)
When the seepage velocity is the along x-axis, the nonzero components are ![]() (Coefficients of longitudinal dispersion, is a function of x along the x-axis) and other
(Coefficients of longitudinal dispersion, is a function of x along the x-axis) and other ![]() are zero [9] .
are zero [9] .
In this case, Equation (6) becomes
![]() (7)
(7)
where is the component of velocity along the ![]() -axis, which is time dependent as well as concentration along the
-axis, which is time dependent as well as concentration along the ![]() -axis in
-axis in ![]() direction and
direction and![]() , and it is cross-sectional flow velocity of porous medium. Therefore
, and it is cross-sectional flow velocity of porous medium. Therefore
![]() (8)
(8)
where ![]() and for
and for ![]() [10]
[10]
Hence Equation (7) becomes
![]() (9)
(9)
This is the non linear Burger’s equation for longitudinal dispersion of miscible fluid flow through porous media. The theory that follows is confined to dispersion in unidirectional seepage flow through semi-infinite homogeneous porous media. The seepage flow velocity is assumed unsteady. The dispersion systems to be considered are subject to an input concentration of contaminants![]() . The governing partial differential Equation (9) for longitudinal hydrodynamic dispersion with in a semi-infinite non-adsorbing porous medium in a unidirectional flow field in which
. The governing partial differential Equation (9) for longitudinal hydrodynamic dispersion with in a semi-infinite non-adsorbing porous medium in a unidirectional flow field in which ![]() is the longitudinal dispersion coefficient, C is the average cross-sectional concentration,
is the longitudinal dispersion coefficient, C is the average cross-sectional concentration, ![]() is the unsteady seepage velocity, x is a coordinate parallel to flow and t is time.
is the unsteady seepage velocity, x is a coordinate parallel to flow and t is time.
3. Solution of the Problem
In this section, the effectiveness and the usefulness of mixture of new integral transform and homotopy perturbation method is demonstrated by finding the solution of non-linear Burger’s equation for longitudinal dispersion arising in fluid flow through porous media.
The initial and boundary conditions for the Problem (9) are
![]() (10)
(10)
Since concentration is decreasing as x with distance x. Therefore for the sake of convenience ![]() is considered as negative exponential function [10] .
is considered as negative exponential function [10] .
By applying a new integral transform of Equation (9) subject to the boundary and initial conditions (12) we have
![]() (11)
(11)
The inverse new integral transform implies that,
![]() (12)
(12)
Now applying homotopy perturbation method in Equation (12), we get
![]() (13)
(13)
where,![]() .
.
![]()
Comparing the coefficients of the same power of ![]() and
and ![]() in Equation (13), we get
in Equation (13), we get
![]()
Thus the solution ![]() is given by
is given by
![]() (14)
(14)
The solution (14) represents the concentration of the longitudinal dispersion phenomenon for any value of ![]() and for any time t.
and for any time t.
4. Numerical and Graphical Representation
Expression (14) represents the solution of Burger’s equation arising in longitudinal dispersion phenomenon in fluid flow through porous media which is the concentration for any time t = 0.001, 0.002, 0.003, 0.004, 0.005, 0.006, 0.007, 0.008, 0.009 and 0.01 (Table 1). Figure 2 shows the concentration versus distance x when time t is fixed.
5. Conclusion
The main goal of this paper is to solve Burger’s equation arising in longitudinal dispersion phenomenon in fluid flow through porous media by the mixture of the new integral transform with the homotopy perturbation method. The analytical expressions obtained here are useful to the study of salinity intrusion in groundwater, helpful in making quantitative predictions on the possible contamination of groundwater supplies resulting from groundwater movement through buried wastes. Numerical and graphical representation of solution presents possible
![]()
Table 1. The value of concentration for different value of distance x and time t.
![]() (a)
(a)![]() (b)
(b)
Figure 2. (a) Concentration (C) versus distance (x); (b) Concentration (C) versus time (t).
concentration of a given dissolved substance in unsteady unidirectional seepage flows through semi-infinite, homogeneous, isotropic porous media subject to the source concentrations that vary negative exponentially with distance and slightly increases with time.