1. Introduction
In this paper, we define various characteristic classes on a super vector bundle over a superspace, so called super characteristic classes. We also propose the super Riemann-Roch formulas and the super Gauss-Bonnet formulas as its application. In contrast, it is justified the definition of the super characteristic classes by establishing those formulas. In [1] , we defined the super Chern classes with values in the super number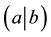 ,
, 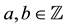 and we succeeded in applying the super ADHM construction of the super Yang-Mills instantons. But essentially the super Chern classes ought to take with values in an integer
and we succeeded in applying the super ADHM construction of the super Yang-Mills instantons. But essentially the super Chern classes ought to take with values in an integer . Meaning like it, we introduce the new definition of the super Chern classes with values in integer. In general, the characteristic classes consider that given the vector bundles it corresponds to some cohomology class of the base manifolds. Hence, we need the cohomology reflecting the properties of superspaces. Therefore, we will define the cohomology with respect to coefficient of the some finitely generated group, which is called the helicity group.
. Meaning like it, we introduce the new definition of the super Chern classes with values in integer. In general, the characteristic classes consider that given the vector bundles it corresponds to some cohomology class of the base manifolds. Hence, we need the cohomology reflecting the properties of superspaces. Therefore, we will define the cohomology with respect to coefficient of the some finitely generated group, which is called the helicity group.
This article is organized as follows. After a brief sketch on the definition and examples of superspaces and its cohomology in Section 2 ([1] -[6] ), main result in this paper is that we define the Chern class, Chern character, Todd class, Pontrjagin class, Eular class, 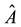 -genus and L-genus as in the case of super category in Section 3. In Section 4, as an application, we have the Riemann-Roch type formula of super structure sheaf on the complex supercurves of dimension
-genus and L-genus as in the case of super category in Section 3. In Section 4, as an application, we have the Riemann-Roch type formula of super structure sheaf on the complex supercurves of dimension  with genus g. Moreover, it generalizes the structure sheaf to any super line sheaves. In particular, in the case of dimension
with genus g. Moreover, it generalizes the structure sheaf to any super line sheaves. In particular, in the case of dimension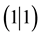 , with
, with 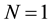 supersymmetric structure, we obtain the Atiyah-Singer index type formula for any super line bundles. In Section 5, we attempt to define the helicity group and cohomology with respect to coefficient of the helicity group. In Section 6, we give the Gauss-Bonnet type formula on the complex supercurves of dimension
supersymmetric structure, we obtain the Atiyah-Singer index type formula for any super line bundles. In Section 5, we attempt to define the helicity group and cohomology with respect to coefficient of the helicity group. In Section 6, we give the Gauss-Bonnet type formula on the complex supercurves of dimension  with genus g and the complex super projectve space of dimension
with genus g and the complex super projectve space of dimension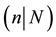 .
.
2. Supermanifolds
We will summarize the definitions here in order to establish terminology and notation ([1] -[6] ).
Definition 2.1 A superspace is defined to be a local ringed space 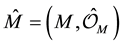 consisting a topological
consisting a topological
space M and a sheaf of 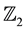 -graded supercommutative rings
-graded supercommutative rings 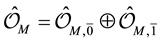 on it such that the stalk
on it such that the stalk 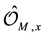 at any point
at any point 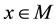 is a local ring.
is a local ring.
In particular case of a superspace, a supermanifold is defined by the following.
Definition 2.2 A supermanifold of dimension 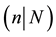 is a ringed space
is a ringed space 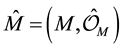 with the following properties:
with the following properties:
1) the structure sheaf ![]() is a sheaf of
is a sheaf of ![]() -graded supercommutative rings,
-graded supercommutative rings,
2) Let ![]() be the ideal sheaf of nilpotents in
be the ideal sheaf of nilpotents in![]() . Then
. Then ![]() is a classical manifold M of dimension n, so also called body.
is a classical manifold M of dimension n, so also called body.
3) Let ![]() be the locally free
be the locally free ![]() -module of rank
-module of rank![]() . Then
. Then ![]() is locally isomorphic to the exterior algebra
is locally isomorphic to the exterior algebra![]() .
.
A supermanifold is said to be split if the isomorphism 3) holds globally.
A local section ![]() can be expressed as follows:
can be expressed as follows:
![]() (1)
(1)
where![]() ,
, ![]() is a local coordinate function on
is a local coordinate function on ![]() and
and ![]() a local
a local
generator of![]() . We refer to
. We refer to ![]() as a local coordinate of a supermanifold
as a local coordinate of a supermanifold![]() .
.
Example 2.1 1) The typical example is the real (or complex) linear superspace ![]() (or
(or![]() ) which can be defined by
) which can be defined by
![]()
![]()
where ![]() (or
(or![]() ) is the sheaf of the ring of differential functions on
) is the sheaf of the ring of differential functions on ![]() (or
(or![]() ). It is easy to see that
). It is easy to see that
the ![]() is isomorphic to
is isomorphic to![]() .
.
2) A real super sphere of dimension ![]() is defined by
is defined by
![]()
where ![]() is the sheaf of the ring of differential functions on
is the sheaf of the ring of differential functions on![]() .
.
3) A complex super projective space of dimensin ![]() is defined by
is defined by
![]()
We denote by ![]() the structure sheaf
the structure sheaf ![]() of
of![]() . A super holomorphic function 1) on
. A super holomorphic function 1) on ![]() should be a function of total homogeneity 0 in
should be a function of total homogeneity 0 in ![]() even variables
even variables ![]() and N odd variables
and N odd variables![]() , that is
, that is ![]() has homogeneity
has homogeneity![]() . Let
. Let ![]() be the even line sheaf of degree d on
be the even line sheaf of degree d on ![]() and
and ![]() be the odd line sheaf of degree d on
be the odd line sheaf of degree d on![]() .
.
4) A quaternionic super projective space of dimension ![]() is defined by
is defined by
![]()
The above are examples of the supermanifolds in Definition 2.2.
5) We have a new example of superspace in Definition 2.1 as follows. The complex supercurves of dimension ![]() with genus g is defined by
with genus g is defined by
![]()
where ![]() is the canonical line bundle on the classical Riemann surfaces
is the canonical line bundle on the classical Riemann surfaces ![]() and
and![]() . In the case of
. In the case of![]() , it becomes the super Riemann surfaces with
, it becomes the super Riemann surfaces with ![]() SUSY structure (c.f. [7] , p.162). In the case of
SUSY structure (c.f. [7] , p.162). In the case of![]() , we do not kown whether or not there exists a SUSY structure.
, we do not kown whether or not there exists a SUSY structure.
We can construct the super Euler sequence as follows ([1] ).
![]()
Tensoring this with![]() , we have
, we have
![]()
Considering the super determinant ( so called Berezin bundle ) of the super Euler sequence, we obtain
![]()
Dualizing this, we can write
![]()
where ![]() calls the canonical super line bundle of
calls the canonical super line bundle of ![]() and
and ![]() is the parity change functor. The fol- lowing is given by Manin ([5] ).
is the parity change functor. The fol- lowing is given by Manin ([5] ).
Lemma 2.1
![]()
![]()
![]()
where ![]() and
and![]() .
.
The following is given by Penkov ([8] ).
Theorem 2.1 (Super Serre Duality) Let E be a complex super vector bundle over![]() . Suppose that
. Suppose that ![]() is the canonical super line bundle of
is the canonical super line bundle of![]() . Then we have the following.
. Then we have the following.
![]()
3. Super Characteristic Class
In this section, we will give a main result in this paper. Let ![]() denote the structure sheaf on
denote the structure sheaf on![]() . Then we have an exact sequence (cf. [2] , p.166 Lemma 2.1)
. Then we have an exact sequence (cf. [2] , p.166 Lemma 2.1)
![]()
where ![]() is the natural injection and exp is defined by
is the natural injection and exp is defined by
![]()
The ![]() implies
implies![]() ,
,![]() . Hence
. Hence![]() . This induces the exact sequence of cohomology groups:
. This induces the exact sequence of cohomology groups:
![]()
We can identify ![]() with the equivalence classes of
with the equivalence classes of ![]() or
or ![]() -super line bundles over
-super line bundles over![]() . Then we can define the super first Chern class of
. Then we can define the super first Chern class of ![]() -super line bundle L and
-super line bundle L and ![]() -super line bundle
-super line bundle ![]() by
by
![]()
Remark 3.1 Note that we can define![]() . We consider the line sheaf
. We consider the line sheaf ![]() over the complex super projective space
over the complex super projective space![]() . This line sheaf is decomposed into
. This line sheaf is decomposed into
![]()
The super first Chern calss and the classical first Chern class denote by ![]() and
and![]() , respectively. Then we have
, respectively. Then we have
![]()
![]()
Hence, we see that for the superline bundle L
![]()
We will propose the axiomatic definition of super Chern classes (cf. [1] [2] [9] -[15] ). We consider the category of complex ![]() -super vector bundles over an
-super vector bundles over an ![]() -superspace
-superspace![]() .
.
Axiom 1 For each complex super vector bundle E over ![]() and for each positive integer i, the i-th super Chern class
and for each positive integer i, the i-th super Chern class ![]() is given, and
is given, and![]() .
.
We set ![]() and call
and call ![]() the total super Chern class of E.
the total super Chern class of E.
Axiom 2 (Naturality)
Let E be a complex super vector bundle over a superspace ![]() and
and ![]() a morphism of superspaces. Then
a morphism of superspaces. Then
![]()
where ![]() is the pull-back bundle over
is the pull-back bundle over![]() .
.
Axiom 3 (Whitney sum formula)
Let ![]() be complex line bundles of rank
be complex line bundles of rank ![]() or
or ![]() and
and ![]() be their Whitney sum. Then
be their Whitney sum. Then
![]()
Axiom 4 (Normalization)
We put ![]() and
and![]() . Then it can be axiomatically as follows:
. Then it can be axiomatically as follows:
![]()
![]()
![]()
In order to explicitly define the super characteristic classes we need the splitting principle ([2] Proposition 3.7) as follows.
Proposition 3.1 (Bartocci, Bruzzo, Hernandez-Ruiperez) Let E be a complex ![]() -super vector bundle over an
-super vector bundle over an ![]() -supermanifold
-supermanifold![]() . Then there exists a supermanifold
. Then there exists a supermanifold ![]() and a proper fibration
and a proper fibration ![]() such that
such that
1) The homomorphism ![]() is injective.
is injective.
2) The pull-back bundle ![]() splits into a direct sum of even complex line bundles
splits into a direct sum of even complex line bundles ![]() of rank
of rank ![]() and odd complex line bundles
and odd complex line bundles ![]() of rank
of rank![]() :
:
![]()
![]()
We will explicitly give the super characteristic classes.
Definition 3.1 1) The total super Chern class ![]() is defined by
is defined by
![]()
2) The total super Chern character ![]() is defined by
is defined by
![]()
3) The super Todd class ![]() is defined by
is defined by
![]()
4) The super Eular class ![]() is defined by
is defined by
![]()
5) Let ![]() be a real vector bundle of rank
be a real vector bundle of rank![]() . The i-th super Pontrjagin class
. The i-th super Pontrjagin class ![]() and the total super Pontrjagin class are defined by
and the total super Pontrjagin class are defined by
![]()
![]()
6) The super ![]() -genus
-genus ![]() is defined by
is defined by
![]()
7) The super L-genus ![]() is defined by
is defined by
![]()
We can consider that it is justified these definitions by the following (cf. [13] [14] ).
Lemma 3.1 The first few terms of ![]() and
and ![]() are given by the following.
are given by the following.
![]()
![]()
![]()
Proof. Let E be a complex rank-![]() super vector bundle over a complex
super vector bundle over a complex ![]() -dimensional supermanifold
-dimensional supermanifold![]() . Then, total super Chern class is written by
. Then, total super Chern class is written by
![]()
Hence, we have
![]()
![]()
![]()
The total super Chern character is written by
![]()
Hence we have
![]() ,
,
![]() ,
,
![]() ,
,
![]() .
.
It is well-known thtat
![]()
![]()
Hence the total super Todd class is written by
![]()
Therefore we have
![]() ,
,
![]() ,
,
![]() ,
,
![]() .
.
Then, they satisfy that
![]()
![]()
![]()
W
Lemma 3.2 The first few terms of![]() ,
, ![]() and
and ![]() are given by the following.
are given by the following.
![]()
![]()
![]()
Proof.![]() ,
, ![]() and
and ![]() similarly form in the classical case. Therefore
similarly form in the classical case. Therefore ![]() and
and ![]() are of same argument (cf. [13] ).
are of same argument (cf. [13] ).
Let E be a complex rank-![]() super vector bundle over a complex
super vector bundle over a complex ![]() -dimensional supermanifold
-dimensional supermanifold![]() . The total super Chern class is written by
. The total super Chern class is written by
![]()
Hence, we have
![]() ,
,
![]() ,
,
![]() ,
,
![]() .
.
The total super Pontrjagin class is written by
![]()
Hence, we have
![]() ,
,
![]() .
.
Then, they satisfy that
![]()
W
4. Riemann-Roch Type Formula
Let ![]() be the complex supercurves with genus g, where
be the complex supercurves with genus g, where![]() ,
, ![]() ,
,
in Example 2.1 (5). Then the canonical super line bundle on ![]() is explicitly written by
is explicitly written by
![]()
Hence we have![]() .
.
Note that for any object E and F the parity change functor ![]() satisfies
satisfies
![]()
In general, if ![]() is a supermanifold, then its tangent bundle can be written by
is a supermanifold, then its tangent bundle can be written by ![]() (cf. [16] ). Hence we have
(cf. [16] ). Hence we have
![]()
Using this decomposition, Euler number of ![]() get
get
![]()
Note that![]() .
.
Theorem 4.1 Let ![]() be the complex
be the complex ![]() -dimensional supercurves with genus g. Then, we have a Noether type formula as follows.
-dimensional supercurves with genus g. Then, we have a Noether type formula as follows.
![]()
Proof. Let ![]() be the genus on the classical Riemann surfaces and
be the genus on the classical Riemann surfaces and ![]() be
be
the number of linear independent Dirac zero modes or harmonic spinors which is not topologically invariant.
The structure sheaf of the complex supercurves have decomposition
![]() .
.
In the case of genus![]() , we have (cf. ([17] ))
, we have (cf. ([17] ))
![]()
In the case of genus![]() , it always satisfies
, it always satisfies ![]() for any p. In the case of genus
for any p. In the case of genus![]() , it satisfies
, it satisfies
![]()
In the case of genus![]() , we have the following.
, we have the following.
![]()
![]()
Note that equal of second make use of the classical Serre duality. Hence we obtain
![]()
In the case of genus ![]() and
and![]() , we can prove similarly. W
, we can prove similarly. W
Corollary 4.1 Let ![]() be the complex
be the complex ![]() -dimensional supercurves with genus g. Then we have a Riemann- Roch type formula as follows.
-dimensional supercurves with genus g. Then we have a Riemann- Roch type formula as follows.
![]()
where ![]() is the fundamental homology class.
is the fundamental homology class.
Proof.
![]()
From Theorem 4.1, this completes the proof of Corollary 4.1. W
The following Corollary essentially has been obtained by [18] . It needs the ![]() supersymmetric structure on the
supersymmetric structure on the ![]() super Riemann surfaces (cf. [7] [19] [20] ). The following rewrite the result of [21] to the super characteristic classes.
super Riemann surfaces (cf. [7] [19] [20] ). The following rewrite the result of [21] to the super characteristic classes.
Corollary 4.2 Let ![]() be the complex
be the complex ![]() -dimensional super Riemann surfaces and
-dimensional super Riemann surfaces and ![]() be any super line bundles of rank
be any super line bundles of rank ![]() on
on![]() . Then we have a Atiyah-Singer index type formula as follows.
. Then we have a Atiyah-Singer index type formula as follows.
![]()
where ![]() is the fundamental homology class.
is the fundamental homology class.
Proof. The canonical super line bundle ![]() of a super Riemann surface
of a super Riemann surface ![]() can be defined by splitting the Berezin bundle
can be defined by splitting the Berezin bundle ![]() using the super complex structure
using the super complex structure![]() . We get an exact sequence ([21] [22] )
. We get an exact sequence ([21] [22] )
![]()
We can define the operator![]() ,
, ![]() ,
, ![]() ,
,![]() . Note that the
. Note that the
operator ![]() is
is ![]() supersymmetric anti-holomorphic vector fields. Tensoring this exact sequence with any super line bundles
supersymmetric anti-holomorphic vector fields. Tensoring this exact sequence with any super line bundles![]() , we have
, we have
![]()
We can define the operator![]() ,
, ![]() ,
,![]() . We can describe
. We can describe ![]()
as the space of sections s of ![]() satisfying the condition
satisfying the condition![]() . The group
. The group ![]() can be described as
can be described as
the space of sections ![]() modulo the image of the operator
modulo the image of the operator![]() . Hence
. Hence ![]()
and![]() . W
. W
Let ![]() be
be ![]() distinct points and
distinct points and![]() ,
,![]() . Then the super meromorphic functions
. Then the super meromorphic functions
![]()
is coresponding to the super Weil divisor (cf. [18] [20] )
![]()
where ![]() is a super holomorphic function. We put
is a super holomorphic function. We put![]() ,
, ![]() ,
, ![]() and
and
![]() . Then the inverse element of
. Then the inverse element of![]() , which is unique, is given by the formula
, which is unique, is given by the formula ![]() (cf. [23] ). As an application, we have a main theorem as follows.
(cf. [23] ). As an application, we have a main theorem as follows.
Theorem 4.2 Let ![]() be the complex
be the complex ![]() -dimensional supercurves with genus g and
-dimensional supercurves with genus g and ![]() be
be
any super line bundles of rank ![]() on
on![]() . Then we have a Riemann-Roch type formula as follows.
. Then we have a Riemann-Roch type formula as follows.
![]()
where ![]() is the fundamental homology class.
is the fundamental homology class.
Proof. Let us consider the super divisor ![]() on
on![]() . The local equation on D is defined by
. The local equation on D is defined by ![]() on a open set
on a open set ![]() of
of![]() . If
. If![]() , then
, then![]() . The super Weil divisor can be considered as the super Cartier divisor. Then there is the exact sequence
. The super Weil divisor can be considered as the super Cartier divisor. Then there is the exact sequence
![]()
The line sheaf ![]() corresponding to
corresponding to ![]() is defined by the transition functions
is defined by the transition functions
![]()
on![]() . The sheaf
. The sheaf ![]() which is defined by
which is defined by
![]()
is the coherent ideal sheaf. The fiber ![]() of
of ![]() is of zero in
is of zero in ![]() and
and ![]() in
in![]() . The sheaf
. The sheaf ![]() is called the super skyscraper sheaf. Tensoring this with
is called the super skyscraper sheaf. Tensoring this with![]() , we have
, we have
![]()
The map ![]() is defined by
is defined by ![]() on an open set
on an open set ![]() of
of![]() . Taking co-
. Taking co-
homology, this gives a long exact sequence
![]()
Taking the alternative sum, we have
![]()
Noting that ![]() and
and![]() , we have
, we have
![]()
From ![]() and
and![]() , we have
, we have
![]()
We also take the exact sequence
![]()
This gives rise to a long exact sequence
![]()
Taking also the alternative sum, we have
![]()
Hence, we havet
![]()
Note that![]() . So adding
. So adding ![]() in both side, we see that
in both side, we see that
![]()
Therefore, ![]() is independent of
is independent of![]() , so that we can put
, so that we can put![]() .
.
From Theorem 6.1,![]() . This completes the proof of
. This completes the proof of
Theorem 4.2. W
5. Helicity Group
Definition 5.1 The helicity rank of finitely generated group G is defined by the positive generator of linearly independent itself. The helicity rank is denoted by![]() . The helicity rank of
. The helicity rank of ![]() is defined by the negative generator of linearly independent itself. The helicity rank of
is defined by the negative generator of linearly independent itself. The helicity rank of ![]() also is defined by twice the positive generator of linearly independent itself of G.
also is defined by twice the positive generator of linearly independent itself of G.
We define the finitely generated group of two type as follows.
![]()
![]()
Note that![]() ,
, ![]() and
and ![]() are isomorphic to
are isomorphic to![]() ,
, ![]() and
and ![]() as abelian groups, respectively.
as abelian groups, respectively.
But its helicity rank is differently as follows.
Example 5.1![]() ,
, ![]() ,
, ![]() ,
,
![]() , , , ,
, , , ,
![]() , ,.
, ,.
Definition 5.2 Let ![]() be a
be a ![]() -dimensional complex supermanifold. Then the helicity group
-dimensional complex supermanifold. Then the helicity group ![]() is defined by the following.
is defined by the following.
![]()
The helicity rank of ![]() can be represented by
can be represented by
![]()
The super cohomology with coefficient in ![]() of an
of an ![]() -dimensional supermanifold
-dimensional supermanifold ![]() is isomorphic to the
is isomorphic to the ![]() -valued cohomology with coefficient in
-valued cohomology with coefficient in ![]() of the classical manifold M using the universal coefficient theorem. That is to say, we have the following.
of the classical manifold M using the universal coefficient theorem. That is to say, we have the following.
![]()
This isomrphism is applied in section 6.
6. Gauss-Bonnet Type Formula
In this section, we will apply the super cohomology with coefficient in helicity group![]() .
.
Theorem 6.1 Let ![]() be the complex
be the complex ![]() -dimensional supercurves with genus g. Then we have a Gauss- Bonnet type formula as follows.
-dimensional supercurves with genus g. Then we have a Gauss- Bonnet type formula as follows.
![]()
Proof. Euler number of ![]() get
get
![]()
Note that![]() . On the other hand, the right hand side is
. On the other hand, the right hand side is
![]() .
.
Both sides coincide. W
Theorem 6.2 Let ![]() be the complex
be the complex ![]() -dimensional super projective space. Then, we have
-dimensional super projective space. Then, we have
![]()
Proof.
From the super Euler sequence, we can compute the total Chern class of holomorphic tangent bundle![]() . Setting
. Setting ![]() for simplicity’s sake and
for simplicity’s sake and![]() , we have
, we have
![]()
The sum of coefficient of x is the first super Chern number![]() .
.
![]() W.
W.