The Harmonic Neutron Hypothesis: Prime Number Factor Patterns and Their Relationship to the Hierarchy of the Fundamental Particles and Bosons ()
1. Introduction
1.1. Unresolved Pure Number Model of the Origin of the Physical Constant Hierarchy
The primary method organizing and conceptualizing the fundamental physical constants is the Standard Model, SM, (Table 1) [1] - [13] . The SM has had excellent success in many areas, but fails in defining a global system that spans the classic, quantum, and cosmic domains. String Theory, ST, has attempted to solve these issues for multiple decades as well, but has not succeeded either [14] [15] . A logical model explaining the global organization of the physical constants from a purely integer number property perspective does not exist.
Quantum physics demonstrates many pure number properties that are expressed simultaneously as physical characteristics, but this is the minority of all physical phenomena. There are many unanswered questions that go to the very heart of a system of physical constants for which there is no logical pure number structure. These questions include: Why are there are six leptons and six quarks? Why there are 3 up type quarks and 3 down type quarks? Why are there three charged leptons, and three with zero or minimal mass neutral leptons? Why do the quarks have fractional charges of ±1/3 and ±2/3? Why are the fundamental constants clustered around the relative mass of the neutron and become increasingly sparse as one moves away? Physicists know that black body radiation is integer-based harmonic system, but how are other particles and bosons scaled by an integer harmonic system? If the physical constants possess a numerically and computationally single pure number system what is its common organization? Why are some physical constants quantum in character and others apparently continuous? What has prevented many more physical systems from pure number representation?
1.2. Goal
The goal is to evaluate the prime numbers, prime factors, and their composite integers of the partial harmonic fractions derived from standard experimental data utilizing methods of the Harmonic Neutron Hypothesis, HNH. The HNH is a unified model associated with the some of the most important physical constants including particles and bosons, Table 1, Table 2. Most of these values have been previously published [16] - [22] . The prime
![]()
Table 1. The classic SM table of the fundamental constants labeled with the integer values derived from the HNH.
Table 1 is in the classic format of the principal physical phenomena of the Standard Model. Their quantum numbers, prime factors, and partial fractions are also listed. Each box lists the entity, sign, principal quantum number, harmonic fraction, 1/n, quantum fraction, qf, or partial fraction and as a product of harmonic numbers when applicable. All of the prime number factors are in bold. The prime products of the composite numbers are shown. The photon in this case is associated with the ionization energy of hydrogen and the number 3. The neutron gluons are associated with the partial fraction 47/48. The principal quantum number of α−1 is 11, as well as, the down quark, and H0.
![]()
![]()
Table 2. Experimental standard units and HNH units.
Table 2 lists the physical constants evaluated in this paper, principal quantum numbers, standard values, frequency equivalents, nie, nife, exponents known, δ, and the partial harmonic fractions.
factor patterns, using pure number properties elucidated by the HNH, are interrogated to see if they correlate and explain the known hierarchy and organization of the physical constants. The HNH is an innovative novel method to evaluate the relationships between the physical constants. Defining the origin of the SM organization would be a significant theoretical and computational advancement.
2. Methods
2.1. An Overview of the Harmonic Neutron Hypothesis
The following is a limited review and explanation of the HNH. The details have been described in multiple previous publications, and will not be repeated [16] - [22] . Our model is purely computational and finite integer based. The primary hypothesis is that the fundamental constants are inter-related by simple, ubiquitous mathematical and geometric integer patterns and properties. The HNH model has demonstrated new insights into some of these pure number issues. The HNH is a single natural unit harmonic system spanning different physical domains that is not possible using either the SM or ST models. Each physical state, distance, time, matter are defined with an integer scaled by the fundamental frequency,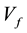 . Each observable physical constant is also associated with an integer described as a principal quantum number, n. This n defines a partial fraction,
. Each observable physical constant is also associated with an integer described as a principal quantum number, n. This n defines a partial fraction, 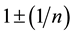 , that is an exponent of the
, that is an exponent of the . This integer is logically and computationally derived based on relative scale similar in concept to the chemical periodic chart. The physical constants must also follow power law properties within a harmonic system with the four natural unit values that scale the system, namely the neutron, n0, electron, e, Bohr radius,
. This integer is logically and computationally derived based on relative scale similar in concept to the chemical periodic chart. The physical constants must also follow power law properties within a harmonic system with the four natural unit values that scale the system, namely the neutron, n0, electron, e, Bohr radius, 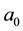 , Rydberg constant, R. The constants are associated within a classic resonant harmonic fraction,
, Rydberg constant, R. The constants are associated within a classic resonant harmonic fraction, 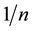 , and partial fraction,
, and partial fraction, 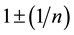 , system. The model has predictive power beyond standard methods by analyzing the whole system as an integrated spectrum rather than individual, isolated physical values. The methods of prediction are similar to standard methods utilized in quantum atomic spectra.
, system. The model has predictive power beyond standard methods by analyzing the whole system as an integrated spectrum rather than individual, isolated physical values. The methods of prediction are similar to standard methods utilized in quantum atomic spectra.
The model utilizes the dimensional analysis methods similar to that of Rayleigh and Buckingham’s Pi Theorem, where the exponential base is the dimensionless neutron annihilation frequency, 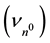 s equals
s equals 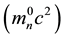 s/h, equals 2.2718590 (01) × 1023 Hz-s,
s/h, equals 2.2718590 (01) × 1023 Hz-s, 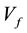 , and the harmonic partial fraction exponents are combinations of
, and the harmonic partial fraction exponents are combinations of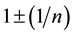 . This is related to neutron anti-neutron pair production, and the transformation of electromagnetic energy to matter within two interlocking consecutive integer series. These represent black body radiation and the elements. The model is a harmonic system so it must be a power law in both the linear and exponential domains for the states and constants respectively. The Buckingham Pi Theorem states that physical laws are independent
. This is related to neutron anti-neutron pair production, and the transformation of electromagnetic energy to matter within two interlocking consecutive integer series. These represent black body radiation and the elements. The model is a harmonic system so it must be a power law in both the linear and exponential domains for the states and constants respectively. The Buckingham Pi Theorem states that physical laws are independent
of the form of the physical units. Therefore, acceptable laws of physics are homogeneous in all dimensions. All of the physical phenomena are evaluated as frequency equivalents, and secondarily as dimensionless coupling constant ratios. The system is physical unit-independent. The fundamental frequency, 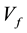 , ratio we use as a dimensionless number, is that scaled by the annihilation frequency of the neutron. This ratio is an invariant, independent of initial physical units utilized since it is by a single natural unit. The other units are 1 and drop out. Any single physical unit could be utilized, but Hertzian frequency (Hz) was arbitrarily chosen since the whole physical system can logically be evaluated as a unified quantum spectrum.
, ratio we use as a dimensionless number, is that scaled by the annihilation frequency of the neutron. This ratio is an invariant, independent of initial physical units utilized since it is by a single natural unit. The other units are 1 and drop out. Any single physical unit could be utilized, but Hertzian frequency (Hz) was arbitrarily chosen since the whole physical system can logically be evaluated as a unified quantum spectrum.
Our model has derived Planck’s time, tP, the Higgs boson, 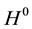 , the Hubble constant,
, the Hubble constant, 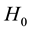 , the quark masses, the lost matter of neutron beta decay. Some of the HNH predictions exceed the precision of known experimental data currently available. It is not known, presently, whether any other method can generate derivable proportionality constants between these physical constants and the neutron, which are testable within power law methods. These predictions and derivation are from two (2) finite integer sets. The first set includes four natural units based on known atomic quantities as frequency equivalents. Included in this set is the neutron,
, the quark masses, the lost matter of neutron beta decay. Some of the HNH predictions exceed the precision of known experimental data currently available. It is not known, presently, whether any other method can generate derivable proportionality constants between these physical constants and the neutron, which are testable within power law methods. These predictions and derivation are from two (2) finite integer sets. The first set includes four natural units based on known atomic quantities as frequency equivalents. Included in this set is the neutron, ![]() , and comprises the
, and comprises the ![]() ratio of the system. A partition of this set includes the frequency equivalents of the electron, e, the Bohr radius,
ratio of the system. A partition of this set includes the frequency equivalents of the electron, e, the Bohr radius, ![]() , and the ionization energy of hydrogen, derived from the Rydberg constant, R. The second set of n numerator or denominator values is related to the partial fractions and includes: {1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12, 13, 23, 24, 27, 28, 32, 33, 47, 48, 109, 110}. These are all of the integers that define the constants evaluated.
, and the ionization energy of hydrogen, derived from the Rydberg constant, R. The second set of n numerator or denominator values is related to the partial fractions and includes: {1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12, 13, 23, 24, 27, 28, 32, 33, 47, 48, 109, 110}. These are all of the integers that define the constants evaluated.
The unit system of the HNH is simplified with the units for Planck’s constant, unit electric charge, time, the distance light travels in one unit of time, and the speed of light all equaling 1. All entities are defined as in terms of ratios and exponents of![]() . Energy, mass, frequency, temperature are all scaled equally. Distance defined as
. Energy, mass, frequency, temperature are all scaled equally. Distance defined as
1 divided by frequency. The speed of light equals ![]() times the distance
times the distance![]() , the Compton radius of the
, the Compton radius of the
neutron. In this type of single-variable physical system the units are all dimensionless coupling constants and completely defined by exponents or integer values of![]() .
.
The Equality Pair Transformations (EPTs), which we describe, inter-relate matter, electromagnetic energy, and kinetic energy transformations. These EPT are common physical phenomena, but necessitate a definitional approach when utilized in this model. Each EPT is associated with a point transformation from one state to another, or from one force to another, such as, kinetic energy to electromagnetic energy, electromagnetic energy to matter, or vice-versa. This occurs whenever there is a relative scale equality of two different states or forces. The pair is identically scaled phenomena, but can represent different (paired) physical manifestations of different forces or states. This is the essence of the particle-wave duality paradox. Examples are matter-antimatter pair production or annihilation; or the transformation of electromagnetic energy to kinetic energy as in the photoelectric effect. Not only is there a conservation-equality of total energy-matter, but also a transformation of state or force.
The primary fundamental EPT scaling in the HNH model is neutron anti-neutron pair production, and is the scaling factor used to derive further observable phenomena. The fundamental EPT ratio set is composed of a natural physical unit within a consecutive integer series, ![]() , representing the transformation of electromagnetic energy into frequency multiples of matter associated with neutron/anti-neutron pair production. The integrally spaced dimensionless elements,
, representing the transformation of electromagnetic energy into frequency multiples of matter associated with neutron/anti-neutron pair production. The integrally spaced dimensionless elements, ![]() derived from
derived from![]() , are based on the ratio of the respective annihilation frequencies of that physical constant to that of the neutron. The fundamental EPT is the point where the photon integral frequency series,
, are based on the ratio of the respective annihilation frequencies of that physical constant to that of the neutron. The fundamental EPT is the point where the photon integral frequency series, ![]() h, where h is Planck’s constant, has enough energy to be scaled identically with its elemental neutral matter equivalent, the neutron. The series restarts again at 1 with each integer,
h, where h is Planck’s constant, has enough energy to be scaled identically with its elemental neutral matter equivalent, the neutron. The series restarts again at 1 with each integer, ![]() , representing the number of nucleons in elemental matter or groups of nucleons.
, representing the number of nucleons in elemental matter or groups of nucleons.
2.2. Conversion of Physical Constants to Frequency Equivalents, Exponents, δ, and Partial Fractions
There are multiple possible integer “n’s” described in this model and they are differentiated. Integer exponents of ![]() are described as “nie”. Partial or harmonic integer fractional “n” exponent values are described as “nife”, whereas the “n” of the consecutive integer series are described as “
are described as “nie”. Partial or harmonic integer fractional “n” exponent values are described as “nife”, whereas the “n” of the consecutive integer series are described as “![]() ”. For example black body radiation energy equals
”. For example black body radiation energy equals ![]() (h).
(h).
All of the data for the fundamental constants were obtained from the websites: http://physics.nist.gov/cuu/Constants/ and www.wikipedia.org. The NIST site http://physics.nist.gov/cuu/Constants/energy.html has an online physical unit converter that can be used for these types of calculations so the values used in the model are all standard unit conversions.
The floating point (the number of accurate digits) is based upon known experimental atomic data, of approximately 5 × 10−8. All of the known fundamental constants are converted to frequency equivalents, vk. Equation (1) demonstrates the frequency equivalent conversion of the neutron as an example. Table 2 lists the standard unit, frequency equivalent, nie, nife, partial fraction, δ, and known exponents, expk of the constants evaluated in this paper. Conversation of the other constants have been previously published. Masses are converted by multiplying by c2 (speed of light squared) then dividing by h (Planck’s constant). Distances are converted by dividing the wavelength into c. Energies in Joules are converted to Hz by dividing by h. The eV value for the neutron is 939.565378 (21) × 106. Its frequency in Hz is converted to eV by multiplying by the constant, 4.13566750 (21) × 10?15 eV/Hz. The eV was converted to frequency by multiplying by the constant 2.41798930 (13) × 1014 Hz/eV.
![]() (1)
(1)
Though not intuitively obvious in this type of a defined single physical unit system, ![]() , is an invariant coupling constant independent of whatever physical unit system is initially chosen. This is a consequence of the definition since all of the constants are based on
, is an invariant coupling constant independent of whatever physical unit system is initially chosen. This is a consequence of the definition since all of the constants are based on ![]() which itself is a natural constant independent of physical unit. Any change in the initial arbitrary mass unit is canceled by a change in the value of an arbitrary Avogadro’s number NA. Any change in the arbitrary time or arbitrary distance units are canceled as well.
which itself is a natural constant independent of physical unit. Any change in the initial arbitrary mass unit is canceled by a change in the value of an arbitrary Avogadro’s number NA. Any change in the arbitrary time or arbitrary distance units are canceled as well.
This model has two parallel domains both describing identical physical values. One domain is the frequency equivalent of any physical value. This is the linear domain of possible physical states. The other domain is the
exponent of the base![]() , which when raised to that exponent equals the frequency equivalent of that spe-
, which when raised to that exponent equals the frequency equivalent of that spe-
cific value, Equation (2). The known exponent, expk, of a fundamental constant is the ratio of the loge of the fre-
quency equivalent, vks, divided by the![]() , Equation (2). Here,
, Equation (2). Here, ![]() equals 53.780055612
equals 53.780055612
(22). Subscript k denotes a known experimental value and subscript d represents a derived value.
![]() (2)
(2)
The known expk minus the quantum fraction, qf, or partial harmonic fraction equals the known![]() , Equation (3). A quantum fraction, qf, is a possible integer fractional exponent, not solely a partial fraction in some settings.
, Equation (3). A quantum fraction, qf, is a possible integer fractional exponent, not solely a partial fraction in some settings.
The known frequency equivalent of a constant, vk, is calculated by raising ![]() to the expk.
to the expk.
![]() (3)
(3)
Table 3 lists the physical constant, the associated prime factors, the partial fractions, and the composite (i.e. prime × prime) factors comprising the quarks. Table 4 lists the prime factors of the composite factors of the quarks. Table 5 lists the physical constant, prime factors, partial fractions, and composite factors for the alternating boson-lepton pattern.
3. Results
Table 1 lists the particles and bosons evaluated in the SM format. Table 2 lists the particles and bosons
![]()
Table 3. Prime factors and composite numbers of the quarks harmonic partial fractions.
Table 3 lists the prime number factors, the partial fractions, and composite product values of the quarks. There are many repeating progressions and patterns. All of them a based on the product of three prime factors from 2, 3, 5, 7, 11. The u, s, b, and t quarks all have even numbered denominators while the others have prime odd/ prime numbers in the denominators. The u, s, b quarks all have common factors of 2 and 3 with a progression of 5, 7, 11 for the third. The d, c, t quarks all have the same three common factors 2, 5, 11. These harmonic are the only possibilities that logically and mathematically can arise from these three prime factor combinations.
![]()
Table 4. Prime factors of the quarks.
Table 4 lists an array of the prime factors. *Associated with the quarks’ composite harmonic fractions. They demonstrate specific progressive patterns.
![]()
Table 5. prime factors of 2 and 3, and the alternating composite pattern of selected bosons and leptons.
Table 5 demonstrates an alternating pattern of the boson and lepton entities with an increasing exponent of 2 prime factors with the common prime factor of 3. The odd number exponents of 2 are leptons and the even number are bosons.
evaluated. Their standard unit values, frequency equivalents, vk, known exponents, expk, known deltas, δk, nie, nife, partial fractions, prime factors, composite factors, and inter-relationships are listed.
Each of the pure number properties of integers that define the HNH are manifest as the organization of physical systems. There are a number of consecutive integer series quantum systems. Black body radiation is one. The other is the chemical periodic chart. There are many others including Moseley’s law and the Rydberg series.
The observable physical constants are spaced in a classic partial fraction pattern around the neutron. The relative scale of the physical constants in a single physical unit are clustered near the neutron by unstable higher order quark baryons. The mesons and more massive leptons are next. The recent discovery of the Higgs boson falls precisely near a partial fraction, 12/11. The products of neutron beta decay including hydrogen are farther out. Finally cosmic background microwave radiation, 1/2, H0, −3/4, and tP squared, −128/35. The fundamental constants are only found near partial fraction values. Table 2 demonstrates the clear partial fraction pattern, as not coincidental.
The origin of the general numerical organization of the constants is defined by the pure number imperative of partial fractions and prime numbers. The only partial harmonic fractions composed of the consecutive prime numbers 2 and 3 are 2/3 and 3/2. This is the unique intersection of a system based on a consecutive integer series, partial fractions, and primes. These prime factors and their composite, 6, are logically assumed to represent the most important relationship defining the global hierarchy of the physical constants. There must be paired groups of 3 physical entities. The other option is 23 or 8. This assumption is supported since there are many examples of 2, 3, 6, 8, 12 physical entities defining an associated group. This pattern does define the global organization of the Standard Model, Table 1. There are 6 matter quarks and 6 anti-matter quarks, total 12. There are three quarks with mass more than the neutron and three less. There are 3 up type quarks and 3 down type quarks. Two thirds of the nife of the quarks are even, and one third are primes. There are 3 matter leptons and 3 anti-matter leptons, totaling 6. There are 3 charged leptons and 3 neutral leptons. Beta decay is associated with three matter components, and three kinetic energy components. Baryons are composed of 3 quarks. Mesons are composed of 2 quarks. Bosons are frequently paired, as in pair production. There are no single isolated quarks. The charges of the quarks are ±1/3, and ±2/3. The six (6) quarks have subatomic properties of up, down, strangeness, charmness, bottomness, or topness. There are three physical states: matter, distance and time. The Lorentz factors are associated with three different ratios of the three states, matter/distance, distance/time, and time/matter. The product of these three fractions is dimensionless. There are 8 gluons. When using the computational approach developed in the HNH model, the consecutive primes 2 and 3 and the perfect integer 6, are fundamental, and not coincidental to physical reality.
The quarks demonstrate a very specific prime factor progression Table 3, Table 4. Each of the quarks is associated with 3 prime factors from the set of primes that belong to {2, 3, 5, 7, 11}. All six have the factor 2. This is logical for a higher generation series. The u, s, b quarks all have common prime factors of 2 and 3. For u, s, and b quarks, each generation is associated with a progressively increasing numerical value of the third prime factor, either 5, 7, or 11. The higher the last prime factor the greater the mass. The d, c, t quarks are all related to common factors of 2, 5, 11. Both the denominator and the numerator of the partial fractions are composites from their associated three prime factors for that specific quark. The only partial fractions that are possible with the smallest number of prime factors, represent the actual known quark’s partial fractions based on the power law imperative [19] . The u, s, b, t quarks all have composite even denominators. The d, c quarks all have prime odd denominators. The quarks are also associated with δ lines with integer value factors {1,2,3} of the electromagnetic line slope of bem for their Y-axis intercepts, and -bem for their slopes. Here, bem is related to the slope of the electromagnetic δ-line related to R and h [16] [19] . The c, b, t quarks are associated with slope of 1(-bem), s and d quarks with slope 2(-bem), and u quark with slope 3(-bem). This is a quantum number discovered within the HNH.
There is a progression of a consecutive integer series of the powers of 2 in a composite product with 3 representing an alternating pattern (e.g. 2n × 3) of the most fundamental bosons and leptons, Table 5. Those entities with even number exponents of 2 are bosons, those with odd exponents of 2 are related to the weak force and leptons. These are all associated with charge, and the number 3 is associated with the ionization energy of hydrogen.
4. Discussion
4.1. Alternate Models Other than the Standard Model and String Theory Should Be Considered Valid
A robust model that accurately scales from classic, to quantum, to cosmic physical constants does not exist [14] [15] . The SM and ST have both failed in this regard. Despite these failures any other model, including the HNH, is almost universally met with derision, denial, and skepticism. Perhaps a new method should be considered based on past experience. An important unique aspect of the Harmonic Neutron Hypothesis is that it does resolve some of these limitations by analyzing the scaling relationships between the physical constants as a unified harmonic resonance finite integer prime-number-dominated power law system. Derivation of accurate quark masses, Planck time, the Hubble constant, and the Higgs boson from only sub-atomic natural physical units supports the validity of the model. There was no standard physical data specific to these entities used to derive their values. Every physical constant evaluated by the HNH model has been characterized by a derivable coupling constant with Vf.
Table 1 demonstrates the SM matrix of the physical constants including their principal number relationships. The HNH is a new unified perspective of the relationships of the fundamental constants to quantum numbers similar in concept to the chemical periodic chart. The hierarchy pattern of the composite and prime factors are not sums, but products. This is logical since the system is based on a resonant and harmonic system. This is typical in standard physical systems including music.
4.2. Pure Number Properties Manifest as Physical Properties
There are three primary number patterns inherent in the definition of the HNH that explain the most important patterns of the physical constants. First, is that all physical constants and possibly physical variables, which includes examples such as time, distance, or astronomically observable constants, are associated with a consecutive integer series. This accounts for many physical systems. Second, that many other physical constants are associated with partial harmonic fractions. This accounts for the clustering of the physical constants near the neutron scale, and increasingly sparse farther away, but in a very specific spacing pattern, Table 2. We are aware of no other model that shares this important attribute. The neutron represents the fundamental frequency of the system. The third is that not all possible integers, nife, represent observable physical constants, but only those that demonstrate harmonic resonant characteristics of the lower order prime factors. This pure number property is related to classic resonant properties of prime factor composites.
Pure number properties manifest physically in many quantum phenomena. These pure number properties are well established within a limited number of physics systems. The following are a few examples. Black body radiation, E equals ncish, and is associated with integer-valued frequencies. All elements are based on an integral number of nucleons. Both of these can appear continuous experimentally, but conceptually and mathematically they must be integer-based. Even numbers of protons and neutrons, within nucleons, are not associated with well-known nuclear magnetic resonance properties whereas those associated with odd numbers of nucleons are. The property of strangeness is integer-related as well. Charge is either integrally quantized, or fractional in units of 1/3 or 2/3. In this HNH model every possible degenerate mass, frequency, energy, temperature, distance, time, velocity, density, momentum is quantized, and defined by an integer in the collection of Vf.
4.3. Prime Number Manifestations within Physical Systems
There has been a long search for a clear example of the unequivocal dominance of primes manifest in a physical system [23] - [25] . There are a few examples, but the prime manifestations are obtuse. The first publication of the HNH demonstrated that the primes 3, R, 5, ![]() , 7, e, were clearly related to the properties of hydrogen [16] . Later papers demonstrated that 2 was related to the beta decay kinetic energy, and CMB. The prime 11 is related to the fine structure constant,
, 7, e, were clearly related to the properties of hydrogen [16] . Later papers demonstrated that 2 was related to the beta decay kinetic energy, and CMB. The prime 11 is related to the fine structure constant, ![]() , H0, and the down quark, respectively [21] . This paper demonstrates many of the clearest examples of the fundamental relationship of prime numbers and their composites to a physical system to date.
, H0, and the down quark, respectively [21] . This paper demonstrates many of the clearest examples of the fundamental relationship of prime numbers and their composites to a physical system to date.
The entire hierarchy of the organization and scaling of the physical constants is dominated by the smallest prime factors. The primes 2, 3, 5, 7, 11, 13, and 47 are associated with the first generation of particles and bosons, Table 1, Table 2. Two (2), the only even prime, is associated with kinetic energies including: lost kinetic energy of neutron beta decay, the electron anti-neutrino, and the peak spectral radiance of cosmic microwave background radiation, CMB. The number 2 is the most ubiquitous prime factor associated with every even composite. The next prime, 3, is associated with the Rydberg constant and the physical aspects of both charge and electromagnetic phenomena. We have found that 3 is also a factor of many of the bosons that are associated with charged entities. There are many examples of prime numbers related to their composites when forming partial harmonic fractions in the HNH model. The primes 13, 23, 47, and 109 are all drawn passively along with their smaller composite partners of 2, 3, 5, 7, 11.
4.4. Prime Factor Composite Manifestations of Physical Constants
There are also classic relationships of harmonic resonances defined by the product of common prime factors. These types of resonance patterns are ubiquitous in many physical systems, but they are not limited to prime fac- tors. This is not the case as demonstrated by the HNH for the hierarchy of the constants, which is inherently dependent upon the primes. The HNH demonstrates that there is a logical pure number explanation of the hierarchy of the fundamental particles and bosons, Tables 1-5.
The primary pure number property elucidated on previous published work using the HNH is that there is only one possible partial harmonic faction defined by the only possible consecutive primes, 2 and 3, namely 2/3. The factors, 2 and 3 as individual primes, products, and fractions define the global numerical hierarchy of the whole physical constant system, Tables 1-5. The higher order possibilities are defined by a series of logical progressions of products of lower prime factors. Table 3 and Table 4 demonstrate progressive patterns of smaller prime factors that define the only other possible composites that fulfill partial fraction relationships for the quarks. Table 5 demonstrates an alternating pattern of boson or lepton related to either an even or odd number exponent of the factor 2. Bosons are associated with pairs. Mesons are composed of 2 valence quarks. Anti-matter matter pair production is always associated with the prime, 2. Leptons and baryons are all associated with odd numbers. Three valence quarks form the standard baryons, and one entity for leptons.
Table 3 demonstrates an alternating pattern of prime factors of the quarks. There are three primes associated with each quark from the series: 2, 3, 5, 7, and 11. The first quark of each generation is associated with 2, 3 and one of the following primes 5, 7, 11. The second quark of each generation is composed only of factors 2, 5, and 11. There are a total of 6 primes that define the quarks including 109 which is passively related to the product of 2, 5, and 11. The products of the three primes must also simultaneously represent partial fractions where the composites must separate by 1. The actual partial fractions can be logically derived from the three prime series. The actual composites of the quarks represent the lowest possible number of factors, and the lowest possible primes. For example, for the primes 2, 3, 5, the up quark could be![]() , 9/10 or
, 9/10 or![]() , 15/16. The actual up quark is associated with 9/10, thus
, 15/16. The actual up quark is associated with 9/10, thus![]() . The other option of 15/16 has a total of four 2 factors and the composite of two higher primes, which logically would be associated with a higher order (mass or energy) entity. The actual prime factors follow a logical rule excluding certain possibilities as forbidden for specific generations.
. The other option of 15/16 has a total of four 2 factors and the composite of two higher primes, which logically would be associated with a higher order (mass or energy) entity. The actual prime factors follow a logical rule excluding certain possibilities as forbidden for specific generations.
There is no known physical entity associated with the partial fraction![]() . One is free to explore, using the tenets of the HNH, if such a numerical association defines a new entity. This may be true since three factors of 2 and two factors of 3 could both be associated with an undiscovered higher order entity, however, not one of the first generation as the present status of the HNH demonstrates.
. One is free to explore, using the tenets of the HNH, if such a numerical association defines a new entity. This may be true since three factors of 2 and two factors of 3 could both be associated with an undiscovered higher order entity, however, not one of the first generation as the present status of the HNH demonstrates.
If one carefully looks at the other three primes associated with the quarks there are no other possible combinations that can represent the known physical partial fractions starting with three primes. For example, the primes 2, 3, 7 are associated with the strange quark, 27/28. The other possible composites are 12 = (2 × 2 × 3), 14 = (2 × 7), 18 = (2 × 3 × 3), 21 = (3 × 7), 24 = (2 × 2 × 2 × 3), 36 = (2 × 2 × 3 × 3), 42 = (2 × 3 × 7), 49 = (7 × 7), 54 = (2 × 3 × 3 × 3), 63 = (3 × 3 × 7), 81 = (3 × 3 × 3 × 3). The associated n values of a partial fraction would have to be 11, 13, 15, 17, 19, 20, 22, 23, 25, 35, 37, 41, 43, 48, 50, 53, 55, 62, 64, 80, 82. It would be possible to generate the denominators for the partial fractions of 47/48 and 63/64 from 2 and/or 3, but there are many more prime factors. These should be associated with higher order entities. 27/28 is the lowest possible number of prime factors fulfilling the partial fraction imperative. The numerically restricted values defined by the prime factors and simultaneously defining a partial fraction represent actual physical values.
Many of the known exponents are not associated with their closest possible partial fraction. This manifestation is a demonstration that the actual partial fraction values must fulfill a prime product imperative [19] . The actual value of the ![]() shifts to maintain the expk. Good examples of this pattern are seen with the up, down, and strange quarks. Their
shifts to maintain the expk. Good examples of this pattern are seen with the up, down, and strange quarks. Their ![]() values are very small and quite distant from the X-axis. These δs are associated with multiple integer factors of the natural unit slope bem. The actual partial fractions and δ values all fulfill power law relationships with the natural unit values so they can be logically computed.
values are very small and quite distant from the X-axis. These δs are associated with multiple integer factors of the natural unit slope bem. The actual partial fractions and δ values all fulfill power law relationships with the natural unit values so they can be logically computed.
5. Conclusion
The properties of a consecutive integer series and a partial fraction series are both the primary organization and scaling of the fundamental physical constants. Pure prime number factor properties starting with 2 and 3, as the only possible prime partial harmonic fraction, define the dominant numerical hierarchy of groups of constants.
Acknowledgements
I would like to thank Richard White MD, Yu Ding PHD and Tom Budinger PHD for their support, and help.
NOTES
*Retired.