Time Scale Approach to One Parameter Plane Motion by Complex Numbers ()
1. Introduction
The calculus on time scales was initiated by B. Aulbach and S. Hilger in order to create a theory that can unify discrete and continuous analysis, [1] . Some preliminary definitions and theorems about delta derivative can be found in the references [2] - [4] .
In this study, some properties of motion in references [5] - [7] are investigated by using time scale complex planes. We find delta calculus equations of the motion and finally we get some results about the pole curves.
2. Preliminaries
A time scale is an arbitrary nonempty closed subset of the real numbers.
Definition 2.1. Let  be any time scale. The forward jump operator
be any time scale. The forward jump operator  is defined by
is defined by
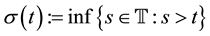
and the backward jump operator 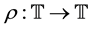 is defined by
is defined by

In this definition, we put  (i.e.
(i.e.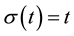 , if
, if 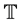 has a maximum t) and
has a maximum t) and 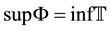 (i.e.
(i.e.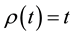 , if
, if  has a minimum t), where
has a minimum t), where ![]() denotes the empty set. If
denotes the empty set. If![]() , we say that t is right-scat- tered, while if
, we say that t is right-scat- tered, while if ![]() we say that t is left-scattered. Points that are right-scattered and left-scattered at the same time are called isolated. Also if
we say that t is left-scattered. Points that are right-scattered and left-scattered at the same time are called isolated. Also if ![]() and
and![]() , then t is called right-dense, and if
, then t is called right-dense, and if ![]() and
and![]() , then t is called left-dense. Points that are right-dense and left-dense at the same time are called dense.
, then t is called left-dense. Points that are right-dense and left-dense at the same time are called dense.
Finally, the graininess function ![]() is defined by
is defined by
![]()
If ![]() is a function, then we define the function
is a function, then we define the function ![]() by
by
![]()
Let us define the interior of ![]() relative to
relative to ![]() which is a function that maps
which is a function that maps ![]() into
into ![]() to be the set
to be the set
![]()
Definition 2.2. Assume ![]() is a function and let
is a function and let![]() . Then we define
. Then we define ![]() to be the number (pro- vided it exists) with the property that given any ε > 0, there is a neighborhood U of t (i.e.
to be the number (pro- vided it exists) with the property that given any ε > 0, there is a neighborhood U of t (i.e. ![]() for some
for some![]() ) such that
) such that
![]()
We call ![]() the delta (or Hilger) derivative of f at t. Moreover, we say that f is delta (or Hilger) differentiable on
the delta (or Hilger) derivative of f at t. Moreover, we say that f is delta (or Hilger) differentiable on ![]() provided
provided ![]() exists for all
exists for all![]() .
.
Theorem 2.1. Assume ![]() is a function and let
is a function and let![]() . Then we have the following:
. Then we have the following:
1) If f is differentiable at t, then f is continuous at t.
2) If f is continuous at t and t is right-scattered, then f is differentiable at t with
![]()
3) If t is right-dense, then f is differential at t if the limit
![]()
exists as a finite number. In this case a given
![]()
4) If f is differentiable at t then
![]()
Theorem 2.2. Assume ![]() are differentiable at
are differentiable at![]() . Then:
. Then:
1) The sum ![]() is differentiable at t with
is differentiable at t with
![]()
2) For any constant, ![]() is differentiable at t with
is differentiable at t with
![]()
3) The product ![]() is differentiable at t with
is differentiable at t with
![]()
4) If ![]() then
then ![]() is differentiable at t with
is differentiable at t with
![]()
5) If![]() , then
, then ![]() is differentiable at t with
is differentiable at t with
![]()
In the reference [3] , the chain rule on time scales is given for various cases.
Theorem 2.3. Assume ![]() is continuous,
is continuous, ![]() is delta differentiable on
is delta differentiable on![]() , and
, and ![]() is continuously differentiable. Then, there exists
is continuously differentiable. Then, there exists ![]() in the real interval
in the real interval ![]() with
with
![]()
Theorem 2.4. Let ![]() be continuously differentiable and suppose
be continuously differentiable and suppose ![]() is delta differentiable. Then
is delta differentiable. Then ![]() is delta differentiable and the formula
is delta differentiable and the formula
![]()
holds.
Theorem 2.5. Assume that ![]() is strictly increasing function and
is strictly increasing function and ![]() is a time scale. Let
is a time scale. Let![]() . If
. If ![]() and
and ![]() exist for
exist for![]() , then
, then
![]() (2.1)
(2.1)
Definition 2.3. For the given time scales ![]() and
and![]() , let us set
, let us set
![]() (2.2)
(2.2)
where ![]() is the imaginary unit. The set
is the imaginary unit. The set ![]() is called the time scale complex plane.
is called the time scale complex plane.
Definition 2.4. For![]() , we define the cylinder transformation
, we define the cylinder transformation ![]() by
by
![]()
and for![]() , let
, let![]() .
.
Definition 2.5. If![]() , then we define the exponential function by
, then we define the exponential function by
![]()
where the cylinder transformation ![]() is introduced in Definition 2.4.
is introduced in Definition 2.4.
Theorem 2.6. If ![]() then
then
1) ![]() and
and![]() ;
;
2)![]() ;
;
3)![]() ;
;
4)![]() ;
;
5)![]() ;
;
6)![]() ;
;
7)![]() ;
;
8)![]() ;
;
Theorem 2.7. Assume ![]() for
for ![]()
![]()
Theorem 2.8. If ![]() then
then
![]()
Theorem 2.9. If ![]() and
and ![]() then
then
![]()
3. One Parameter Motion and Hilger Complex Numbers on a Time Scale
Assume that ![]() is a time scale. Let us set the time scale complex plane for as
is a time scale. Let us set the time scale complex plane for as
![]() (3.1)
(3.1)
Here, let ![]() and
and ![]() be moving in a fixed time scale complex plane. The motion is called as one-parameter planar motion by the complex numbers on the time scale and denoted as
be moving in a fixed time scale complex plane. The motion is called as one-parameter planar motion by the complex numbers on the time scale and denoted as ![]() for a planar motion of E relative to E′.
for a planar motion of E relative to E′. ![]() and
and ![]() be their orthonormal frames, respectively. We suppose that
be their orthonormal frames, respectively. We suppose that ![]() is fixed, then we say that
is fixed, then we say that ![]() moves with respect to
moves with respect to![]() ,
, ![]() ,
, ![]() are the functions of a time scale parameter t. Let
are the functions of a time scale parameter t. Let ![]() and
and ![]() be the position vectors of a point X in the plane, as following we can write the coordinates of the point X by using complex numbers on the time scale with respect to a fixed or moving plane
be the position vectors of a point X in the plane, as following we can write the coordinates of the point X by using complex numbers on the time scale with respect to a fixed or moving plane ![]() and
and![]() , respectively. So:
, respectively. So:
![]()
The translation vector ![]() can be written as the following equation on a fixed plane
can be written as the following equation on a fixed plane![]() :
:
![]()
by using the definition of the time scale complex plane. The translation vector is more suitable as
![]()
for doing the formulas symmetric on the moving plane.
Thus, ![]() is equivalent to the vector
is equivalent to the vector![]() . Let
. Let ![]() be a rotation angle between the vectors
be a rotation angle between the vectors ![]() and
and ![]() (or the time scale complex planes
(or the time scale complex planes ![]() and
and![]() ), in Figure 1. So we can find the equation
), in Figure 1. So we can find the equation
![]()
Figure 1. One parameter planar motion on time scale.
![]() (3.2)
(3.2)
For any point![]() , the vector
, the vector ![]() is
is
![]() (3.3)
(3.3)
By substituting ![]() in the Equation (3.3)
in the Equation (3.3)
![]()
![]() (3.4)
(3.4)
Then, we can obtain the vector ![]() as follows:
as follows:
![]()
Here, assume the functions
![]()
are ![]() -differentiable functions and the parameter t is defined as
-differentiable functions and the parameter t is defined as ![]() on the
on the ![]() time scale. We will cal- culate the formulas for a fixed or moving plane.
time scale. We will cal- culate the formulas for a fixed or moving plane.
Definition 3.1. A velocity vector of the point X with respect to E is called ![]() -relative velocity vector of the point X on the time scale. The equation of relative
-relative velocity vector of the point X on the time scale. The equation of relative ![]() -velocity vector is
-velocity vector is
![]() (3.5)
(3.5)
for the moving time scale complex plane.
Definition 3.2. A velocity vector of the point X with respect to E is called ![]() -relative velocity vector of the point X on the time scale. The equation of the relative
-relative velocity vector of the point X on the time scale. The equation of the relative ![]() -velocity vector is
-velocity vector is
![]() (3.6)
(3.6)
![]() (3.7)
(3.7)
for the fixed time scale complex plane.
Definition 3.3. A velocity vector of the point X with respect to the time scale complex plane ![]() on the planar motion
on the planar motion ![]() which belongs to a curve
which belongs to a curve ![]() of the point
of the point ![]() on
on ![]() is called the
is called the ![]() -absolute velocity vector of the point X on the time scale and is denoted by
-absolute velocity vector of the point X on the time scale and is denoted by![]() .
.
Definition 3.4. On the planar motion![]() , while the point X is fixed on the moving time scale complex plane
, while the point X is fixed on the moving time scale complex plane ![]() (i.e.
(i.e.![]() ), a velocity vector of the point X is called the
), a velocity vector of the point X is called the ![]() -dragging velocity vector of this point on the time scale and is denoted by
-dragging velocity vector of this point on the time scale and is denoted by![]() .
.
So, we obtain the ![]() -absolute velocity
-absolute velocity![]() , i.e. the velocity of X with respect to the plane
, i.e. the velocity of X with respect to the plane![]() , from the Equation (3.4) using Equation (3.2).
, from the Equation (3.4) using Equation (3.2).
![]()
by Theorem 2.5. Also
![]()
and using Theorem 2.7, we have
![]()
Here, ![]() is called a delta-angular velocity of the motion
is called a delta-angular velocity of the motion ![]() on a time scale, and remembering Equations (3.3) and (3.7), we can find the dragging velocity vector
on a time scale, and remembering Equations (3.3) and (3.7), we can find the dragging velocity vector ![]() of the point X
of the point X
![]() (3.8)
(3.8)
![]() (3.9)
(3.9)
with the restriction![]() , from Equation (3.2) by taking the
, from Equation (3.2) by taking the ![]() -derivative with respect to the parameter t, we get the following equation.
-derivative with respect to the parameter t, we get the following equation.
![]()
and using Equation (3.2), we get
![]() (3.10)
(3.10)
Theorem 3.1. A ![]() -absolute velocity vector is equal to adding a
-absolute velocity vector is equal to adding a ![]() -relative velocity vector and
-relative velocity vector and ![]() -dragging velocity vector on the motion
-dragging velocity vector on the motion![]() , i.e.
, i.e.
![]() (3.11)
(3.11)
Proof. By using Equation (3.10) and Equation (3.5), we can get the following equations:
![]()
and thus, we get the relation of the velocities:
![]()
We have
![]()
We will calculate ![]() here using Equation (3.9) and Equation (3.10);
here using Equation (3.9) and Equation (3.10);
![]()
and
![]() (3.12)
(3.12)
Theorem 3.2. There is only one point at which the ![]() -dragging velocity is zero for any instant
-dragging velocity is zero for any instant![]() , i.e. which is fixed on the both of the planes
, i.e. which is fixed on the both of the planes ![]() and
and![]() , with the restriction
, with the restriction ![]() on the motion
on the motion![]() .
.
Proof. The points at which the ![]() -dragging velocity vector is zero for any instant
-dragging velocity vector is zero for any instant ![]() have to stay fixed for not only the plane
have to stay fixed for not only the plane![]() , but also for the plane
, but also for the plane ![]() on the motion
on the motion![]() . By taking
. By taking ![]() for fixed and moving planes, from (3.15) and (3.8):
for fixed and moving planes, from (3.15) and (3.8):
![]() (3.13)
(3.13)
![]() (3.14)
(3.14)
we can obtain the following complex vectors;
![]() (3.15)
(3.15)
![]() (3.16)
(3.16)
which are given ![]() -instantaneous rotation pole P on both coordinate systems. Because, the affine axioms
-instantaneous rotation pole P on both coordinate systems. Because, the affine axioms![]() ,
, ![]() are the end-points of
are the end-points of![]() ,
, ![]() , respectively.
, respectively.
Definition 3.5. The point ![]() which corresponds to the position vector
which corresponds to the position vector ![]() is called the for- ward pole or the instantaneous rotation pole or the instantaneous rotation center for the moving plane on the time scale motion
is called the for- ward pole or the instantaneous rotation pole or the instantaneous rotation center for the moving plane on the time scale motion![]() , in Figure 2.
, in Figure 2.
Definition 3.6. The point ![]() which corresponds to the position vector
which corresponds to the position vector ![]() is called the for- ward pole or the instantaneous rotation pole or the instantaneous rotation center for the fixed plane on the time scale motion
is called the for- ward pole or the instantaneous rotation pole or the instantaneous rotation center for the fixed plane on the time scale motion![]() , in Figure 2.
, in Figure 2.
We can get the following equations from Equation (3.15) and Equation (3.16):
![]() (3.17)
(3.17)
![]() (3.18)
(3.18)
By eliminating ![]() and
and ![]() from Equation (3.13) and Equation (3.14), the dragging velocity becomes as following:
from Equation (3.13) and Equation (3.14), the dragging velocity becomes as following:
![]() (3.19)
(3.19)
![]() (3.20)
(3.20)
and;
![]()
4. Conclusions
Result 4.1. Two results for the ![]() -dragging velocity of the point
-dragging velocity of the point ![]() on the moving plane can be obtained as follows:
on the moving plane can be obtained as follows:
1) Since scalar product of the vector is
![]()
and the vector ![]() is zero, these vectors are perpendicular.
is zero, these vectors are perpendicular.
2) The length of the vector ![]() can be calculated as follows:
can be calculated as follows:
![]()
here ![]() denotes for the length of
denotes for the length of![]() . From this result, we get the following theorem:
. From this result, we get the following theorem:
Theorem 4.1. On the motion![]() , the points X of the moving plane E draw trajectories on the fixed time scale complex plane
, the points X of the moving plane E draw trajectories on the fixed time scale complex plane ![]() which their normals (trajectory normals) pass from the instantaneous rotation pole
which their normals (trajectory normals) pass from the instantaneous rotation pole![]() .
.
Theorem 4.2. Every point of X of the moving plane E is doing rotational movement (instantaneous rotation movement) with a ![]() -centered,
-centered, ![]() -angular velocity and p factor on instant t.
-angular velocity and p factor on instant t.
Since X is an arbitrary point of the time scale complex plane E, we can give the following theorem:
Theorem 4.3. A one-parameter motion consists of rotation with ![]() angular velocity and p factor around the instantaneous rotation pole
angular velocity and p factor around the instantaneous rotation pole ![]() of the moving plane E on t instant, i.e. the plane E rotates with the angle
of the moving plane E on t instant, i.e. the plane E rotates with the angle ![]() and the factor p around the point
and the factor p around the point ![]() on the time element
on the time element![]() .
.
Theorem 4.4. The velocity vectors of the instantaneous rotation pole ![]() which draws the forward pole curves on the moving and fixed planes is the same vector at each instant t.
which draws the forward pole curves on the moving and fixed planes is the same vector at each instant t.
Theorem 4.5. On one-parameter planar motion ![]() the moving pole curve
the moving pole curve ![]() of the plane E rolls onto the fixed pole curve
of the plane E rolls onto the fixed pole curve ![]() of the plane
of the plane ![]() without sliding.
without sliding.
Result 4.2. Without being depended on time, a motion ![]() occurs by rolling, without sliding, the curve
occurs by rolling, without sliding, the curve ![]() of E onto the curve
of E onto the curve ![]() of
of![]() .
.