1. Introduction
It is well known that the notion of convexity plays a key role in optimization theory [1] [2] . In the literature, various generalizations of convexity have been considered. One such generalization is that of a  -convex function introduced by Vial [3] . Hanson and Mond [4] defined the notion of an F-convex function. As an extended unification of the two concepts, Preda [5] introduced the concept of a
-convex function introduced by Vial [3] . Hanson and Mond [4] defined the notion of an F-convex function. As an extended unification of the two concepts, Preda [5] introduced the concept of a 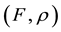 -convex function. Antczak gave the notion of a locally Lipschitz
-convex function. Antczak gave the notion of a locally Lipschitz 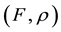 -convex scalar function of order k [6] and a differentiable
-convex scalar function of order k [6] and a differentiable  - convex vector function of order 2 [7] .
- convex vector function of order 2 [7] .
L. Cromme [8] defined the concept of a strict local minimizer of order k for a scalar optimization problem. This concept plays a fundamental role in convergence analysis of iterative numerical methods [8] and in stability results [9] . The definition of a strict local minimizer of order 2 is generalized to the vectorial case by Antczak [7] .
Recently, Bhatia and Sahay [10] introduced the concept of a higher-order strict minimizer with respect to a nonlinear function for a differentiable multiobjective optimization problem. They proved various sufficient optimality and mixed duality results involving generalized higher-order strongly invex functions.
The main purpose of this paper is to extend the concept of a higher-order minimizer to a nonsmooth vector optimization problem over cones. The paper is organized as follows. We begin in Section 2 by recalling some known concepts in the literature. We then define the notion of a (weak) minimizer of order k for a nonsmooth vector optimization problem over cones. Thereafter, we introduce various new generalized classes of cone- nonsmooth 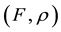 -convex functions of higher-order. In Section 3, we study several optimality conditions for higher-order minimizers via the introduced classes of functions. In Section 4, we associate a unified dual to the considered problem and establish weak and strong duality results.
-convex functions of higher-order. In Section 3, we study several optimality conditions for higher-order minimizers via the introduced classes of functions. In Section 4, we associate a unified dual to the considered problem and establish weak and strong duality results.
2. Preliminaries and Definitions
Let 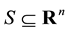 be a nonempty open subset of
be a nonempty open subset of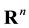 . Let
. Let 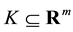 be a closed convex cone with nonempty interior and let
be a closed convex cone with nonempty interior and let  denote the interior of K. The dual cone K* of K is defined as
denote the interior of K. The dual cone K* of K is defined as
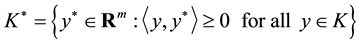 .
.
The strict positive dual cone 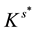 of K is given by
of K is given by
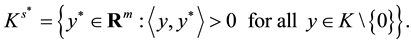
A function  is said to be locally Lipschitz at a point
is said to be locally Lipschitz at a point  if for some
if for some ,
,
![]()
![]() ,
, ![]() within a neighbourhood of u.
within a neighbourhood of u.
A function ![]() is said to be locally Lipschitz on S if it is locally Lipschitz at each point of S.
is said to be locally Lipschitz on S if it is locally Lipschitz at each point of S.
Definition 2.1. [11] Let ![]() be a locally Lipschitz function, then
be a locally Lipschitz function, then ![]() denotes the Clarke’s generalized directional derivative of
denotes the Clarke’s generalized directional derivative of ![]() at
at ![]() in the direction
in the direction ![]() and is defined as
and is defined as
![]() .
.
The Clarke’s generalized gradient of ![]() at u is denoted by
at u is denoted by ![]() and is defined as
and is defined as
![]() .
.
Let ![]() be a vector valued function given by
be a vector valued function given by ![]() ,
,![]() . Then f is said to be locally Lipschitz on S if each
. Then f is said to be locally Lipschitz on S if each ![]() is locally Lipschitz on S. The generalized directional derivative of a locally Lipschitz function
is locally Lipschitz on S. The generalized directional derivative of a locally Lipschitz function ![]() at
at ![]() in the direction
in the direction ![]() is given by
is given by
![]() .
.
The generalized gradient of f at u is the set
![]() ,
,
where ![]() is the generalized gradient of
is the generalized gradient of ![]() at u for
at u for![]() .
.
Every element ![]() is a continuous linear operator from
is a continuous linear operator from ![]() to
to ![]() and
and
![]() for all.
for all.
A functional ![]() is sublinear with respect to the third variable if, for all
is sublinear with respect to the third variable if, for all![]() ,
,
(i) ![]() for all
for all![]() , and
, and
(ii) ![]() for all
for all![]() .
.
(i) and (ii) together imply![]() . (1)
. (1)
We consider the following nonsmooth vector optimization problem
(NVOP) K-minimize ![]()
subject to![]() ,
,
where![]() :
:![]() ,
,![]() :
:![]() , K and Q are closed convex cones with nonempty interiors in Rm and Rp respectively. We assume that
, K and Q are closed convex cones with nonempty interiors in Rm and Rp respectively. We assume that ![]() for each
for each ![]() and
and ![]() for each
for each ![]() are locally Lipschitz on S.
are locally Lipschitz on S.
Let ![]() denote the set of all feasible solutions of (NVOP).
denote the set of all feasible solutions of (NVOP).
The following solution concepts are well known in the literature of vector optimization theory.
Definition 2.2. A point![]() , is said to be
, is said to be
(i) a weak minimizer (weakly efficient solution) of (NVOP) if for every![]() ,
,
![]()
(ii) a minimizer (efficient solution) of (NVOP) if for every![]() ,
,
![]()
With the idea of analyzing the convergence and stability of iterative numerical methods, L. Cromme [8] introduced the notion of a “strict local minimizer of order k”. As a recent advancement on this platform, Bhatia and Sahay [10] defined the concept of a higher-order strict minimizer with respect to a nonlinear function for a differentiable multiobjective optimization problem. We now generalize this concept and give the definition of a higher-order (weak) minimizer with respect to a function ![]() for a nonsmooth vector optimization problem over cones.
for a nonsmooth vector optimization problem over cones.
Definition 2.3. A point ![]() is said to be
is said to be
(i) a weak minimizer of order ![]() for (NVOP) with respect to
for (NVOP) with respect to![]() , if there exists a vector
, if there exists a vector ![]() such that, for every
such that, for every ![]()
![]() ;
;
(ii) a minimizer of order ![]() for (NVOP) with respect to
for (NVOP) with respect to![]() , if there exists a vector
, if there exists a vector ![]() such that, for every
such that, for every ![]()
![]()
Remark 2.1. (1) If f is a scalar valued function, ![]() and
and![]() , the definition of a weak minimizer of order k reduces to the definition of a strict minimizer of order k (see [8] [9] [12] [13] ).
, the definition of a weak minimizer of order k reduces to the definition of a strict minimizer of order k (see [8] [9] [12] [13] ).
(2) If![]() ,
, ![]() and
and![]() , the definition of a (weak) minimizer of order k becomes the definition of a vector strict global (weak) minimizer of order 2 given by Antczak [7] .
, the definition of a (weak) minimizer of order k becomes the definition of a vector strict global (weak) minimizer of order 2 given by Antczak [7] .
(3) If ![]() the definition of a weak minimizer of order k reduces to the definition of a strict minimizer of order k given by Bhatia and Sahay [10] .
the definition of a weak minimizer of order k reduces to the definition of a strict minimizer of order k given by Bhatia and Sahay [10] .
Remark 2.2. (1) Clearly a minimizer of order k for (NVOP) with respect to ![]() is also a weak minimizer of order k for (NVOP) with respect to the same
is also a weak minimizer of order k for (NVOP) with respect to the same![]() .
.
(2) A direct implication of the fact that ![]() is that, a (weak) minimizer of order k for (NVOP) with respect to
is that, a (weak) minimizer of order k for (NVOP) with respect to ![]() is a (weak) minimizer for (NVOP).
is a (weak) minimizer for (NVOP).
(3) Note that if ![]() is a (weak) minimizer of order k for (NVOP) with respect to
is a (weak) minimizer of order k for (NVOP) with respect to![]() , then for all
, then for all![]() , it is also a (weak) minimizer of order
, it is also a (weak) minimizer of order ![]() for (NVOP) with respect to the same
for (NVOP) with respect to the same![]() .
.
In the sequel, for a vector function ![]() and
and![]() ,
, ![]() denotes the vector
denotes the vector![]() .
.
We now define various classes of nonsmooth ![]() -convex functions of higher-order over cones.
-convex functions of higher-order over cones.
Definition 2.4. A locally Lipschitz function ![]() is said to be K-nonsmooth
is said to be K-nonsmooth ![]() -convex of order k with respect to
-convex of order k with respect to ![]() at
at ![]() on S if there exist a sublinear (with respect to the third variable) functional
on S if there exist a sublinear (with respect to the third variable) functional ![]() and a vector
and a vector ![]() such that, for each
such that, for each ![]() and all
and all ![]()
![]() .
.
If the above relation holds for every ![]() then f is said to be K-nonsmooth
then f is said to be K-nonsmooth ![]() -convex of order k with respect to
-convex of order k with respect to ![]() on S.
on S.
Remark 2.3. (1) If f is a scalar valued function and![]() , the above definition reduces to the definition of a (locally Lipschitz)
, the above definition reduces to the definition of a (locally Lipschitz) ![]() -convex function of order k with respect to
-convex function of order k with respect to ![]() given by Antczak [6] .
given by Antczak [6] .
(2) If f is a differentiable function, ![]() ,
, ![]() and
and ![]() the definition of a K-nonsmooth
the definition of a K-nonsmooth ![]() -convex function of order k with respect to
-convex function of order k with respect to ![]() becomes the definition of a vector
becomes the definition of a vector ![]() -convex function of order 2 given in [7] .
-convex function of order 2 given in [7] .
(3) If![]() ,
, ![]() for some function
for some function ![]() and
and![]() , K-nonsmooth
, K-nonsmooth ![]() - convexity of order k with respect to
- convexity of order k with respect to ![]() reduces to
reduces to ![]() -invexity, where
-invexity, where![]() , introduced by Nahak and Mohapatra [14] .
, introduced by Nahak and Mohapatra [14] .
(4) If ![]() is a differentiable function,
is a differentiable function, ![]() and
and![]() ,
, ![]() , for some function
, for some function![]() , the above definition becomes the definition of a higher-order strongly invex function given by Bhatia and Sahay [10] .
, the above definition becomes the definition of a higher-order strongly invex function given by Bhatia and Sahay [10] .
Definition 2.5. A locally Lipschitz function ![]() is said to be K-nonsmooth
is said to be K-nonsmooth ![]() -pseudoconvex type I of order k with respect to
-pseudoconvex type I of order k with respect to ![]() at
at ![]() on S if there exist a sublinear (with respect to the third variable) functional
on S if there exist a sublinear (with respect to the third variable) functional ![]() and a vector
and a vector ![]() such that, for each
such that, for each ![]() and all
and all![]() ,
,
![]() .
.
Equivalently,
![]() .
.
If f is K-nonsmooth ![]() -pseudoconvex type I of order k with respect to
-pseudoconvex type I of order k with respect to ![]() at every
at every ![]() then f is said to be K-nonsmooth
then f is said to be K-nonsmooth ![]() -pseudoconvex type I of order k with respect to
-pseudoconvex type I of order k with respect to ![]() on S.
on S.
Clearly, if f is K-nonsmooth ![]() -convex of order k with respect to
-convex of order k with respect to![]() , then f is K-nonsmooth
, then f is K-nonsmooth ![]() - pseudoconvex type I of order k with respect to the same
- pseudoconvex type I of order k with respect to the same![]() , however the converse may not be true as shown by the following example.
, however the converse may not be true as shown by the following example.
Example 2.1. Consider the following nonsmooth function![]() ,
, ![]() ,
, ![]() and
and ![]()
![]()
Here ![]() and
and![]() .
.
Define ![]() as
as
![]() .
.
Let ![]() be given by
be given by![]() ,
, ![]() and
and![]() .
.
Then, at![]() .
.
![]() ,
,
for every ![]() and
and![]() .
.
Hence, f is K-nonsmooth ![]() -pseudoconvex type I of order 3 with respect to
-pseudoconvex type I of order 3 with respect to ![]() at u on S.
at u on S.
However, for ![]() and
and![]() .
.
![]() ,
,
so that f is not K-nonsmooth ![]() -convex of order 3 at u on S.
-convex of order 3 at u on S.
Definition 2.6. A locally Lipschitz function ![]() is said to be K-nonsmooth
is said to be K-nonsmooth ![]() -pseudoconvex type II of order k with respect to
-pseudoconvex type II of order k with respect to ![]() at
at ![]() on S if there exist a sublinear (with respect to the third variable) functional
on S if there exist a sublinear (with respect to the third variable) functional ![]() and a vector
and a vector ![]() such that, for each
such that, for each ![]() and all
and all![]() ,
,
![]()
Equivalently,
![]() .
.
If the above relation holds for every![]() , then f is said to be K-nonsmooth
, then f is said to be K-nonsmooth ![]() -pseudoconvex type II of order k with respect to
-pseudoconvex type II of order k with respect to ![]() on S.
on S.
We now give an example to show that a K -nonsmooth ![]() -pseudoconvex type II function of order k with respect to
-pseudoconvex type II function of order k with respect to ![]() may fail to be a K -nonsmooth
may fail to be a K -nonsmooth ![]() -convex function of order k with respect to
-convex function of order k with respect to![]() .
.
Example 2.2. Consider the following nonsmooth function![]() ,
, ![]() ,
, ![]() and
and ![]()
![]() ,
,
Here ![]() and
and![]() .
.
Let ![]() be given by
be given by![]() .
.
![]() and.
and.
Then, at![]() ,
,
![]() ,
,
for every![]() ,
, ![]() and
and![]() .
.
Therefore, f is K-nonsmooth ![]() -pseudoconvex type II of order
-pseudoconvex type II of order ![]() with respect to
with respect to ![]() at u on S.
at u on S.
However, for ![]() and
and![]() ,
, ![]() ,
,
![]() .
.
Thus, f is not K-nonsmooth ![]() -convex of any order k with respect to
-convex of any order k with respect to ![]() at u on S.
at u on S.
Definition 2.7. A locally Lipschitz function ![]() is said to be K-nonsmooth
is said to be K-nonsmooth ![]() -quasiconvex type I of order k with respect to
-quasiconvex type I of order k with respect to ![]() at
at ![]() on S if there exist a sublinear (with respect to the third variable) functional
on S if there exist a sublinear (with respect to the third variable) functional ![]() and a vector
and a vector ![]() such that, for each
such that, for each ![]() and all
and all![]() ,
,
![]() .
.
If the above relation holds at every![]() , then f is said to be K-nonsmooth
, then f is said to be K-nonsmooth ![]() -quasiconvex type I of order k with respect to
-quasiconvex type I of order k with respect to ![]() on S.
on S.
Definition 2.8. A locally Lipschitz function ![]() is said to be K-nonsmooth
is said to be K-nonsmooth ![]() -quasiconvex type II of order k with respect to
-quasiconvex type II of order k with respect to ![]() at
at ![]() on S if there exist a sublinear (with respect to the third variable) functional
on S if there exist a sublinear (with respect to the third variable) functional ![]() and a vector
and a vector ![]() such that, for each
such that, for each ![]() and all
and all![]() ,
,
![]() .
.
If f is K-nonsmooth ![]() -quasiconvex type II of order k with respect to
-quasiconvex type II of order k with respect to ![]() at every
at every![]() , then f is said to be K-nonsmooth
, then f is said to be K-nonsmooth ![]() -quasiconvex type II of order k with respect to
-quasiconvex type II of order k with respect to ![]() on S.
on S.
Remark 2.4. When f is a differentiable function, ![]() and
and![]() ,
, ![]() for some function
for some function![]() , Definition 2.4 - 2.7 take the form of the corresponding definitions given by Bhatia and Sahay [10] .
, Definition 2.4 - 2.7 take the form of the corresponding definitions given by Bhatia and Sahay [10] .
3. Optimality
In this section, we obtain various nonsmooth Fritz John type and Karush-Kuhn-Tucker (KKT) type necessary and sufficient optimality conditions for a feasible solution to be a (weak) minimizer of order k for (NVOP).
On the lines of Craven [15] we define Slater-type cone constraint qualification as follows:
Definition 3.1. The problem (NVOP) is said to satisfy Slater-type cone constraint qualification at ![]() if, for all
if, for all![]() , there exists a vector
, there exists a vector ![]() such that
such that![]() .
.
Remark 3.1. The following inclusion relation is worth noticing.
For ![]() and
and![]() ,
,
![]()
Thus,
![]() . (2)
. (2)
Since a weak minimizer of order ![]() for (NVOP) is a weak minimizer for (NVOP), the following nonsmooth Fritz John type necessary optimality conditions can be easily obtained from Craven [15] .
for (NVOP) is a weak minimizer for (NVOP), the following nonsmooth Fritz John type necessary optimality conditions can be easily obtained from Craven [15] .
Theorem 3.1. If a vector ![]() is a weak minimizer of order k with respect to
is a weak minimizer of order k with respect to ![]() for (NVOP) with
for (NVOP) with![]() , then there exist Lagrange multipliers
, then there exist Lagrange multipliers ![]() and
and ![]() not both zero, such that
not both zero, such that
![]()
![]() .
.
The necessary nonsmooth KKT type optimality conditions for (NVOP) can be given in the following form.
Theorem 3.2. If a vector ![]() is a weak minimizer of order k with respect to
is a weak minimizer of order k with respect to ![]() for (NVOP) with
for (NVOP) with ![]() and if Slater-type cone constraint qualification holds at
and if Slater-type cone constraint qualification holds at![]() , then there exist Lagrange multipliers
, then there exist Lagrange multipliers ![]() and
and![]() , such that
, such that
![]() (3)
(3)
![]() . (4)
. (4)
Proof. Assume that ![]() is a weak minimizer of order k with respect to
is a weak minimizer of order k with respect to ![]() for (NVOP), then by Theorem 3.1 there exist
for (NVOP), then by Theorem 3.1 there exist ![]() and
and![]() , not both zero, such that (3) and (4) hold.
, not both zero, such that (3) and (4) hold.
If possible, suppose![]() . Then,
. Then, ![]() and (3) reduces to
and (3) reduces to
![]() .
.
So there exists ![]() such that
such that
![]() . (5)
. (5)
Now, since Slater-type cone constraint qualification holds at![]() , we have for all
, we have for all![]() , there exists a vector
, there exists a vector ![]() such that
such that![]() . Since
. Since![]() , we get
, we get![]() . In particular,
. In particular,![]() . On the contrary (5) implies
. On the contrary (5) implies![]() . This contradiction justifies
. This contradiction justifies![]() .
.
Now, we give sufficient optimality conditions for a feasible solution to be a higher-order (weak) minimizer for (NVOP).
Theorem 3.3. Let ![]() be a feasible solution for (NVOP) and suppose there exist vectors
be a feasible solution for (NVOP) and suppose there exist vectors![]() ,
, ![]() and
and![]() ,
, ![]() such that
such that
![]() (6)
(6)
![]() . (7)
. (7)
Further, assume that f is K-nonsmooth ![]() -convex of order k with respect to
-convex of order k with respect to ![]() at
at ![]() on
on ![]() and g is Q-nonsmooth
and g is Q-nonsmooth ![]() -convex of order k with respect to the same
-convex of order k with respect to the same ![]() at
at ![]() on
on![]() . If
. If ![]() and
and![]() , then
, then ![]() is a weak minimizer of order k with respect to
is a weak minimizer of order k with respect to ![]() for (NVOP).
for (NVOP).
Proof. Assume on the contrary that ![]() is not a weak minimizer of order k with respect to
is not a weak minimizer of order k with respect to ![]() for (NVOP). Then, for any
for (NVOP). Then, for any![]() , there exists a vector
, there exists a vector ![]() such that,
such that,
![]() .
.
As![]() , the above relation holds in particular for
, the above relation holds in particular for![]() , so that we have
, so that we have
![]() . (8)
. (8)
As (6) holds, there exist ![]() and
and ![]() such that
such that
![]() . (9)
. (9)
Since f is K-nonsmooth ![]() -convex of order k with respect to
-convex of order k with respect to ![]() at
at ![]() on
on![]() , we have
, we have
![]() . (10)
. (10)
Adding (8) and (10), we get
![]() .
.
As![]() , we obtain
, we obtain
![]() . (11)
. (11)
Also, since g is Q-nonsmooth ![]() convex of order k with respect to
convex of order k with respect to ![]() at
at ![]() on
on ![]() and
and![]() , we have
, we have
![]() .
.
However, ![]() ,
, ![]() and (7) together give
and (7) together give
![]() . (12)
. (12)
Adding (11) and (12), we get
![]() ,
,
which implies that
![]() .
.
Using sublinearity of F under the assumption ![]() and
and![]() , we obtain
, we obtain
![]() ,
,
which on using (9) and (1), gives
![]() .
.
This is impossible as ![]() and
and![]() , so that
, so that![]() , and norm is a non-negative function. Hence
, and norm is a non-negative function. Hence ![]() is a weak minimizer of order
is a weak minimizer of order ![]() with respect to
with respect to ![]() for (NVOP).
for (NVOP).
Theorem 3.4. Suppose there exists a feasible solution ![]() for (NVOP) and vectors
for (NVOP) and vectors ![]() and
and ![]() such that (6) and (7) hold. Moreover, assume that f is K-nonsmooth
such that (6) and (7) hold. Moreover, assume that f is K-nonsmooth ![]() -pseudoconvex type I of order k with respect to
-pseudoconvex type I of order k with respect to ![]() at
at ![]() on
on ![]() and
and ![]() is
is ![]() -nonsmooth
-nonsmooth ![]() -quasiconvex type I of order k with respect to the same
-quasiconvex type I of order k with respect to the same ![]() at
at ![]() on
on![]() . If
. If ![]() and
and![]() , then
, then ![]() is a weak minimizer of order k with respect to
is a weak minimizer of order k with respect to ![]() for (NVOP).
for (NVOP).
Proof: Let if possible, ![]() be not a weak minimizer of order k with respect to ω for (NVOP). Then, for any
be not a weak minimizer of order k with respect to ω for (NVOP). Then, for any![]() , there exists
, there exists ![]() such that,
such that,
![]() .
.
Since ![]() taking, in particular,
taking, in particular, ![]() in the above relation, we obtain
in the above relation, we obtain
![]() . (13)
. (13)
As (6) holds, there exist ![]() and
and ![]() such that (9) holds.
such that (9) holds.
Since f is K-nonsmooth ![]() -pseudoconvex type I of order k with respect to ω at
-pseudoconvex type I of order k with respect to ω at ![]() on
on![]() , (13) implies
, (13) implies
![]() .
.
As![]() , we have
, we have
![]() . (14)
. (14)
Now, ![]() means
means![]() , so that
, so that![]() . This along with (7) gives
. This along with (7) gives
![]() . (15)
. (15)
If![]() , then (15) implies
, then (15) implies![]() .
.
Since g is Q-nonsmooth ![]() -quasiconvex type I of order k with respect to
-quasiconvex type I of order k with respect to ![]() at
at ![]() on
on![]() , therefore
, therefore
![]() ,
,
so that
![]() . (16)
. (16)
If![]() , then also (16) holds.
, then also (16) holds.
Now, proceeding as in Theorem 3.3, we get a contradiction. Hence, ![]() is a weak minimizer of order k with respect to
is a weak minimizer of order k with respect to ![]() for (NVOP).
for (NVOP).
Theorem 3.5. Assume that all the conditions of Theorem 3.3 (Theorem 3.4) hold with![]() . Then
. Then ![]() is a minimizer of order k with respect to
is a minimizer of order k with respect to ![]() for (NVOP).
for (NVOP).
Proof: Let if possible, ![]() be not a minimizer of order k with respect to
be not a minimizer of order k with respect to ![]() for (NVOP), then for any
for (NVOP), then for any ![]() there exists
there exists ![]() such that
such that
![]() . (17)
. (17)
Proceeding on similar lines as in proof of Theorem 3.3 (Theorem3.4) and using (17) we have
![]() .
.
As![]() , we get
, we get
![]() .
.
This leads to a contradiction as in Theorem 3.3 (Theorem 3.4). Hence, ![]() is a minimizer of order k with respect to
is a minimizer of order k with respect to ![]() for (NVOP).
for (NVOP).
4. Unified Duality
On the lines of Cambini and Carosi [16] , we associate with our primal problem (NVOP), the following unified dual problem (NVUD).
(NVUD) K-maximize ![]()
subject to ![]() (18)
(18)
![]() (19)
(19)
where![]() ,
, ![]() ,
, ![]() ,
, ![]() and
and ![]() is a 0 - 1 parameter.
is a 0 - 1 parameter.
Note that Wolfe dual and Mond-Weir dual can be obtained from (NVUD) on taking ![]() and
and ![]() respectively.
respectively.
Definition 4.1. Given the problem (NVOP) and given a vector ![]() we define the following Lagrange function:
we define the following Lagrange function:
![]() .
.
Theorem 4.1. (Weak Duality) Let x be feasible for (NVOP) and ![]() be feasible for (NVUD). If f is K-nonsmooth
be feasible for (NVUD). If f is K-nonsmooth ![]() -convex of order k with respect to
-convex of order k with respect to ![]() at y on
at y on ![]() and g is Q-nonsmooth
and g is Q-nonsmooth ![]() -convex of order k with respect to the same
-convex of order k with respect to the same ![]() at y on
at y on![]() , with
, with ![]() and
and
![]() , (20)
, (20)
then,
![]() .
.
Proof: Assume on the contrary that
![]() . (21)
. (21)
Since ![]() is feasible for (NVUD), therefore by (2), there exist
is feasible for (NVUD), therefore by (2), there exist ![]() and
and ![]() such that
such that
![]() . (22)
. (22)
Since f is K-nonsmooth ![]() -convex of order k with respect to
-convex of order k with respect to ![]() at y on
at y on![]() , we have
, we have
![]() (23)
(23)
Adding (21) and (23), we obtain
![]() .
.
As![]() , we get
, we get
![]() . (24)
. (24)
Also, since g is Q-nonsmooth ![]() -convex of order k with respect to
-convex of order k with respect to ![]() at y on
at y on ![]() and
and![]() , we have
, we have
![]() . (25)
. (25)
Adding (24) and (25), we get
![]()
or,
![]()
Using sublinearity of F under the assumption that ![]() and
and![]() , together with (22), (1) and (20), we obtain
, together with (22), (1) and (20), we obtain
![]() .
.
As ![]() and
and![]() , so that
, so that ![]() and we have
and we have![]() .
.
This contradicts the feasibility of![]() , hence the result.
, hence the result.
Theorem 4.2. (Weak Duality) Let x be feasible for (NVOP) and ![]() be feasible for (NVUD) with
be feasible for (NVUD) with ![]() and
and![]() . Suppose the following conditions hold:
. Suppose the following conditions hold:
(i) If ![]() is K-nonsmooth
is K-nonsmooth ![]() -pseudoconvex type II of order k with respect to
-pseudoconvex type II of order k with respect to ![]() at y on
at y on![]() , and
, and
(ii) If![]() , f is K-nonsmooth
, f is K-nonsmooth ![]() -pseudoconvex type II of order k with respect to
-pseudoconvex type II of order k with respect to ![]() at y on
at y on ![]() and g is Q-nonsmooth
and g is Q-nonsmooth ![]() -quasiconvex type I of order k with respect to
-quasiconvex type I of order k with respect to ![]() at y on
at y on![]() .
.
Then, we have
![]() .
.
Proof: Case (i): Let ![]() and on the contrary assume that,
and on the contrary assume that,
![]() . (26)
. (26)
Since x is feasible for (NVOP) and![]() , therefore
, therefore![]() . Further,
. Further, ![]() so that
so that
![]() . (27)
. (27)
Adding (26) and (27), we get
![]() .
.
That is,
![]() .
.
As ![]() is K-nonsmooth
is K-nonsmooth ![]() -pseudoconvex type II of order k with respect to
-pseudoconvex type II of order k with respect to![]() , we have for all
, we have for all ![]()
![]() .
.
Since, ![]() , we get
, we get
![]() ,
,
or
![]() ,
,
so that
![]() . (28)
. (28)
Now, since ![]() is feasible for (NVUD),
is feasible for (NVUD),
![]()
Therefore, there exists ![]() such that
such that![]() . Substituting in (28) and then using (1), we get
. Substituting in (28) and then using (1), we get
![]() ,
,
which is a contradiction, as ![]() and norm is a non-negative function.
and norm is a non-negative function.
Case (ii): Let![]() , then we have to prove that
, then we have to prove that
![]() .
.
Let if possible,
![]() .
.
Since f is K-nonsmooth ![]() -pseudoconvex type II of order k with respect to
-pseudoconvex type II of order k with respect to ![]() at y on
at y on![]() , we have
, we have
![]() .
.
As![]() , we get
, we get
![]() . (29)
. (29)
Since x is feasible for (NVOP) and ![]() is feasible for (NVUD), we have
is feasible for (NVUD), we have
![]() . (30)
. (30)
If![]() , (30) implies
, (30) implies![]() .
.
As g is Q-nonsmooth ![]() -quasiconvex type I of order k with respect to
-quasiconvex type I of order k with respect to ![]() at y on
at y on![]() , we get
, we get
![]() .
.
Since![]() , we have
, we have
![]() . (31)
. (31)
If![]() , then also (31) holds.
, then also (31) holds.
Since ![]() is feasible for (NVUD), by Remark 3.1, there exist
is feasible for (NVUD), by Remark 3.1, there exist ![]() and
and ![]() such that (22) holds.
such that (22) holds.
Adding (29) and (31), we get
![]() ,
,
or
![]() .
.
Using sublinearity of F with the fact that ![]() and
and ![]() and then using (22) and (1), we obtain
and then using (22) and (1), we obtain
![]() .
.
This contradicts the assumption that![]() , hence the result.
, hence the result.
Theorem 4.3. (Strong Duality) Let ![]() be a weak minimizer of order k with respect to
be a weak minimizer of order k with respect to ![]() for (NVOP) with
for (NVOP) with![]() , at which Slater-type cone constraint qualification holds. Then there exist
, at which Slater-type cone constraint qualification holds. Then there exist ![]() such that
such that ![]() is feasible for (NVUD). Further, if the conditions of Weak Duality Theorem 4.1 (Theorem 4.2) hold for all feasible x for (NVOP) and all feasible
is feasible for (NVUD). Further, if the conditions of Weak Duality Theorem 4.1 (Theorem 4.2) hold for all feasible x for (NVOP) and all feasible ![]() for (NVUD), then
for (NVUD), then ![]() is a weak maximizer of order k with respect to
is a weak maximizer of order k with respect to ![]() for (NVUD).
for (NVUD).
Proof: As ![]() is a weak minimizer of order k with respect to
is a weak minimizer of order k with respect to ![]() for (NVOP), by Theorem 3.2 there exist
for (NVOP), by Theorem 3.2 there exist ![]() such that
such that
![]() , (32)
, (32)
![]() . (33)
. (33)
Since![]() , Equations (32) and (33) can be written as
, Equations (32) and (33) can be written as
![]() ,
,
![]() .
.
Thus, ![]() is a feasible solution for (NVUD). Further, if
is a feasible solution for (NVUD). Further, if ![]() is not a weak maximizer of order k with respect to
is not a weak maximizer of order k with respect to ![]() for (NVUD), then for any
for (NVUD), then for any![]() , there exists a feasible solution
, there exists a feasible solution ![]() of (NVUD) such that
of (NVUD) such that
![]()
or,
![]()
Since, ![]() , so that we have
, so that we have
![]()
which contradicts Theorem 4.1 (Theorem 4.2). Hence ![]() is a weak maximizer of order k with respect to
is a weak maximizer of order k with respect to ![]() for (NVUD).
for (NVUD).
5. Conclusion
In this paper, we introduced the concept of a higher-order (weak) minimizer for a nonsmooth vector optimization problem over cones. Furthermore, to study the new solution concept, we defined new generalized classes of cone-nonsmooth (F, ρ)-convex functions and established several sufficient optimality and duality results using these classes. The results obtained in this paper will be helpful in studying the stability and convergence analysis of iterative procedures for various optimization problems.
NOTES
*Corresponding author.