Impact of Monthly Curve Number on Daily Runoff Estimation for Ozat Catchment in India ()
1. Introduction
The Natural Resources Conservation Service (NRCS) curve number (CN) procedure is widely used to estimate runoff resulting from rainfall. The primary reason for its wide applicability and acceptability lies in the fact that it accounts for major runoff-generating watershed characteristics, namely, soil type, land use/treatment, surface condition and antecedent moisture condition [1] -[3] . In contrast, the main weaknesses reported in the literature are that the SCS-CN method does not consider the impact of rainfall intensity; it does not address the effects of spatial scale. It is highly sensitive to changes in values of its single parameter CN, and it is ambiguous considering the effect of antecedent moisture conditions [4] - [6] . Nevertheless, the model development has made much progress in last three decades; a need of further improvements has always been experienced to satisfy unresolved challenges.
After the critical examination of the methodology, the SCS-CN method has gained much attention with respect to its modification and investigation. Subsequent studies (e.g. [7] - [10] ) examine the accuracy of the curve number method and identify specific weaknesses and limitations that are not widely recognized and that are rarely noted in textbooks. Recent modifications in determination of CN are reported by slope adjustment procedure [11] , two-CN system approach [12] and composite CN-generation [13] . The SCS-CN model implementing with these modifications would have a better simulation performance than the existing original SCS-CN. In CN method, parameters which influence the seasonal variation on predicting runoff have not been incorporated and hence they ignore the impact of seasonal and monthly variation. Although the CN method is well documented and widely used, as [14] pointed out, a need to use the method as a guideline and to interpret inputs on a more local and regional level combined with seasonal variation was essential. Runoff simulation with annually consistent parameters has limited application because watershed response varies remarkably from season to season. The seasonal tank model developed by [15] showed better performance compared with the non-seasonal tank mo- del because it can successfully simulate runoff with little error. CN on monthly basis, therefore, may also result in more accurate runoff estimation and improve the CN performance. The investigation reported in this paper is motivated by the need to evaluate the impact of monthly variation on the CN and its influence on runoff estimation for Ozat catchment.
The objectives of this study were 1) to assess the applicability of CNs determination procedures including the median, geometric mean [16] and standard asymptotic fit [17] in estimating runoff; 2) to evaluate the impact of the performance of monthly CN in prediction of runoff volume for Ozat watershed.
2. Materials and Methodology
2.1. Study Ares and Data Collection
Ozat is a river flowing in western India in Gujarat state whose origin is near Visavadar and meets in Arebian Sea. Ozat catchment considered in this study geographically locates within the latitudes 21˚19'N to 21˚33'N and the longitudes 70˚39'E to 70˚56'E respectively as can be seen from toposheet no 41 K (
10-11-14
and 15) of scale 1:50000. The gauge discharge site is located near Khambhaliya village at bridge of Junagadh to Visavadar Road
33 km
away from Junagadh. Information about soil and land use have been gathered from maps of National Bureau of Soil Survey and Land use Planning (ICAR) (1994). Study area (sub-watershed) has been delineated from Survey of India (SOI) topographic sheet using AutoCAD (2010) Software in Figure 1. The major portion of the precipitation occurs during the four months of June to September by south-west monsoon. The area is situated in semi-arid region with average annual rainfall of the area is
786 mm
(1980-2010), mean maximum temperature 33.34˚C and mean minimum temperature 24.30˚C. The total geographical area
358.8357 km
2 comprises of about 20.08% (
72.0542 km
2) grass and open scrub land and remaining 79.92% area under arable land irrigated (
286.7815 km
2). The major crops grown in the catchment are Ground nut, wheat and Cotton.
The hydrological data daily rainfall (mm) and runoff (m3/s) (1980 to 2010) and meteorological data daily maximum and minimum temperatures of Ozat catchment were collected from the State Water Data Centre, Gandhinagar. The information related to watershed characteristics, namely, physiography, number of streams of different orders, their length, slope and area contributing runoff to these streams were obtained from the topographic maps of the watershed.
Periodic insufficient rainfall pattern, limited water storage capacity of aquifer and natural water conservation are vital issues for this region. Water availability is a critical factor in this area and therefore accurate estimation of runoff is needed for water resources management, crop water use, farm irrigation scheduling, and environmental assessment.
![]()
Figure 1. Digitized 6th order drainage network map of Ozat catchment.
2.2. SCS-CN Method
One of the most commonly used methods to estimate the volume of surface runoff for a given rainfall event is the (SCS-CN) method [18] , which has been now renamed as (NRCS-CN) method. The SCS-CN method is based on the principle of the water balance and two fundamental hypotheses. The first hypothesis states that the ratio of direct runoff to potential maximum runoff is equal to the ratio of infiltration to potential maximum retention. The second hypothesis states that the initial abstraction is proportional to the potential maximum retention. The water balance equation and the two hypotheses are expressed mathematically respectively, as:
 (1)
(1)
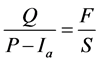 (2)
(2)
 (3)
(3)
where P is the total precipitation (mm), Ia is the initial abstraction before runoff (mm), F is the cumulative infiltration after runoff begins (mm), Q is direct runoff (mm), S is the potential maximum retention (mm), and λ is the initial abstraction (ratio) coefficient.
Small amount of rainfall events result in even smaller changes in runoff that can sometimes be difficult to discern in the discharge time series. To minimize uncertainty in the determination of the storm event discharge, storms events with P ≥
5 mm
have been considered to determine CN values in calibration period for this study. In validation period all events have been considered to measure performance of different procedures.
λ = 0.2 was assumed in original SCS-CN model. But, this assumption has often been questioned for its rationality and applicability, invoking a critical examination of the Ia-S relationship for practical applications [19] . A study using rainfall and runoff data from 307 US catchments or plots found that a value of λ = 0.05 would fit the data much better [20] . [21] found that the prediction accuracy for λ = 0.05 was greater than that for λ = 0.2 using SCS-CN method to simulate plot runoff of 757 rainfall events in Zizhou and Xifeng cities located in the Loess Plateau of China. Similar results have been obtained from plots or watersheds in USA [22] , semi-arid tropical highlands of Northern Ethiopia [23] and the Three Gorges area of China [24] . The assumption λ = 0.20 has been recently considered unusually high and recent studies [25] - [27] suggested the use of λ = 0.05. In the present study performance of all the methods were compared and tested with λ = 0.05, λ = 0.1 and λ =
0.2 in
validation.
The general runoff equation combination of Equation (1) and Equation (2) is shown in Equation (4):
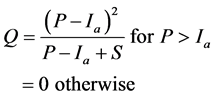 (4)
(4)
The potential maximum retention S (mm) can vary in the range of 0 ≤ S ≤ ∞, and it directly linked to CN. Parameter S is mapped to the CN using Equation (4) as:
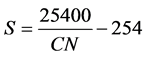 (5)
(5)
The CN depends on land use, hydrologic soil group, hydrologic condition, antecedent moisture condition (AMC) and it can vary from 0 to 100. Three AMCs were defined as dry (lower limit of moisture or upper limit of S), moderate (normal or average soil moisture condition), and wet (upper limit of moisture or lower limit of S), and denoted as AMC I, AMC II, and AMC III, respectively [28] . Higher amount of antecedent moisture and CN value would indicate the high runoff and vice versa, therefore, median CN computed from array of CN values and was commonly adopted for the catchment [29] .
Normally variations in storm characteristics and surface conditions can responsible for variation in CN between events. Possible sources of CN variability may be the effect of the temporal and spatial variability of storm and watershed properties, the quality of the measured data, and the effect of antecedent rainfall and associated soil moisture. [30] [31] also noted that the variation of CN value, according to AMC category alone, cannot justify the observed CN values variability in every case. Much of the variability in CN has been attributed to antecedent runoff content (ARC) such that soils that are wetter have a higher curve number, creating more runoff for a given amount of precipitation, than soils that are drier [32] [33] . Many researchers have demonstrated from rainfall and runoff data that its key parameter CN has variable components and is not a constant for a watershed [34] , and varies with rainfall. A parameter that exhibits seasonal variation on forecasting runoff volume has not been incorporated in the CN method and as a result ignores the impact of seasonal and monthly variation on evaporation, transpiration and interception. Therefore, monthly CN may play significant role in runoff estimation. A previous study [35] analyses the Variability of annual and seasonal curve number in Bamhani, Manot, Mohgaon and Shakkar watersheds of Narmada basin. They concluded that monthly CN indicates a homogeneous pattern of variation in all the four watersheds in the basin. Based on this previous work, we evaluated the performance of the median, geometric mean, and standard asymptotic fit procedures using monthly CN.
2.3. Curve Number Estimation
The CN values corresponding to the catchment soil types, land cover and land management conditions can be selected from the NEH-4 tables. The CN value of AMC II (CNII) was provided by the SCS-CN manual and the CN value of AMC I (CNI) and CN value of AMC III (CNIII) can be calculated by applying the [36] equations. CNI, CNII and CNIII values for Ozat catchment were computed 64.46, 81.20 and 90.85 respectively based on land used, soil characteristics and previous 5-day rainfall of the catchment.
In this study CNs were determined by three different methods using gauged rainfall and runoff. These methods include the median, geometric mean, and standard asymptotic fit. When rainfall-runoff data are available for a watershed, P and Q pairs are used directly to determine the potential retention S characterizing the watershed [37] as:
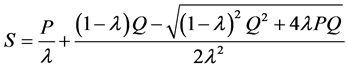 (6)
(6)
CN value can be directly calculated from rainfall-runoff data by substituting value of S in Equation (5) and rearranging it as:
 (7)
(7)
The median CN was computed by finding the median of the CNs of selected events from the calibration period (1980-1994). The CNs for events were computed using Equation (6) and Equation (7). The median CN as calculated from rainfall and runoff depths associated with the daily runoff events appears to have been the source of the original handbook table values. This procedure has the benefits of simplicity, precedent, and consistency with existing tables. However, it requires long records (one observation per year) and is incapable of capturing short term or transient effects, such as a fire or changes in agronomic practices [38] .
The geometric mean has been used to determine a watershed CN if the values calculated from rainfall and runoff measured for each event are log normally distributed [39] . Yet, no one seems to have established the log- normality of CN distributions. The major strength of the geometric mean is quantification of uncertainty with the standard deviation and confidence intervals. The normal distribution describes many random processes but it generally does not provide satisfactory fit for flood discharge and other hydrologic data. Though, the normal distribution is not well suited to hydrologic data, the related distribution; the lognormal distribution works reasonably well [40] . The geometric mean is obtained by finding the arithmetic mean of the series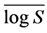 ; and then estimating the geometric mean maximum potential retention
; and then estimating the geometric mean maximum potential retention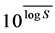 . The CN is then computed using Equation (8):
. The CN is then computed using Equation (8):
 (8)
(8)
where α =
254 mm
(
10 in
).
In standard asymptotic fit method (AFM), P and Q data are re-aligned on a rank-order basis, creating a new set of P:Q pairs (ordered P:Q data). This is done by rank ordering the rainfalls and runoff separately, and reassembling them as rank-ordered pairs. The Standard response was observed in Ozat catchment and to be described by the following:
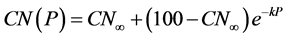 (9)
(9)
Equation (9) has the algebraic structure of the
Horton
infiltration equation. In the standard response, the CN as a function of rainfall P (CN[P]) decreases to an asymptotic constant CN∞ with k (the fitting coefficient or rate constant in the units of 1/P) that describes the CN approach to the asymptotic constant CN∞. Optimized values of CN∞ and k are obtained by fitting Equation (9) using least-squares procedure. The recent report to NRCS [41] recommends this procedure as the preferred technique for CN parameterization.
2.4. Monthly Curve Number
The mean monthly CNs of fifteen years period (1980-1994) were calculated using median method and geometric mean method. The highest values of CN were recorded in September month while the lowest values were recorded in the month of October. In (AFM) method, month wise optimized values of parameters CN∞ and k were computed using ordered P:Q data. CNs values were then determined by incorporating mean monthly rainfall amount of calibration period (1980-1994), CN∞ and k in Equation (9). Variations in CN with rainfall P for each month of monsoon season are presented in Figures 2-6 with parameters CN∞ and k values. Table 1 presents estimated monthly CN values by all three procedures with mean monthly rainfall. Month wise optimal values of parameters CN∞ and k during monsoon season are also presented in Table 1 for Ozat catchment.
In stream flow separation, the most frequently used methods are filtering separation method and statistical method (Frequency-Duration analysis). In filtering separation method, base flow separates from the stream flow time series data by processing or filtering procedure. Although these methods don’t have any physical basis it aims at generating an objective, repeatable and easily automated index that can be related to the base flow response of the catchment [42] . In this study the [43] filtering method is used to separate base flow from stream flow.
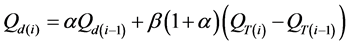 (10)
(10)
where,
Qd = direct flow part of the stream flow which is subjected to Qd ≥ 0 for the time i in days;
QT = total flow (i.e. base flow + direct flow);
α = a coefficient with value 0.925;
β = a coefficient with value 0.5.
3. Statistical Criteria
In this study, the performance of three CN determination procedures, viz, the median, geometric mean and standard asymptotic fit with standard CN and monthly CN are evaluated using two popular statistical criteria refined Willmott’s index (dr) [44] (Dimensionless statistic) and mean absolute error (MAE) (error index statistic). Dimensionless techniques provide a relative model evaluation assessment, and error indices quantify the deviation
![]()
Table 1. Month wise CN, CN∞ and K for different procedures.
![]()
Figure 2. Variations of CN with rainfall in the month of
June
for Ozat catchment.
![]()
Figure 3. Variations of CN with rainfall in the month of July for Ozat catchment.
![]()
Figure 4. Variations of CN with rainfall in the month of August for Ozat catchment.
![]()
Figure 5. Variations of CN with rainfall in the month of September for Ozat catchment.
![]()
Figure 6. Variations of CN with rainfall in the month of October for Ozat catchment.
in the units of the data of interest. These statistical criteria are used to measure the agreement between predicted and observed values of event runoff in validation period (1995-2010). To check precision and correctness of the methods, (dr) is applied. The
MAE
does not tell about degree of error but it is used for the quantitative analysis of residuals.
The dr is applied to quantify the degree to which values of observed runoff are captured by the models. The range of dr is from −1.0 to 1.0. A dr of 1.0 indicates perfect agreement between model and observation, and a dr of −1.0 indicates either lack of agreement between the model and observation or insufficient variation in observations to adequately test the model.
MAE
is error measure used to represent the average difference between model predicted and observed values. It is important to include absolute error measures
MAE
in a model evaluation because it provides an estimate of model error in the units of the variable. The MAE provides a more robust measure of average model error than the root mean square error (RMSE), since it is not influenced by extreme outliers [45] . A higher
MAE
value indicates poor model performance and vice versa.
MAE
= 0 indicates a perfect fit.
MAE
is the most natural and unambiguous measure of average error magnitude.
All the three procedures with standard CN and monthly CN values, considered for the present study, have been applied to estimate runoff for the Ozat catchment. The resulting values of dr, and MAE are presented in Table 2.
![]()
Table 2. Performance of different procedures in validation.
4. Results and Discussion
The median, geometric mean and standard asymptotic fit procedures are applied with standard CN and monthly CN on the data set of Ozat catchment. The data set of 15 years (1980-1994) was used to determine standard CN and monthly CN for each procedure and the data set of 16 years (1995-2010) was used for validation. The results of the performances of these methods are presented in Table 2. Performances of these methods on monthly time scale in validation period are shown in Figures 7-9.
It is evident from Table 1 that estimated CN values have direct relationship with λ. Median CNs are found in range from 43.82 to 88.65, geometric CNs in range from 48.25 to 85.41 and AFM CNs in range from 51.45 to 98.95. Median and geometric mean procedures are estimated the highest CN values for λ =
0.20 in
the month of September and the lowest CN value for λ =
0.05 in
the month of October. Median procedure estimated higher CN values than geometric mean procedure except in October month. Sudden drop found in CNs values from September to October month in median and geometric mean procedures which may be due to very little rainfall in October month. More than 98% precipitation occurs from
June
to September in Ozat catchment. CNs values increased gradually with λ from
June
to October in AFM method. Optimized values of parameter CN∞ are increased while optimized values of parameter k are decreased with increment in λ. CN∞ values exhibited inverse relationship with k values. The highest value of CN∞ is estimated in September month within range of 64.09 to 72.19 while lowest value is found in the month of October within range of 11.59 to 15.42. The values of k decrease from 0.21 to 0.01 with increment in the λ from 0.05 to 0.20, it is also evident that a value of k is the lowest in the month of October.
The AFM procedure is provided comparatively more realistic results with dr = 0.49 and
MAE
=
1.13 mm
for λ = 0.20. As compare to AFM method, other two methods are shown poor performance in goodness of fit criteria and produced the results with marginally larger errors. Substantial improvement in error estimate is noticed while using monthly CN values replacing standard CN values. For λ = 0.05, all three methods had a good performance in predicting the daily runoff with monthly CN values for the study area. These results are in good agreement to the previous studies.
5. Summary and Conclusions
The median, geometric mean and asymptotic fit procedures for CN determination are applied and evaluated with standard CN values and monthly CN values to estimate runoff for Ozat catchment of India.
The following conclusions can be drawn from this study:
1) The performance of the SCS-CN method is improved on application of monthly CN.
2) The CN values increase with increment in λ from 0.05 to 0.20.
3) The CN values computed from median procedure are higher than CN values computed from geometric mean procedure.
4) All the methods perform well with λ = 0.05 for Ozat catchment.
![]()
Figure 7. Performance of median CN and median monthly CN on monthly time scale in validation.
![]()
Figure 8. Performance of geometric mean CN and geometric mean monthly CN on monthly time scale in validation.
![]()
Figure 9. Performance of
AFM
CN
and AFM monthly CN on monthly time scale in validation.
5) The highest CN values are found in the month of September and the lowest CN values are found in the month of October for median and geometric mean methods.
6) Asymptotic CN parameters (CN∞) increase with λ and attain the highest value in September.
7) Inverse relationship is observed between λ and fitting parameter k.
8) The lowest values of parameters CN∞ and k are found in October.
Considering above all the results, we conclude that the relatively best performance is observed by the AFM method with higher dr values and lower
MAE
values. This study shows that the predictive capability of CN determination methods can be improved by the use of monthly CN values replacing standard CN values for the Ozat catchment.
Acknowledgements
The authors express sincere thanks to State Water Data Centre, Gandhinagar, for providing daily rainfall and runoff data of Khambhaliya Gauge Discharge Site and Divisional Office Junagadh (Irrigation Department), Gujarat for supplying us different maps of the study area.