Identification and Estimation of Gaussian Affine Term Structure Models with Regime Switching ()
1. Introduction
After [2] proposed the single factor Gaussian affine term structure model. The class of Gaussian affine term structure models (GDTSMs) has been generalized and developed by, [3] [4] , and [5] and has become the basic workhorse in macroeconomics and finance for purposes of using a no-arbitrage framework for studying the rela- tions between yields on assets of different maturities. [4] and [5] find the Gaussian form of three-factor affine term structure model describes US treasury yields better than other forms. However, there is an extensive em- pirical literature on bond yields (particularly short-term rates) that suggests that “switching-regime” models de- scribe the historical interest rate data better than single-regime models (see, for example, [1] [6] and [7] ).
[1] develop a discrete-time multi-factor DTSM with the following features: 1) within each regime the short-term interest rate follows a three-factor Gaussian model with state-dependent market prices of factor risks; 2) there are two regimes characterized by low (L) and high (H) volatility, and the transitions between these re- gimes under the historical measure P are governed by a Markov process with regime-shift probabilities that depend on the risk factors underlying changes in the shape of the yield curve; and 3) re- gime-shift risks are priced. This model yields exact closed-form solutions for bond prices, and an analytic re- presentation of the likelihood function that they use in their empirical analysis of US. Treasury zero-coupon bond yields. Expected excess returns are decomposed into two components, which are associated with re- gime-shift and factor risks, respectively.
that depend on the risk factors underlying changes in the shape of the yield curve; and 3) re- gime-shift risks are priced. This model yields exact closed-form solutions for bond prices, and an analytic re- presentation of the likelihood function that they use in their empirical analysis of US. Treasury zero-coupon bond yields. Expected excess returns are decomposed into two components, which are associated with re- gime-shift and factor risks, respectively.
But in the practical experience of those who have used DSY model are tremendous numerical challenges in estimating the necessary parameters from the data due to highly non-linear and badly behaved likelihood sur- faces. For example, [1] reported:
… Even with these normalizations/constraints, the resulting maximally flexible 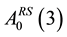 model (with restric- tions for analytical pricing) involves a high dimensional parameter space…
model (with restric- tions for analytical pricing) involves a high dimensional parameter space…
Another problem with DSY model is its identification. We find that DSY model parameters are universally unidentified. If there are some parameters in the model that are unidentified, then it will be wrong to make con- clusions from its parameters’ estimate, let us say about how regime-shift risks are priced.
This paper proposes solution to them and other problems with regime-switching affine term structure model of [1] based on what we will refer to as their reduced-form representation. For a popular class of re- gime-switching Gaussian affine term structure models―namely, those for which the model is claimed to price exactly a subset of 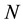 linear combinations of observed yields, where
linear combinations of observed yields, where 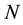 is the number of unobserved pricing factors―this reduced form is a restricted regime-switching multivariate linear regression in the observed set of yields.
is the number of unobserved pricing factors―this reduced form is a restricted regime-switching multivariate linear regression in the observed set of yields.
One implication is that the parameters of these reduced-form representations contain all the observable impli- cations of [1] regime-switching Gaussian affine term structure model for the sample of observed data, and can therefore be used as a basis for assessing identification. If more than one value for the parameter vector of inter- est is associated with the same reduced-form parameter vector, then the model is unidentified at that point and there is no way to use the observed data to distinguish between the alternative possibilities. [8] has applied this idea to affine term structure models with single regime. In this paper, we use it to demonstrate that [1] is in fact unidentified, an observation that our paper is the first to point out. This issue of identification is one factor that contributes to the numerical difficulties for conventional methods.
A second and completely separate contribution of the paper is that we propose our canonical representation of GDTSMs, which is then used in double-regime environment as a new form of regime-switching GDTSMs. Us- ing this form of representation, it is possible for the parameters of interest to be inferred directly from estimates of the reduced-form parameters themselves. This is a very useful result because the latter are often simple re- gime-switching OLS coefficients. Although translating from reduced-form parameters into structural parameters involves a mix of analytical and numerical calculations, the numerical component is far simpler than that asso- ciated with the usual approach of trying to find the maximum of the likelihood surface directly as a function of the structural parameters.
There have been several other recent efforts to use new development in GDTSMs for multi-regime considera- tion. [9] developed a no-arbitrage representation of a dynamic Nelson-Siegel model of interest rates that gives a convenient representation of level, slope and curvature factors. For example, [10] presents an affine, arbi- trage-free, regime-switching dynamic Nelson-Siegel model of the term structure (Regime-Switching AFNS). We show that it is a special case of our new form of regime-switching GDTSMs.
The chief difference between this paper and other relevant papers is that they focus on how the re- gime-switching GDTSMs should be represented, whereas we also examine how the parameters of the regime- switching GDTSMs are to be estimated.
The rest of the paper is organized as follows. Section 2 describes [1] regime-switching Gaussian affine term structure model. Section 3 investigates the mapping from structural to reduced-form parameters. We establish that the canonical forms of [1] are universally unidentified and a subset of their parameterization is over identi- fied. In Section 4, we propose a new representation. We establish when this representation is just-identified and how the parameters are to be estimated. In Section 5, we examine Regime-Switching AFNS’s representation. We establish that it is the constrained special case of our representation. Section 6 concludes.
2. Regime-Switching Gaussian Affine Term Structure Model
In this section, we just briefly describe the model set by [1] . Given the time t + 1 regime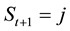 , under the risk-neutral measure (hereafter denoted by
, under the risk-neutral measure (hereafter denoted by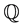 ), [1] assumes that the N-dimensional state (factor) vector Y fol- low the process
), [1] assumes that the N-dimensional state (factor) vector Y fol- low the process

where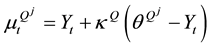 ,
, 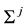 is a volatility matrix that is regime-dependent but not dependent on time, and
is a volatility matrix that is regime-dependent but not dependent on time, and 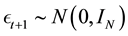 is standard normal.
is standard normal.
The regime-switching 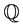 probabilities
probabilities  is state-independent.
is state-independent. 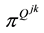 is the (j, k) element of
is the (j, k) element of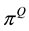 , denot- ing the
, denot- ing the ![]() probability of switching from regime
probability of switching from regime ![]() to regime
to regime![]() .
.
The continuously compounded yield on a one-period zero-coupon bond in regime j is assumed to be the affine function of![]() , that is,
, that is,![]() .
.
Letting ![]() denote the time t price for a zero-coupon bond with maturity of n periods, and
denote the time t price for a zero-coupon bond with maturity of n periods, and ![]() denote the price when the current regime is
denote the price when the current regime is![]() . Then, as is proved by [1] , we have,
. Then, as is proved by [1] , we have,
![]()
where,
![]()
![]()
with initial conditions:![]() . When n denotes maturities in months, the annualized yields are given by
. When n denotes maturities in months, the annualized yields are given by
![]() (1)
(1)
where![]() .
.
The market prices of factor (MPF) risks in regime j, ![]() , take a form of [5] ’s essentially affine, assuming that
, take a form of [5] ’s essentially affine, assuming that
![]() .
.
Given the time t + 1 regime![]() , under the historical measure (hereafter denoted by P), the N-dimen- sional state (factor) vector Y follows the process
, under the historical measure (hereafter denoted by P), the N-dimen- sional state (factor) vector Y follows the process
![]()
where![]() ,
, ![]() is a volatility matrix that is regime-dependent but not dependent on time,
is a volatility matrix that is regime-dependent but not dependent on time,
and ![]() is standard normal.
is standard normal.
The regime-switching P probabilities ![]() is state-dependent.
is state-dependent. ![]() is the (j, k) element of
is the (j, k) element of![]() , denoting the P probability of switching from regime
, denoting the P probability of switching from regime ![]() to regime
to regime![]() . For the two-regime case, they assume,
. For the two-regime case, they assume,
![]()
where j ≠ k. And then, the market price of regime-shift (MPRS) risk from ![]() to
to ![]() is as,
is as,
![]()
3. Identification of [1] ’s Model
[1] assumes that the yields on a collection of ![]() zero-coupon bonds are priced without error, and the yields on a collection of
zero-coupon bonds are priced without error, and the yields on a collection of ![]() zero-coupon bonds are priced with error. Let
zero-coupon bonds are priced with error. Let ![]() be the
be the ![]() vector of yields for the bonds priced exactly by the model and
vector of yields for the bonds priced exactly by the model and ![]() be the remaining
be the remaining ![]() vector of yields for the bonds priced with error.
vector of yields for the bonds priced with error.
[1] belongs to the class of state space models. Any regime-switching Gaussian affine term structure model in which exactly ![]() yields are assumed to be priced without error takes the form of a restricted regime-switching multivariate linear regression (LR). The mapping from the affine-pricing parameters to the LR parameters al- lows us to evaluate the identifiability of a given structure. If two different values for the structural parameters imply the identical reduced-form parameters, there is no way to use observable data to choose between the two. Based on this idea, [8] demonstrates that [4] [11] and [12] are in fact unidentified. We now explore the implica- tions of this fact for [1] described in the previous section.
yields are assumed to be priced without error takes the form of a restricted regime-switching multivariate linear regression (LR). The mapping from the affine-pricing parameters to the LR parameters al- lows us to evaluate the identifiability of a given structure. If two different values for the structural parameters imply the identical reduced-form parameters, there is no way to use observable data to choose between the two. Based on this idea, [8] demonstrates that [4] [11] and [12] are in fact unidentified. We now explore the implica- tions of this fact for [1] described in the previous section.
Given the time t regime![]() , according to (1), we have
, according to (1), we have
![]() (2)
(2)
where ![]() is a regime-dependent
is a regime-dependent ![]() vector,
vector, ![]() is a regime-independent
is a regime-independent ![]() factor loading matrix.
factor loading matrix.
Inverting (2) results in
![]()
Then,
![]()
where,
![]()
![]()
![]()
![]()
The remaining ![]() yields can be expressed as follows,
yields can be expressed as follows,
![]()
where,
![]()
![]()
![]()
The P-measure regime-switching probability ![]() can be transformed as follows,
can be transformed as follows,
![]()
where,
![]() ;
;
Letting ![]() be the vector of parameters relevant for re-
be the vector of parameters relevant for re-
gime-switching affine pricing and ![]() be the vector of parameters in the
be the vector of parameters in the
regime-switching multivariate linear regression model. ![]() is an implicit function of
is an implicit function of![]() . We know that
. We know that ![]() have one-to-one correspondence to observations and thus are identifiable. Therefore, we examine whe- ther the mapping from
have one-to-one correspondence to observations and thus are identifiable. Therefore, we examine whe- ther the mapping from ![]() to
to ![]() is one-to-one or not to determine the identifiability of
is one-to-one or not to determine the identifiability of![]() . If it is a multi-to-one mapping, then
. If it is a multi-to-one mapping, then ![]() is unidentified; if it is a one-to-one mapping, then
is unidentified; if it is a one-to-one mapping, then ![]() is just-identified; and if a one-to-multi mapping, then
is just-identified; and if a one-to-multi mapping, then ![]() is over identified.
is over identified.
However, which kind of mapping it may be is not inherent in the model but depends on the data structure used. For example, if the dimension of ![]() (that is M) increases (or decreases) by 1, then the number of parameters in
(that is M) increases (or decreases) by 1, then the number of parameters in ![]() of
of ![]() will increase (or decrease) by 1, and the number of parameters in
will increase (or decrease) by 1, and the number of parameters in ![]() will increase (or decrease) by
will increase (or decrease) by![]() . On the other side, all subsets of
. On the other side, all subsets of ![]() but
but ![]() remain the same size. Therefore, the number of
remain the same size. Therefore, the number of ![]() is crucial for the identification of
is crucial for the identification of![]() .
.
[1] estimates a two-regime, three-factor ![]() model. The vector
model. The vector ![]() includes the yields on bonds with maturities of 6, 24, and 120 months, and M = 1 with
includes the yields on bonds with maturities of 6, 24, and 120 months, and M = 1 with ![]() chosen to be the yield on the 60-month bond. The two regimes are denoted L and H, corresponding to “low” and “high” values of the diagonal entries of
chosen to be the yield on the 60-month bond. The two regimes are denoted L and H, corresponding to “low” and “high” values of the diagonal entries of![]() .
.
Firstly, let us look at the flexibility of [1] ’s empirical model. They set![]() ,
, ![]() and
and ![]() as free parameters
as free parameters
in their model. Consequently, ![]() as well as
as well as ![]() are derived parameters using equations
are derived parameters using equations ![]()
and![]() . Furthermore, they set
. Furthermore, they set ![]() to a lower triangular matrix which has 6 free parame-
to a lower triangular matrix which has 6 free parame-
ers, and ![]() to a form of
to a form of ![]() which has 5 free parameters. However, even though
which has 5 free parameters. However, even though ![]() is
is
unrestricted full matrix, ![]() only has 9 parameters which is less than the sum of the number of parameters contained in
only has 9 parameters which is less than the sum of the number of parameters contained in ![]() and
and![]() . In this case, there would be more than one set of
. In this case, there would be more than one set of ![]() and
and ![]() that fulfill the equa-
that fulfill the equa-
tion ![]() for some real
for some real![]() , making parameters
, making parameters ![]() and
and ![]() unidentified. On the other hand, if
unidentified. On the other hand, if
![]() is determined by fitting the P distribution of
is determined by fitting the P distribution of![]() , then
, then ![]() only has as many free parameters as
only has as many free parameters as![]() , therefore making
, therefore making ![]() an over-identified matrix. In this case, the model would be not so flexible.
an over-identified matrix. In this case, the model would be not so flexible.
Secondly, let us look at the total number of parameters for both models. Table 1 lists the number of free pa- rameters contained in ![]() which is 49. Besides, they fix some subsets of
which is 49. Besides, they fix some subsets of ![]() a priori, that is,
a priori, that is,
![]() ;
;![]() ;
; ![]() and
and![]() . These constraints re-
. These constraints re-
duce the total number of free parameters in ![]() to 41. Table 2 lists the number of free parameters contained in
to 41. Table 2 lists the number of free parameters contained in ![]() which is 34. Therefore, the only kind of mapping from
which is 34. Therefore, the only kind of mapping from ![]() to
to ![]() is multi-to-one, and there must be some parameters in
is multi-to-one, and there must be some parameters in ![]() which are unidentified.
which are unidentified.
4. A New Representation and Its Estimation
Due to the problems with identifiability of [1] parameters, we develop our “HW” canonical representation of re- gime-switching GDTSMs. Here, we use “HW” to represent [8] , because they first propose this normalization for three-factor GDTSMs. However, they do not further examine this form of normalization.
In [8] , they have proposed that for any 3 × 3 real-valued matrix:
![]()
there exist ![]() that makes
that makes![]() , where
, where ![]() takes following form:
takes following form:
![]()
with![]() .
.
Although, as is pointed out in [8] , this form cannot be extended to higher dimension, it has an advantage over others in that it can deal with the situation of ![]() having complex eigenvalues. This form is enough for us to
having complex eigenvalues. This form is enough for us to
![]()
Table 1. The number of free parameters in![]() .
.
![]()
Table 2. The number of free parameters in![]() .
.
study regime-switching three-factor GDTSMs. Next, we propose an alternative normalization in the following Theorem.
Theorem 1. Every three-factor canonical GDTSM is observationally equivalent to the three-factor canonical GDTSM with
![]() (3)
(3)
![]() (4)
(4)
![]() (5)
(5)
where, ![]() takes the following form:
takes the following form:
![]()
![]() is a 3 × 1 vector,
is a 3 × 1 vector, ![]() is a 3×3 factor loading matrix,
is a 3×3 factor loading matrix, ![]() represents
represents![]() ,
, ![]() is a scalar.
is a scalar.
Proof:
Assuming some three-factor canonical GDTSM takes the following form:
![]()
For ease of exposition, we assume we have found![]() , making
, making![]() , and
, and ![]() takes the form:
takes the form:
![]()
Then, letting![]() , where
, where![]() . We can regard
. We can regard ![]() as a new state
as a new state
factor, because the mapping from ![]() to
to ![]() is one-to-one. The
is one-to-one. The ![]() dynamic process of
dynamic process of ![]() can be obtained as follows,
can be obtained as follows,
![]()
where, ![]() which also takes the same form as
which also takes the same form as![]() , that is,
, that is,
![]()
Likewise, the ![]() dynamic process of
dynamic process of ![]() can be obtained as follows,
can be obtained as follows,
![]()
where, ![]() ,
,![]() . Both
. Both ![]() and
and ![]() are unrestricted vector and matrix be-
are unrestricted vector and matrix be-
cause we do not impose any restriction on either ![]() or
or![]() .
.
Finally, we can transform the short rate as an affine function of the new state variables as follows,
![]()
where, ![]() which is a scalar.
which is a scalar.
By Theorem 1, we will establish the reparametrization of [1] regime-switching three-factor GDTSM as fol- lows.
Given the time t regime![]() , under
, under![]() , we assume that the three-dimensional state vector
, we assume that the three-dimensional state vector ![]() follow the process,
follow the process,
![]()
where ![]() takes the form of
takes the form of![]() ,
, ![]() is a volatility matrix that is regime-dependent but not de-
is a volatility matrix that is regime-dependent but not de-
pendent on time, and ![]() is standard normal. Unlike [1] , we do not have to set the intercept term. In order to have closed-form solutions for zero-coupon bond prices, we still set
is standard normal. Unlike [1] , we do not have to set the intercept term. In order to have closed-form solutions for zero-coupon bond prices, we still set ![]() to be state-independent.
to be state-independent.
Like [1] , the regime-switching ![]() probabilities
probabilities ![]() is state-independent.
is state-independent. ![]() is the (j, k) element of
is the (j, k) element of![]() , denoting the
, denoting the ![]() probability of switching from regime
probability of switching from regime ![]() to regime
to regime![]() .
.
Unlike [1] , the continuously compounded yield on a one-period zero-coupon bond in regime j is assumed to
be a different affine function of![]() , that is,
, that is,![]() .
.
Then, given the time t regime![]() , the time-t price for a zero-coupon bond with maturity of n periods
, the time-t price for a zero-coupon bond with maturity of n periods ![]() is computed as follows,
is computed as follows,
![]()
where,
![]()
![]() .
.
with initial conditions:![]() . When
. When ![]() denotes maturities in months, the annualized yields are given by
denotes maturities in months, the annualized yields are given by
![]() (1)
(1)
where![]() .
.
Given the time t regime![]() , under
, under![]() ,
, ![]() follows the process
follows the process
![]()
where![]() ,
, ![]() and
and ![]() are state-dependent parameters.
are state-dependent parameters.
Like [1] , the regime-switching ![]() probabilities
probabilities ![]() is state-dependent. For the two-regime case, we still assume,
is state-dependent. For the two-regime case, we still assume,
![]()
And then, the market price of regime-shift (MPRS) risk from ![]() to
to ![]() is as,
is as,![]()
Like [1] , we could set the market prices of factor risks in regime j,![]() . However, we do
. However, we do
not set ![]() and
and ![]() to be free parameters. Instead, we set
to be free parameters. Instead, we set![]() ,
, ![]() and
and ![]() as free parameters in our mo-
as free parameters in our mo-
del. Consequently, ![]() as well as
as well as ![]() are derived parameters using equations
are derived parameters using equations ![]() and
and![]() .
.
A distinctive feature of this reparametrization is that, in estimation, there is an inherent separation between the parameters of the ![]() and
and ![]() distributions of
distributions of![]() . In contrast, when the risk factors are latent, estimates of the parameters governing the
. In contrast, when the risk factors are latent, estimates of the parameters governing the ![]() distribution necessarily depend on those of the
distribution necessarily depend on those of the ![]() distribution of the state, since the pricing model is required to invert the model for the fitted states (when N bonds are priced perfectly). We will formalize this “separation property” of our reparametrization in the following contents.
distribution of the state, since the pricing model is required to invert the model for the fitted states (when N bonds are priced perfectly). We will formalize this “separation property” of our reparametrization in the following contents.
As in [1] , we assume that the yields on a collection of three zero-coupon bonds are priced without error, and the yields on a collection of ![]() zero-coupon bonds are priced with error. In this data structure, we will prove that, for two-regime model, the sufficient condition of just-identification of our normalization is
zero-coupon bonds are priced with error. In this data structure, we will prove that, for two-regime model, the sufficient condition of just-identification of our normalization is![]() .
.
Let ![]() be the
be the ![]() vector of yields for the bonds priced exactly by the model and
vector of yields for the bonds priced exactly by the model and ![]() be the remaining
be the remaining ![]() vector of yields for the bonds priced with error.
vector of yields for the bonds priced with error.
Given the time t regime![]() , according to (1), we have
, according to (1), we have
![]() (2)
(2)
where ![]() is a regime-dependent
is a regime-dependent ![]() vector,
vector, ![]() is a regime-independent
is a regime-independent ![]() factor loading matrix.
factor loading matrix.
Inverting (2) results in
![]()
Then,
![]()
where,
![]()
![]() ,
,
![]() ,
,
![]() .
.
The remaining 2 yields can be expressed as follows,
![]()
where,
![]() ,
,
![]() ,
,
![]() .
.
The ![]() -measure regime-switching probability
-measure regime-switching probability ![]() can be transformed as follows,
can be transformed as follows,
![]()
where,
![]()
![]()
In summary, we can use the method proposed in [13] to estimate the parameters
![]() , then we can back out our state-space parameters
, then we can back out our state-space parameters
![]() =
= ![]() as follows.
as follows.
Step 1. The estimate of the 6 unknowns in ![]() is obtained by numerically solving the 6 equations in
is obtained by numerically solving the 6 equations in![]() .
.
Step 2. The estimate of ![]() is obtained analytically by the equation
is obtained analytically by the equation![]() , that is
, that is![]() .
.
Step 3. The estimate of the 4 unknowns in ![]() is obtained by numerically solving the 4 eq- uations in
is obtained by numerically solving the 4 eq- uations in
![]()
and,
![]()
Step 4. The estimate of ![]() is obtained analytically by the equation
is obtained analytically by the equation![]() , that is
, that is
![]() .
.
Step 5. The estimate of ![]() is obtained analytically by the equation
is obtained analytically by the equation![]() ,
,
that is![]() .
.
Step 6. The estimate of ![]() is obtained analytically by the equation
is obtained analytically by the equation![]() , that is
, that is![]() .
.
Step7. The estimate of ![]() is obtained analytically by the equation
is obtained analytically by the equation ![]() that
that
is![]() .
.
In every step, the solving processes can be invertible, so we can also obtain ![]() from
from![]() . That is the mapping relation between
. That is the mapping relation between ![]() and
and ![]() is one-to-one, and the parameters of our normalization are just- identified.
is one-to-one, and the parameters of our normalization are just- identified.
When M = 1, the situation is different. In Step 1, there are still 6 unknowns in![]() , while there are only 3 equ-
, while there are only 3 equ-
ations in![]() ; in Step 3, we still need estimate the 4 unknowns in
; in Step 3, we still need estimate the 4 unknowns in ![]() ,while there are
,while there are
only 2 equations in ![]() and
and![]() . The mapping from
. The mapping from ![]() to
to ![]() is mul-
is mul-
ti-to-one and so the parameters of our normalization are unidentified.
When![]() , we will see our state-space parameters
, we will see our state-space parameters ![]() to be over identified. In Step 1, there will be at least 3 × 3 = 9 equations, but we still need to estimate only 6 unknowns in
to be over identified. In Step 1, there will be at least 3 × 3 = 9 equations, but we still need to estimate only 6 unknowns in![]() . In Step 3, there will be at least 3
. In Step 3, there will be at least 3
× 2 = 6 equations in ![]() and
and![]() , but we there are still only 4 unknowns in
, but we there are still only 4 unknowns in
![]() . This means that the mapping from
. This means that the mapping from ![]() to
to ![]() is one-to-multi and so the parameters
is one-to-multi and so the parameters
of our normalization are over identified.
The next question is how to obtain the standard error for these state-space parameters![]() . [8] has proved that under the usual regularity conditions, we could use Delta Methods to obtain the asymptotic standard errors of the structural parameters.
. [8] has proved that under the usual regularity conditions, we could use Delta Methods to obtain the asymptotic standard errors of the structural parameters.
Within [1] ’s parametrization, the ![]() parameters control the cross-sectional relationship among the yields and the latent factors are fitted from observed yields, so the estimates of the parameters governing the
parameters control the cross-sectional relationship among the yields and the latent factors are fitted from observed yields, so the estimates of the parameters governing the ![]() dis- tribution will necessarily depend on those of the
dis- tribution will necessarily depend on those of the ![]() distribution of the state. On the other hand, [1] ’s parame- trization also makes the
distribution of the state. On the other hand, [1] ’s parame- trization also makes the ![]() parameters as derived parameters from
parameters as derived parameters from ![]() parameters. Therefore, we cannot back out
parameters. Therefore, we cannot back out ![]() parameters and
parameters and ![]() parameters separately in [1] ’s model, while our model’s parametrization makes this “separation property” possible.
parameters separately in [1] ’s model, while our model’s parametrization makes this “separation property” possible.
5. Regime-Switching Three-Factor Arbitrage-Free Nelson-Siegel Model.
In this section, we will show that the regime-switching extension on the AFNS model of [9] is a constrained spe- cial case of our representation.
By [9] , under![]() , the three-dimensional state vector
, the three-dimensional state vector ![]() follow the process,
follow the process,
![]() (6)
(6)
where ![]() is a volatility matrix and
is a volatility matrix and ![]() is standard normal. The short rate depends only on the first two latent pricing factors, that is,
is standard normal. The short rate depends only on the first two latent pricing factors, that is,
![]() (7)
(7)
First, we let ![]() to be a new state vector. Replacing
to be a new state vector. Replacing ![]() with
with ![]() in (6) and (7), we have,
in (6) and (7), we have,
![]() (8)
(8)
![]() (9)
(9)
where
![]() .
.
Second, let![]() , with
, with![]() . Premultiply both sides of (8) by
. Premultiply both sides of (8) by![]() , we have,
, we have,
![]() (10)
(10)
where![]() . Inserting
. Inserting ![]() into(7)produces
into(7)produces
![]() (11)
(11)
where![]() .
.
Comparing (10) with (3), we find that the regime-switching AFNS model is the constrained special case of
the our normalization with![]() ,
, ![]() ,
, ![]() ,
, ![]() and
and![]() .
.
Sometimes, we want to test if these constraints are valid. We could set regime-switching AFNS model as the null model and our representation as the alternative model, and then, under a desired statistical significance level, we compare likelihood ratio to the chi squared value with degrees of freedom equal to 5.
6. Conclusions
[1] ’s regime-switching three-factor affine term structure model, when we assume that the yields on a collection of three zero-coupon bonds are priced without error, is simply a restricted regime-switching linear regression. We use this correspondence to demonstrate that [1] ’s parameters are in fact universally unidentified and a subset of their parameterization is over identified. As a solution to the problem with the identifiability, we propose a canonical representation of GDTSMs based on [8] ’s proposal, which is then used in double-regime environment as a new form of regime-switching GDTSM. We also demonstrate that the parameters of our new form of re- gime-switching GDTSM are just-identified when the number of the pricing-with-error yields M equals 2. Our model’s parametrization has another advantage over [1] in that we can back out ![]() parameters and
parameters and ![]() para- meters separately and make the estimation of structural parameters easier. Finally, we show that regime- switching three-factor arbitrage-free dynamic Nelson-Siegel model is a restricted special case of our model.
para- meters separately and make the estimation of structural parameters easier. Finally, we show that regime- switching three-factor arbitrage-free dynamic Nelson-Siegel model is a restricted special case of our model.
Besides, due to the tremendous numerical challenges in estimating the necessary parameters, we hope that our method will help to make these models a more effective tool for research in better describing the historical in- terest rate data.
Acknowledgements
This work is supported by Research Innovation Foundation of Shanghai University of Finance and Economics under Grant No. CXJJ-2013-321. And I am especially grateful to Professor Hong Li for his support and encou- ragement. All errors are my own.