An Automatic Approach for Satisfying Dose-Volume Constraints in Linear Fluence Map Optimization for IMPT ()
Radiation oncologists use dose-volume constraints (DVCs) to prescribe and control the dose to the target and OARs. The DVC specifies what fraction of a structure is allowed to receive a radiation dose higher than the specified upper threshold value or lower than the specified lower threshold value. For example, according to the lung protocol at The University of Texas MD Anderson Cancer Center, the treatment planner may specify that “no more than 37% of the normal lung is allowed to receive 20 Gy or more” instead of imposing a strict upper dose limit of 20 Gy on the normal lung. Sometimes the clinical goal of achieving an effective dose for all targets while preserving the OARs cannot be met. In such cases, a compromise must be found and the DVCs relaxed. However, modifying DVCs is a highly complex problem, and finding the global optimal solution can be very difficult [2,3].
Linear programming (LP) is a powerful method for modeling FMO, but DVCs cannot be incorporated directly into the FMO model without introducing integer variables. Integer variables are needed because a DVC limits the dose applied for a certain number of voxels. Determining exactly how many of the voxels should meet DVCs is a difficult combinatorial problem that has multiple local optima and is nonconvex and nondeterministic polynomial time hard [4,5].
There are many formulations and solution methods for the FMO problem under DVCs. Ehrgott, Güler, Hamacher, and Shao [6] reviewed the mathematical optimization in intensity-modulated radiation therapy, including DVC-based models. One of the common nonlinear approaches minimizes the total weighted nonlinear function of the dose deviation violation [7,8]. Local search methods have been reported to solve these models, including gradient-based methods [8] and metaheuristics such as simulated annealing [9] and genetic algorithm [10].
Xing, Li, Donaldson, Le, and Boyer [11] defined a DVH score function, and developed an algorithm that performs a sequence of nonlinear optimizations which updated the optimization parameters to improve the score. Cho et al. [12] discussed two optimization techniques for intensity beam modulation with DVCs. The first method, cost function minimization, applies a volume-sensitive penalty function in which fast simulated annealing is used. In the second one, the convex projection method, the DVC is replaced by a limit on the integral dose.
Michalski, Xiao, Censor, and Galvin [13] formulated a DVC satisfaction search for the discretized radiation therapy model. The aperture-based approach with predefined segmental fields was used in inverse treatment planning, followed by an iterative algorithm of the simultaneous sub-gradient projections to obtain solutions.
Another model used to solve the FMO problem is the weighted least-squares model, which focuses on dosevolume-based weighted least-squares. These models are fast, but they only give an approximate solution. Although the DVC can be directly incorporated into the objective function, the objective function will no longer be convex and differentiable. Zhang and Merritt [3] presented a new least-squares model that has a monotonic and differentiable objective function. In their model, the greedy algorithm has been applied to approximately solve the optimization model faster than other existing algorithms.
Nonlinear methods may provide local optimal or suboptimal solutions once DVCs are incorporated [4,14]. However, there is not sufficient information about the optimality gap to allow us to understand the difference between these local solutions and a global optimal solution. Romeijn, Ahuja, Dempsey, Kumar, and Li [15] approximated any convex objective function by using a piecewise linear convex objective function that can be solved quickly and easily for a global optimal solution. They incorporated an approximation of DVCs by formulating conditional value-at-risk constraints on the differential dose-volume histogram (DVH). Langer and Leong [16] also formulated and solved the problem of optimizing the beam weights under DVCs using linear programming.
Romeijn, Ahuja, Dempsey, and Kumar [17] approximated the DVC by “mean-tail-dose”, which refers to the mean dose of either the hottest or coldest specified volume. An advantage of the mean-tail-dose approach is that the metrics can be formulated linearly. Also, the global optimum can be more easily achieved because the problem is convex; however, DVC cannot be replaced by a mean-tail-dose in the clinic.
In the work by Chen, Herman, and Censor [2], two existing approaches to satisfy DVCs were discussed: linear programming and ART3+, an adaptation of a projection method for solving feasible systems of linear inequalities. The two methods were compared in terms of their ability to find an optimal solution as well as their computational speed.
Mixed-integer programming (MIP) is another technique commonly used by researchers to model DVCs [18-24]. However, MIP models are too difficult to solve to be practically useful because of their nonconvex and nondeterministic polynomial time hard characteristics. Tuncel, Preciado, Rardin, Langer, and Richard [5] introduced a family of disjunctive valid inequalities to the MIP formulation of the FMO problem under DVCs. A heuristic algorithm based on the geometric distance sorting technique is proposed by Lan, Li, Ren, Zhang, and Min [21] for solving a Linear constrained, quadratic objective MIP formulation of the FMO with DVCs.
Preciado-Walters, Rardin, Langer, and Thai [22] formulated the FMO problem as an MIP model over a coupled pair of column generation processes. One of the processes makes intensity maps, and the other determines the protected area for organs under DVCs. Dink et al. [25,26] also incorporated DVCs into an MIP model: on the basis of work by Morrill, Lane, Wong, and Rosen [27].
Typically, the FMO problem that considers DVCs has multiple local optima and is non-deterministic polynomial time hard [4,5]. There is no guarantee that the gradient-based solution methods and metaheuristics proposed to solve non-LP formulations would allow us to find a global optimal solution. Those methods usually find local optimal and/or suboptimal solutions [5]. In contrast, MIP models can guarantee global optimality. But solving the MIP models with DVCs can take such a long time that they may not be useful in clinical practice [14].
Multiobjective optimization is often used to optimize fluence maps, although choosing the appropriate values for the weight parameters and hotand cold-spot control parameters is not straightforward and requires a trial-and-error approach. In this paper, we developed a Linear-based heuristic algorithm to satisfy DVCs that eliminates the manual selection of those parameters. This algorithm begins by setting loose boundaries for hotand cold-spot control parameters; then, after checking the dose-volume criteria, it gradually tightens the boundaries, if the DVC criteria are not satisfied. At the same time, our algorithm increases the objective function weight parameters for organs but does not satisfy their corresponding DVCs. Although this proposed method should work well for intensity-modulated radiation therapy, our method was developed specifically for IMPT. Proton therapy is increasingly being used to treat cancer patients in clinical practice. Thus, we tested our DVC satisfaction algorithm on IMPT cases.
2. Materials and Methods
2.1. Patient Data and Beam Configurations
We evaluated the relative performance of the optimization approaches by retrospectively creating treatment plans for one patient with prostate cancer and five patients with lung cancer who had previously undergone IMPT on a prospective institutional review board-approved protocol at MD Anderson Cancer Center in Houston, Texas. Two lateral beam fields were used for the prostate case while three beam fields were used for the lung cancer cases. The prescribed doses and beam configurations are listed in Table 1. For the patients with lung cancer, which are more complicated than the patient with prostate cancer, we used two methods of FMO (linear and nonlinear) to evaluate DVC satisfaction.
2.2. DVC
In this study, we used the same DVCs used in the original treatment protocols and adopted in the clinic. The following DVC protocols were used for the prostate cancer case: 1) rectum: V70 ≤ 25% (≤25% of the rectum is allowed to receive 70 Gy or more); 2) bladder V65 ≤ 25%; and 3) bladder V40 ≤ 50%. The DVCs and meandose constraints used in the lung irradiation case were as follows:
1) Planning target volume (PTV): ≥ 95% of the PTV volume receives ≥ 95% of the prescribed dose.
2) PTV: No more than 2 cm3 receives ≥ 120% of the prescribed dose (minor deviation) or no more than 2 cm3 receives ≥ 110% of the prescribed dose (no deviation).
3) Normal lung: V20 ≤ 37%.
4) Normal lung: Mean lung dose ≤ 20Gy relative biological effectiveness.
5) Heart: V45 ≤ 30%.
6) Heart: mean dose ≤ 35Gy relative biological effectiveness.
2.3. Linear FMO
The FMO model optimizes the amount of radiation that each beamlet delivers when the gantry is positioned at a given angle. The goal of this model is to find the optimal beamlet weights, assuming that a set of beam angles are given as input parameters. The objective function for this model can be either linear or nonlinear. We describe our model, which is based on the linear FMO model by Lim, Choi, and Mohan [28] in Section 2.4. Then, in Section 2.5, a nonlinear alternative FMO is presented. The input parameters for the linear FMO are shown in Table 2. A cold spot represents a portion of a structure that receives less than the desired radiation dose. A hot spot represents a portion of a structure that receives a dose higher than the desired upper boundary.
The voxels in the OARs are denoted by Sk to signify a collection of k OARs, and T represents the voxels in the PTV. Each voxel is represented by a three dimensional coordinate, (x,y,z). The dose contribution d(x,y,z,j) is calculated via an in-house-developed dose calculation engine [29], where d(x,y,z,j) denotes the dose contributed by the jth beamlet per unit weight, and is received by voxel (x,y,z). Given that the decision variable wj is the intensity of beamlet j, the total dose in voxel (x,y,z) can be calculated as 
The standard LP model to optimize the beamlet weights is constructed as follows. The objective function of the LP model has three terms that are associated with the target and OARs.
 where,
where,  for all (x,y,z). Note that for a vector x, 1-norm
for all (x,y,z). Note that for a vector x, 1-norm  is the sum of the ab-
is the sum of the ab-

Table 1. Dose and beam configurations.

Table 2. Input parameters for linear FMO.
solute values of the columns . The notation (.)+
. The notation (.)+
represents max{•,0}, DT and DS are doses to the target and OARs respectively, and eT and eS are the vectors of ones.
2.4. LP Heuristic Algorithm to Satisfy DVCs in Linear FMO
The linear FMO model [28] imposes strict hot spot control parameters on both the target and the OARs and strict cold spot control parameters on the target. This approach often helps satisfy the DVCs if the values are selected appropriately. The values of the parameters can sometimes be shown to be unnecessarily conservative, which compromises the quality of the treatment plan for other organs. Consequently, a tedious trial-and-error effort is made to find appropriate parameter values. To eliminate this trial-and-error approach, applying the techniques for controlling dose-volume histogram by Lim, Ferris, Shepard, Wright, and Earl [30], our algorithm starts by setting arbitrarily loose upper boundaries on these parameters; it then gradually tightens the boundaries and simultaneously increases the objective penalty coefficients through an iterative solution process. Following this iterative process, appropriate parameter values are determined, which results in an even trade-off between OAR sparing and target coverage. The algorithm stops when all of the DVCs are satisfied or when no more improvement can be made in the DVCs. The algorithm can be described as follows:
1) Initialize φ and λS for OARs, as well as ,
,  , θL, and θU for the target.
, θL, and θU for the target.
2) Solve the FMO model.
3) If all constraints are satisfied, stop; otherwise go to step 4.
4) Remove all OAR voxels that satisfy the DVCs from sets Sk and keep the remaining (or DVC-violating) voxels for the next iteration, if there are any violated DVCs for OARs.
5) Decrease the hot spot control parameter (φ) and increase the penalty coefficient for hot spots (λS) if any of the constraints of an OAR are not satisfied.
6) For violated DVCs of the target, increase the corresponding penalty coefficient ( and
and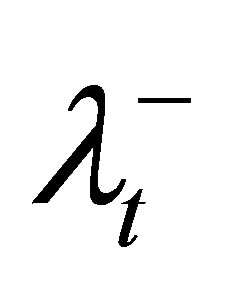 ), tighten the corresponding control parameter (increase θL or decrease θU), and then go to step 2.
), tighten the corresponding control parameter (increase θL or decrease θU), and then go to step 2.
2.5. Nonlinear FMO
This problem can also be modeled using the nonlinear (mostly quadratic) objective function. A quadratic model used to optimize the weights is constructed as follows:

Similar to the LP model, λ terms denote the penalty weights of the corresponding organs.  and
and  are the upper and lower prescribed dose levels for the tumor, respectively, and
are the upper and lower prescribed dose levels for the tumor, respectively, and  is the tolerance dose for the kth OAR.
is the tolerance dose for the kth OAR.
In order to take in to account the non-negativity of the beamlet intensities, the weight of beamlet j is denoted by the non-negative quantity . As a result, the constrained optimization problem with respect to weights is turned into an unconstrained one of optimizing the square root of the beamlet weights instead of optimizing the beamlet weight directly.
. As a result, the constrained optimization problem with respect to weights is turned into an unconstrained one of optimizing the square root of the beamlet weights instead of optimizing the beamlet weight directly.
The objective function penalizes quadratic integral dose violations to the target and the OARs. The model only includes OAR voxels receiving doses greater than their tolerance dose levels. The penalty weights and the prescribed and tolerance doses for the target and OARs can be altered by the treatment planner. The limited memory Broyden-Fletcher-Goldfarb-Shanno (L-BFGS) method is applied to solve this unconstrained optimization model [31,32].
3. Results
3.1. Prostate Cancer Case
We tested our LP heuristic algorithm on a prostate cancer case. Two major OARs were the rectum and bladder. Note that we normalized the prescribed dose on the PTV so that the value of 1 stands for the prescribed radiation dosage level on the tumor. The normalization was done for all the experiments in this paper. Typically, the values of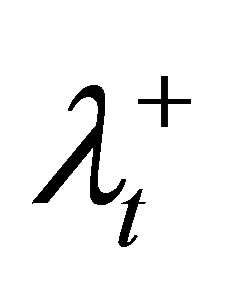 ,
,  , and λS are selected by the treatment planner. In our experiments, we started the algorithm by assigning equal weights to the PTV and OARs. The algorithm then adjusted these values in order to satisfy the DVCs.
, and λS are selected by the treatment planner. In our experiments, we started the algorithm by assigning equal weights to the PTV and OARs. The algorithm then adjusted these values in order to satisfy the DVCs.
For the prostate cancer case, all DVCs were satisfied by the algorithm at its initial iteration (which is the same as the linear FMO) and the algorithm was terminated. However, to assess the algorithm, we modified the DVCs to make them much harder to satisfy. Figure 1 shows how using the algorithm for organ sparing and to maintain the target dose coverage affected the DVH.
3.2. Lung Cancer Cases
3.2.1. Results for the LP Heuristic Approach
In this section, we applied our developed method to five cases of lung cancer. These cases were more complicated than the case of the patient with prostate cancer discussed in the previous section. Lung cancer cases include two of the most critical OARs: normal lung and heart. Table 3 presents the progression of the LP heuristic algorithm, from the initial iteration to the final one in terms of constraints satisfaction for all the lung cancer cases. The results of the first iteration showed unnecessarily conservative OAR sparing, whereas the PTV coverage was not enough to satisfy its corresponding DVCs.
For instance, DVC1 at the first iteration was not satisfied for Patient 1. As illustrated in Table 3, 80.7% of the PTV received a dose greater than or equal to 95% of the prescribed dose, which was not greater than or equal to the corresponding reference point (95%) and thus violated the reference criteria. On the other hand, for DVC3, 21.6% of the normal lung received a dose greater than or equal to 20 Gy at the first iteration, which was significantly less than the reference point (37%). However, at the final iteration of the LP heuristic for the same patient, 99.6% of the PTV received a dose greater than or equal to 95% of the prescribed dose, which satisfied the reference criteria for DVC1, and 29.7% of the normal lung received a dose greater than or equal to 20 Gy, which was still less than the reference point for DVC3 (37%).
Hence, in the last iteration, the LP heuristic found solutions that satisfied the constraints for all organs through an iterative process by automatically adjusting the optimization model parameter values. The resulting DVHs

Figure 1. Effect of the LP heuristic on the dose-volume histogram for the prostate case (solid line: initial iteration; dashed line: final iteration).
are displayed in Figure 2 for all five cases of lung cancer. DVCs 1, 3, and 5 are illustrated for all the cases. For Patient 2, the algorithm was not able to satisfy DVC3, but tried to improve tumor coverage while keeping the total lung’s DVH as close to the corresponding DVC as possible. DVC2 was obviously satisfied, since for all the cases, no volume of the PTV received a dose greater than or equal to 120% of the prescribed dose. Mean dose constraints (4 and 6) which could not be displayed on the DVH were also satisfied for all the patients (Table 3).
The outcomes of our constrained FMO model depended on the lower and upper reference boundary parameters for PTV, LT and UT, respectively. Having those parameters in the LP model is useful in controlling the optimization process, which is not possible in unconstrained optimization models. However, selecting the right parameter values can be a daunting task. Choosing boundaries that are too tight can result in an infeasible solution, so we imposed loose boundary constraints on the target, i.e., LT = 0.8 and UT = 1.2, for all cases. Further experiments were performed to show the behavior of the model. Four different settings of these boundaries were implemented for Patient 4, as shown in Figure 3. The cold spots were controlled by setting different values of LT. When we increased the lower boundary from 0.8 (Figure 3(a)) to 0.85 (Figure 3(c)), the model responded accordingly and the starting point of the target DVH curve has been shifted to ensure that no target voxels received less than 85% of the prescribed dose. Similarly, the hot spots can be controlled by UT, as seen in Figures 3(a) and (b). Figure 3(b) is the result of allowing up to a 20% overdose (UT = 1.2) to the target, while Figure 3(a) is based on a 15% overdose limit, i.e., UT = 1.15. By setting these boundaries tighter, both the
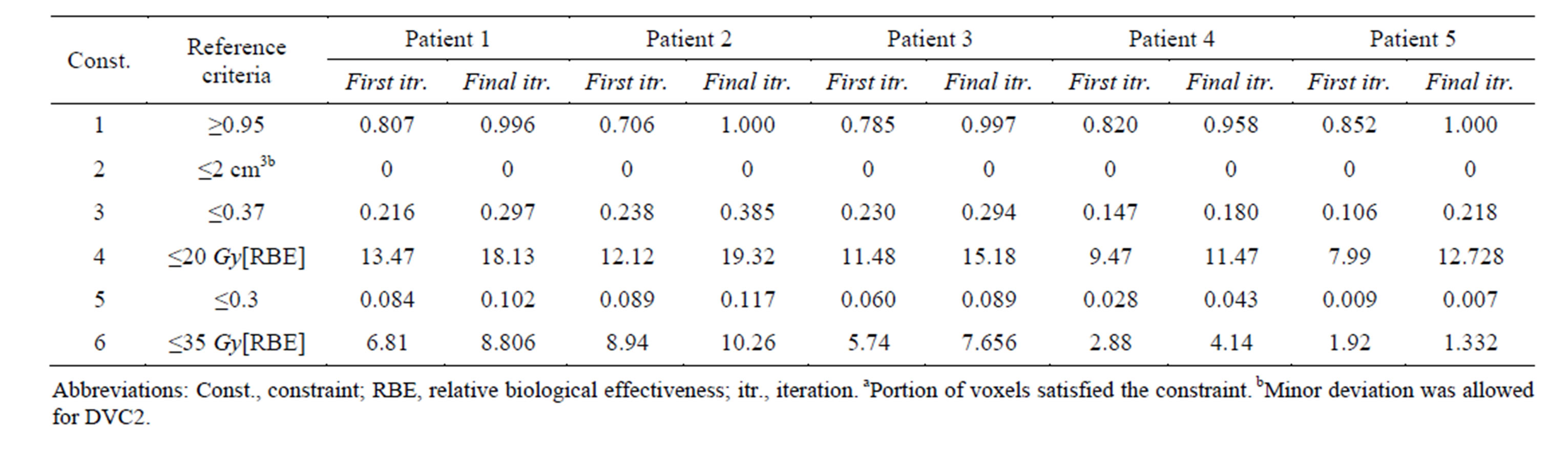
Table 3. Comparison of constraints satisfaction levelsa between the initial and final iterations of the LP heuristic in lung cancer cases.
cold spots and the hot spots were reduced accordingly. Note that such a reduction trend will continue as long as the model can find a feasible solution to meet the constraints requirements. If the model cannot find a solution to satisfy the protocol requirements, the algorithm terminates with the last solution found during the iterative process.
3.2.2. Comparison between the LP Heuristic and the NLP Model
We applied the nonlinear model solved by L-BFGS to the lung cancer cases and compared the results to those of the LP heuristic approach. Although the NLP model was able to satisfy constraints for some cases, it failed for other cases. Figure 4 compares DVHs of the LP heuristic and NLP approaches for one of these cases. All constraints except DVC1 were satisfied by the NLP approach on this case (Patient 4). Note that DVC1 corresponds to cold spots on the tumor; 91% of the tumor volume received a dose greater than or equal to 95% of the prescribed dose, which was less than the reference point on DVC1 (95%) and violated the reference criteria. When compared to the NLP FMO, the LP heuristic resulted in fewer cold spots and hot spots on the tumor. The worst cold spot on the tumor using the NLP FMO was 72% of the prescribed dose, while the worst cold spot using the LP heuristic was 80% of the prescribed dose. The worst hot spot on the tumor using the NLP FMO was more than 120% of the prescribed dose, while the worst hot spot using the LP heuristic was 112% of the prescribed dose.
3.2.3. Comparison of LP Heuristic with Eclipse 8.9
For the five cases of lung cancer, we compared the outcomes of our method to the plans from Eclipse 8.9 commercial treatment planning system (Varian Medical Systems, Palo Alto, CA, USA), which uses an NLP solver and is used at MD Anderson to treat cancer patients. Those plans are physician-approved clinical ones generated by very experienced dosimetrists, and satisfy all clinical requirements. Table 4 presents the satisfaction levels for all constraints using our heuristic algorithm and the Eclipse 8.9 system. For all patients, the LP heuristic algorithm satisfied all the constraints except DVC 3 for Patient 2. However, using the commercial treatment planning system resulted in more violations from the reference points: Constraints 2, 3, 4, and 5 for Patient 1, constraints 3 and 4 for Patient 2, and constraints 1 and 4 for Patient 3 (see Table 4). As an example, for Patient 3, 94.5% of the PTV volume received a dose greater than or equal to 95% of the prescribed dose, which was slightly below the reference point for DVC1 (95%). Also, the mean lung dose for this patient was 24.11 Gy, which violated the reference criteria corresponding to constraint 4 (≤ 20 Gy).

Figure 4. Comparison of dose-volume histograms using the LP heuristic and NLP approach for Patient 4 (solid line: NLP, dashed line: LP heuristic;blue line: target, red line: total lung, black line: heart;blue star: DVC1, red star: DVC3, black star: DVC5).
4. Discussion and Conclusions
The purpose of this study was to test an LP-based heuristic approach for FMO with DVCs using an iterative linear FMO algorithm. A major advantage of our method is that it satisfies the DVCs without increasing the complexity of the problem and while conserving its convexity. This method alleviates the tedious effort of selecting initial values of model parameters by choosing appropriate values through a simple iterative process. Starting from its initial condition, the parameter values are iteratively updated while considering trade-offs between the target coverage and the OAR sparing.
To validate the outcomes of our new algorithm, the results for cases of lung cancer were compared with those of two other approaches (NLP FMO solved by L-BFGS and Eclipse 8.9). We first illustrated the LP heuristic algorithm on a case of prostate cancer (Figure 1). Using the iterative process, the algorithm found a better solution in terms of satisfying the constraints on all OARs. We then examined the performance of all three solution methods in the five lung cancer cases. We observed the progression of the iterative LP heuristic when comparing the outcomes of the first and the last iteration (Table 3). DVCs corresponding to cold spots on the tumor were not satisfied at the initial iteration for any of the five cases. On the other hand, the satisfied portion of constraints corresponding to total lung and heart were much higher than the acceptable level (reference point). Thus, our heuristic algorithm improved the target coverage step-by-step to meet the DVC while maintaining satisfaction of the constraints for the OARs. We illustrated how to use the LP heuristic approach to control

Table 4. Comparison of constraints satisfaction levels* between LP heuristic and Eclipse 8.9.
both the hot spots and the cold spots, using four different settings of reference boundaries on the tumor (Figure 3). We showed that the LP heuristic successfully satisfied all constraints in all cases and demonstrated that properly selected tighter boundaries decreased cold spots and hot spots on the tumor as expected. These outcomes showed the advantage of using constrained linear programming optimization to control the cold and hot spots on the tumor.
We also compared the performance of the LP heuristic approach and the NLP approach in lung cancer cases and observed that the NLP failed to satisfy the DVCs in some cases (Figure 4). Note that the NLP model is an unconstrained minimization model solved using the L-BFGS method. A major drawback of this approach is that the model does not consider DVCs. Hence, there is no recourse for correcting unsatisfied constraints other than a manual trial-and-error effort to find a solution that is close to the requirements. One can try different values of initial beamlet weights and prescribed dose, or different penalty weights on the objective function, which requires a substantial amount of effort to find a clinically feasible solution. The advantage of using the LP heuristic approach is that it is not sensitive to its initial condition. It may fail to satisfy the DVCs or may result in an unacceptable plan quality at the first iteration, but through the iterative process, it will find a solution to meet the requirements.
The LP heuristic approach performed better than the Eclipse 8.9 commercial treatment planning system for the five lung cancer cases (Table 4). Unlike Eclipse 8.9, the LP heuristic approach satisfied the constraints for almost all the reference criteria for all patients. The Eclipse treatment planning system produced solutions in which eight constrains were violated in three cases.
NOTES