1. Introduction
Description logics (DLs) [2] are a family of logic-based knowledge representation formalisms with a number of computer science applications. DLs are especially wellknown to be valuable for obtaining logical foundations of web ontology languages (e.g., W3C’s ontology language OWL). Some useful DLs including a standard description logic  [3] have been studied by many researchers. Paraconsistent (or inconsistency-tolerant) description logics (PDLs) [4-13] have been studied to cope with inconsistencies which may frequently occur in an open world.
[3] have been studied by many researchers. Paraconsistent (or inconsistency-tolerant) description logics (PDLs) [4-13] have been studied to cope with inconsistencies which may frequently occur in an open world.
Some recent developments of PDLs may be briefly summarized as follows. An inconsistency-tolerant fourvalued terminological logic was originally introduced by Patel-Schneider [10], three inconsistency-tolerant constructive DLs, which are based on intuitionistic logic, were studied by Odintsov and Wansing [8,9], some paraconsistent four-valued DLs including 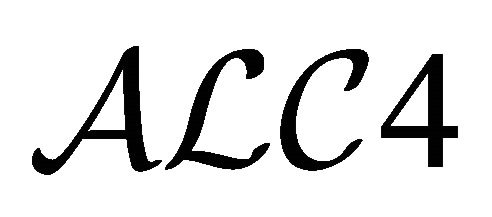 were studied by Ma et al. [4,5], some quasi-classical DLs were developed and studied by Zhang et al. [12,13], a sequent calculus for reasoning in four-valued DLs was introduced by Straccia [11], and an application of fourvalued DL to information retrieval was studied by Meghini et al. [6,7]. A PDL called
were studied by Ma et al. [4,5], some quasi-classical DLs were developed and studied by Zhang et al. [12,13], a sequent calculus for reasoning in four-valued DLs was introduced by Straccia [11], and an application of fourvalued DL to information retrieval was studied by Meghini et al. [6,7]. A PDL called 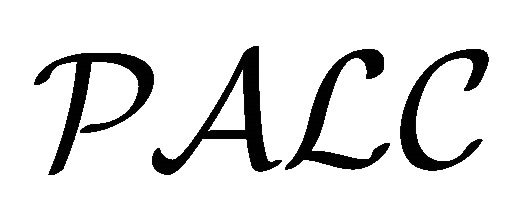 has recently been proposed by Kamide [14,15] based on the idea of Kaneiwa [16] for his multiple-interpretation DL
has recently been proposed by Kamide [14,15] based on the idea of Kaneiwa [16] for his multiple-interpretation DL .
.
The logic  [4], which is based on four-valued semantics, has a good translation into
[4], which is based on four-valued semantics, has a good translation into 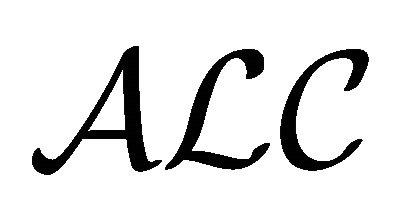 [3], and using this translation, the satisfiability problem for
[3], and using this translation, the satisfiability problem for 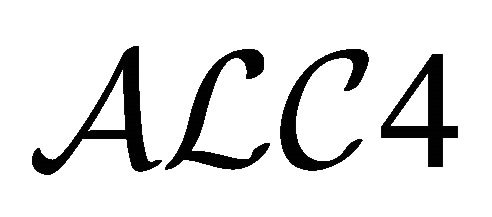 is shown to be decidable. But,
is shown to be decidable. But,  and its variations have no classical negation (or complement). As mentioned in [17], classical and paraconsistent negations are known to be both useful for some knowledgebased systems. The quasi-classical DLs in [12,13], which are based on quasi-classical semantics, have the classical negation. But, translations of the quasi-classical DLs into the corresponding standard DLs were not proposed.
and its variations have no classical negation (or complement). As mentioned in [17], classical and paraconsistent negations are known to be both useful for some knowledgebased systems. The quasi-classical DLs in [12,13], which are based on quasi-classical semantics, have the classical negation. But, translations of the quasi-classical DLs into the corresponding standard DLs were not proposed. 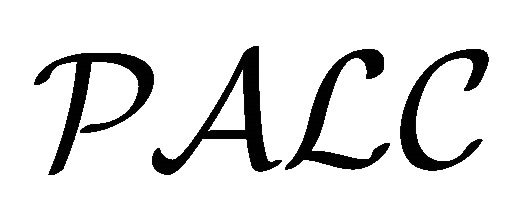 [14], which is based on dual-interpretation semantics, has both the merits of
[14], which is based on dual-interpretation semantics, has both the merits of 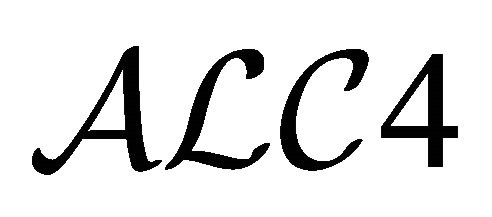 and the quasiclassical DLs, i.e., it has the translation and the classical negation. The semantics of
and the quasiclassical DLs, i.e., it has the translation and the classical negation. The semantics of  is taken over from the dual-consequence Kripke-style semantics for Nelson’s paraconsistent four-valued logic N4 with strong negation [18,19]. The constructive PDLs in [8] are based on single-interpretation semantics, which can be seen as a DL-version of the single-consequence Kripke-style semantics for N4 [20].
is taken over from the dual-consequence Kripke-style semantics for Nelson’s paraconsistent four-valued logic N4 with strong negation [18,19]. The constructive PDLs in [8] are based on single-interpretation semantics, which can be seen as a DL-version of the single-consequence Kripke-style semantics for N4 [20].
The following natural question arises: What is the relationship among the single-interpretation semantics of the constructive PDLs, the dual-interpretation semantics of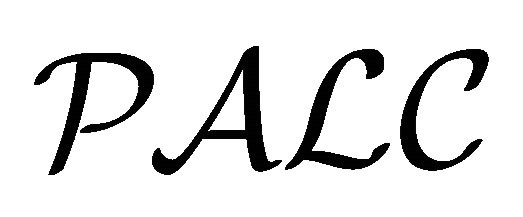 , the four-valued semantics of
, the four-valued semantics of , and the quasi-classical semantics of the quasi-classical DLs? This paper gives an answer to this question: These paraconsistent semantics are essentially the same semantics in the sense that some fragments of these PDLs are logically equivalent. More precisely, we show the following. A new PDL, called
, and the quasi-classical semantics of the quasi-classical DLs? This paper gives an answer to this question: These paraconsistent semantics are essentially the same semantics in the sense that some fragments of these PDLs are logically equivalent. More precisely, we show the following. A new PDL, called , is introduced based on a generalized quasi-classical semantics. It can be seen that the quasi-classical semantics and the fourvalued semantics are special cases of the
, is introduced based on a generalized quasi-classical semantics. It can be seen that the quasi-classical semantics and the fourvalued semantics are special cases of the  semantics. An equivalence between
semantics. An equivalence between  and (a slightly modified version of)
and (a slightly modified version of)  is proved. A new PDL, called
is proved. A new PDL, called , is introduced based on a modified single-interpretation semantics. An equivalence between
, is introduced based on a modified single-interpretation semantics. An equivalence between  and (a slightly modified version of)
and (a slightly modified version of)  is proved. These results mean that the existing applications and theoretical results (e.g., decidability, complexity, embeddability and completeness) can be shared in these paraconsistent semantics.
is proved. These results mean that the existing applications and theoretical results (e.g., decidability, complexity, embeddability and completeness) can be shared in these paraconsistent semantics.
It is remarked that this paper does not give a “comprehensive” comparison, since the existing paraconsistent semantics have some different constructors (or logical connectives), i.e., it is difficult to compare the whole parts of these existing semantics. But, this paper gives an “essential” comparison with respect to the common part with the constructors  (paraconsistent negation),
(paraconsistent negation),  (intersection),
(intersection),  (union),
(union),  (universal concept quantification) and
(universal concept quantification) and  (existential concept quantification). To obtain such a comparison with some exact proofs, we need some small modifications of the existing paraconsistent semantics. Since all the logics discussed in this paper are defined as semantics, we will occasionally identify the semantics with the logic determined by it.
(existential concept quantification). To obtain such a comparison with some exact proofs, we need some small modifications of the existing paraconsistent semantics. Since all the logics discussed in this paper are defined as semantics, we will occasionally identify the semantics with the logic determined by it.
The contents of this paper are then summarized as follows.
In Section 2, the essential parts of the existing paraconsistent semantics (i.e., 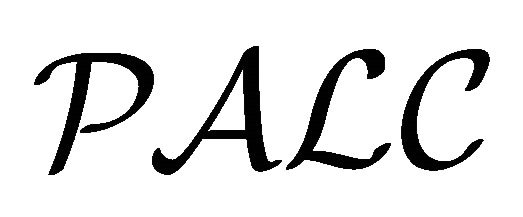 -semantics, four-valued semantics, quasi-classical semantics and single interpretation semantics) are addressed.
-semantics, four-valued semantics, quasi-classical semantics and single interpretation semantics) are addressed.
In Section 3, two new semantics (i.e., the  - semantics and the
- semantics and the  -semantics) are introduced, and the equivalence among the
-semantics) are introduced, and the equivalence among the  -semantics, the
-semantics, the  -semantics and the
-semantics and the 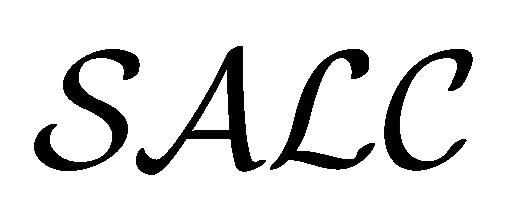 -semantics is proved. It is observed that the essential parts of the four-valued semantics and the quasi-classical semantics are special cases of the
-semantics is proved. It is observed that the essential parts of the four-valued semantics and the quasi-classical semantics are special cases of the  -semantics. It is also observed that the
-semantics. It is also observed that the 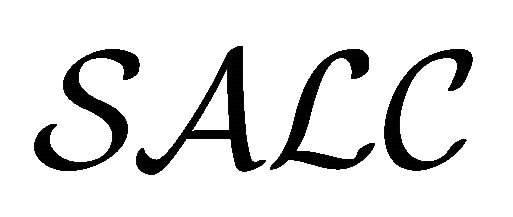 -semantics is regarded as a classical version of the
-semantics is regarded as a classical version of the  -semantics (single-interpretation semantics) for a constructive description logic introduced by Odintsov and Wansing.
-semantics (single-interpretation semantics) for a constructive description logic introduced by Odintsov and Wansing.
In Section 4, some remarks on constructive PDLs and temporal DLs.
In Section 5, this paper is concluded.
2. Existing Paraconsistent Semantics
2.1. 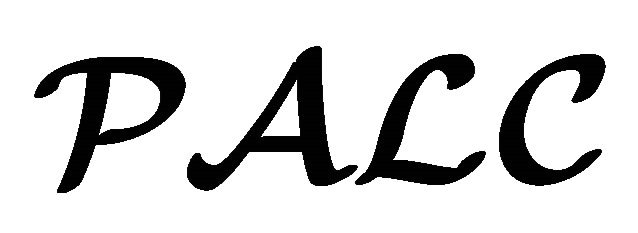 Semantics
Semantics
In the following, we present the logic 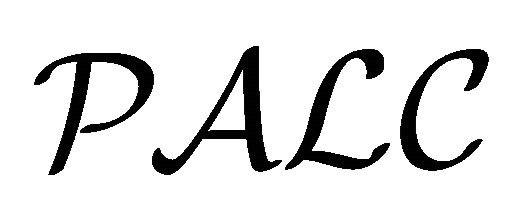 [14], which has dual-interpretation semantics. The
[14], which has dual-interpretation semantics. The  - concepts are constructed from atomic concepts, roles, ~ (paraconsistent negation),
- concepts are constructed from atomic concepts, roles, ~ (paraconsistent negation),  (classical negation or complement),
(classical negation or complement),  (intersection),
(intersection),  (union),
(union), 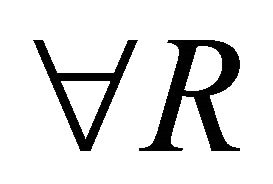 (universal concept quantification) and
(universal concept quantification) and  (existential concept quantification). We use the letters
(existential concept quantification). We use the letters  and
and 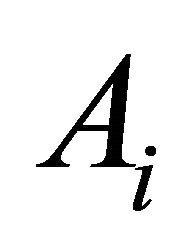 for atomic concepts, the letter
for atomic concepts, the letter 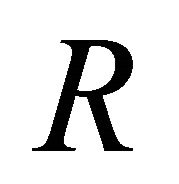 for roles, and the letters
for roles, and the letters  and
and  for concepts.
for concepts.
Definition 2.1 Concepts  are defined by the following grammar:
are defined by the following grammar:

Definition 2.2 A paraconsistent interpretation  is a structure
is a structure  where 1)
where 1)  is a non-empty set2)
is a non-empty set2)  is an interpretation function which assigns to every atomic concept
is an interpretation function which assigns to every atomic concept  a set
a set  and to every role
and to every role  a binary relation
a binary relation 3)
3) 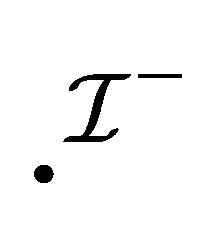 is an interpretation function which assigns to every atomic concept
is an interpretation function which assigns to every atomic concept  a set
a set 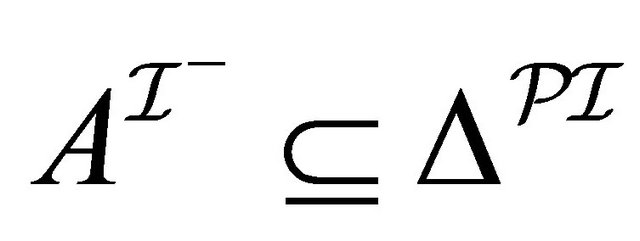 and to every role
and to every role  a binary relation
a binary relation 4) for any role
4) for any role ,
, .
.
The interpretation functions are extended to concepts by the following inductive definitions:
 , (1)
, (1)
 , (2)
, (2)
 , (3)
, (3)
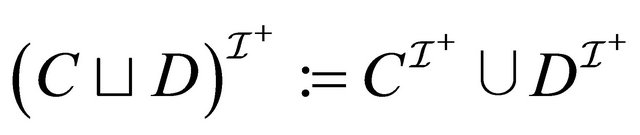 , (4)
, (4)
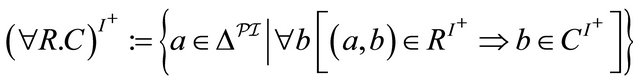 , (5)
, (5)
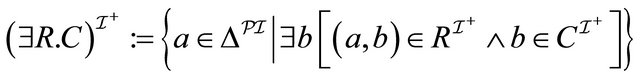 , (6)
, (6)
 , (7)
, (7)
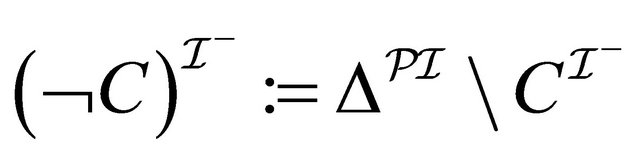 , (8)
, (8)
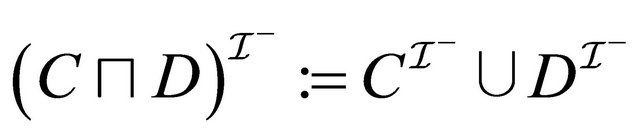 , (9)
, (9)
 , (10)
, (10)
 , (11)
, (11)
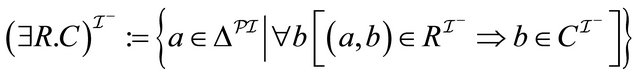 .(12)
.(12)
An expression 
 is defined as
is defined as . A paraconsistent interpretation
. A paraconsistent interpretation  is a model of a concept
is a model of a concept  (denoted as
(denoted as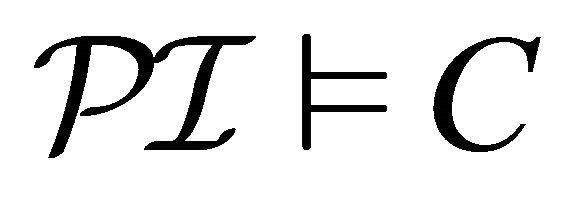 ) if
) if 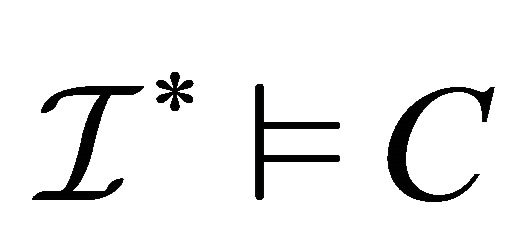
 . A concept
. A concept  is said to be satisfiable in
is said to be satisfiable in  if there exists a paraconsistent interpretation
if there exists a paraconsistent interpretation  such that
such that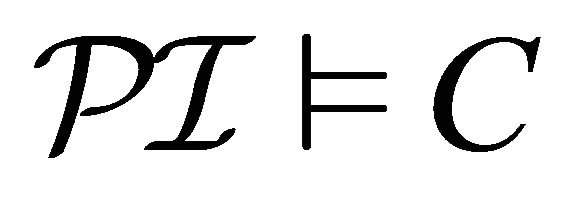 .
.
The interpretation functions 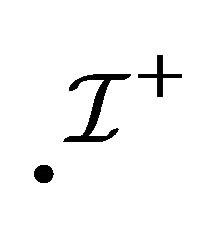 and
and 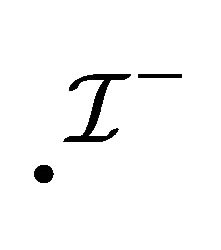 are intended to represent “verification” (or “support of truth”) and “falsification” (or “support of falsity”), respectively. It is noted that
are intended to represent “verification” (or “support of truth”) and “falsification” (or “support of falsity”), respectively. It is noted that  includes
includes  [3] as a subsystem since
[3] as a subsystem since  in
in  includes
includes  in
in .
.
Intuitively speaking,  is constructed based on the following additional axiom schemes for
is constructed based on the following additional axiom schemes for :
:
 , (1)
, (1)
 , (2)
, (2)
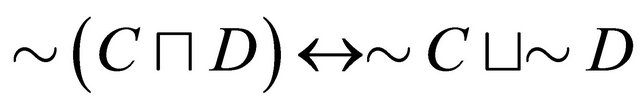 , (3)
, (3)
 , (4)
, (4)
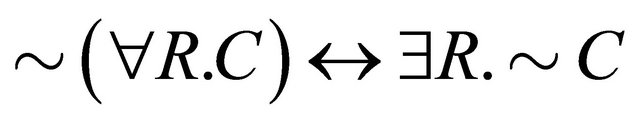 , (5)
, (5)
 . (6)
. (6)
It is noted that the interpretations for ~ and  in
in  correspond to the axiom scheme
correspond to the axiom scheme , which means that ~ and
, which means that ~ and  are self duals with respect to
are self duals with respect to  and ~, respectively. We now give an intuitive example for this axiom. Let
and ~, respectively. We now give an intuitive example for this axiom. Let  stand for the claim that
stand for the claim that  is poor, and let
is poor, and let 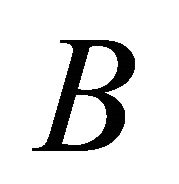 stand for the claim that
stand for the claim that  is rich. Intuitively,
is rich. Intuitively,  is verified (falsified) iff
is verified (falsified) iff 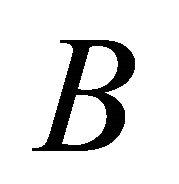 is falsified (verified, respectively). Suppose now that
is falsified (verified, respectively). Suppose now that 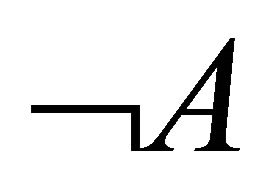 is indeed falsified. This should mean that it is verified that
is indeed falsified. This should mean that it is verified that  is poor or neither poor or rich. But this is the case iff
is poor or neither poor or rich. But this is the case iff 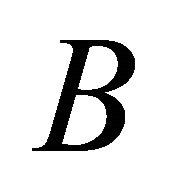 is not verified, which means that
is not verified, which means that  is not falsified.
is not falsified.
For each concept , we can take one of the following cases:
, we can take one of the following cases:
1)  is verified, i.e.,
is verified, i.e., 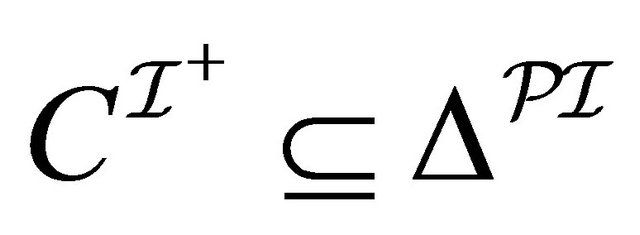 2)
2)  is falsified, i.e.,
is falsified, i.e.,  3)
3)  is both verified and falsified4)
is both verified and falsified4)  is neither verified nor falsified.
is neither verified nor falsified.
Thus,  may be regarded as a four-valued logic.
may be regarded as a four-valued logic.
In general, a semantic consequence relation ‘is called paraconsistent with respect to a negation connective: if there are formulas  and
and 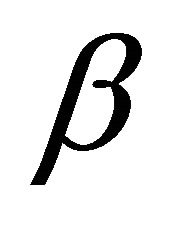 such that
such that  does not hold. In the case of
does not hold. In the case of , assume a paraconsistent interpretation
, assume a paraconsistent interpretation 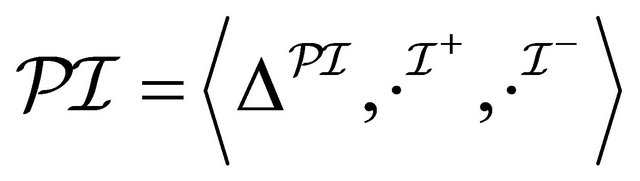 such that
such that ,
, 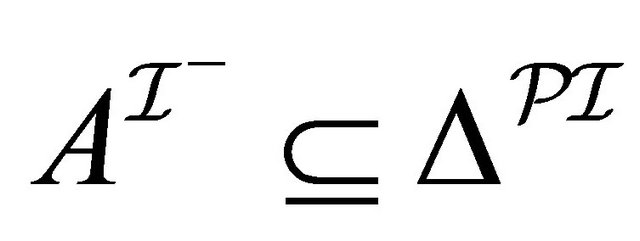 and not-
and not-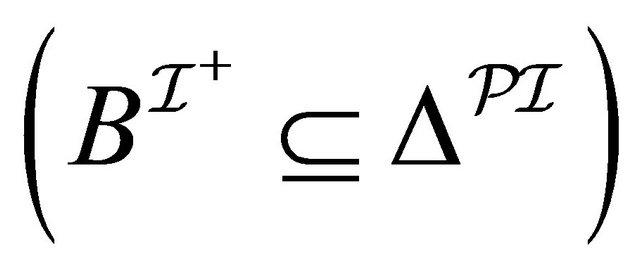 for a pair of distince atomic concepts
for a pair of distince atomic concepts  and
and . Then,
. Then,  does not hold, and hence
does not hold, and hence 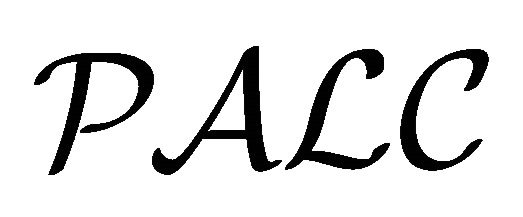 is paraconsistent with respect to:. It is remarked that
is paraconsistent with respect to:. It is remarked that  is not paraconsistent with respect to
is not paraconsistent with respect to .
.
Next, we explain about some differences and similarities between 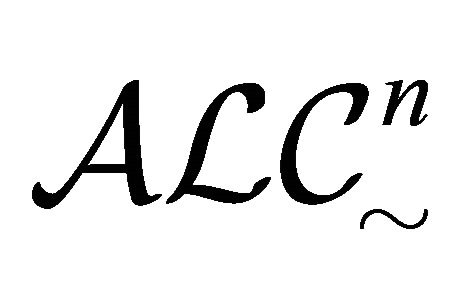 [16] and
[16] and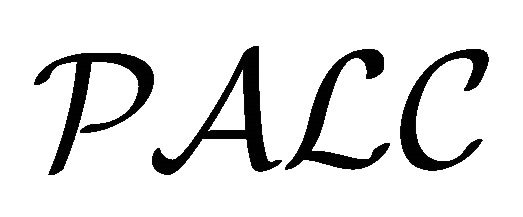 . In
. In
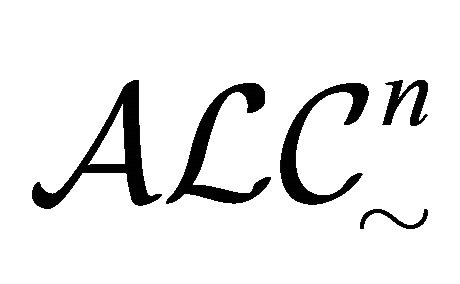 , the set
, the set 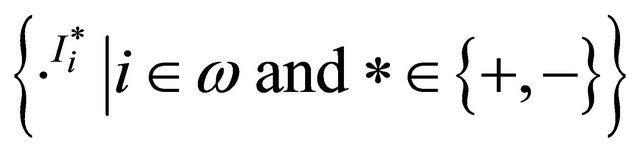 of multiple interpretation functions were used. These interpretation functions include the following characteristic conditions for negations:
of multiple interpretation functions were used. These interpretation functions include the following characteristic conditions for negations:
1) for any atomic concept ,
, 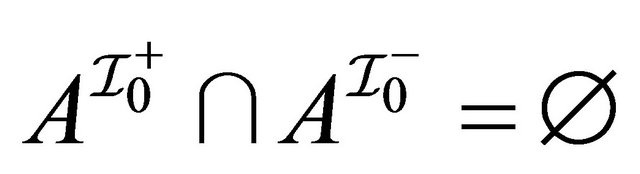 2) for any atomic concept
2) for any atomic concept ,
, 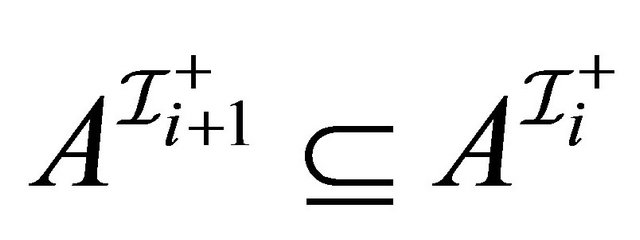 3) for any atomic concept
3) for any atomic concept ,
, 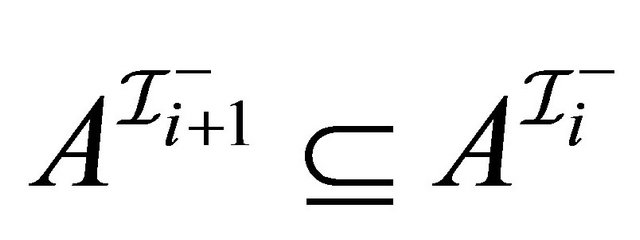 4)
4)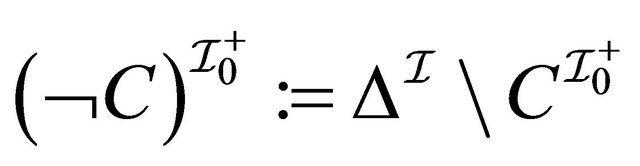 5)
5) 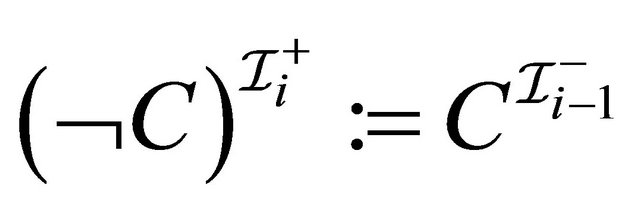 with
with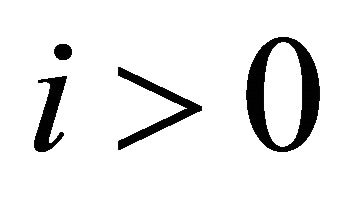 6)
6)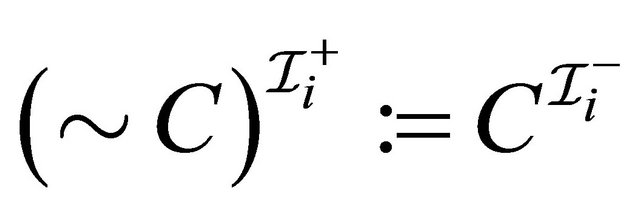 7)
7) 8)
8)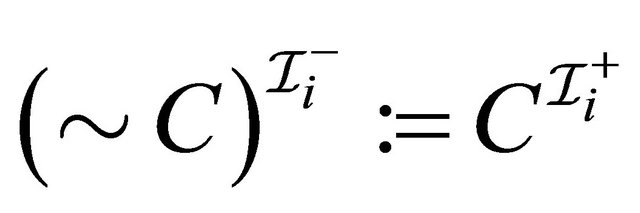 .
.
It is remarked that the condition 1 above means that  is not paraconsistent with respect to
is not paraconsistent with respect to . The subsystem (or special case)
. The subsystem (or special case) 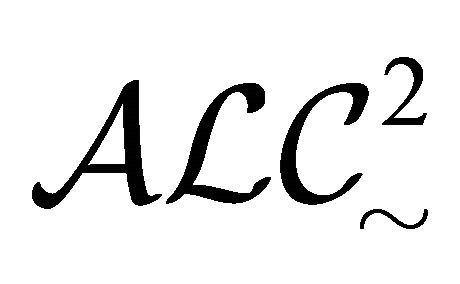 (of
(of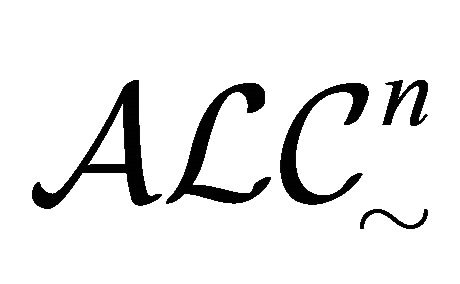 ), which adopts two interpretation functions
), which adopts two interpretation functions  and
and , is similar to
, is similar to . The conditions for the constructors
. The conditions for the constructors  and
and  of
of  are almost the same as those of
are almost the same as those of . The main differences are presented as follows:
. The main differences are presented as follows:
1) 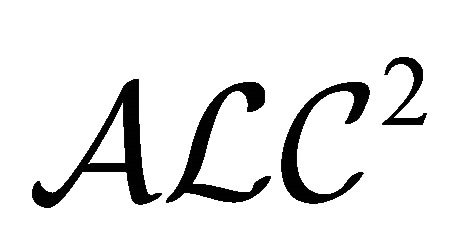 has the “non-paraconsistent” condition: for any atomic concept
has the “non-paraconsistent” condition: for any atomic concept ,
,
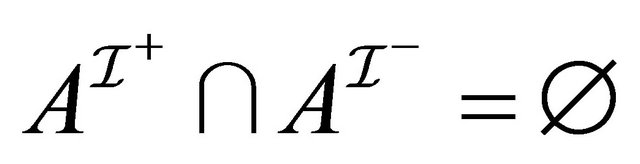 but
but  has no this condition2)
has no this condition2)  adopts the condition:
adopts the condition:
 but
but  has no this condition and adopts the condition:
has no this condition and adopts the condition:
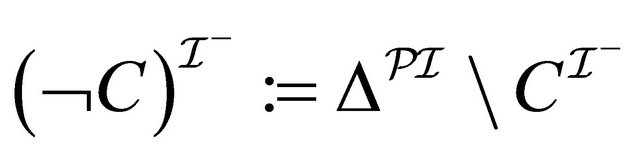
instead of it.
2.2. Four-Valued Semantics and Quasi-Classical Semantics
Some four-valued semantics in [4] were based on ,
,  , DL-Lite, etc., and the quasi-classical semantics in [13] was based on
, DL-Lite, etc., and the quasi-classical semantics in [13] was based on . The four-valued semantics in [4] has no classical negation, but has some new inclusion constructors such as strong inclusion. In addition, the quasi-classical semantics in [13] has two kinds of definitions called QC weak semantics and QC strong semantics. The following explanation is based on
. The four-valued semantics in [4] has no classical negation, but has some new inclusion constructors such as strong inclusion. In addition, the quasi-classical semantics in [13] has two kinds of definitions called QC weak semantics and QC strong semantics. The following explanation is based on  and QC weak semantics. We use the common language based on
and QC weak semantics. We use the common language based on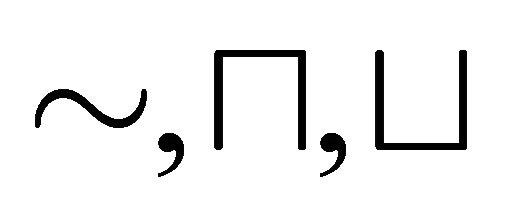 ,
, 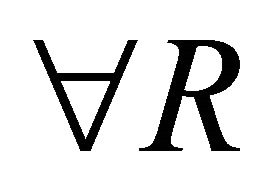 ,
,  and/or
and/or .
.
We cannot compare the existing paraconsistent semantics (i.e., the four-valued semantics, the quasi-classical semantics, the single-interpretation semantics and the dual-interpretation semantics) themselves since the underlying DLs are different. Moreover, the motivations of introducing the existing semantics are completely different. For example, in the quasi-classical semantics, the main motivation is to satisfy three important inference rules: modus ponens, modus tollens and disjunctive syllogism. These inference rules are strongly dependent on a specific inclusion constructor 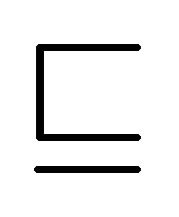 and a specific QC entailment
and a specific QC entailment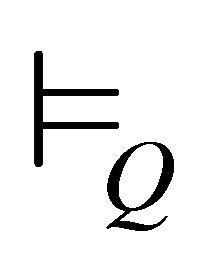 . Thus, our comparison without
. Thus, our comparison without  is regarded as not so comprehensive or essential in the sense of the original motivation of the quasi-classical semantics.
is regarded as not so comprehensive or essential in the sense of the original motivation of the quasi-classical semantics.
The following definition is a slight modification of the definition of  [4].
[4].
Definition 2.3 (Four-valued semantics) A fourvalued interpretation 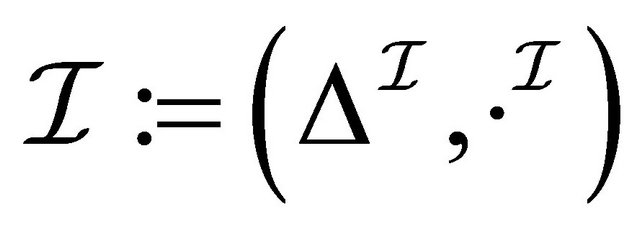 is defined using a pair
is defined using a pair 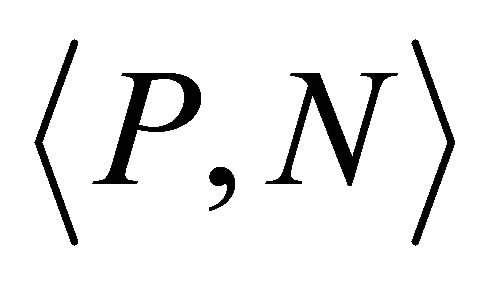 of subsets of
of subsets of  and the projection functions
and the projection functions 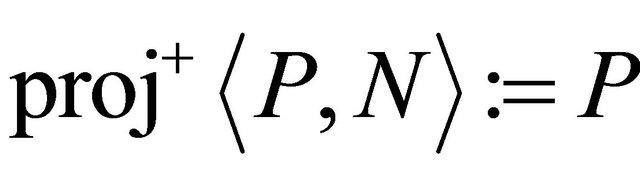 and
and . The interpretations are then defined as follows:1
. The interpretations are then defined as follows:1
1) a role 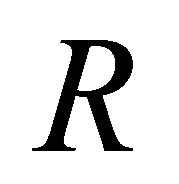 is assigned to a relation
is assigned to a relation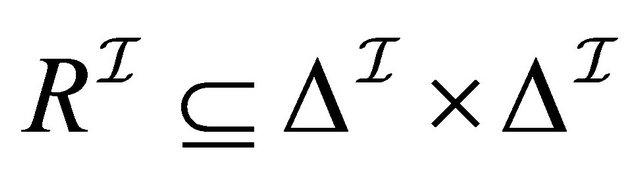 2) for an atomic concept
2) for an atomic concept ,
, 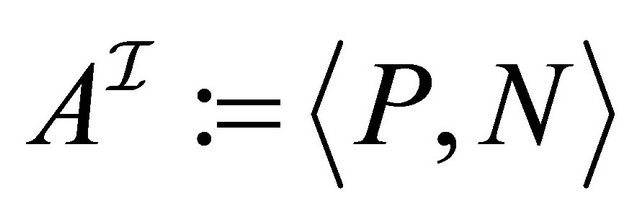 where
where 3)
3)  if
if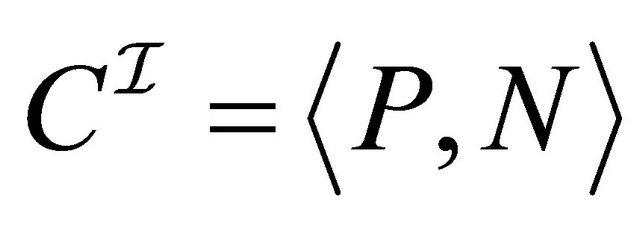 4)
4)  if
if  for
for 5)
5) 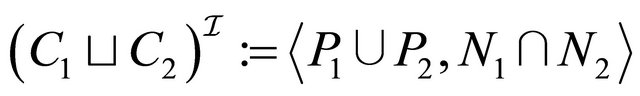 if
if 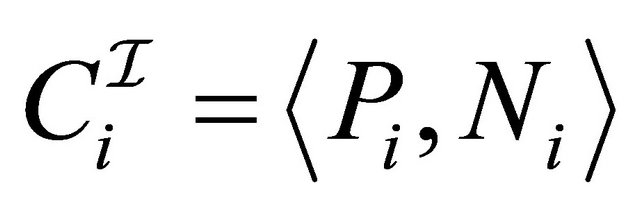 for
for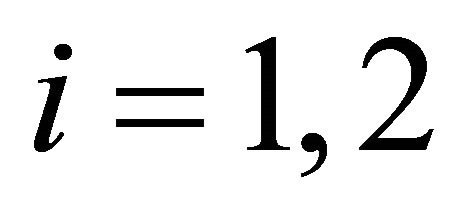 6)
6) 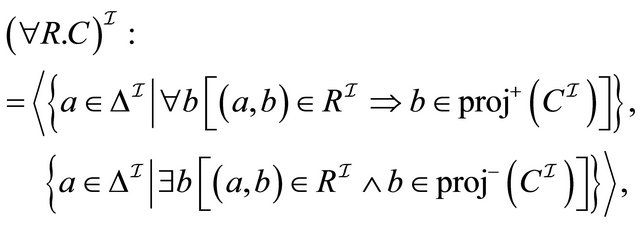
7) 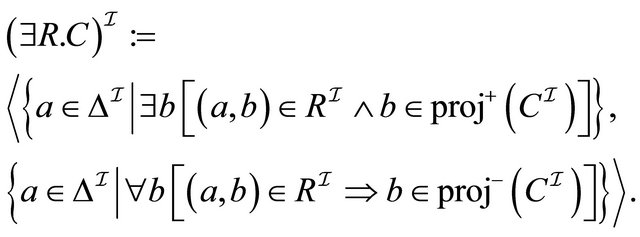
In the four-valued semantics for  [4], different kinds of implications were introduced:
[4], different kinds of implications were introduced:
1) 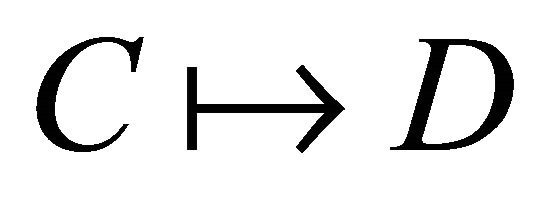 (material inclusion)
(material inclusion)
2) 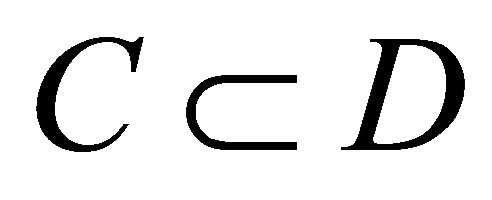 (internal inclusion)
(internal inclusion)
3)  (strong inclusion).
(strong inclusion).
The interpretations of ,
, 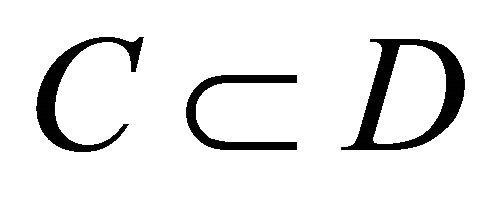 and
and  are respectively presented as follows:
are respectively presented as follows:
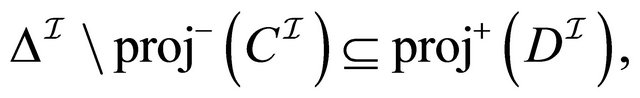 (1)
(1)
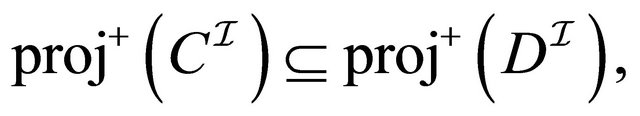 (2)
(2)
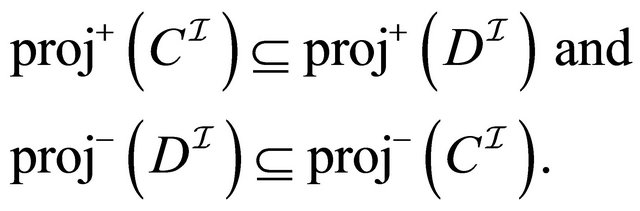 (3)
(3)
These implications provide flexible way to model inconsistent ontologies.
The extension of four-valued semantics to the expressive description logic , and the extensions of four-valued semantics to some tractable description logics
, and the extensions of four-valued semantics to some tractable description logics , Horn-DLs and DL-Lite family were studied in [5].
, Horn-DLs and DL-Lite family were studied in [5].
Next, we discuss about quasi-classical description logic. The following definition is a slight modification of the definition of quasi-classical description logics [12, 13].
Definition 2.4 (Quasi-classical semantics) A quasiclassical weak interpretation 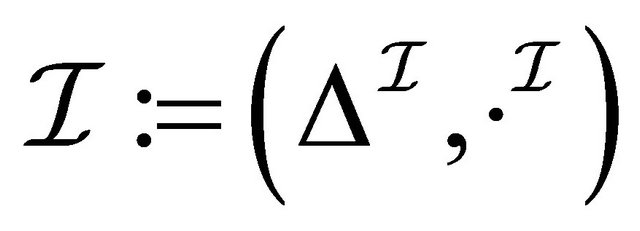 is defined using a pair
is defined using a pair  of subsets of
of subsets of 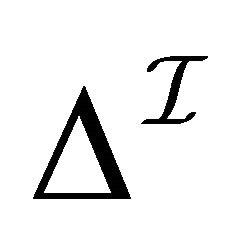 without using projection functions. The interpretations are then defined as follows:2
without using projection functions. The interpretations are then defined as follows:2
1) a role  is assigned to a pair
is assigned to a pair 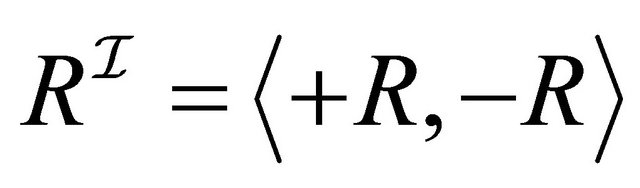 of binary relations
of binary relations 2) for an atomic concept
2) for an atomic concept ,
,  where
where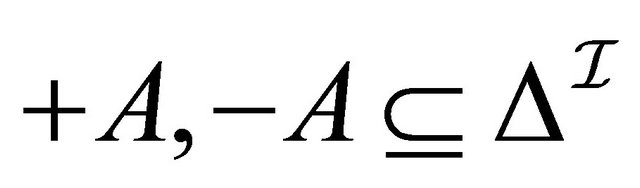 3)
3) 4)
4)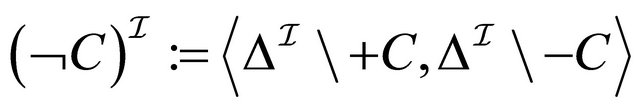 5)
5)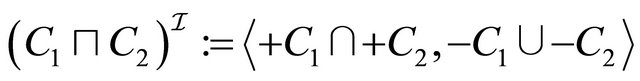 6)
6)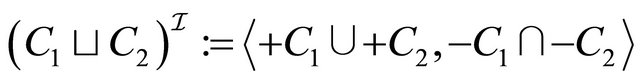 7)
7) 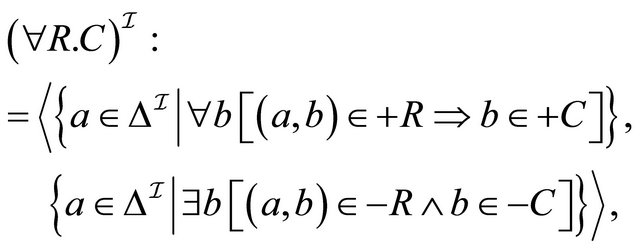
8) 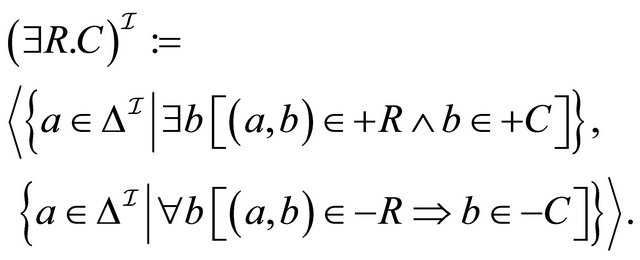
The quasi-classical semantics for QC  [12] were extended to that of QC
[12] were extended to that of QC  [13] to handle inconsistent ontologies. It composes two kinds of semantics, i.e., QC weak semantics
[13] to handle inconsistent ontologies. It composes two kinds of semantics, i.e., QC weak semantics  and QC strong semantics
and QC strong semantics . QC weak semantics inherits the characteristics of four-valued semantics, and QC strong semantics redefines the interpretation for disjunction and conjunction of concepts to make the three important inference rules (i.e., modus ponens, modus tollens and disjunctive syllogism) hold.
. QC weak semantics inherits the characteristics of four-valued semantics, and QC strong semantics redefines the interpretation for disjunction and conjunction of concepts to make the three important inference rules (i.e., modus ponens, modus tollens and disjunctive syllogism) hold.
Let  be a QC entailment and
be a QC entailment and  be a paraconsistent negation connective, which is represented as ~ in the above definition. Then, the following hold:
be a paraconsistent negation connective, which is represented as ~ in the above definition. Then, the following hold:
1)  (modus ponense)
(modus ponense)
2)  (modus tollens)
(modus tollens)
3) 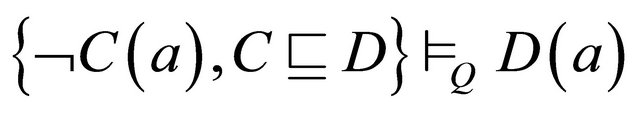 (disjunctive syllogism).
(disjunctive syllogism).
Two basic query entailment problems (i.e., instance checking and subsumption checking) were also defined and discussed in [13]. It was also shown that the two basic inference problems can be reduced into the  consistency problem.
consistency problem.
Finally in this subsection, it is remarked that the pairing functions used in the four-valued and quasiclassical semantics have been used in some algebraic semantics for Nelson’s logics (see e.g., [21] and the references therein). On the other hand, the semantics of  is defined using two interpretation functions
is defined using two interpretation functions  and
and  instead of the pairing functions. These interpretation functions have been used in some Kripketype semantics for Nelson’s logics (see e.g., [22] and the references therein). It will be shown in the next section that the “horizontal” semantics using paring functions and the “vertical” semantics using two kinds of interpretation functions have thus essentially the same meaning.
instead of the pairing functions. These interpretation functions have been used in some Kripketype semantics for Nelson’s logics (see e.g., [22] and the references therein). It will be shown in the next section that the “horizontal” semantics using paring functions and the “vertical” semantics using two kinds of interpretation functions have thus essentially the same meaning.
2.3. Single-Interpretation Semantics
Three constructive PDLs, which have single-interpretation semantics, were introduced and studied by Odintsov and Wansing [8]:
1) : Constructive version of
: Constructive version of . It is obtained via a translation into first-order classical logic. A tableau algorithm for
. It is obtained via a translation into first-order classical logic. A tableau algorithm for  was presented in [9].
was presented in [9].
2) : It is obtained via a translation into the quantified N4. The role restrictions
: It is obtained via a translation into the quantified N4. The role restrictions  and
and 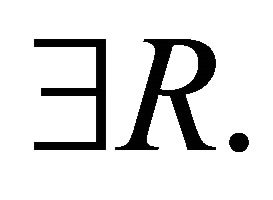 are not dual.
are not dual.
3) : It is obtained via an alternative translation into the quantified N4. The role restrictions
: It is obtained via an alternative translation into the quantified N4. The role restrictions  and
and  are dual. The decidability of
are dual. The decidability of  was obtained in [8] from a translation into Fischer Servi’s intuitionistic modal logic.
was obtained in [8] from a translation into Fischer Servi’s intuitionistic modal logic.
We now give an overview of  as follows.
as follows.  has no classical negation connective
has no classical negation connective , but has a paraconsistent negation connective
, but has a paraconsistent negation connective . Also it has no classical implication (or classical inclusion), but has a constructive implication (or constructive inclusion)
. Also it has no classical implication (or classical inclusion), but has a constructive implication (or constructive inclusion) .
.
 uses interpretations
uses interpretations 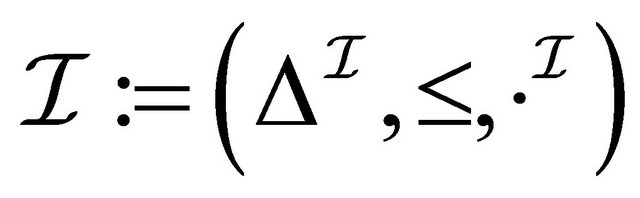 where 1)
where 1) 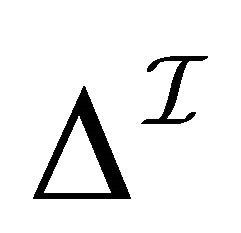 is a non-empty set2)
is a non-empty set2)  is a reflexive and transitive relation of informational accessibility3)
is a reflexive and transitive relation of informational accessibility3) 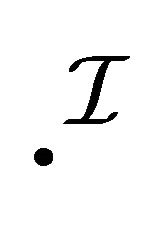 is an interpretation function with some conditions, e.g.a) it maps every atomic concept
is an interpretation function with some conditions, e.g.a) it maps every atomic concept  to a subset of
to a subset of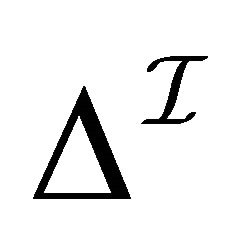 b) it maps every negated atomic concept
b) it maps every negated atomic concept 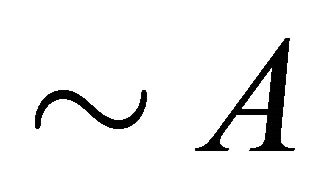 to a subset of
to a subset of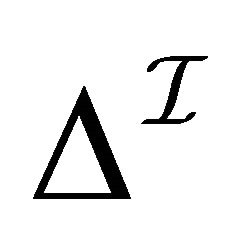 .
.
The interpretation function has the following conditions:
1) for an atomic concept ,
,  2) for an atomic concept
2) for an atomic concept ,
,  3)
3) 4)
4) 5)
5)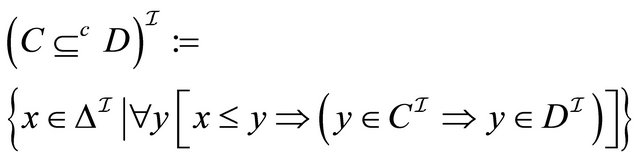 6)
6)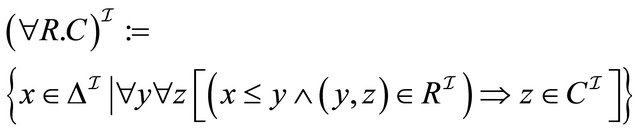 7)
7) 8)
8) 9)
9) 10)
10) 11)
11) 12)
12)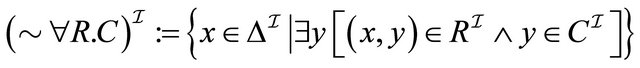 13)
13)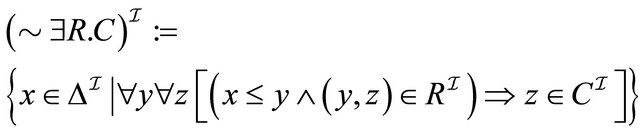 .
.
It is remarked that the order relation  needs some more conditions. For the details, see [8,9].
needs some more conditions. For the details, see [8,9].
3. New Paraconsistent Semantics
3.1.  Semantics
Semantics
Similar notions and terminologies for  are also used for the new logic
are also used for the new logic . The
. The  -concepts are the same as the
-concepts are the same as the  -concepts. The
-concepts. The  semantics is defined as a generalization and modification of the quasi-classical weak semantics defined in Definition 2.4. Thus, we use the term “quasi-classical” in the following definition.
semantics is defined as a generalization and modification of the quasi-classical weak semantics defined in Definition 2.4. Thus, we use the term “quasi-classical” in the following definition.
Definition 3.1 A quasi-classical interpretation 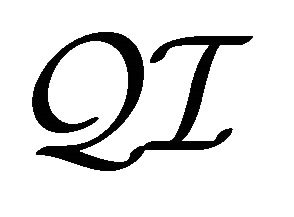 is a structure
is a structure  where 1)
where 1) 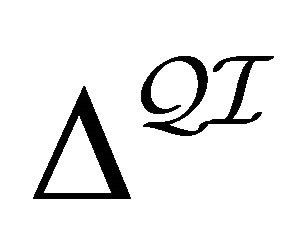 is a non-empty set2)
is a non-empty set2) 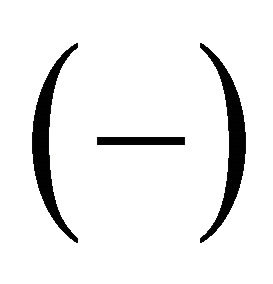
 is a positive (negative, resp.) polarity function which assigns to every atomic concept
is a positive (negative, resp.) polarity function which assigns to every atomic concept  a set
a set
 (
(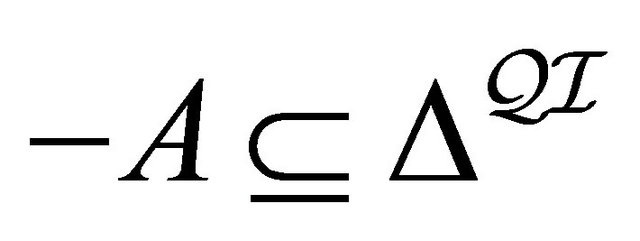 , resp.)3)
, resp.)3) 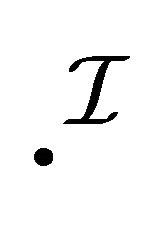 is an interpretation function which assigns to every atomic concept
is an interpretation function which assigns to every atomic concept  a pair
a pair  of sets
of sets 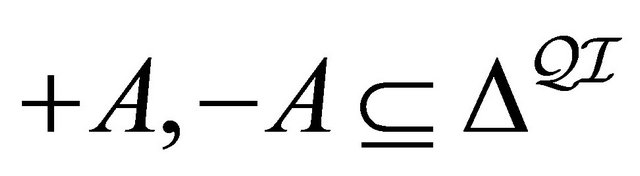 and to every role
and to every role 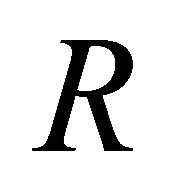 a pair
a pair 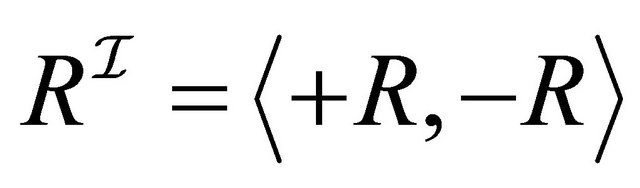 of binary relations
of binary relations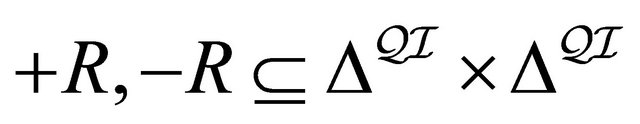 4) for any role
4) for any role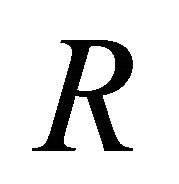 ,
,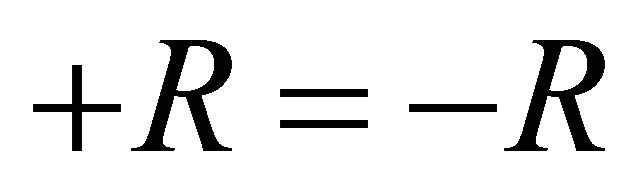 .
.
The polarity functions are extended to concepts by the following inductive definitions:
 , (1)
, (1)
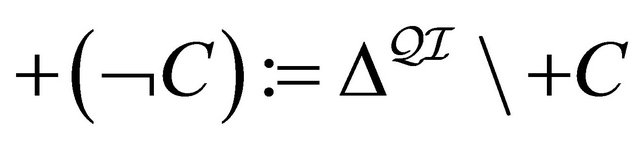 , (2)
, (2)
 , (3)
, (3)
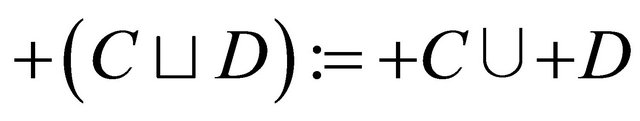 , (4)
, (4)
 , (5)
, (5)
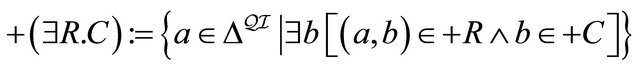 , (6)
, (6)
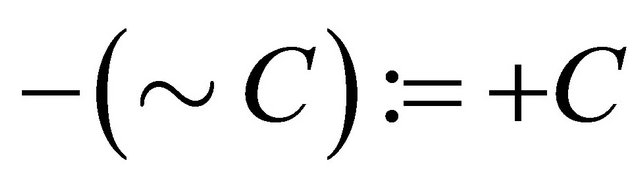 , (7)
, (7)
 , (8)
, (8)
 , (9)
, (9)
 , (10)
, (10)
 , (11)
, (11)
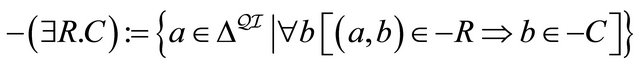 . (12)
. (12)
The interpretation function is extended to concepts by:
 .
.
An expression 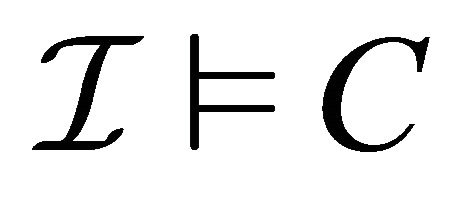 is defined as
is defined as  and
and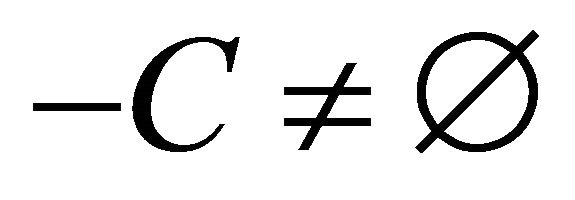 . A quasi-classical interpretation
. A quasi-classical interpretation
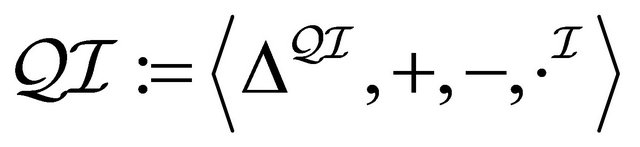 is a model of a concept
is a model of a concept 
(denoted as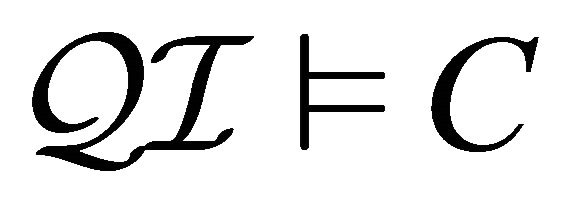 ) if
) if . A concept
. A concept  is said to be satisfiable in
is said to be satisfiable in  if there exists a quasiclassical interpretation
if there exists a quasiclassical interpretation 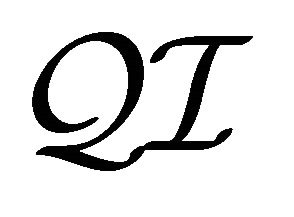 such that
such that .
.
We have the following propositions, which mean that Definition 3.1 is essentially the same definitions as those of the original quasi-classical [12,13] and four-valued [4,5] semantics. See Definitions 2.4 and 2.3.
Proposition 3.2 Let  be an interpretation function on a quasi-classical interpretation
be an interpretation function on a quasi-classical interpretation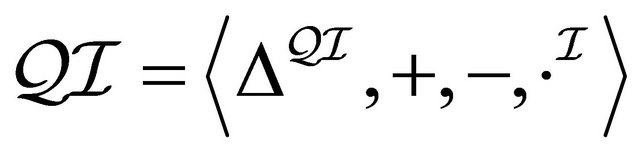 . Then, the following conditions hold:
. Then, the following conditions hold:
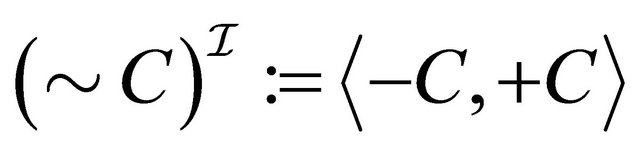 , (1)
, (1)
 , (2)
, (2)
 , (3)
, (3)
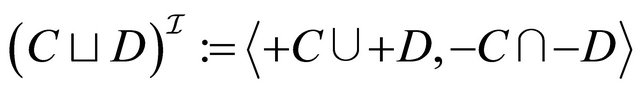 , (4)
, (4)
 (5)
(5)
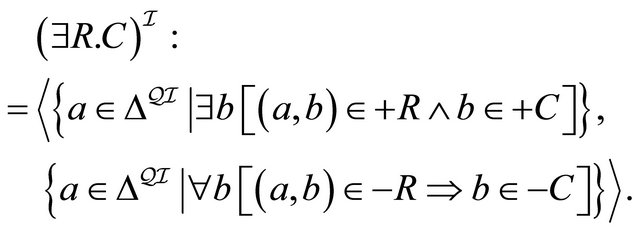 (6)
(6)
Proposition 3.3 Let 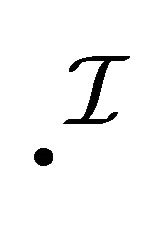 be an interpretation function on a quasi-classical interpretation
be an interpretation function on a quasi-classical interpretation . Let
. Let  and
and  be now represented by P and N, respectively. Also,
be now represented by P and N, respectively. Also, 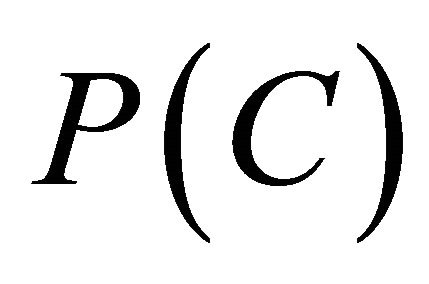 and
and  for a concept
for a concept  be represented by
be represented by  and
and , respectively. Define
, respectively. Define  and
and 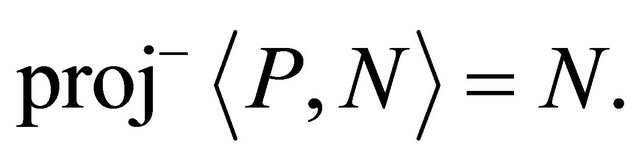 Then, the following conditions hold:
Then, the following conditions hold:
 , (1)
, (1)
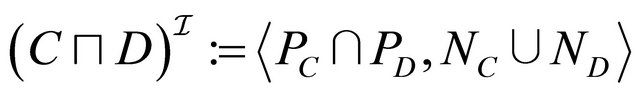 , (2)
, (2)
 , (3)
, (3)
 (4)
(4)
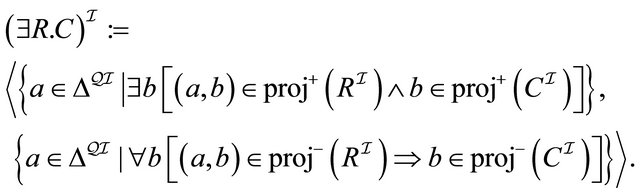 (5)
(5)
Next, we show the equivalence between  and
and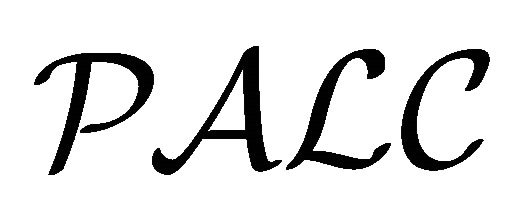 .
.
Theorem 3.4 (Equivalence between 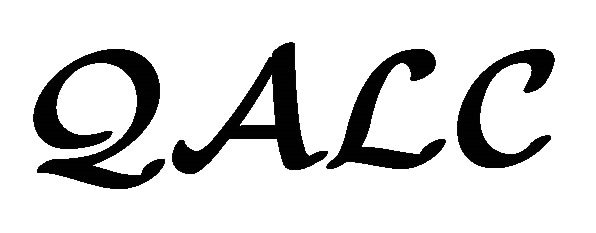 and
and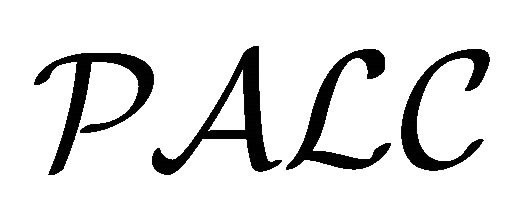 ) For any concept
) For any concept ,
,  is satisfiable in
is satisfiable in 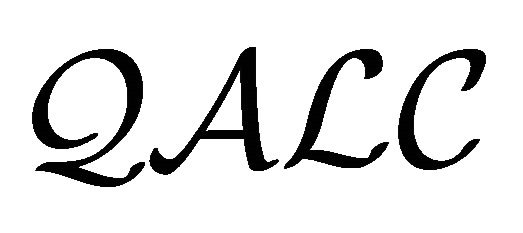 iff
iff  is satisfiable in
is satisfiable in .
.
Proof.
 : Suppose that
: Suppose that 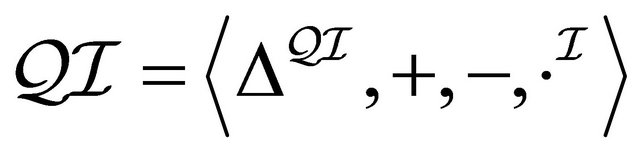 is a quasi-classical interpretation. Then, it is sufficient to construct a paraconsistent interpretation
is a quasi-classical interpretation. Then, it is sufficient to construct a paraconsistent interpretation
 such that, for any concept
such that, for any concept ,
,
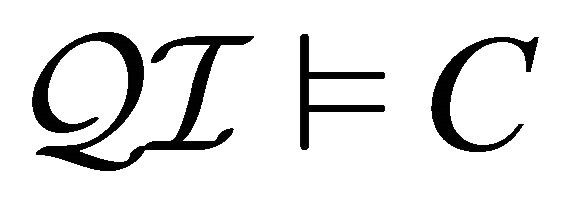 iff
iff . We define a paraconsistent interpretation
. We define a paraconsistent interpretation  by:
by:
1)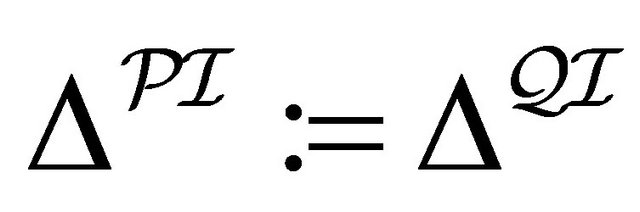 2)
2)  is an interpretation function which assigns to every atomic concept
is an interpretation function which assigns to every atomic concept  a set
a set 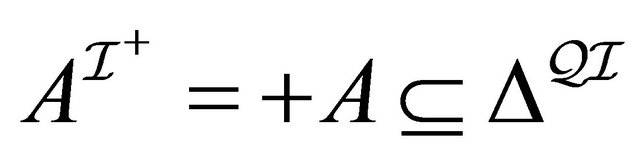 and to every role
and to every role  a binary relation
a binary relation 3)
3)  is an interpretation function which assigns to every atomic concept
is an interpretation function which assigns to every atomic concept  a set
a set 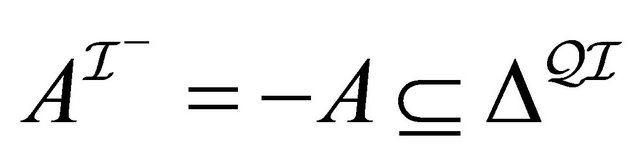 and to every role
and to every role  a binary relation
a binary relation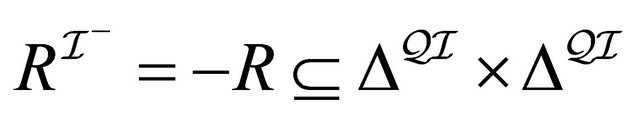 .
.
Then, we have the fact: for any role ,
,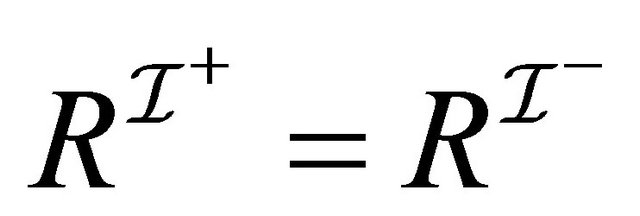 .
.
It is sufficient to show the following claim which implies the required fact. For any concept ,
,
 , (1)
, (1)
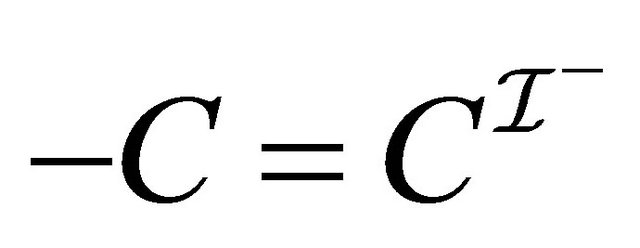 . (2)
. (2)
By (simultaneous) induction on . We show some cases.
. We show some cases.
Case  (
( is an atomic concept): For 1, we have the following by the definition:
is an atomic concept): For 1, we have the following by the definition: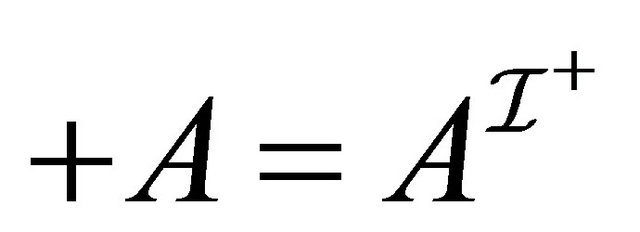 . For 2, we have the following by the definition:
. For 2, we have the following by the definition: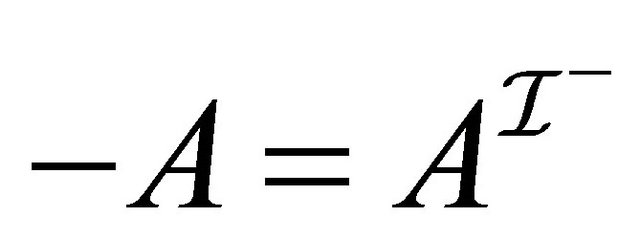 .
.
Case : For 1, we have:
: For 1, we have: 
(by induction hypothesis for 2) . For 2, we have:
. For 2, we have:  (by induction hypothesis for 1)
(by induction hypothesis for 1) .
.
Case : For 1, we have:
: For 1, we have:
 (by induction hypothesis for 1)
(by induction hypothesis for 1)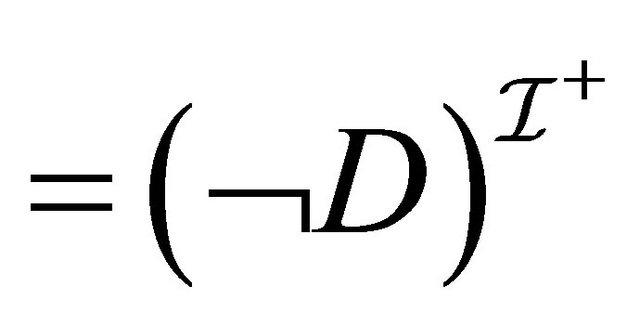 . For 2, we have:
. For 2, we have: 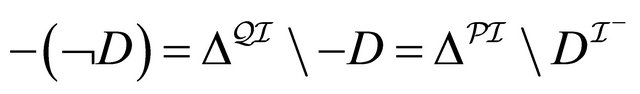 (by induction hypothesis for 2)
(by induction hypothesis for 2) .
.
Case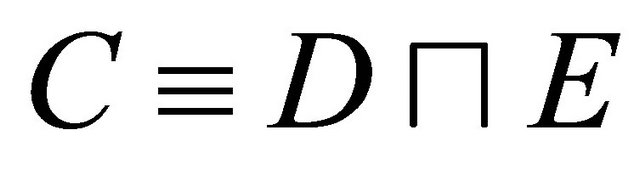 : For 1, we have:
: For 1, we have:  (by induction hypothesis for 1)
(by induction hypothesis for 1)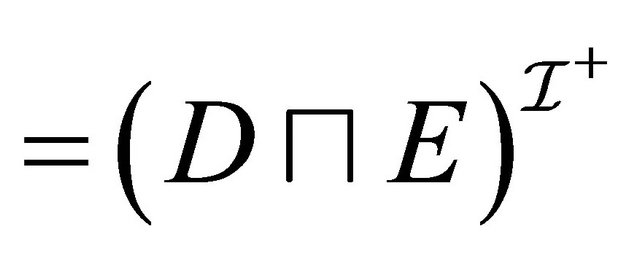 . For 2, we have:
. For 2, we have: 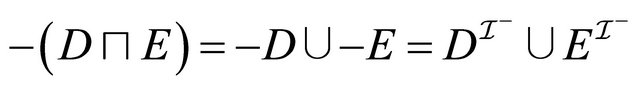 (by induction hypothesis for 2)
(by induction hypothesis for 2) .
.
Case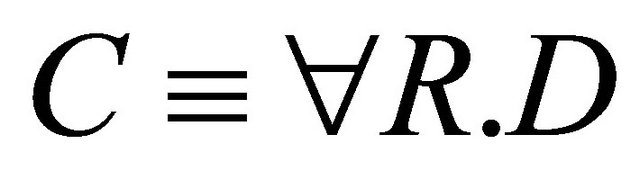 : For 1, we have:
: For 1, we have:
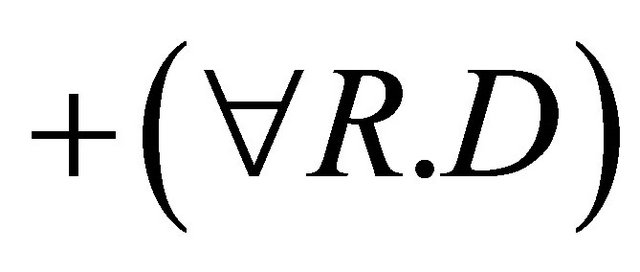

 (by induction hypothesis for 1)
(by induction hypothesis for 1)
 .
.
For 2, we have:
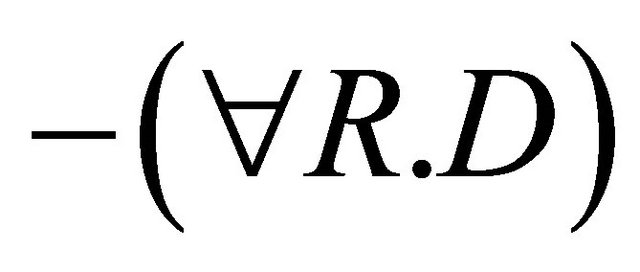
 ,
,
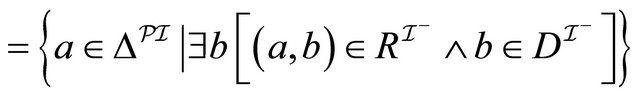 (by induction hypothesis for 2),
(by induction hypothesis for 2),
 .
.

 : Suppose that
: Suppose that  is a paraconsistent interpretation. Then, it is sufficient to construct a quasi-classical interpretation
is a paraconsistent interpretation. Then, it is sufficient to construct a quasi-classical interpretation  such that, for any concept
such that, for any concept ,
, 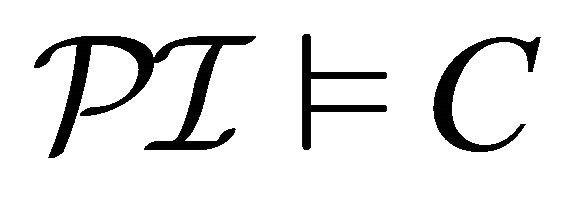 iff
iff . We define a quasi-classical interpretation
. We define a quasi-classical interpretation  by:
by:
1) 2)
2) 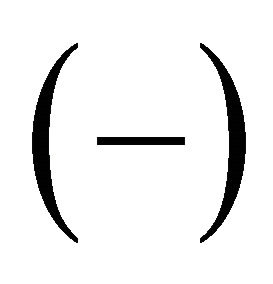
 is a positive (negative, resp.) polarity function which assigns to every atomic concept
is a positive (negative, resp.) polarity function which assigns to every atomic concept  a set
a set 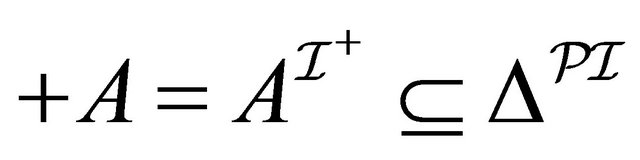 (
( , resp.)3)
, resp.)3)  is an interpretation function which assigns to every atomic concept
is an interpretation function which assigns to every atomic concept  a pair
a pair 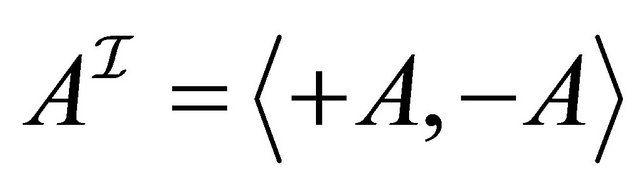 of sets
of sets  and to every role
and to every role  a pair
a pair  of binary relations
of binary relations  .
.
Then, we have the fact: for any role ,
,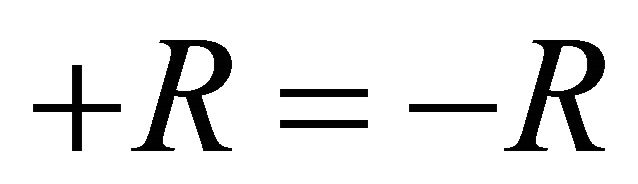 .
.
It is sufficient to show the following claim which implies the required fact. For any concept ,
,
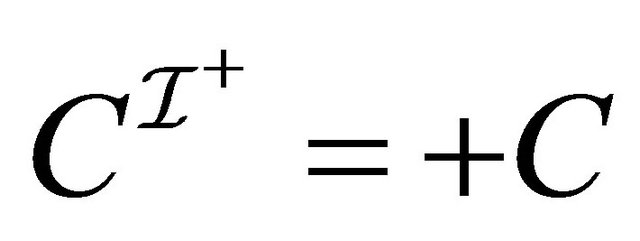 , (1)
, (1)
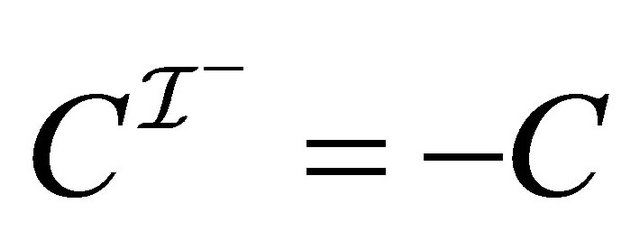 . (2)
. (2)
Since this claim can be shown in the same way as in the claim of the direction , the proof is omitted here. □
, the proof is omitted here. □
3.2.  Semantics
Semantics
We introduce a new logic , which has a singleinterpretation function. The idea of this formulation is inspired from the paraconsistent semantics for a constructive PDL proposed in [8]. These single-interpretation semantics can also be adapted to Nelson’s paraconsistent logic (see [20]).
, which has a singleinterpretation function. The idea of this formulation is inspired from the paraconsistent semantics for a constructive PDL proposed in [8]. These single-interpretation semantics can also be adapted to Nelson’s paraconsistent logic (see [20]).
Similar notions and terminologies for  are also used for
are also used for . The
. The  -concepts are the same as the
-concepts are the same as the  -concepts.
-concepts.
Definition 3.5 Let  be the set of atomic concepts and
be the set of atomic concepts and  be the set
be the set . A single paraconsistent interpretation
. A single paraconsistent interpretation  is a structure
is a structure 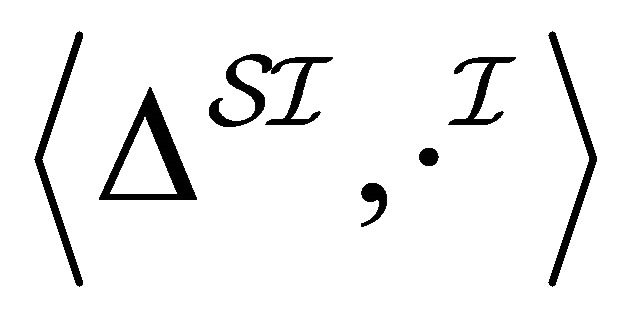 where 1)
where 1)  is a non-empty set2)
is a non-empty set2)  is an interpretation function which assigns to every atomic (or negated atomic) concept
is an interpretation function which assigns to every atomic (or negated atomic) concept  a set
a set  and to every role
and to every role  a binary relation
a binary relation .
.
The interpretation function is extended to concepts by the following inductive definitions:
 , (1)
, (1)
 , (2)
, (2)
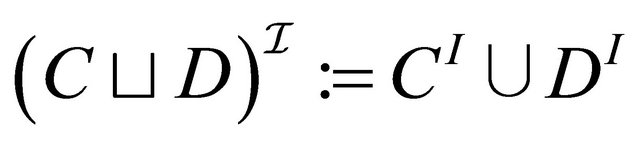 , (3)
, (3)
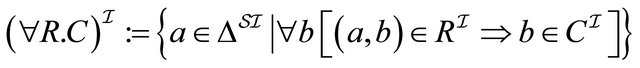 , (4)
, (4)
 , (5)
, (5)
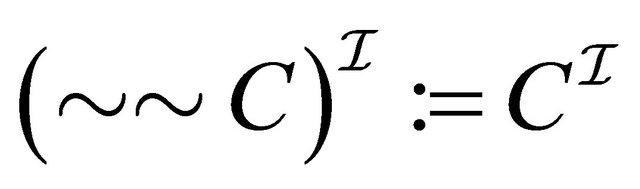 , (6)
, (6)
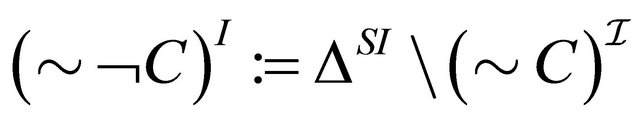 , (7)
, (7)
 , (8)
, (8)
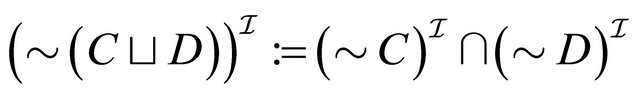 , (9)
, (9)
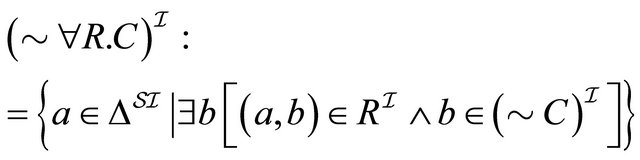 , (10)
, (10)
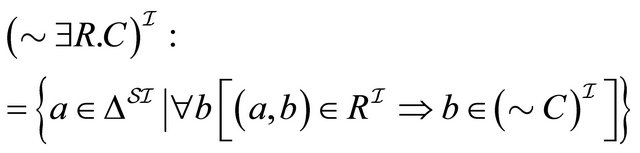 . (11)
. (11)
An expression 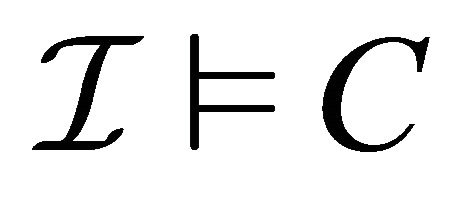 is defined as
is defined as . A single paraconsistent interpretation
. A single paraconsistent interpretation  is a model of a concept
is a model of a concept  (denoted as
(denoted as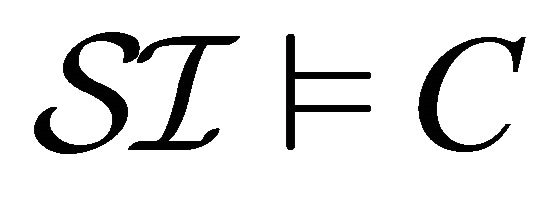 ) if
) if . A concept
. A concept  is said to be satisfiable in
is said to be satisfiable in  if there exists a single paraconsistent interpretation
if there exists a single paraconsistent interpretation  such that
such that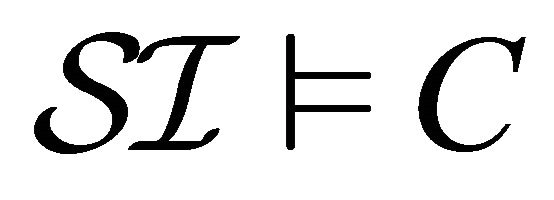 .
.
It is remarked that the logic  in [8] has the same interpretations for A (atomic concept),
in [8] has the same interpretations for A (atomic concept),  (negated atomic concept),
(negated atomic concept),  and
and  as in
as in . Since
. Since 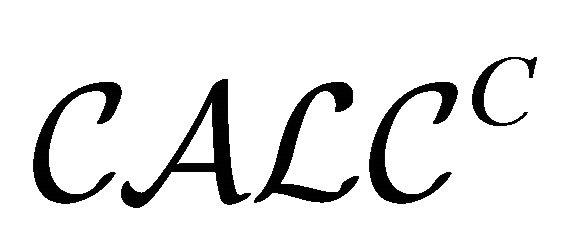 is constructive, it has no classical negation, but has constructive inclusion (constructive implication)
is constructive, it has no classical negation, but has constructive inclusion (constructive implication)  which is defined by:
which is defined by:
 .
.
Next, we show the equivalence between 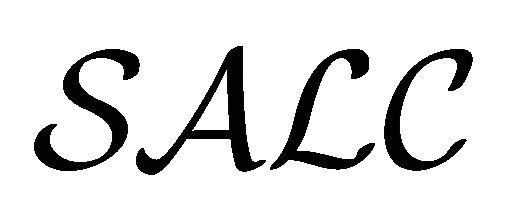 and
and .
.
Theorem 3.6 (Equivalence between 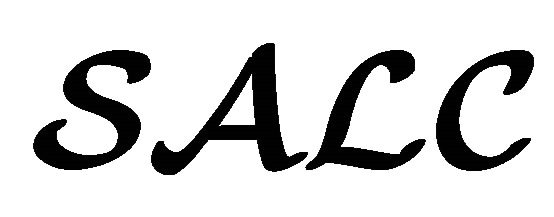 and
and ) For any concept
) For any concept ,
,  is satisfiable in
is satisfiable in  iff
iff  is satisfiable in
is satisfiable in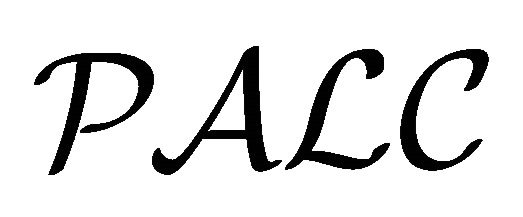 .
.
Proof. Let  be the set of atomic concepts,
be the set of atomic concepts,  be the set
be the set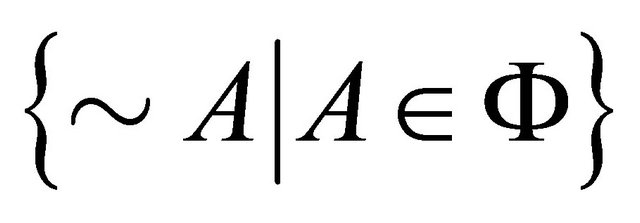 , and
, and  be the set of roles.
be the set of roles.

 : Suppose that
: Suppose that  is a single paraconsistent interpretation such that
is a single paraconsistent interpretation such that 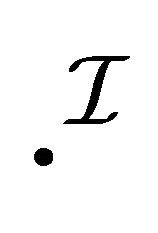 has the domain
has the domain . Then, it is sufficient to construct a paraconsistent interpretation
. Then, it is sufficient to construct a paraconsistent interpretation 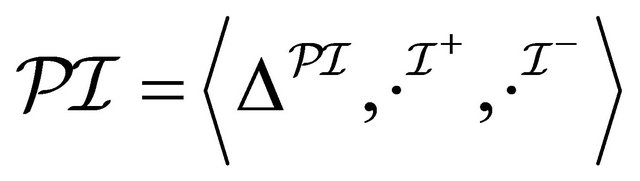 such that, for any concept
such that, for any concept ,
,  iff
iff . We define a paraconsistent interpretation
. We define a paraconsistent interpretation  by:
by:
1)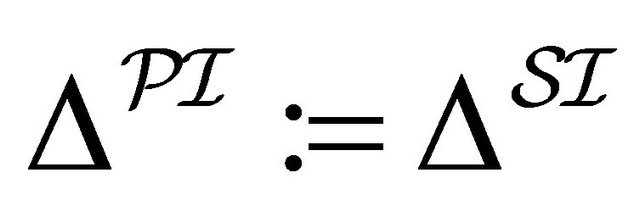 2)
2)  is an interpretation function which assigns to every atomic concept
is an interpretation function which assigns to every atomic concept  a set
a set  and to every role
and to every role  a binary relation
a binary relation 3)
3)  is an interpretation function which assigns to every atomic concept
is an interpretation function which assigns to every atomic concept  a set
a set 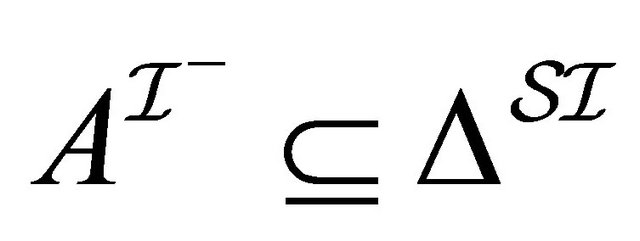 and to every role
and to every role 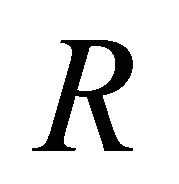 a binary relation
a binary relation 4) for any role
4) for any role ,
,  5) the following conditions hold:
5) the following conditions hold:
 , (a)
, (a)
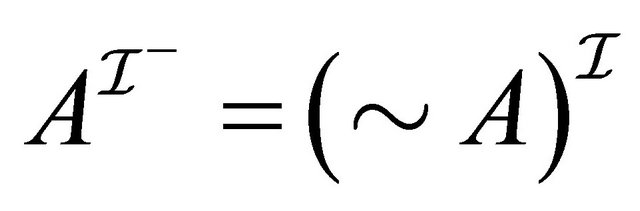 . (b)
. (b)
It is noted that  and
and  have the domain
have the domain .
.
It is sufficient to show the following claim which implies the required fact. For any concept ,
,
 , (1)
, (1)
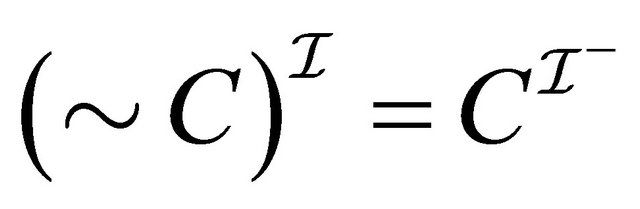 . (2)
. (2)
By (simultaneous) induction on . We show some cases.
. We show some cases.
Case  (
( is an atomic concept): By the definition.
is an atomic concept): By the definition.
Case : For 1, we have:
: For 1, we have:  (by induction hypothesis for 2)
(by induction hypothesis for 2)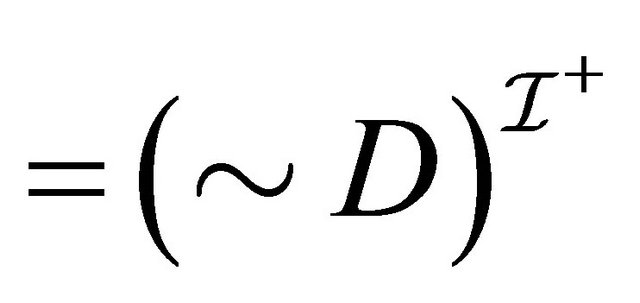 . For 2, we have:
. For 2, we have:  (by induction hypothesis for 1)
(by induction hypothesis for 1) .
.
Case : For 1, we have:
: For 1, we have: 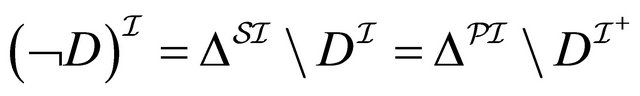 (by induction hypothesis for 1)
(by induction hypothesis for 1) . For 2, we have:
. For 2, we have:  (by induction hypothesis for 2)
(by induction hypothesis for 2)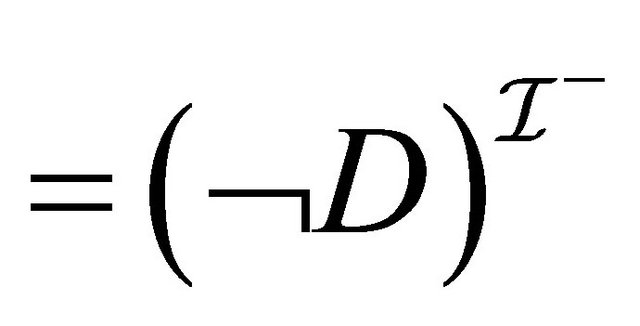 .
.
Case : For 1, we have:
: For 1, we have:  (by induction hypothesis for 1)
(by induction hypothesis for 1) . For 2, we have:
. For 2, we have: 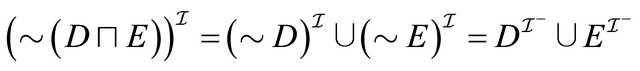 (by induction hypothesis for 2)
(by induction hypothesis for 2) .
.
Case : For 1, we have:
: For 1, we have:
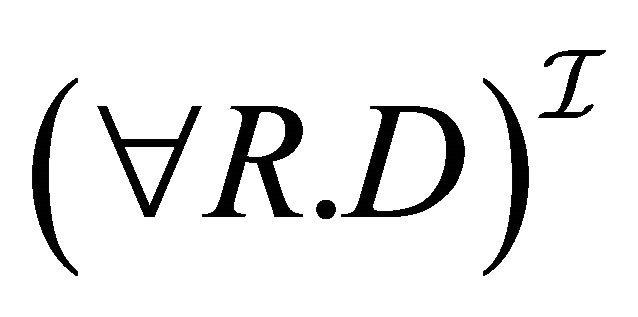
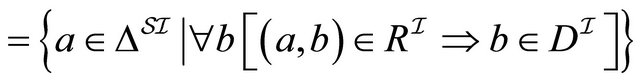
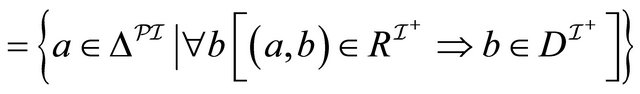 (by induction hypothesis for 1)
(by induction hypothesis for 1)
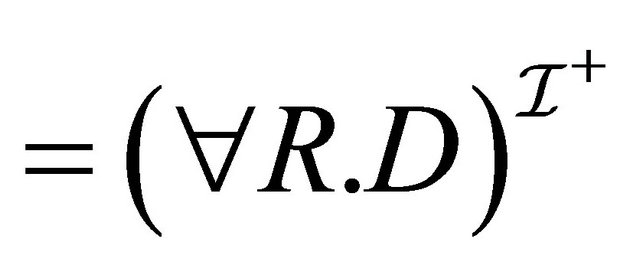 .
.
For 2, we have:
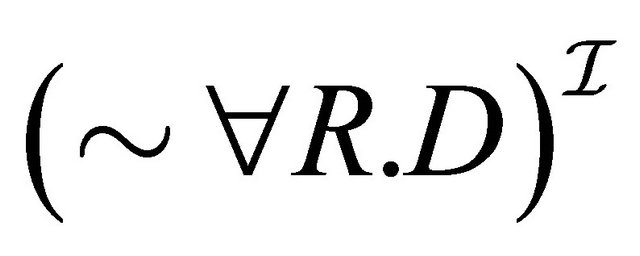
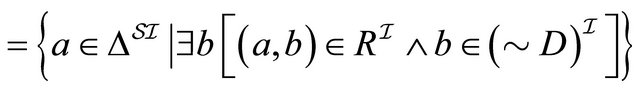 ,
,
 (by induction hypothesis for 2),
(by induction hypothesis for 2),
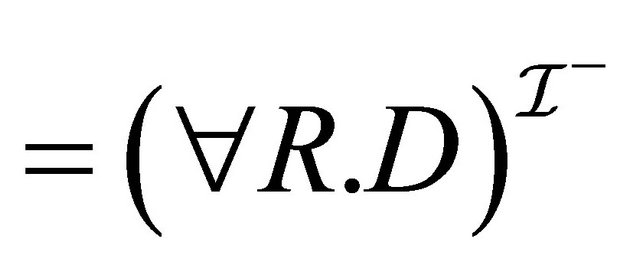 .
.
 : Suppose that
: Suppose that 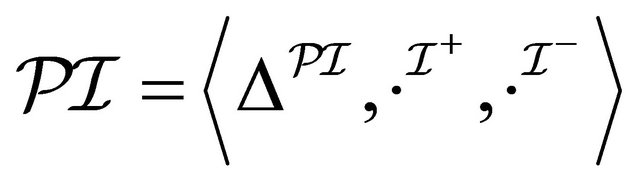 is a paraconsistent interpretation such that
is a paraconsistent interpretation such that  and
and  have the domain
have the domain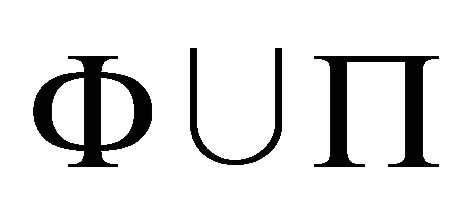 . Then, it is sufficient to construct a single paraconsistent interpretation
. Then, it is sufficient to construct a single paraconsistent interpretation  such that, for any concept
such that, for any concept ,
,  iff
iff . We define a single paraconsistent interpretation
. We define a single paraconsistent interpretation 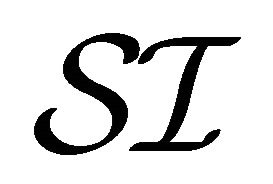 by:
by:
1)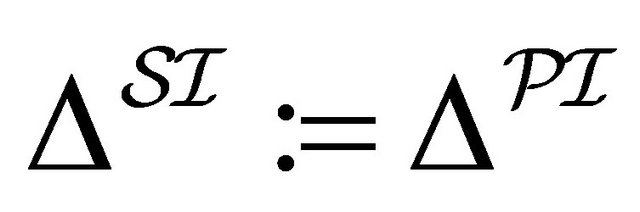 2)
2) 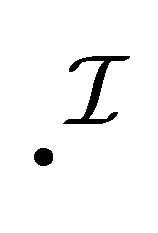 is an interpretation function which assigns to every atomic (or negated atomic) concept
is an interpretation function which assigns to every atomic (or negated atomic) concept 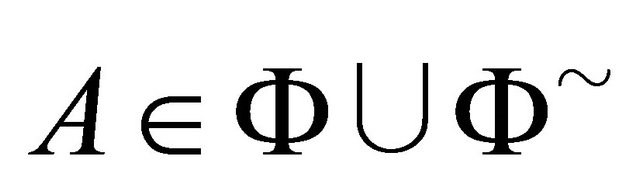 a set
a set  and to every role
and to every role 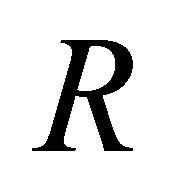 a binary relation
a binary relation 3) the following conditions hold:
3) the following conditions hold:
 , (a)
, (a)
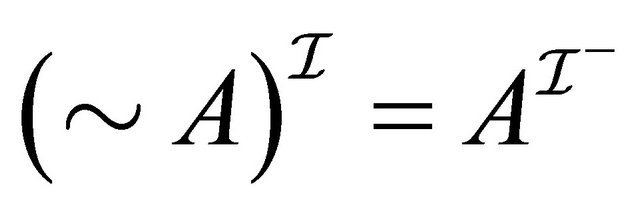 . (b)
. (b)
It is noted that  has the domain
has the domain .
.
It is sufficient to show the following claim which implies the required fact. For any concept ,
,
 , (1)
, (1)
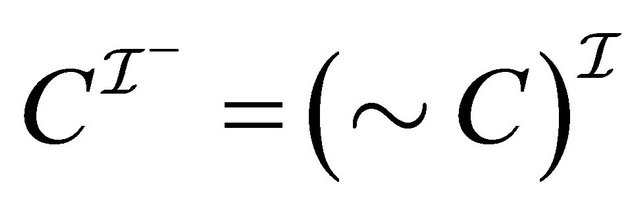 . (2)
. (2)
Since this claim can be shown in the same way as in the claim of the direction , the proof is omitted here. □
, the proof is omitted here. □
4. Remarks
4.1. Constructive Semantics
As mentioned before, three constructive PDLs: ,
, 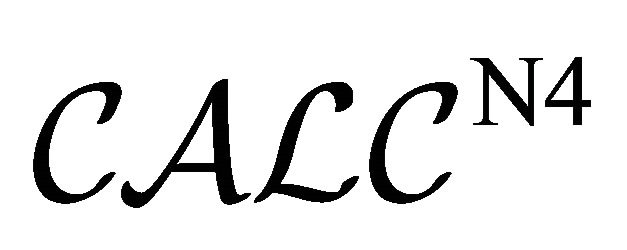 and
and  were introduced and studied in [8,9]. By our comparison results of the present paper, we can consider to present the four-valued semantics, the quasi-classical semantics and the dual-interpretation semantics for these constructive PDLs. The notions of constructiveness and paraconsistency are known to be important for logical systems. From the point of view of the truth and falsehood in a logic, the principle of explosion
were introduced and studied in [8,9]. By our comparison results of the present paper, we can consider to present the four-valued semantics, the quasi-classical semantics and the dual-interpretation semantics for these constructive PDLs. The notions of constructiveness and paraconsistency are known to be important for logical systems. From the point of view of the truth and falsehood in a logic, the principle of explosion  and the excluded middle
and the excluded middle  are the duals of each other. Paraconsistent logics are logics without the principle of explosion, and paracomplete logics are the logics without the excluded middle. Constructive logics are classified as a paracomplete logic. The logics with both the paraconsistency and the paracompleteness are called paranormal (or nonalethic) logics.
are the duals of each other. Paraconsistent logics are logics without the principle of explosion, and paracomplete logics are the logics without the excluded middle. Constructive logics are classified as a paracomplete logic. The logics with both the paraconsistency and the paracompleteness are called paranormal (or nonalethic) logics.
Since the precise definitions of the original semantics for  and
and  are rather complex, we now present only an outline of the (slightly modified versions of the) semantics of
are rather complex, we now present only an outline of the (slightly modified versions of the) semantics of 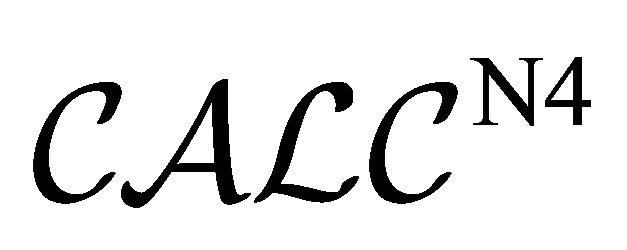 and
and .
.
A constructive interpretation  is a structure
is a structure  where 1)
where 1)  is a non-empty set2)
is a non-empty set2)  is a poset3)
is a poset3) 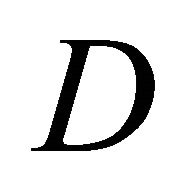 is a domain function from
is a domain function from  to
to 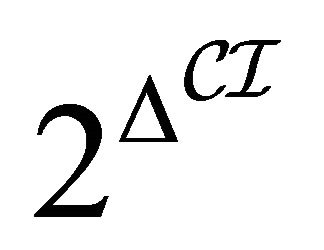 (written ad
(written ad  for
for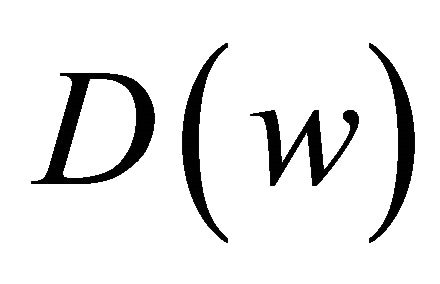 ) such that a) for any
) such that a) for any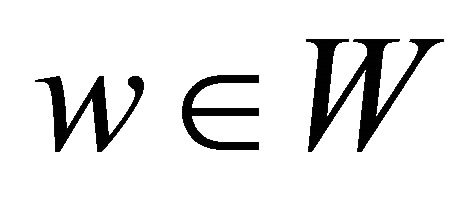 ,
, 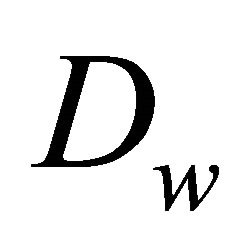 is non-emptyb) for any
is non-emptyb) for any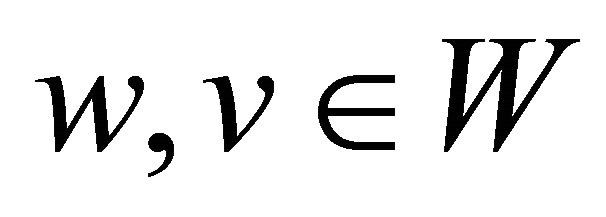 , if
, if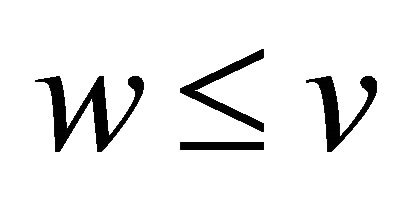 , then
, then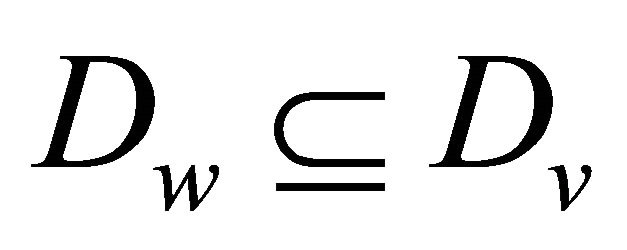 .
.
For each , we interpret an atomic concept
, we interpret an atomic concept  and a negated atomic concept ~A as
and a negated atomic concept ~A as 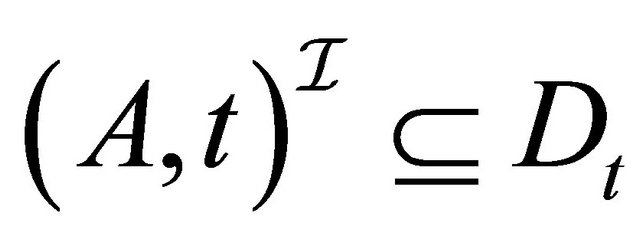 and
and , respectively. Examples of the interpretations of the composite concepts are presented as follows: For each
, respectively. Examples of the interpretations of the composite concepts are presented as follows: For each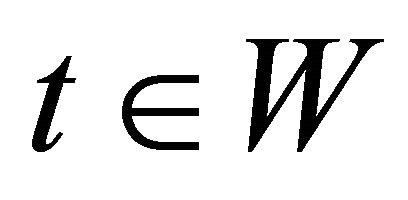 ,
,
 , (1)
, (1)
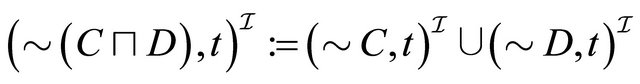 , (2)
, (2)
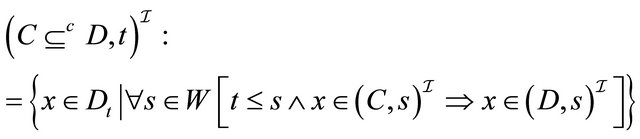 , (3)
, (3)
 . (4)
. (4)
The interpretations of  and
and  are rather complex, and hence omitted here. Such interpretations of
are rather complex, and hence omitted here. Such interpretations of  and
and  imply the differences between the
imply the differences between the  -semantics and the
-semantics and the  -semantics.
-semantics.
4.2. Temporal Semantics
It is remarked that the temporal next-time operator 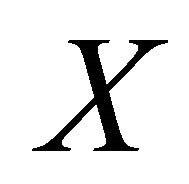 in the temporal description logic
in the temporal description logic 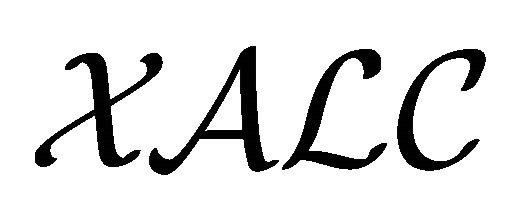 [23] is similar to the paraconsistent negation connective
[23] is similar to the paraconsistent negation connective  in
in . As mentioned, the connective
. As mentioned, the connective  in
in  is from the paraconsistent negation connective in Nelson’s paraconsistent logic N4 [19,20]. The next-time operator
is from the paraconsistent negation connective in Nelson’s paraconsistent logic N4 [19,20]. The next-time operator  in
in 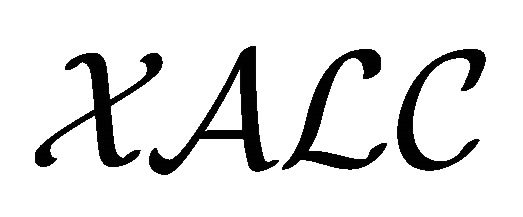 is from Prior’s tomorrow tense logic [24].
is from Prior’s tomorrow tense logic [24].
In the following, we explain 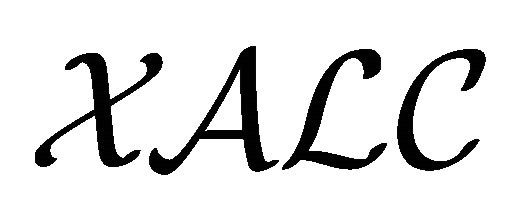 and the similarities between
and the similarities between 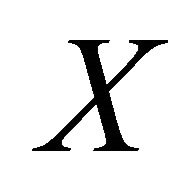 in
in  and
and  in
in .
.
Similar notions and terminologies for 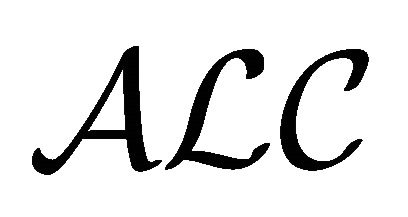 are also used for
are also used for . The symbol
. The symbol  is used to represent the set of natural numbers. The
is used to represent the set of natural numbers. The  -concepts are constructed from the
-concepts are constructed from the 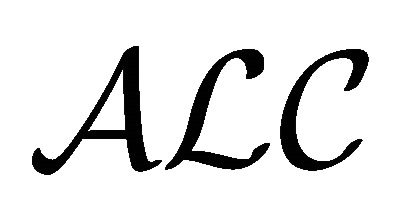 -concepts by adding
-concepts by adding  (next-time operator). An expression
(next-time operator). An expression 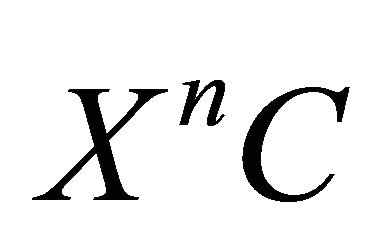 is inductively defined by
is inductively defined by  and
and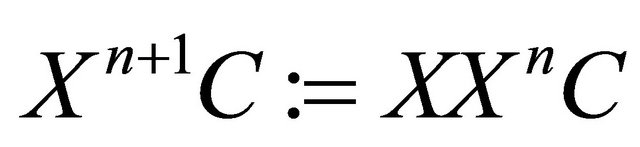 .
.
Definition 4.1 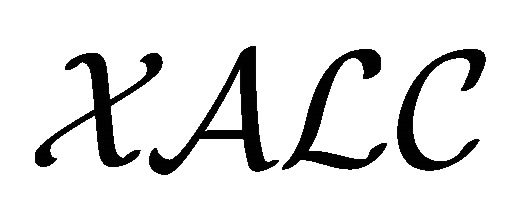 - concepts
- concepts  are defined by the following grammar:
are defined by the following grammar:
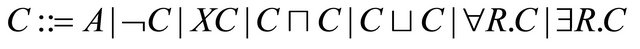
Definition 4.2 A temporal interpretation 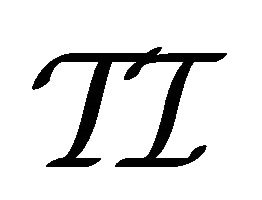 is a structure
is a structure  where 1)
where 1)  is a non-empty set2) each
is a non-empty set2) each 
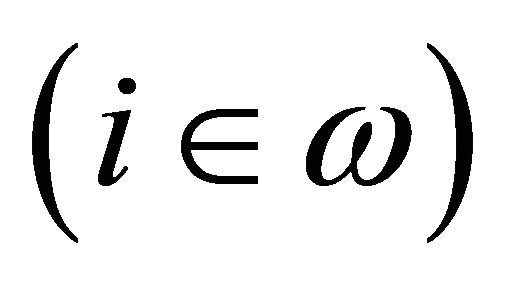 is an interpretation function which assigns to every atomic concept
is an interpretation function which assigns to every atomic concept  a set
a set  and to every role
and to every role  a binary relation
a binary relation 3) for any role
3) for any role  and any
and any ,
,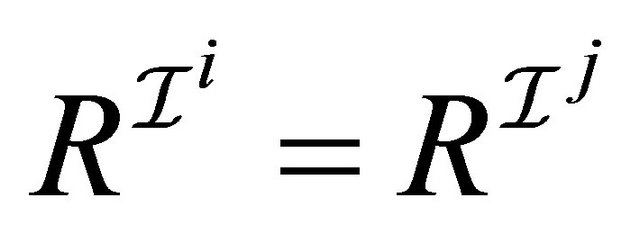 .
.
The interpretation function is extended to concepts by the following inductive definitions:
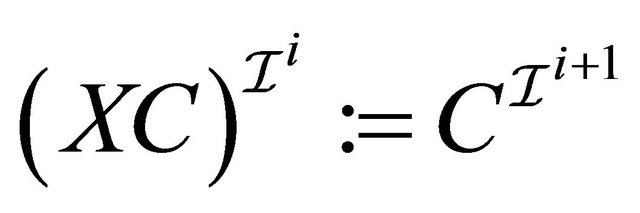 , (1)
, (1)
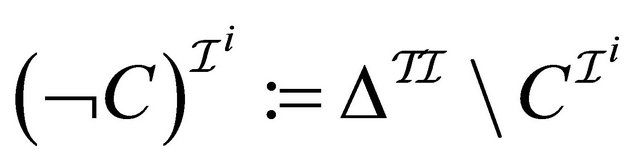 , (2)
, (2)
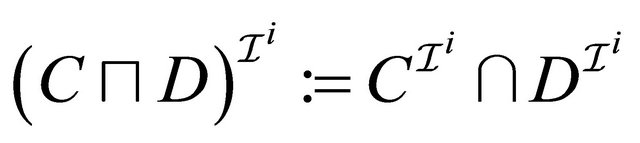 , (3)
, (3)
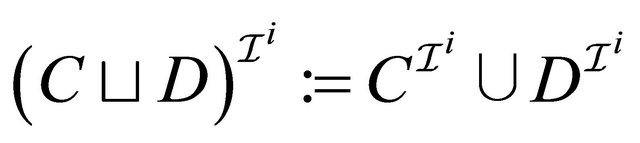 , (4)
, (4)
 , (5)
, (5)
 . (6)
. (6)
For any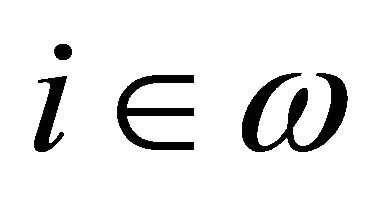 , an expression
, an expression 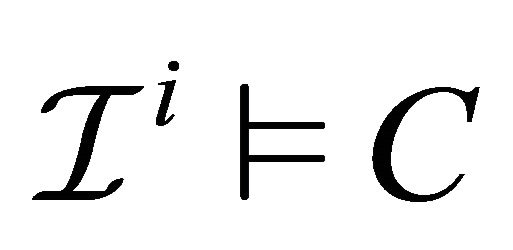 is defined as
is defined as . A temporal interpretation
. A temporal interpretation
 is a model of a concept
is a model of a concept 
(denoted as ) if
) if . A concept
. A concept  is said to be satisfiable in
is said to be satisfiable in  if there exists a temporal interpretation
if there exists a temporal interpretation  such that
such that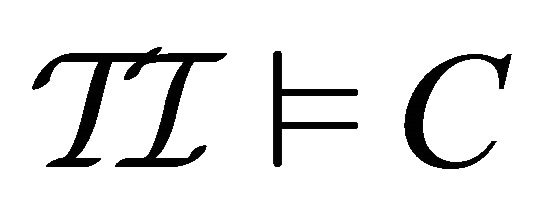 .
.
The interpretation functions  are intended to represent “verification at a time point
are intended to represent “verification at a time point  “.
“.
Intuitively speaking, 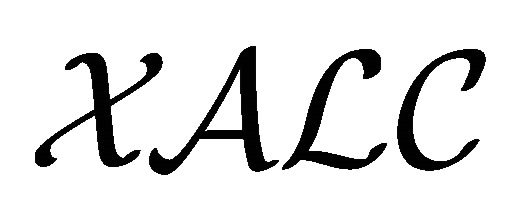 is constructed based on the following additional axiom schemes for
is constructed based on the following additional axiom schemes for :
:
 , (1)
, (1)
 where
where  (2)
(2)
 where
where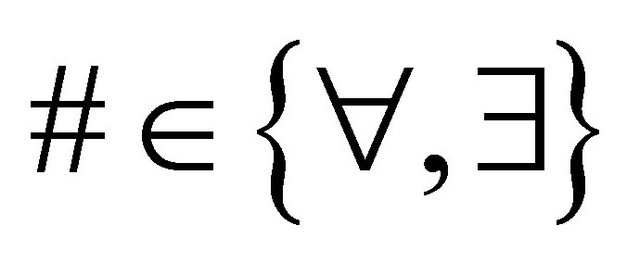 . (3)
. (3)
It is noted that  in
in  and
and  in
in 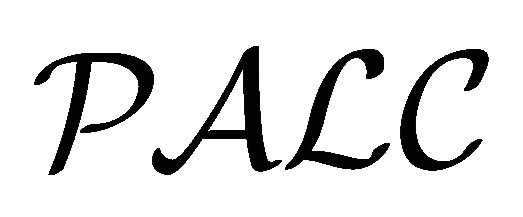 are based on some similar axiom schemes. While
are based on some similar axiom schemes. While  is regarded as a de Morgan type negation connective,
is regarded as a de Morgan type negation connective, 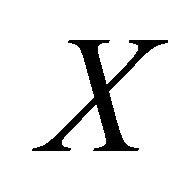 is regarded as a kind of “twisted” de Morgan type connective. By this similarity, we can prove a theorem for embedding
is regarded as a kind of “twisted” de Morgan type connective. By this similarity, we can prove a theorem for embedding 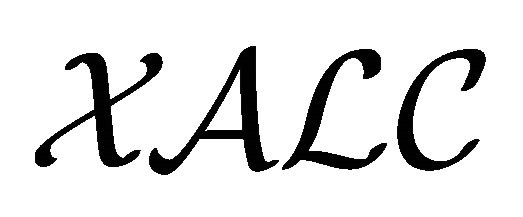 into
into . Such an embedding theorem is similar to a theorem for embedding
. Such an embedding theorem is similar to a theorem for embedding 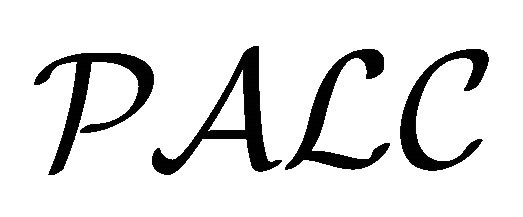 into
into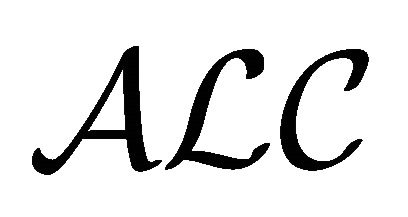 . Thus, in an abstract sense,
. Thus, in an abstract sense, 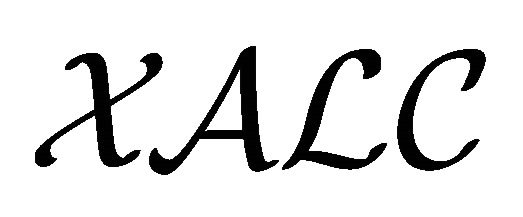 and
and 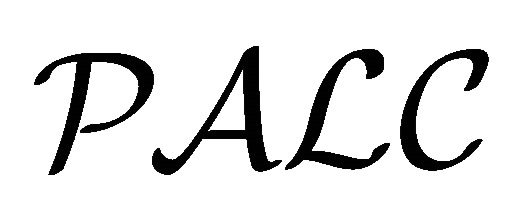 can be viewed as the same kind of embeddable logics. Indeed, the same embedding-based method can be applied to these logics uniformly.
can be viewed as the same kind of embeddable logics. Indeed, the same embedding-based method can be applied to these logics uniformly.
5. Conclusions
In this paper, a comparison of paraconsistent description logics was addressed. New paraconsistent description logics  and
and 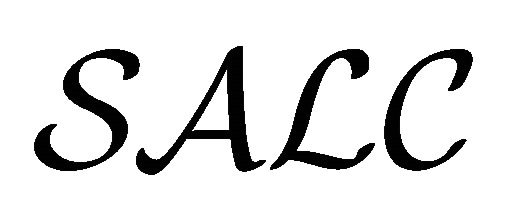 were introduced, and the equivalence among
were introduced, and the equivalence among ,
,  and
and  were proved. The
were proved. The  -semantics is regarded as a generalization of both the four-valued semantics [4,5] and the quasi-classical semantics [12,13]. The
-semantics is regarded as a generalization of both the four-valued semantics [4,5] and the quasi-classical semantics [12,13]. The  -semantics is regarded as a small modification of the singleinterpretation semantics [8,9]. The
-semantics is regarded as a small modification of the singleinterpretation semantics [8,9]. The  -semantics [14], also called dual-interpretation semantics, was taken over from the dual-consequence Kripke-style semantics for Nelson’s paraconsistent logic N4 [18,19].
-semantics [14], also called dual-interpretation semantics, was taken over from the dual-consequence Kripke-style semantics for Nelson’s paraconsistent logic N4 [18,19].
Finally, some recent developments on paraconsistent logics based on N4 are addressed. In [25], proof theory of N4 and its variations were presented. In [26], completeness and cut-elimination theorems were proved for some trilattice logics which are regarded as generalizations of N4. In [27], a paraconsistent linear-time temporal logic was introduced extending the well-known linear-time temporal logic (LTL). In [28], a paraconsistent computation-tree logic was introduced extending the well-known computation-tree logic (CTL). In [29], a constructive temporal paraconsistent logic was introduced combining N4 and a constructive version of LTL.
NOTES
1In [4], the symbol  is used for the paraconsistent negation.
is used for the paraconsistent negation.
2In [12,13], the symbols  and: are used for the paraconsistent negation and the classical negation, respectively.
and: are used for the paraconsistent negation and the classical negation, respectively.