1. Introduction
Let an ellipsoid be given with the three positive semiaxes a, b, c
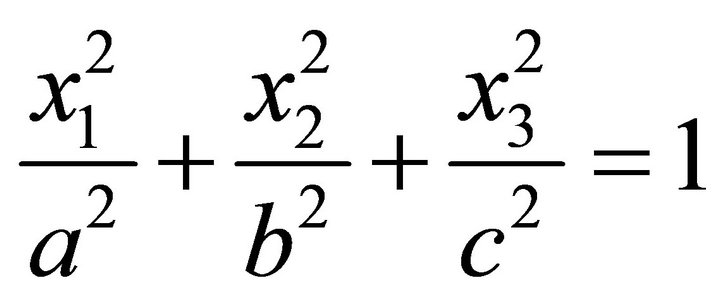 (1)
(1)
and a plane with the unit normal vector

which contains an interior point 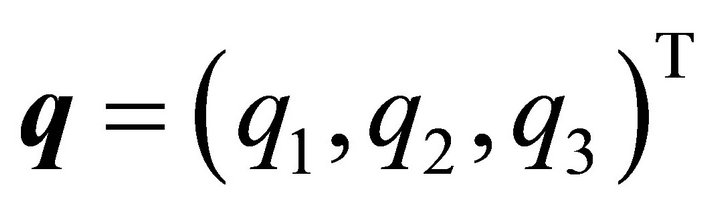 of the ellipsoid. A plane spanned by vectors
of the ellipsoid. A plane spanned by vectors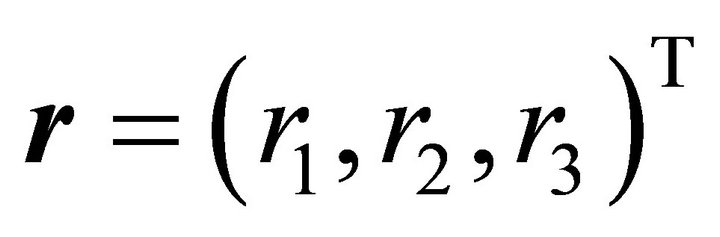 ,
, 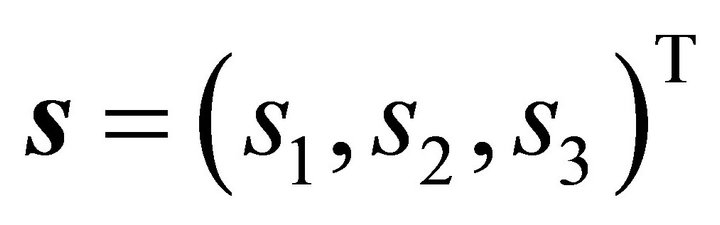 and containing the point
and containing the point  is described in parametric form by
is described in parametric form by
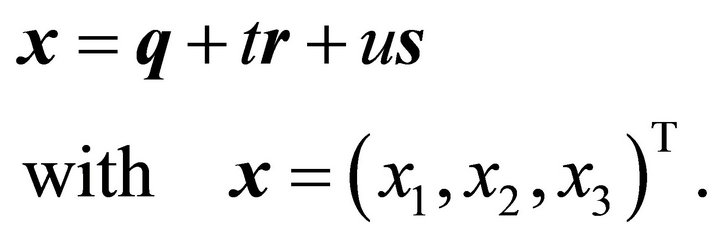 (2)
(2)
Inserting the components of 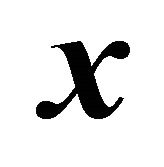 into the equation of the ellipsoid (1) leads to the line of intersection as a quadratic form in the variables
into the equation of the ellipsoid (1) leads to the line of intersection as a quadratic form in the variables  and
and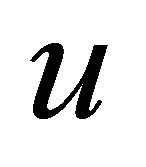 . Let the scalar product in
. Let the scalar product in  for two vectors
for two vectors 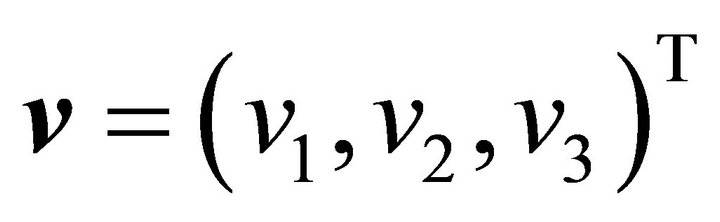 and
and 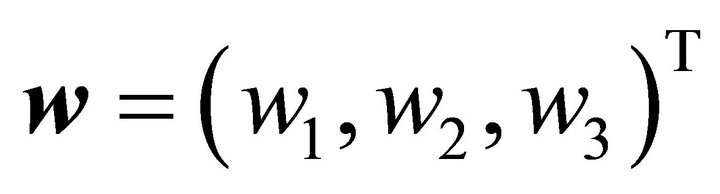 be denoted by
be denoted by

With the diagonal matrix

the line of intersection has the form:
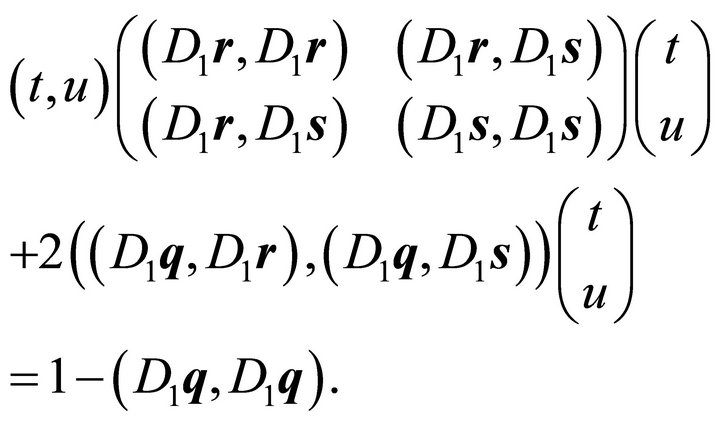 (3)
(3)
As  is an interior point of the ellipsoid the righthand side of Equation (2) is positive. The
is an interior point of the ellipsoid the righthand side of Equation (2) is positive. The 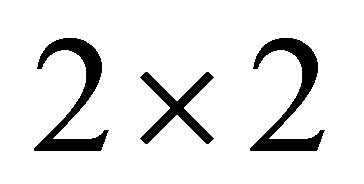 matrix in Equation (3) is a Gram matrix. If the vectors
matrix in Equation (3) is a Gram matrix. If the vectors 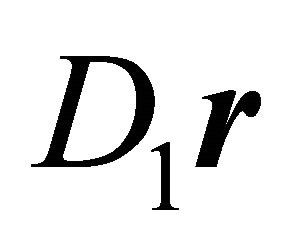 and
and 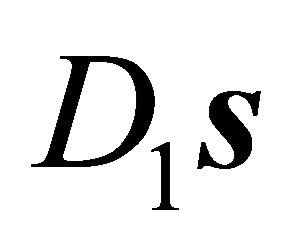 are linearly independent, this is equivalent with the linear independence of the vectors
are linearly independent, this is equivalent with the linear independence of the vectors  and
and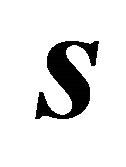 , the matrix in (3) is positive definite and the line of intersection is an ellipse. In [3] a generalization from three to p-dimensional space is discussed.
, the matrix in (3) is positive definite and the line of intersection is an ellipse. In [3] a generalization from three to p-dimensional space is discussed.
Let  and
and 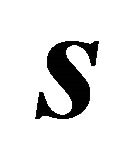 be unit vectors orthogonal to the unit normal vector
be unit vectors orthogonal to the unit normal vector  of the plane
of the plane
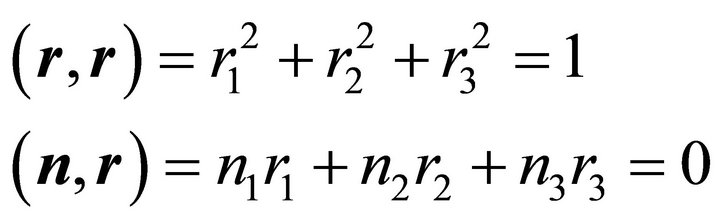 (4)
(4)
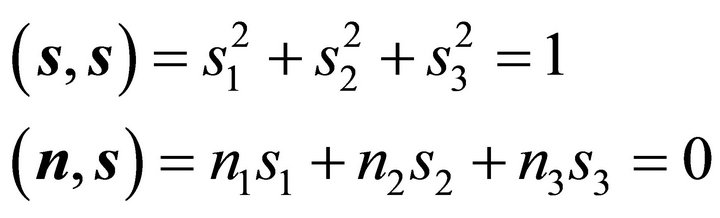 (5)
(5)
and orthogonal to eachother
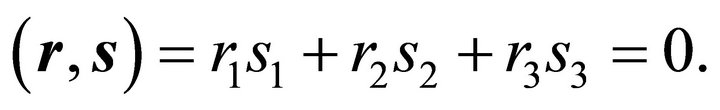 (6)
(6)
Furthermore vectors  and
and  may be chosen such that
may be chosen such that
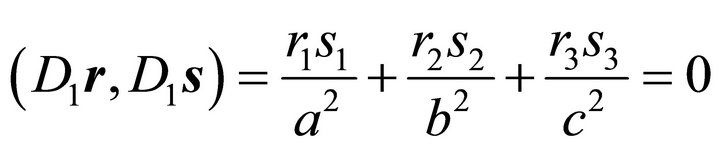 (7)
(7)
holds. This will be shown in the next section. Condition (7) ensures that the  matrix in (3) has diagonal form. Then the line of intersection reduces to an ellipse in translational form
matrix in (3) has diagonal form. Then the line of intersection reduces to an ellipse in translational form
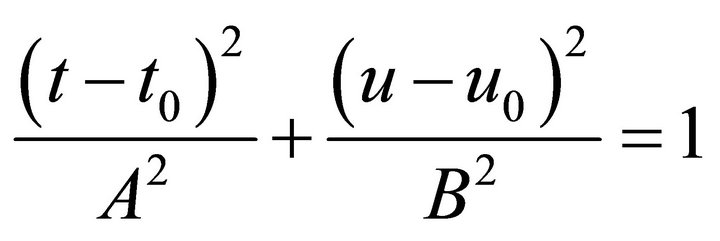 (8)
(8)
with the center 
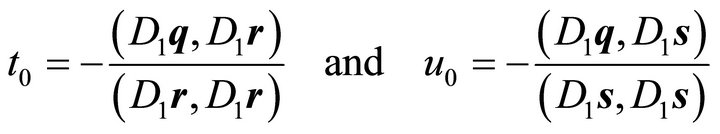 (9)
(9)
and the semi-axes
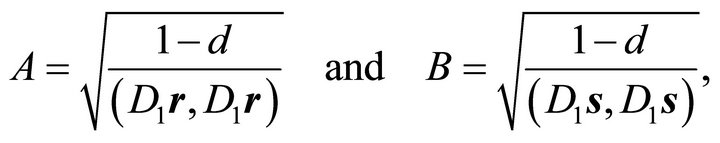 (10)
(10)
where
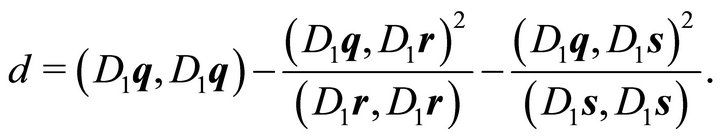 (11)
(11)
In order to show that the semi-axes (10) are independent of the choice of  this vector may be decomposed orthogonally with respect to
this vector may be decomposed orthogonally with respect to :
:
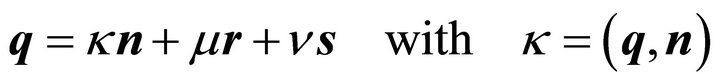 (12)
(12)
where  is the distance of plane (2) from the origin. Substituting
is the distance of plane (2) from the origin. Substituting  into (11) one obtains employing (4), (5), (6) and (7)
into (11) one obtains employing (4), (5), (6) and (7)
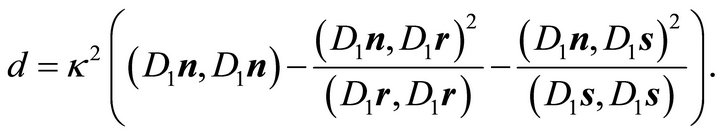 (13)
(13)
The following rules of computation for the cross product in 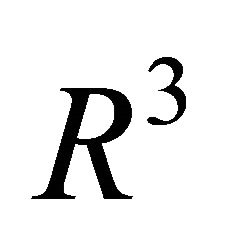 ([4, p.147]) will be applied later on repeatedly. For vectors
([4, p.147]) will be applied later on repeatedly. For vectors  of
of 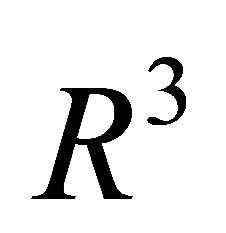 the identity of Lagrange holds
the identity of Lagrange holds
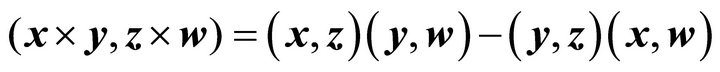 (14)
(14)
and the Grassmann expansion theorem for the double cross product
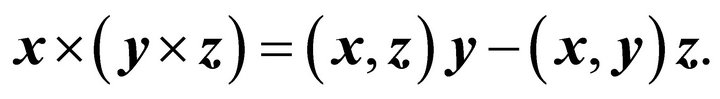 (15)
(15)
2. Construction of Vectors r and s
Let  be a unit vector orthogonal to the unit normal vector
be a unit vector orthogonal to the unit normal vector  of the plane, so that Equations (4) hold. A suitable vector
of the plane, so that Equations (4) hold. A suitable vector 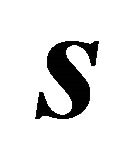 is obtained as a cross product
is obtained as a cross product
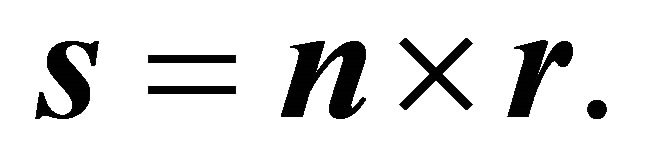 (16)
(16)
Then Equations (5) and (6) are fulfilled: 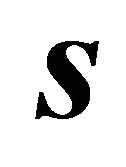 is a unit vector, as can be shown by the identity of Lagrange (14), utilising
is a unit vector, as can be shown by the identity of Lagrange (14), utilising ,
, 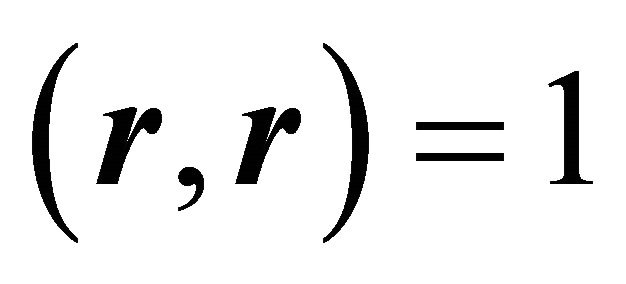 and
and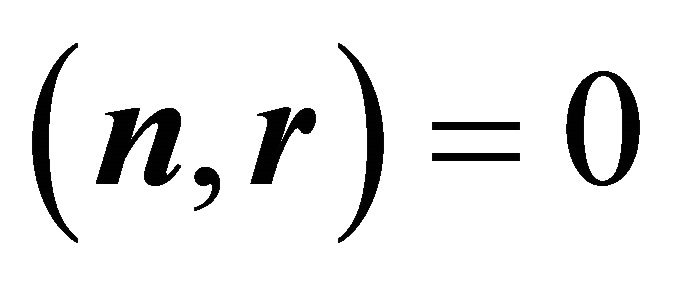 :
:

Furthermore one obtains according to the rules applying to the spar product:


In case Equation (7) is not fulfilled for the initially chosen vectors r and s, i.e.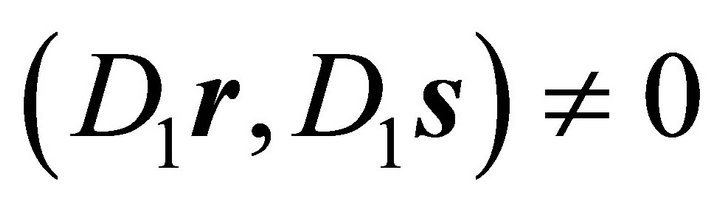 , the following transformation may be performed with
, the following transformation may be performed with 

The transformed vectors  and
and 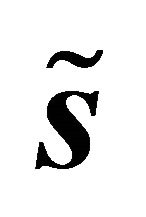 satisfy the following conditions:
satisfy the following conditions: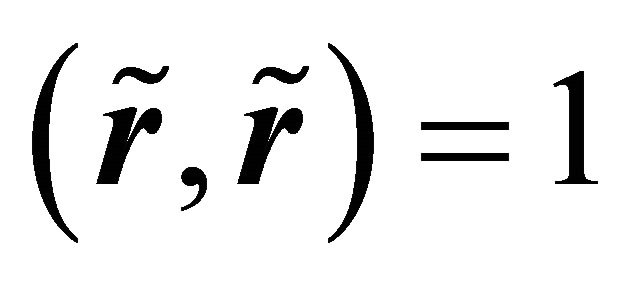 ,
, 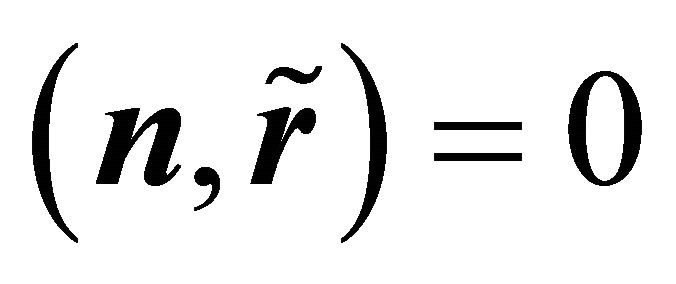 and
and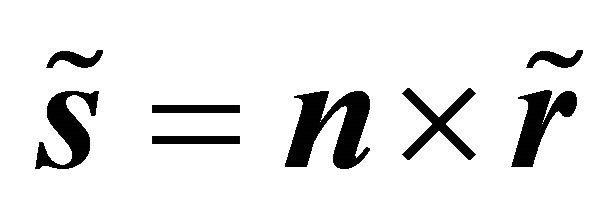 , which imply conditions (4)-(6). The expression
, which imply conditions (4)-(6). The expression

becomes zero, when choosing  such that
such that

holds. This can be reformulated, in case

to

If

holds,  can be chosen
can be chosen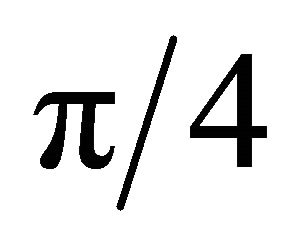 , leading to
, leading to
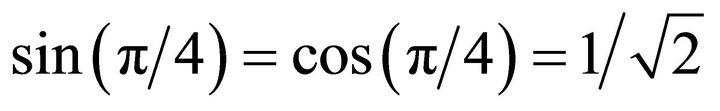 .
.
Corollary 1: For the unit vectors  and
and  orthogonal to each other and
orthogonal to each other and 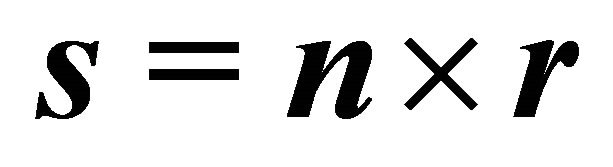 the following statement holds:
the following statement holds:
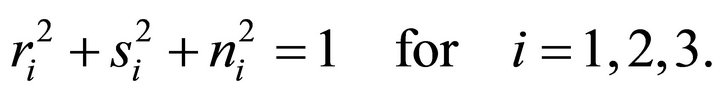 (17)
(17)
Statement (17) follows by substituting the definition of  and utilising
and utilising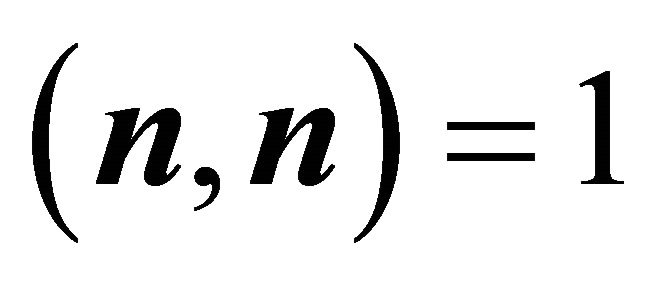 ,
, 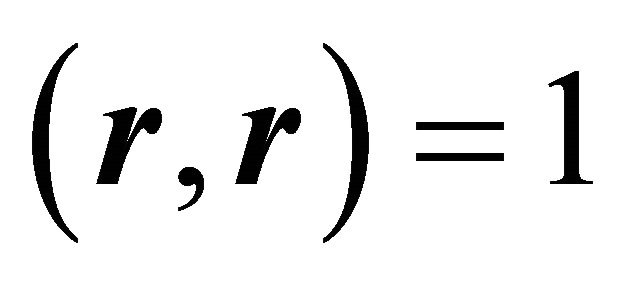 and
and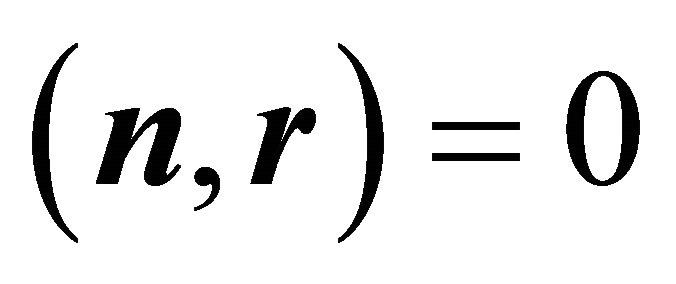 . For
. For 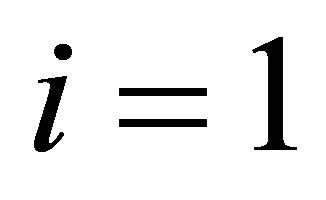 one obtains for instance:
one obtains for instance:

3. A Quadratic Equation
Theorem 1: Let  be the unit normal vector of the plane and let vectors
be the unit normal vector of the plane and let vectors  and
and 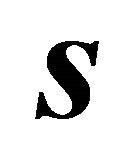 satisfy
satisfy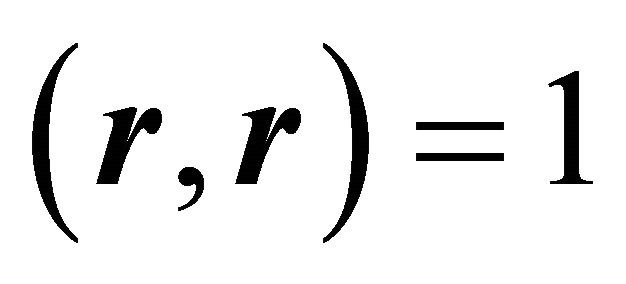 ,
, 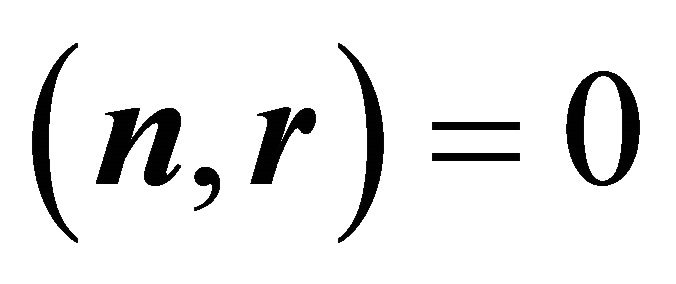 ,
, 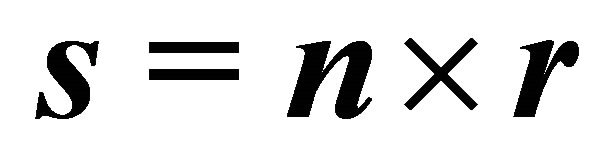 and condition (7). Putting
and condition (7). Putting
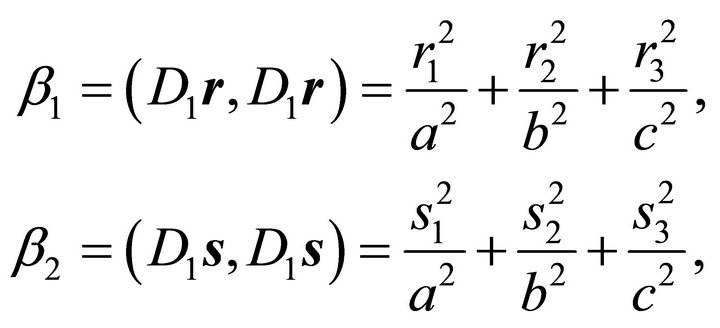 (18)
(18)
 and
and 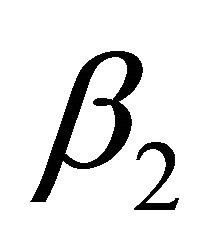 are solutions of the following quadratic equation:
are solutions of the following quadratic equation:
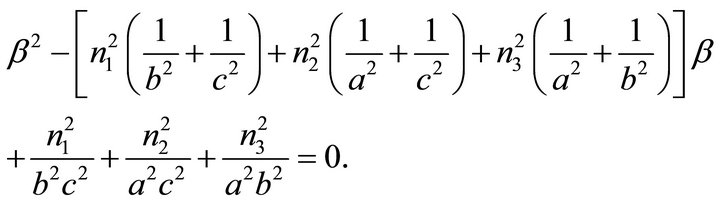 (19)
(19)
Proof: Utilising (17) one obtains:

Applying diagonality condition (7) and the identity of Lagrange (14) leads to:
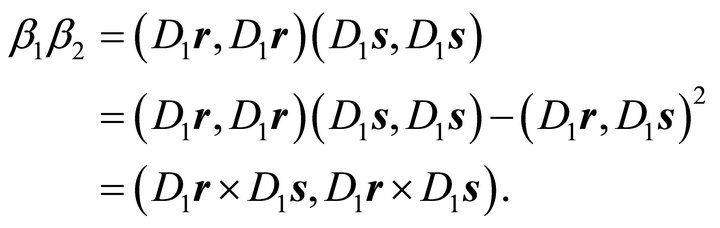 (20)
(20)
For the cross product 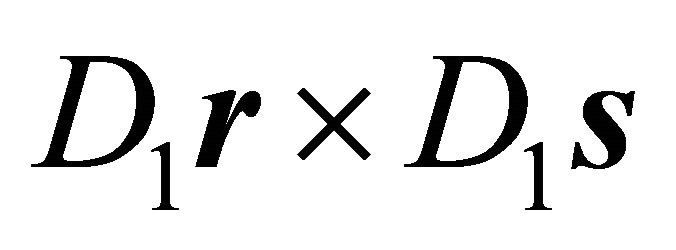 one obtains:
one obtains:
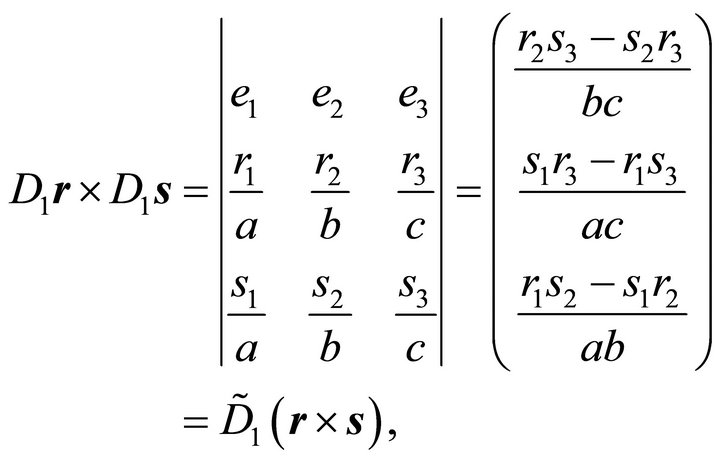 (21)
(21)
with the diagonal matrix
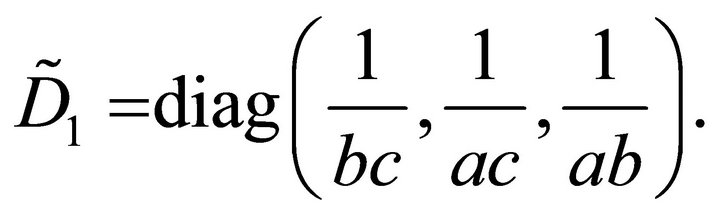 (22)
(22)
According to Grassmann’s expansion theorem for the double cross product (15)
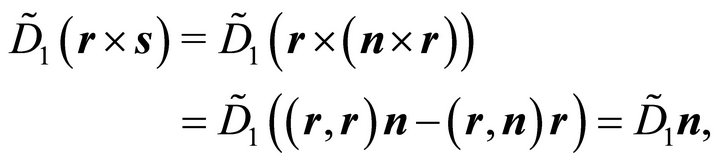 (23)
(23)
follows, since 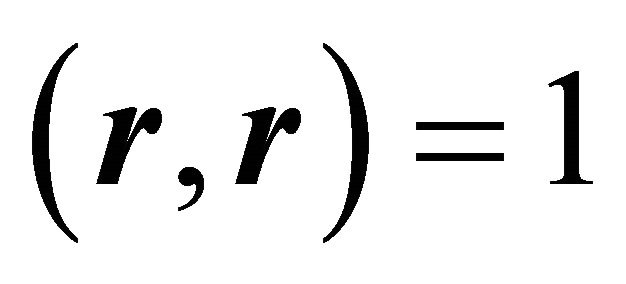 and
and . Applying (20), (21), (23) one obtains:
. Applying (20), (21), (23) one obtains:
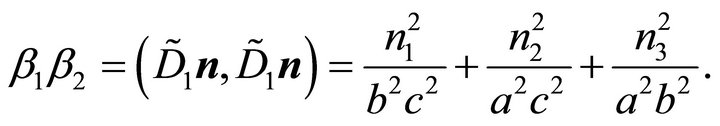 (24)
(24)
□
A quadratic equation equivalent to (19) is considered in [5].
Corollary 2: Under the assumptions of Theorem 1 the following three equations are valid:

The first of the three equations was verified in the proof of Theorem 1. The second and the third equation follow analogously.
4. A Formular for d
Theorem 2: Under the assumptions of Theorem 1 the expression for d in (13) is given by:
 (25)
(25)
where  is taken from (12).
is taken from (12).
Proof: The verification of (25) consists of three steps.
Step 1: Applying the identity of Lagrange (14) the following statements hold:
 (26)
(26)
With Corollary 2 and the diagonal matrix
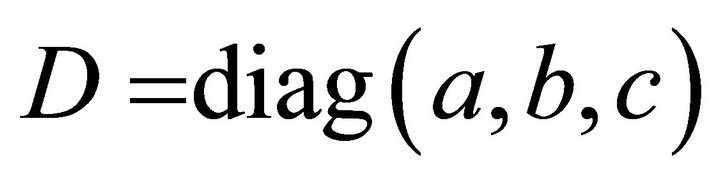 (27)
(27)
one obtains:
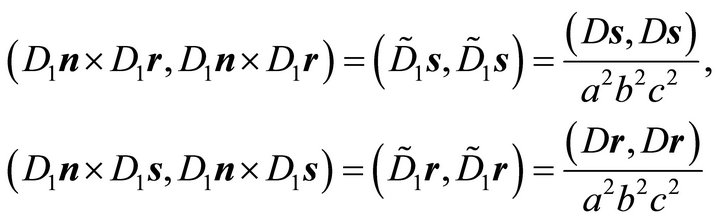 (28)
(28)
and it follows by substituting (28) into (26)
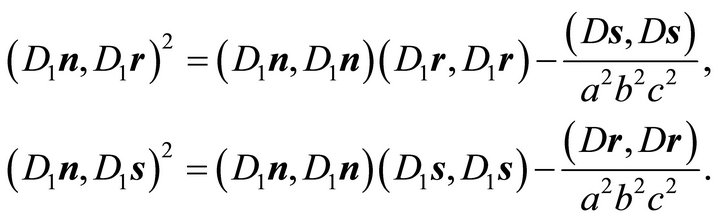 (29)
(29)
Introducing expressions
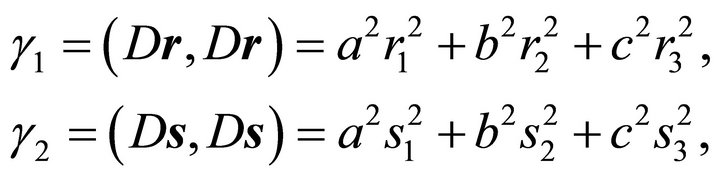 (30)
(30)
one obtains from (29) using (18) and (30)
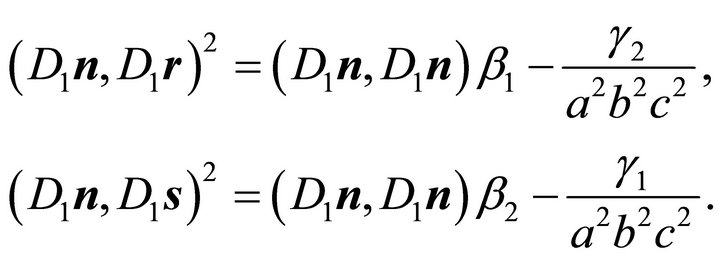 (31)
(31)
Combining both Equations (31) leads to
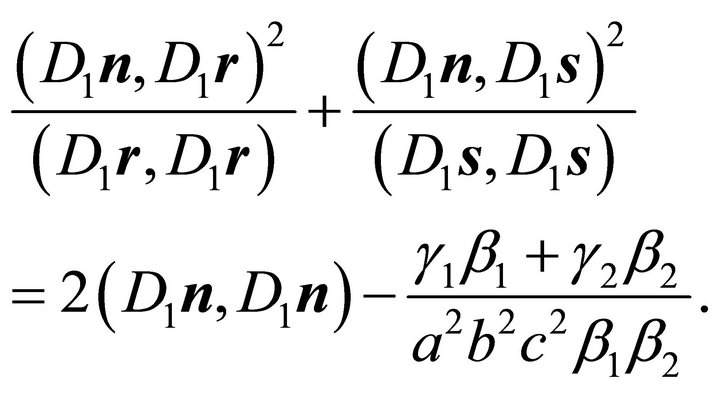 (32)
(32)
Step 2: Analogously to the verification of (24) the application of the identity of Lagrange (14) yields:

With the diagonal matrix 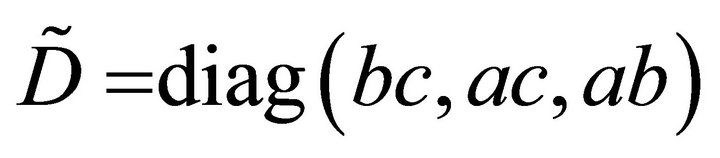 for the cross product
for the cross product  holds:
holds:

Therefore one obtains

or
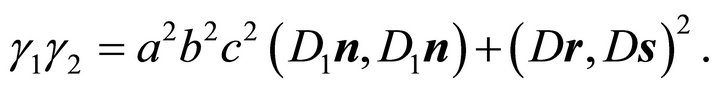 (33)
(33)
In contrast to the verification of (24), where diagonality condition (7) holds, the analogous expression  in (33) need not be zero.
in (33) need not be zero.
Step 3: Applying the identity of Lagrange (14) again leads to

Substituting the involved cross products according to Corollary 2 and considering diagonality condition (7) one obtains

or
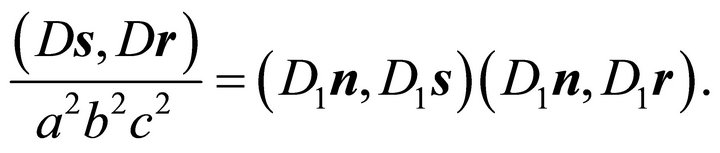 (34)
(34)
Squaring both sides of (34) and substituting the expressions from (31) leads to:

Substitution of (33) results in equation

or
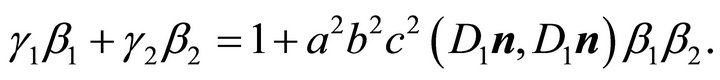 (35)
(35)
Substitution of (35) in (32) leads to:
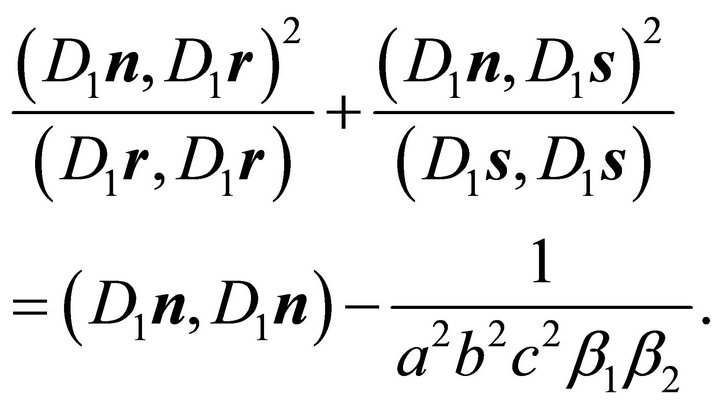 (36)
(36)
Because of (24)
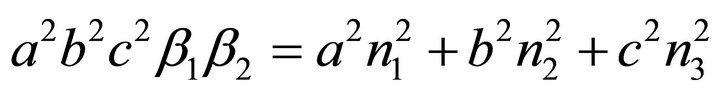 (37)
(37)
holds and with (13) one finally obtains relation (25)

Corollary 3: Under the assumptions of Theorem 1 the area  of the ellipse obtained by the intersection of the ellipsoid (1) and a plane with unit normal vector
of the ellipse obtained by the intersection of the ellipsoid (1) and a plane with unit normal vector  and distance
and distance  from the origin is given by:
from the origin is given by:


This is proven by the formula for the area of an ellipse:

and by applying (25) and (37). The area of intersection  becomes zero in case
becomes zero in case 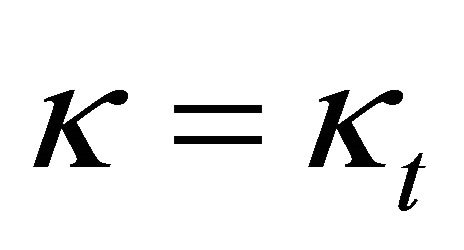 holds; this corresponds to the limiting case, where the cutting plane becomes a tangent plane. This result has been applied in [6].
holds; this corresponds to the limiting case, where the cutting plane becomes a tangent plane. This result has been applied in [6].
5. The Center of the Ellipse
Substituting  according to (12) in formulars (9) for the coordinates
according to (12) in formulars (9) for the coordinates  of the center of the ellipse in the plane spanned by
of the center of the ellipse in the plane spanned by  and
and  one obtains:
one obtains:

and
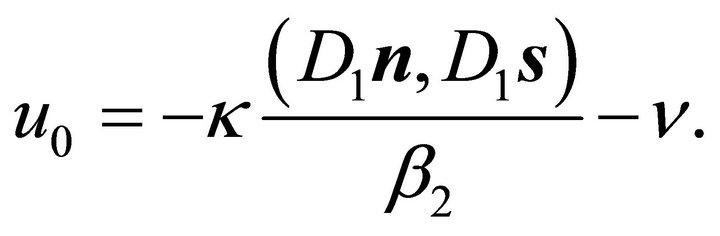 (38)
(38)
The center 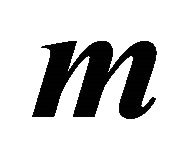 of the ellipse in
of the ellipse in  is given by:
is given by:
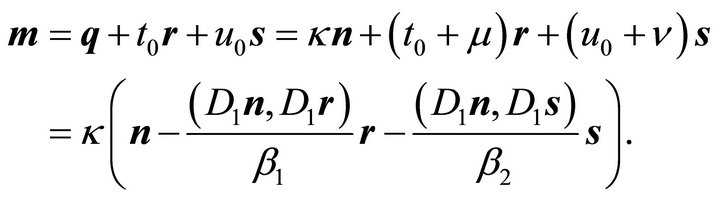 (39)
(39)
Theorem 3: Let the assumptions of Theorem 1 be fulfilled. For the center  of the ellipse of intersection in
of the ellipse of intersection in 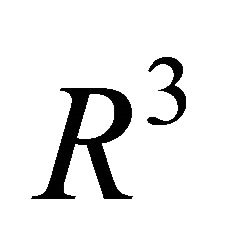 holds:
holds:
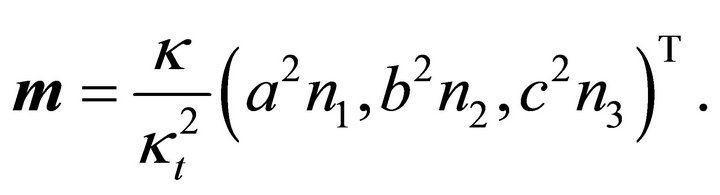 (40)
(40)
Proof: With diagonal matrices 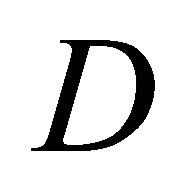 from (27) and
from (27) and 
from (22) utilising 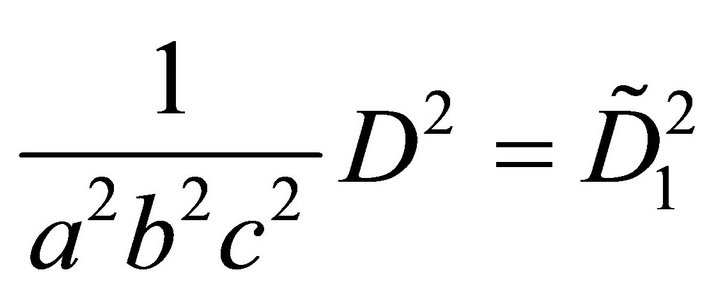 and (37) one obtains a representation of
and (37) one obtains a representation of 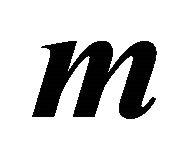 equivalent to (40):
equivalent to (40):
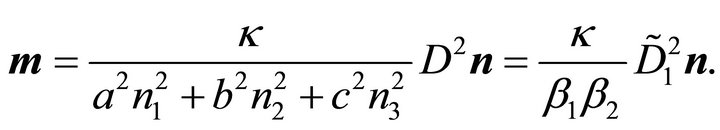 (41)
(41)
It is sufficient to show that for the difference

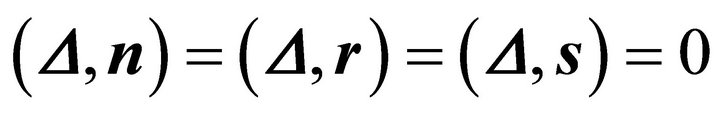 holds. Thus the coefficients in the expansion of
holds. Thus the coefficients in the expansion of  in
in  with respect to the orthonormal basis
with respect to the orthonormal basis 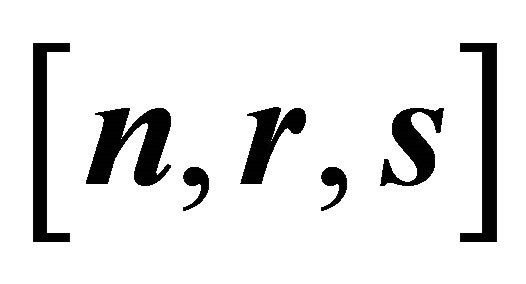 are zero, i.e.,
are zero, i.e.,  is the zero vector.
is the zero vector.
Applying representation (39) one obtains:

The last expression is zero according to (24). Furthermore one obtains:

and by interchanging the roles of  and
and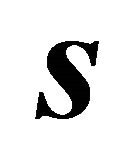 :
:

Both previous expressions are zero; this follows by applying diagonality condition (7), the identity of Lagrange (14) and Corollary 2:

Interchanging the roles of  and
and  leads to:
leads to:

□
Corollary 4: The apexes of the ellipse of intersection are given by

where  and
and 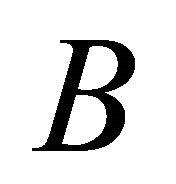 are denoting the semi-axes according to (10).
are denoting the semi-axes according to (10).
Clearly 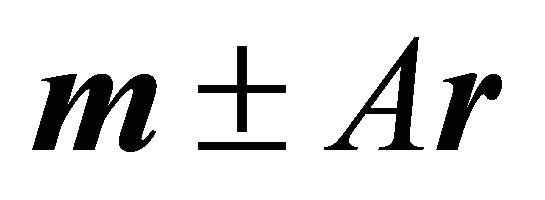 and
and 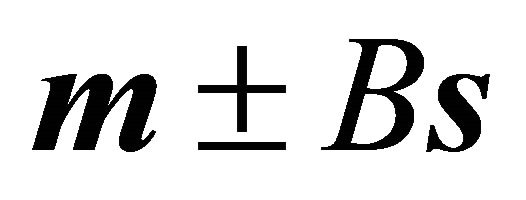 are points of the plane cutting the ellipsoid. In order to show that they are belonging to the ellipse of intersection, it has to be verified that they are situated on the ellipsoid, i.e. the following equalities hold:
are points of the plane cutting the ellipsoid. In order to show that they are belonging to the ellipse of intersection, it has to be verified that they are situated on the ellipsoid, i.e. the following equalities hold:


This can be shown using 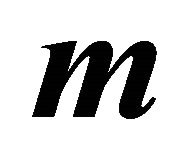 in the form (39) and employing condition (7).
in the form (39) and employing condition (7).
Corollary 5: 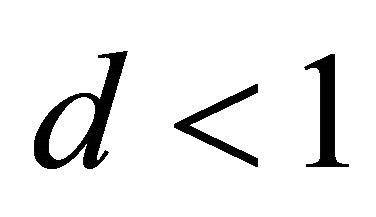 holds if and only if
holds if and only if 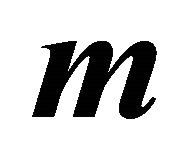 is an interior point of the ellipsoid (1), because of
is an interior point of the ellipsoid (1), because of

In the case of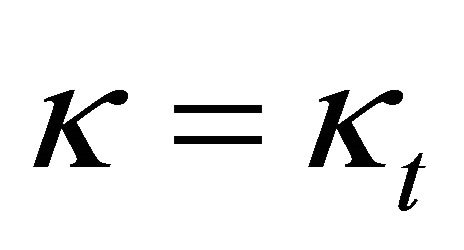 , i.e.
, i.e.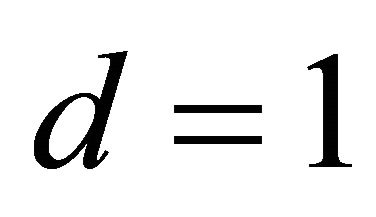 , for the semi-axes (10) of the ellipse of intersection
, for the semi-axes (10) of the ellipse of intersection 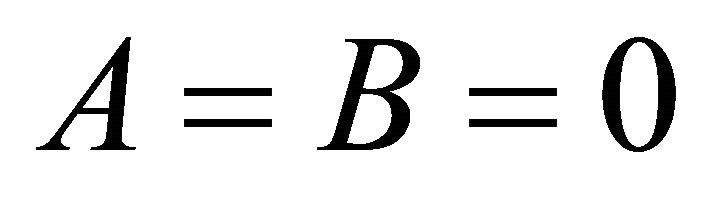 follows. The center (40) of the ellipse of intersection becomes a tangent contact point
follows. The center (40) of the ellipse of intersection becomes a tangent contact point

of ellipsoid (1) and a tangent plane with normal vector , since
, since 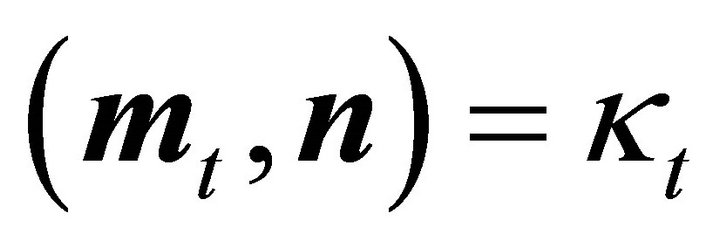 holds.
holds.
Corollary 6: Describing the ellipse of intersection (8) in parametric form


with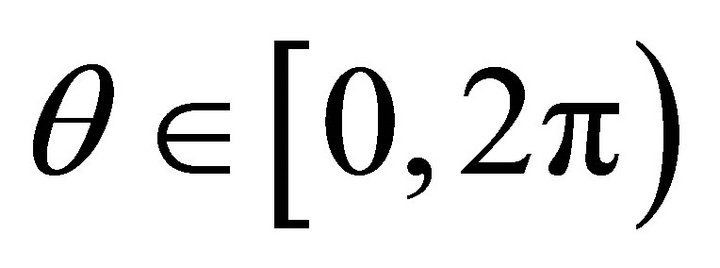 , where
, where  and
and 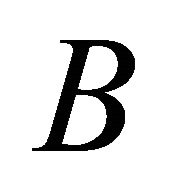 are denoting its semi-axes according to (10), leads to a representation as a curve in three dimensional space as indicated in [7]
are denoting its semi-axes according to (10), leads to a representation as a curve in three dimensional space as indicated in [7]

This result may be derived substituting the parameters  and
and 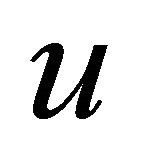 from the parametric form of the ellipse into Equation (2) of the plane:
from the parametric form of the ellipse into Equation (2) of the plane:

or

where 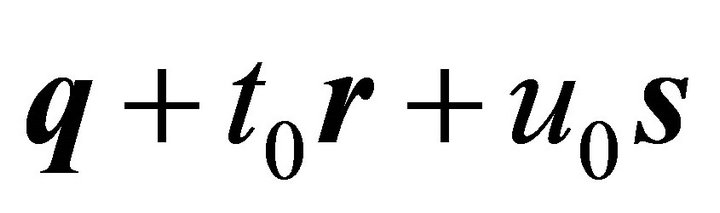 is equal to the center
is equal to the center  of the ellipse as in (39).
of the ellipse as in (39).
6. Applications
As indicated in [2], viewing a section through an ellipsoidal eye from a viewpoint normal to the intersection plane and displaying the intersection on that plane along with a projection of the eye structures and isodose lines, radio-therapy treatment of the eye can be planned. For this purpose the line of intersection of ellipsoid (1) and the plane, having the normal vector 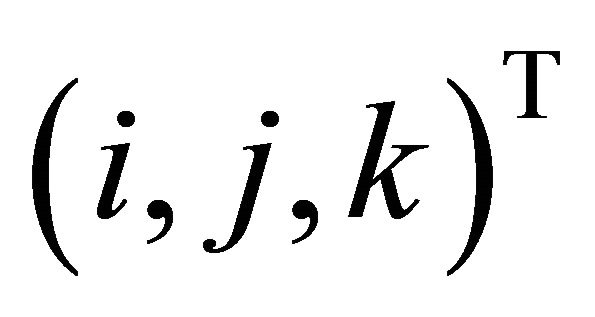 and containing the point
and containing the point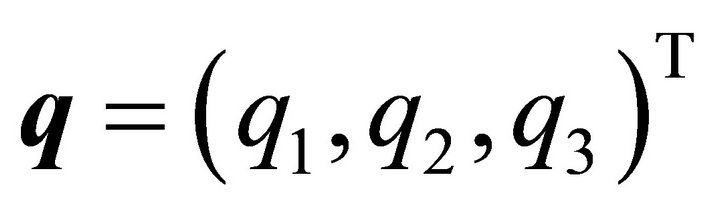 , situated in the interior of (1), is determined. The plane has the form:
, situated in the interior of (1), is determined. The plane has the form:

with the unit normal vector:
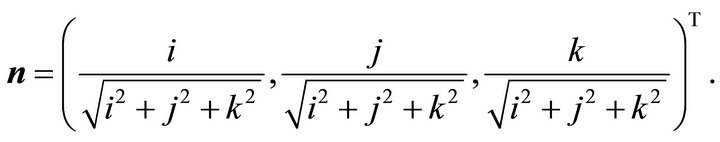 (42)
(42)
The distance of the plane from the origin is given by:
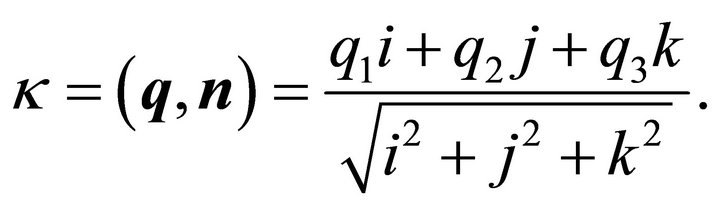 (43)
(43)
According to (25) 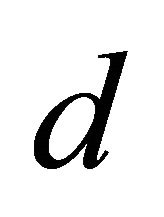 can be written as:
can be written as:
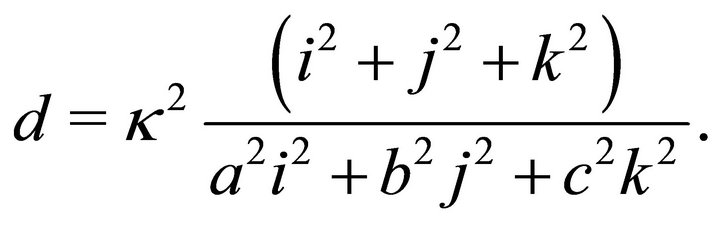 (44)
(44)
From (11) it is obvious that 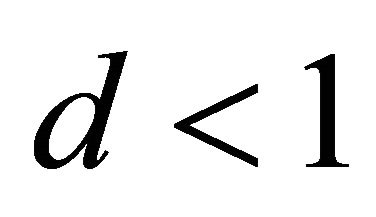 holds, as for
holds, as for  as an interior point of the ellipsoid
as an interior point of the ellipsoid 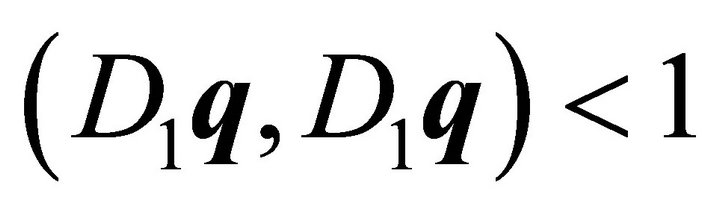 is true. Substituting (18) into (10) the semi-axes of the ellipse, the line of intersection of ellipsoid and plane, are given by
is true. Substituting (18) into (10) the semi-axes of the ellipse, the line of intersection of ellipsoid and plane, are given by
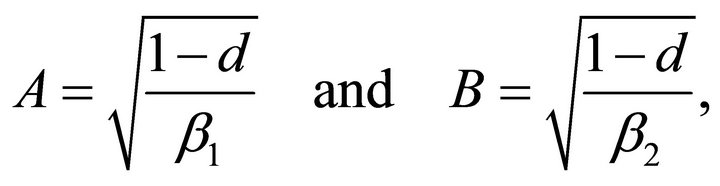 (45)
(45)
where 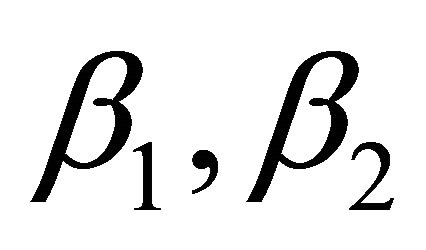 are solutions of Equation (19):
are solutions of Equation (19):
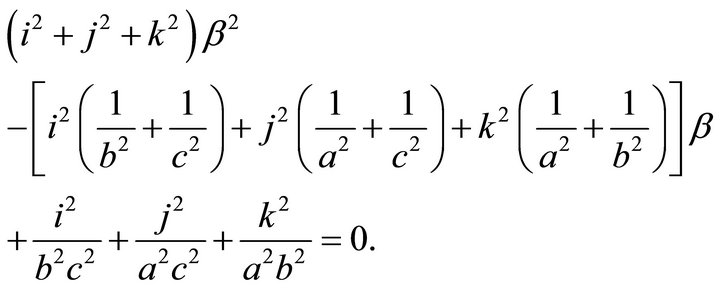 (46)
(46)
With Theorem 3 one obtains by substituting  and
and  from (42) and (43) the formular for the center
from (42) and (43) the formular for the center 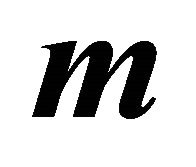 of the ellipse given by:
of the ellipse given by:
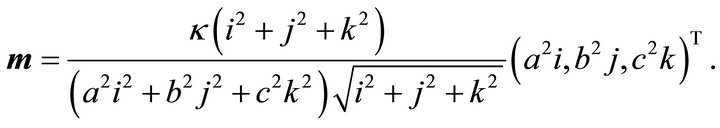 (47)
(47)
Instead of calculating  and
and 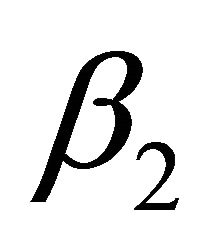 as solutions of (46) they may be obtained alternatively using the procedure described in
as solutions of (46) they may be obtained alternatively using the procedure described in  2. Starting with an arbitrary unit vector
2. Starting with an arbitrary unit vector  orthogonal to the unit normal vector
orthogonal to the unit normal vector  given in (42), e.g.
given in (42), e.g.

calculating 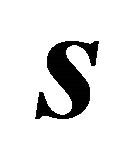 to be orthogonal to both according to
to be orthogonal to both according to  and, in case
and, in case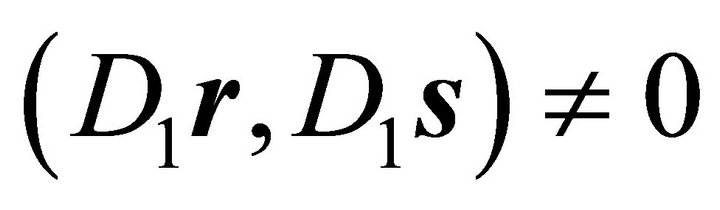 , perform a rotation with angle
, perform a rotation with angle  as described in
as described in  2, yielding new vectors
2, yielding new vectors  and
and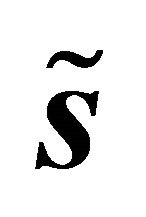 , which are plugged into (18).
, which are plugged into (18).
A Mathematica program containing both ways of computation of  and
and 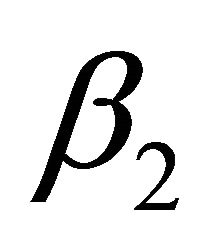 may be obtained from the author upon request.
may be obtained from the author upon request.
In the first special case of a plane containing the origin (see e.g. [1]), i.e.  is the zero vector, it follows by (43), (44) and (47) that
is the zero vector, it follows by (43), (44) and (47) that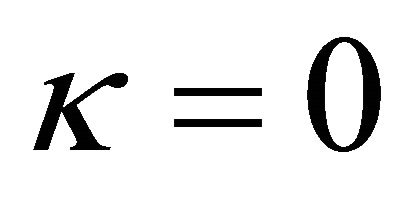 ,
, 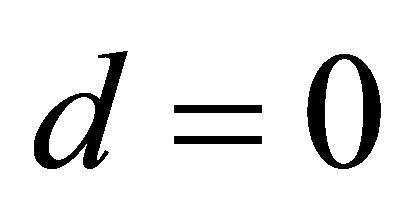 and
and  is the zero vector also. Furthermore the semi-axes of the ellipse in (45) reduce to
is the zero vector also. Furthermore the semi-axes of the ellipse in (45) reduce to

and from (9) 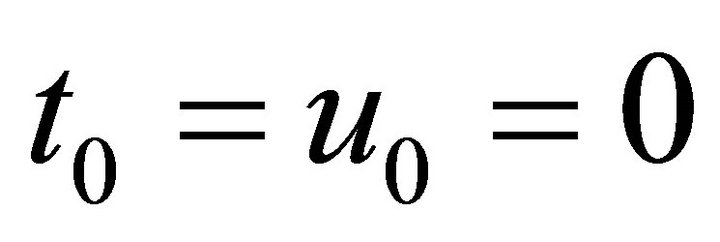 holds. Thus Equation (8) of the line of intersection reduces to
holds. Thus Equation (8) of the line of intersection reduces to

A second special case, where 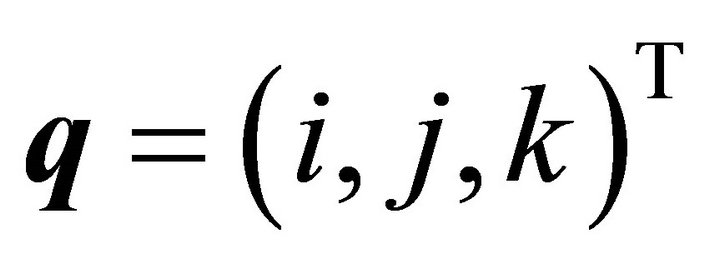 holds, was treated in [2]. Then the above formulas (43), (44) and (47) reduce to:
holds, was treated in [2]. Then the above formulas (43), (44) and (47) reduce to:

and

Because of 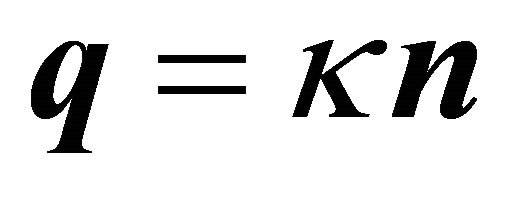 in (12)
in (12) 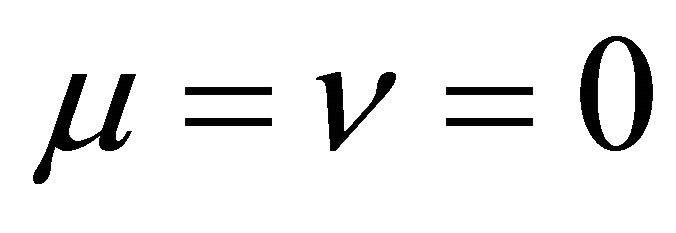 holds and (38) reduces to
holds and (38) reduces to

where  and
and 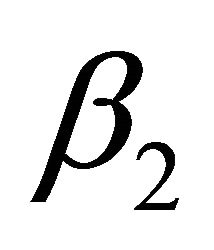 are solutions of the quadratic Equation (46) and vectors
are solutions of the quadratic Equation (46) and vectors  and
and 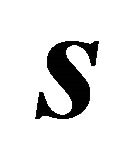 have to be determined as described above according to the procedure shown in
have to be determined as described above according to the procedure shown in  2. Thus Equation (8) of the line of intersection turns into:
2. Thus Equation (8) of the line of intersection turns into:

7. Conclusion
The intention of this paper was, to give an elementary closed form solution to the general problem of the intersection of an ellipsoid and a plane.