On the Existence and Uniqueness of Solutions for Nonlinear System Modeling Three-Dimensional Viscous Stratified Flows ()
1. Introduction
The objective of this paper is to study the qualitative properties of the weak solutions of the system of partial differential equations which describes nonlinear motions of stratified three-dimensional viscous fluid in the gravity field, such as existence, uniqueness and smoothness. This model of three-dimensional stratified fluid corresponds to a stationary distribution of the initial density in a homogeneous gravitational field, which is of Boltzmann type and is exponentially decreasing with the growth of the altitude. The results may be applied in the mathematical fluid dynamics modelling real non-linear flows in the Atmosphere and the Ocean.
The additional unknown function (density), as well as the stratification equation itself, constitutes the novelty of the problem. To construct the solutions, we will use the Galerkin method.
We consider a bounded domain 
with the boundary of the class 
piecewise, and the following system of fluid dynamics
(1.1)
Here 
is the space variable,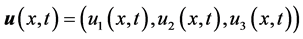 
is the velocity field, 
is the scalar field of the dynamic pressure and 
is the dynamic density. In this model, the stationary distribution of density is described by the function
, where N is a positive constant. The gravitational constant g and the viscosity coefficient 
are also assumed as strictly positive.
For linear non-viscous case, Equations (1.1) are deduced, for example, in [1] -[3] . For linear viscous compressible fluid, system 1.1 is deduced, for example, in [4] . The linear system corresponding to 1.1, was studied from various points of view, and some results may be found in [5] -[10] .
There exists, of course, huge bibliography concerning Navier-Stokes system (see, for example, [11] -[14] ).
However, the non-linear system modelling stratified viscous flows have not been studied mathematically yet, and thus our research was motivated by the novelty of the presence of the term 
in the third equation of 1.1, and also by the presence of the fourth equation itself.
2. Construction and Existence of a Weak Solution
We denote 
and observe that, without loss of generality we can consider
. In this way, we write Equations (1.1) in the vector form:
(1.2)
We associate system 1.2 with the initial conditions
(1.3)
and the Dirichlet boundary conditions
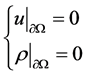. (1.4)
Let 
be a functional space of smooth solenoidal functions with compact support in Ω. We denote as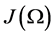 
the closure of 
in the norm
. We also denote as 
the space of solenoidal functions from 
which satisfy homogeneous Dirichlet condition.
Definition 1.
Let
,
.
For any pair of vector functions 
we denote
.
We will call 
a weak solution of 1.2-1.4, if the following integral identities hold
(1.5)
(1.6)
for every pair of functions 
such that
, 
, and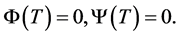 
We observe that the relations 1.5 - 1.6 are obtained in a natural way after multiplying by 
the system 1.2, and integrating by parts over 
for x and over the interval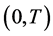 
for t. After knowing the functions
, the function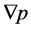 
can be easily found from 1.2.
Let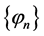 
be a complete orthonormal system in
. We observe that, without loss of generality, it can be chosen as a system of eigenfunctions of Stokes operator (see, for example, [11] [13] [15] ).
We construct the solutions of 1.2 as Galerkin approximations
(1.7)
where 
are unknown coefficients and 
are obtained as solutions of Cauchy problem
(1.8)
Our primary aim is to determine the existence of 
and the resulting properties of the approximations
.
If we consider 1.5 for 
and
then, the arbitrary election of 
will imply the relations
(1.9)
We transform now the system 1.9 into an autonomous system of differential equations of the first order with respect to the variables
, where the vector field is
. If we denote
, then it can be easily seen that the system 1.9 is equivalent to
, (1.10)
where
,
,
.
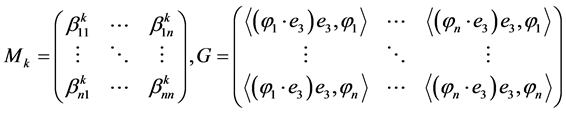After differentiating 1.10, we obtain
, (1.11)
where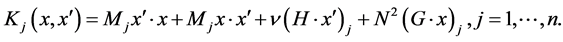 
We introduce the notation 
and thus rewrite 1.11 as
. (1.12)
Since 
is an infinitely differentiable vector field, then, from the theory of ordinary differential equations, we conclude that 1.12 admits a maximal solution in the interval
.
Now, we shall deduce some estimates to prove that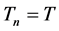 
is independent on
.
Lemma 1.
The solutions 
of the approximate system 1.9 are defined uniquely by 1.7.
Additionally, the following estimates are valid. For all 
there exists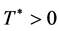 
such that 1)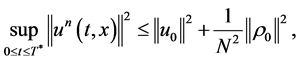 
2) 
for all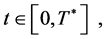 
3) 
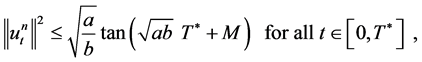
4) 
for all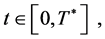 
5) 
for all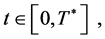 
6) 
for all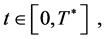 
where the positive constants a, b, M and 
depend only on the initial data 1.3, the parameter of the system N and the domain
.
Remark.
The values of the constants a, b, M and 
are given below in 1.22, 1.28 and 1.29.
Proof.
For 
we introduce the following auxiliary real-valued function
.
We observe that
. (1.13)
After multiplying each equation of 1.9 by 
and summing them with respect to
, we obtain
.
In this way, choosing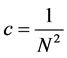
, we have that
. (1.14)
Therefore, 
for all t, and thus
. (1.15)
In particular, we have
. Thus the statement “a)” of the Lemma is proved.
From 1.14 we obtain that
(1.16)
which will prove the statement “b)”. Indeed,
Now, differentiating 1.9, we obtain
.
We multiply the last relations by 
and sum them with respect to k:
.
Therefore, keeping in mind that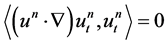
, we have
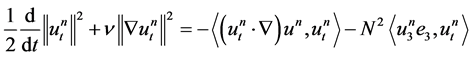. (1.17)
We would like to estimate the right-hand terms in 1.17. Evidently, from 1.15 we obtain
(1.18)
We will need the following estimate:
(1.19)
On the other hand, from the generalized Hölder inequality and the interpolation inequality
, we can estimate the term
(1.20)
From the Young inequality with “ε” for
, 
, 
,
we obtain
(1.21)
Now, using 1.19 and the inclusion Sobolev inequality
, we have
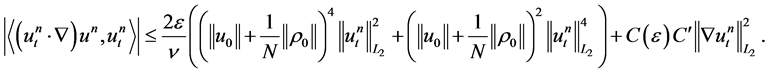
If we choose 
such that
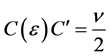, then the last estimate, together with 1.17 and 1.18, implies
(1.22)
Evidently, from 1.22 we have
, (1.23)
from which, after integrating with respect to t, it follows that
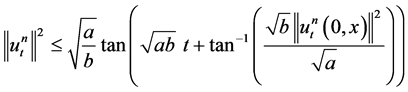. (1.24)
Now, to obtain a uniform upper estimate with respect to n for
, we only need to prove such estimate for
. We remind that the system
, being formed by eigenfunctions of Stokes operator is orthonor mal in
, and also in 
with the scalar product
, as well as in 
with the scalar product
, where P is an orthogonal projection of 
onto
. From 1.9 we have
.
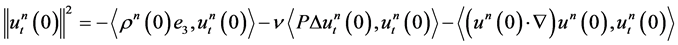Proceeding analogously to 1.17-1.21 and also using Lemma 1 from [11], we obtain
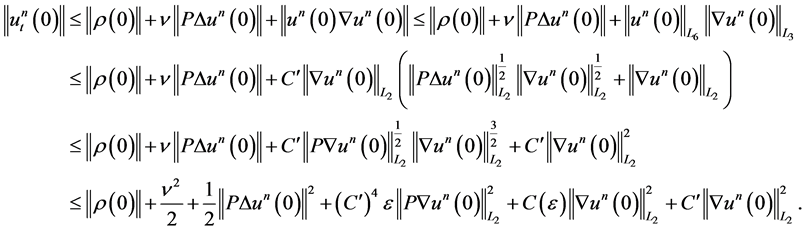
If we choose
, then we finally have
(1.25)
Now, from the Bessel inequality and the properties
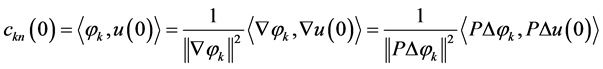, (1.26)
we can express 1.25 as
(1.27)
In this way, using 1.27 and the evident inequality
, we can estimate 1.24 as
(1.28)
where
.
Taking
, we assure that 
and thus we obtain the result that for all
there exists 
such that
, (1.29)
which proves the statement “c)” of the Lemma. It is easy to see that the statement “d)” is a direct consequence of 1.19 and 1.29. The statement “e)” of the Lemma is obtained immediately if we integrate both sides of 1.29 with respect to t. It remains to prove the statement “f)”. For that, we use 1.15 and 1.16 and therefore obtain
which concludes the proof of the Lemma.
We would like to obtain now more estimates for the approximate solutions 
with an intention to show that their limit, which is an obvious candidate for a solution of 1.2 - 1.4, would preserve certain regularity properties of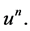 
Lemma 2.
For all 
and for all 
there exists a constant 
which does not depend on
, such that the following estimate is valid:
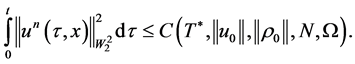
Proof.
We continue using the notation of P as an orthogonal projection of 
onto
. Let 
be eigenvalues corresponding to the eigenfunctions 
of the Stokes operator. We multiply 1.9 by 
and sum up the resulting equations with respect to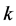
. In this way, we have
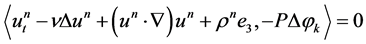. (1.31)
We would like to estimate the following term in 1.31:
. (1.32)
By using Cauchy and Hölder inequality, together with the inequality
, we obtain
. (1.33)
Now we use Sobolev inclusion inequality and Lemma 1 from [11], which allows us to estimate 1.33 as
(1.34)
We take
, consider the inequality 
and use the property
.
Proceeding in this way, we obtain
Now, if we take
, we will finally have
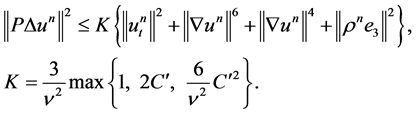(1.35)
The term 
on the right side of 1.35 can be estimated by 1.29. The terms
, can be estimated analogously, we use the statement “d)” of Lemma 1 and the inequality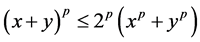
where we consider p = 2 and p = 3. Now, taking into account the properties
(1.36)
(1.37)
we can proceed estimating the integral of 1.35 as follows:
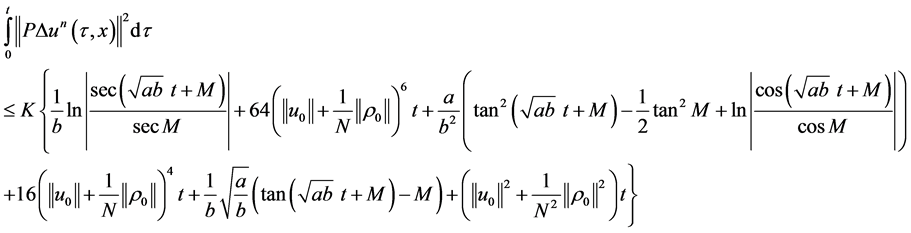
(1.38)
We note that the estimate 1.38 is valid for
. From 1.28 - 1.29 we have that the value 
is chosen in such a way that the right side of 1.38 is positive. Finally, we use the result from [15] where there is shown that in the functional space
, the norms 
and 
are equivalent, which concludes the proof.
Theorem 1.
Let 
be a bounded domain with the boundary of the class
, and let
,
.
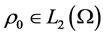Then, there exists an interval 
and there exist the functions 
which satisfy the system 1.2 and the conditions 1.3 - 1.4 in sense of 1.5 - 1.6, such that
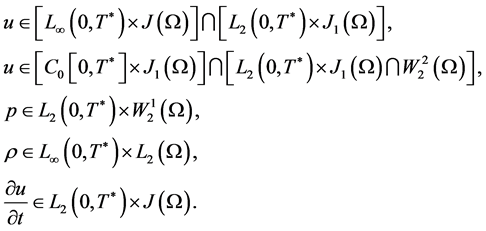
Proof.
From Lemma 1 and Lemma 2 we have that there exist a function u and a subsequence of 
(which, for brevity, we will denote also as
), such that
(1.39)
We note that the inclusion 
is compact and continuous, and that 
is bounded in
from Lemma 1. On the other hand, from the statement “c)” of Lemma 1 we have that for
and
, the following estimate holds:
(1.40)
In this way, from 1.39, 1.40 and Lemma 24.5 [12], it follows that 
belongs to a compact set in
. Therefore, the subsequence in 1.39 can be chosen in such a way that
(1.41)
It is easy to see that u satisfies the regularity properties of the Theorem. Indeed, since
and 
then, from Theorem IV.5.11 [15] we obtain that
. Using Sobolev inequality we have the estimate
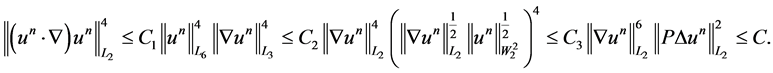
Therefore,
; which, in turn, implies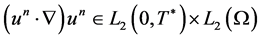
. Nowlet us show that u satisfies 1.5. Evidently, 
and 
satisfy 1.5 for
(1.42)
Since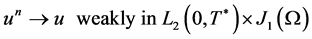
, then
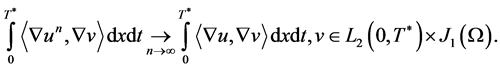
Analogously, we have that 
It remains to prove the limit
(1.43)
To verify 1.43, we note first that
(1.44)
We integrate by 
the relation 1.44 and use the properties that 
is uniformly bounded in
and that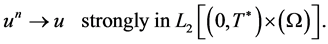 
In this way, we obtain that 1.43 is valid.
Now, we pass to the limit for 
in
and thus obtain
(1.45)
for the functions 
from 1.42. Due to the density of the set 1.42, we have that 1.45 is valid for all the functions 
from Definition 1, which completes the proof.
2. Uniqueness of the Solutions
Theorem 2.
The weak solution in sense of Definition 1, is unique.
Proof.
Let us exchange 
by 
and thus rewrite the system 1.2 in a more symmetrical way:
(2.1)
(2.2)
Let 
and 
be two solutions of 2.1 - 2.2 which satisfy the conditions 1.3 - 1.4 and also the conditions of Theorem 1. We denote
, and thus obtain
(2.3)
From 2.2 we have
. We observe that we can express 2.3 as follows:
(2.4)
We multiply 2.4 by U, integrate by parts in
. In this way, we have
(2.5)
By using the generalized Hölder inequality and Young inequality, together with the inequity
, we can estimate the last term in 2.5 as
(2.6)
If we take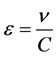
, then we will have the estimate
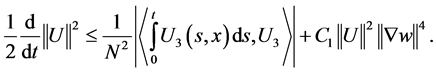(2.7)
Now we would like to estimate the term
. It is easy to see that
In this way, from 2.7 we obtain the estimate
(2.8)
Now, let us consider the following initial value problem for the function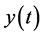
:
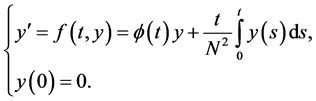(2.9)
Evidently, for continuous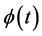 
the unique solution of the problem 2.9 is
.
By comparison principle, therefore, for every solution of the differential inequality
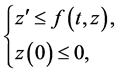
the property holds: 
In this way, we conclude from 2.9 that
, which implies that
.
Using 2.2 we obtain also that
, and thus the theorem is proved.
Acknowledgements
This research was partially supported by “Fondo de Investigaciones Facultad de Ciencias-Uniandes”.