Effects of Variable Viscosity on Hydromagnetic Boundary Layer along a Continuously Moving Vertical Plate in the Presence of Radiation and Chemical Reaction ()
1. Introduction
The problem of heat and mass transfer in the boundary layer induced by a moving surface in a quiescent fluid is important in many engineering applications. For examples, in the extrusion of polymer sheet from a dye, the cooling of an infinite metallic plate in a cooling path, glass blowing continuous casting and spinning of fibers. Sakiadis [1] studied the boundary layer flow over a continuous solid surface moving with constant velocity in an ambient fluid. The flow is quite different from the boundary layer flow over a semi-infinite flat plate due to the entrainment of the ambient fluid. Tsou et al. [2] presented a combined analytical and experimental study of the flow and temperature fields in the boundary layer on a continuous moving surface. Erickson et al. [3] extended Sakiadis problem to include blowing or suction at the moving surface. Crane [4] studied the boundary layer flow caused by a stretching sheet whose velocity varies linearly with the distance from a fixed point on the surface. The magnetohydrodynamics of an electrically conducting fluid is encountered in many problems in geophysics, astrophysics, engineering applications and other industrial areas. Engineers employ magnetohydrodynamics principles in the design of heat exchangers, pumps, in space vehicle propulsion, thermal protection, control and re-entry and in creating novel power generating systems. In many metallurgical processes involve the cooling of many continuous strips or filaments by drawing them through an electrically conducting fluid subject to a magnetic field, the rate of cooling can be controlled and final product of desired characteristics can be achieved. Another important application of hydromagnetics to metallurgy lies in the purification of molten metals from non-metallic inclusions by the application of a magnetic field. Kumar et al. [5] studied hydromagnetic flow and heat transfer on a continuously moving vertical plate. Sharma and Mathur [6] investigated steady laminar free convection flow of an electrically conducting fluid along a porous hot vertical infinite plate in the presence of heat source or sink. On the other hand, at high temperature the effects of radiation in space technology, solar power technology, space vehicle re-entry, nuclear engineering applications are very significant. Many processes in industrial areas occur at high temperature and the knowledge of radiation heat transfer in the system can perhaps lead to a desired product with a desired characteristic. Raptis and Massalas [7] studied the radiation effect on the unsteady magnetohydrodynamic flow of an electrically conducting viscous fluid past a plate. Chamkha [8] investigated thermal radiation and buoyancy effects on hydromagnetic flow over an accelerating permeable surface with heat source or sink. Raptis et al. [9] discussed the effect of thermal radiation on MHD asymmetric flow of an electrically conducting fluid past a semi-infinite plate. All the above studies were confined to a fluid with constant viscosity. However, it is known that this physical property may change significantly with temperature. Hossain and Munir [10] analyzed a two-dimensional mixed convection flow of a viscous incomepressible fluid of temperature dependent viscosity past a vertical plate. Fang [11] studied the influence of fluid property variation on the boundary layers of a stretching surface. Hossain et al. [12] discussed the effect of radiation on free convection flow of a fluid with variable viscosity from a porous vertical plate. Mahmoud [13] studied the effects of radiation and variable viscosity on hydromagnetic boundary layer flow along a continuously moving vertical plate with suction and heat flux.
Many transport processes exist in nature and in Industrial applications in which the simultaneous heat and mass transfer occurs as a result of combined buoyancy effects of diffusion of chemical species. Chemical reaction effects on heat and mass transfer laminar boundary layer flow have been discussed by various authors [14-18] in various situations.
In this paper, the effects of variable viscosity on hydromagnetic boundary layer flow along a continuously moving vertical plate with uniform suction and heat flux has been studied.
2. Mathematical Formulation
Consider a steady boundary layer convective flow through porous medium of an electrically conducting visco-elastic fluid on a continuous surface, issuing from a slot and moving vertically with a uniform velocity 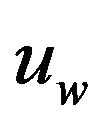 in a fluid and heat is supplied from the plate to the fluid at a uniform rate, in the presence of a uniform magnetic field of strength
in a fluid and heat is supplied from the plate to the fluid at a uniform rate, in the presence of a uniform magnetic field of strength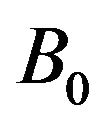 . Let the x-axis be taken along the direction of motion of the sheet and the y-axis be normal to the surface. The induced magnetic field is assumed to be negligible. It is assumed that there exists a first order chemical reaction between the fluid and the fluid species concentration. The physical model of the problem is shown in Figure 1.
. Let the x-axis be taken along the direction of motion of the sheet and the y-axis be normal to the surface. The induced magnetic field is assumed to be negligible. It is assumed that there exists a first order chemical reaction between the fluid and the fluid species concentration. The physical model of the problem is shown in Figure 1.
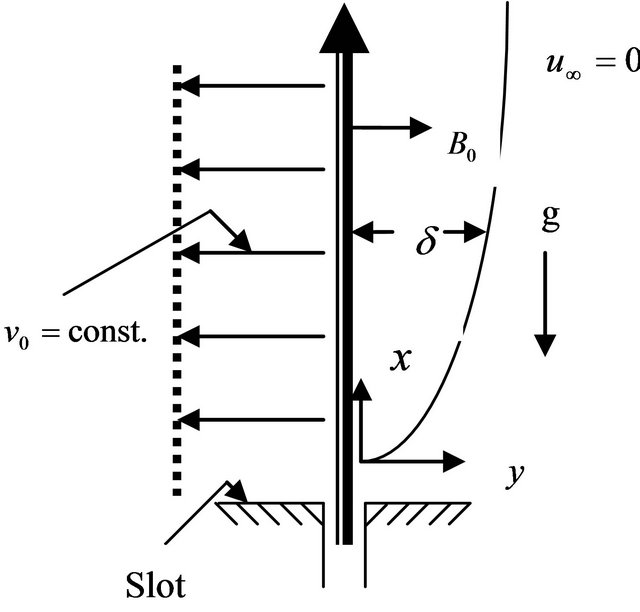
Figure 1. Physical model of the problem.
Under the above assumption, the equations for boundary layer flow are as follows:
 (1)
(1)
 (2)
(2)
Equation of heat transfer:
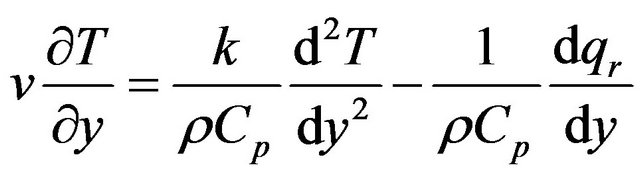 (3)
(3)
Equation of concentration:
 (4)
(4)
The corresponding boundary conditions are
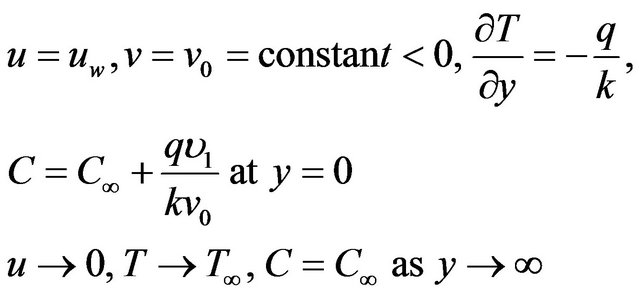 (5)
(5)
where 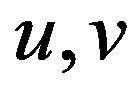 are the velocities along
are the velocities along 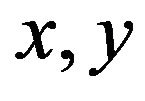 coordinates, respectively,
coordinates, respectively, 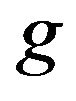 is the acceleration due to gravity,
is the acceleration due to gravity,  is the coefficient of thermal expansion,
is the coefficient of thermal expansion, 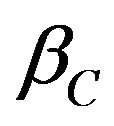 is the concentration coefficient,
is the concentration coefficient, 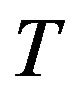 is the fluid temperature,
is the fluid temperature,  is the temperature of the fluid far away from the plate,
is the temperature of the fluid far away from the plate,  is the electrical conductivity,
is the electrical conductivity, 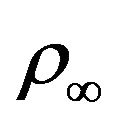 is the ambient density,
is the ambient density,  is the fluid viscosity,
is the fluid viscosity, 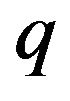 is the heat flux,
is the heat flux,  is the thermal conductivity,
is the thermal conductivity,  is the specific heat at constant pressure,
is the specific heat at constant pressure,  is the radiative heat transfer,
is the radiative heat transfer,  is the normal velocity at the plate,
is the normal velocity at the plate,  is the concentration,
is the concentration,  is the concentration in the fluid far away from the plate,
is the concentration in the fluid far away from the plate, 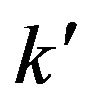 is the permeability of the porous medium.
is the permeability of the porous medium.
From the Equation (1), we get
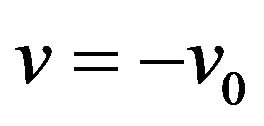 (6)
(6)
By using Rosseland approximation,  takes the form [3]
takes the form [3]
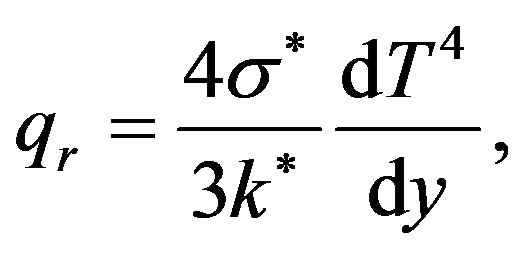 (7)
(7)
where 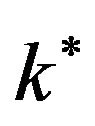 is the mean absorption coefficient and
is the mean absorption coefficient and  is the Stefan-Boltzmann constant.
is the Stefan-Boltzmann constant.
The temperature differences within the fluid assumed sufficiently small such that  may be expressed as a linear function of the temperature. Expanding
may be expressed as a linear function of the temperature. Expanding 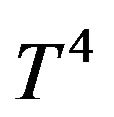 in Taylor series about
in Taylor series about 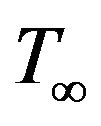 and neglecting the higher order terms, we get
and neglecting the higher order terms, we get
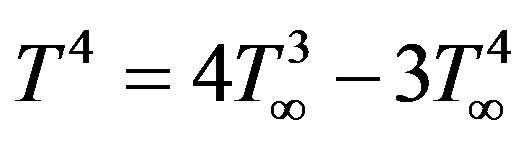 (8)
(8)
By using Equations (6)-(8) then Equation (3) gives
 (9)
(9)
Introducing the following non-dimensional quantities:
 (10)
(10)
In view of Equation (10), Equations (2), (9), and (4) reduce to the following non-dimensional form:
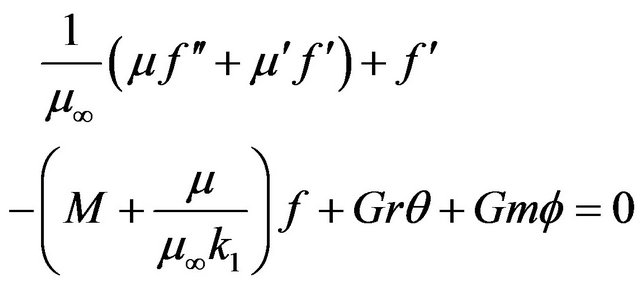 (11)
(11)
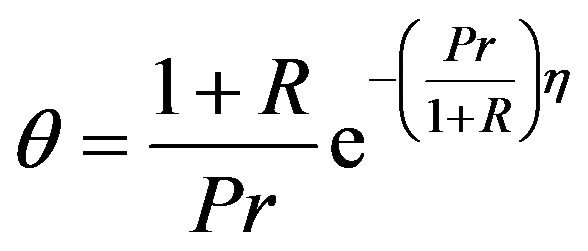 (12)
(12)
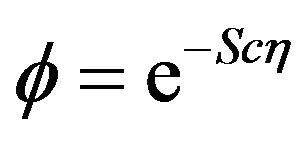 (13)
(13)
The corresponding boundary conditions are
 (14)
(14)
where the prime denote differentiation with respect to 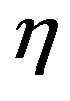 and
and 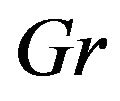 is the thermal Grashof number,
is the thermal Grashof number, 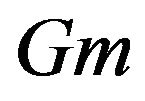 is the solutal Grashof number,
is the solutal Grashof number, 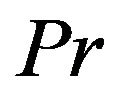 is the Prandtl number,
is the Prandtl number,  is the Hartmann number,
is the Hartmann number, 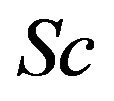 is the Schmidt number,
is the Schmidt number, 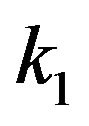 is the porous parameter,
is the porous parameter, 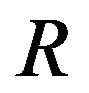 the radiation parameter.
the radiation parameter.
The fluid viscosity  was assumed to obey the Reynolds model [13],
was assumed to obey the Reynolds model [13],
 (15)
(15)
where 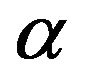 is a parameter depending on the nature of the fluid.
is a parameter depending on the nature of the fluid.
Using, Equation (13) in the Equation (11) we obtain,
 (16)
(16)
3. Method of Solution
1) Case of constant viscosity:
For , from Equation (16), we have
, from Equation (16), we have
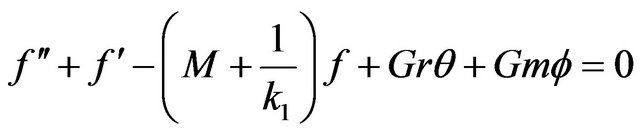 (17)
(17)
Solving (17) under boundary condition (14), we get
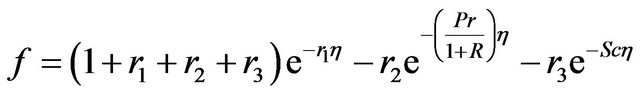 (18)
(18)
where
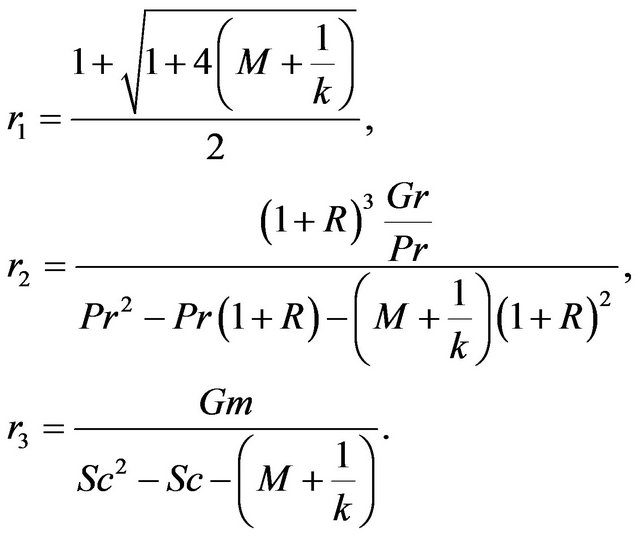
2) Variable viscosity case:
On taking into account the solution for temperature and concentration, we solved numerically the Equation (16) under the boundary conditions (14) using the RungeKutta fourth order technique with guessing  by shooting technique.
by shooting technique.
The skin friction coefficient is defined as
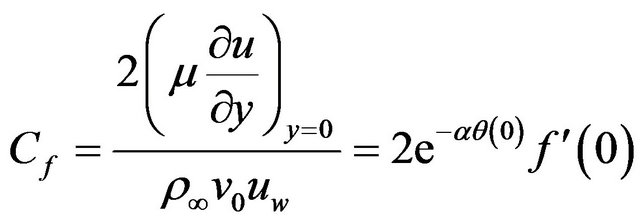 (19)
(19)
4. Results and Discussion
In order to see the physical impact of the variable viscosity 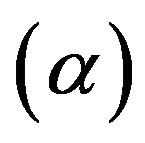 on the velocity field, the graphical representation of results is important. For the purpose of discussing the effect of variable viscosity on the flow profiles within the boundary layer, numerical calculations have been carried out for various values involved in the problem with fixed values of
on the velocity field, the graphical representation of results is important. For the purpose of discussing the effect of variable viscosity on the flow profiles within the boundary layer, numerical calculations have been carried out for various values involved in the problem with fixed values of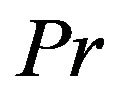 . The value of
. The value of 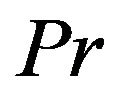 is taken to be
is taken to be 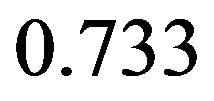 for air. The effect of
for air. The effect of  on dimensionless velocity
on dimensionless velocity 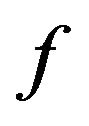 are illustrated in Figures 2-4 with
are illustrated in Figures 2-4 with 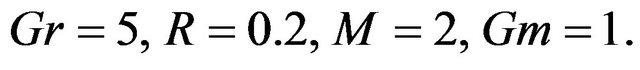
It is observed from the Figure 2 that velocity  increases as the viscosity
increases as the viscosity  of air decreases. The velocity distribution attains a distinctive maximum value in the vicinity of the plate and then decreases to approach a free stream value.
of air decreases. The velocity distribution attains a distinctive maximum value in the vicinity of the plate and then decreases to approach a free stream value.
Figure 3 shows the effects of Schmidt number on the velocity profile. As the Schmidt number increases there is reduction in the fluid velocity. The fluid velocity increased and reached its maximum value at very short distance from the plate and then decreases to approach a free stream value.
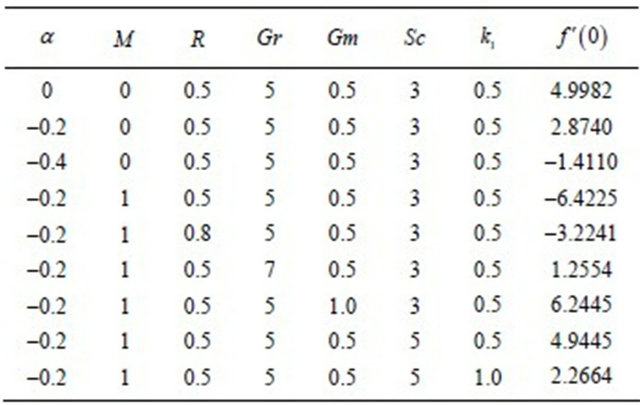
The effect of the porous parameter on velocity profile is shown in Figure 4. From the figure it is observed that fluid velocity increases with the increase in the porous parameter. Table 1 present the variation of the skin friction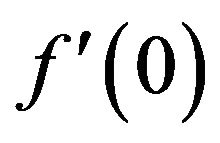 for various values of
for various values of 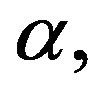 Hartmann number
Hartmann number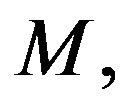 radiation parameter
radiation parameter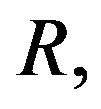 thermal Grashof number
thermal Grashof number solutal Grashof number
solutal Grashof number 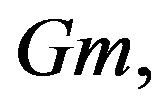 Schmidt number
Schmidt number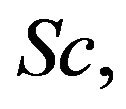 porous parameter
porous parameter with
with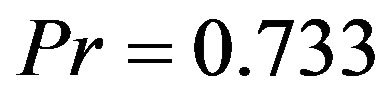 .
.
It is seen from the Table 1 that the skin-friction coefficient increases as the viscosity parameter, the radiation parameter, thermal Grashof number or solutal Grashof number increases. But the increasing of the magnetic parameter, Schmidt number or porous parameter leads to a decrease in the skin-friction.
5. Conclusion
The governing equations for boundary layer flow and mass transfer of a steady viscous, incompressible elec-
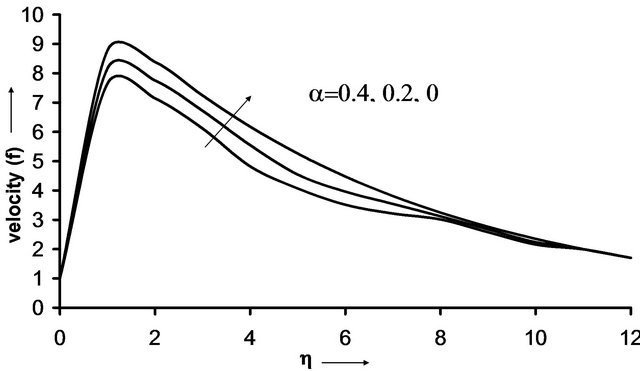
Figure 2. Velocity distribution for various values of 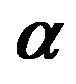 with
with 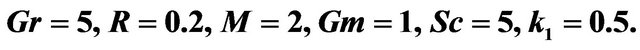
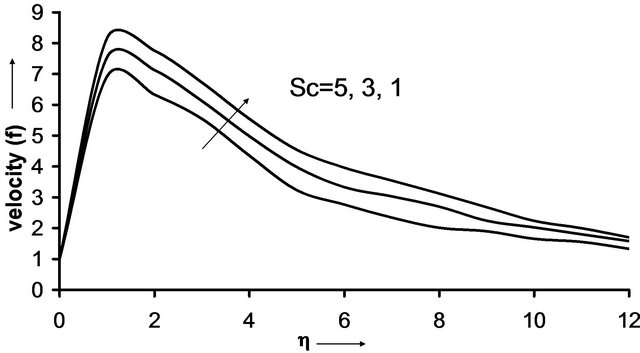
Figure 3. Velocity distribution for various values of 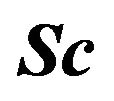 with
with 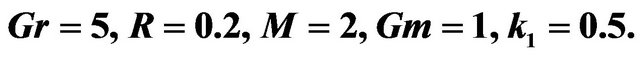

Figure 4. Velocity distribution for various values of  with
with 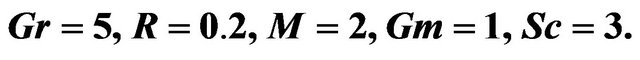
Table 1. Numerical values of 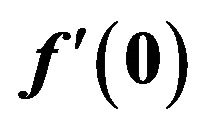 for different
for different .
.
trically conducting fluid with variable viscosity over a continuously moving vertical porous plate in the presence of magnetic field and radiation has been investigated. It was found that when viscosity parameter and porous parameters were increased, the fluid velocity increased. However, velocity decreases as the Schmidt number decrease. In addition, it was found that the skin-friction coefficient increased due to increase in the viscosity parameter, the radiation parameter, thermal Grashof number or solutal Grashof number. But the increasing of the magnetic parameter, Schmidt number or porous parameter leads to a decrease in the skin-friction.