Finite Element Analysis with Paraxial & Viscous Boundary Conditions for Elastic Wave Propagation ()
1. Introduction
In many dynamic problems, the analysts are confronted with the problem of wave propagation in infinite or semiinfinite media. The complex geometry or/and non-homogeneity disturb or prohibit to find the closed-form solutions to those problems. In this reason various numerical techniques are needed. But since such discrete models used are necessarily finite in size, echoes would develop at the artificial boundaries if no appropriate action was taken. Absorbing boundaries are mathematical artifacts used to prevent wave reflections at the boundaries of discrete models for infinite media under dynamic loads. A number of these boundaries have been proposed in the past three decades and used with various degrees of success. The collection of absorbing boundaries can be grouped into two broad classes: nonlocal and local absorbing boundaries. Nonlocal boundaries are exact, robust, accurate, and stable, but some of those are properly defined only in the frequency domain, and cannot be used for problems involving material nonlinear effects. And for some of those the exact condition is not available or is too complicated to be practical. For these reasons, a number of local absorbing boundaries have been proposed. Local absorbing boundaries may be good energy absorbers, but they are not perfect ones, therefore, a residual echo may be present in the solution. However, the accuracy of some classes of the local absorbing boundaries can be increased by taking higher order approximations for boundary conditions. But the various sequence of such boundary conditions make the absorbing boundary conditions have complex mathematical forms with partial derivatives, and thus this complicates the application of such local absorbing boundary conditions to finite element analysis. Paraxial boundary conditions are such kinds of local boundary conditions, which are based on paraxial approximations of the one-way wave equations, and thus the application of those to finite element analysis is difficult. In this study, to do this, a penalty functional is newly proposed and the existence and uniqueness of the extremum of the proposed functional is demonstrated. The penalty functional proposed in this study enables to derive the functional including not only the total potential energy but also paraxial boundary conditions in elastic media and thus to analyze the elasticity problems with the paraxial boundary conditions. Consequently, it may be expected that the proposed approach can be applied to any local boundary conditions based on approximations of the one-way wave equations. Viscous boundary conditions which are also some kinds of local boundary conditions are most convenient to apply to finite element analysis, but it is known that the capacity is not good. In this study the study on improving the capacity of viscous boundary conditions is implemented. Using the concept of energy ratio between the reflected waves and the incident wave, the efficiency of customary viscous boundary conditions can be improved for an arbitrary angle of incidence and materials. Finally, for the numerical analysis of elasticity with paraxial boundary conditions and the modified viscous boundary conditions, the coding of the finite element models is implemented, and the efficiency of those boundary conditions is investigated.
2. Paraxial and Viscous Boundary Conditions
2.1. Paraxial Boundary Conditions
Paraxial boundary conditions are based on the paraxial approximations of the one-way wave equations, which were developed for scalar wave equation [1-3] and for the elastic wave [4]. The absorbing boundary conditions should be chosen such that its dispersion relation is a good approximation of the interior dispersion relation for outgoing waves, and the boundary conditions together with the differential equation should form a well posed problem. The better the boundary conditions describe outgoing waves the smaller will be the reflection [5].
Figure 1 schematically shows the dispersion relation for a plane wave and Equation (1) is its mathematical form, where
, 
are xand y-directional spatial wave lengths, and 
and 
are xand y-directional wave numbers respectively.
Using Equation (1), the first and the second down-going paraxial boundary conditions, Equations (2) and (3) can be derived [6].
(1)
(2)
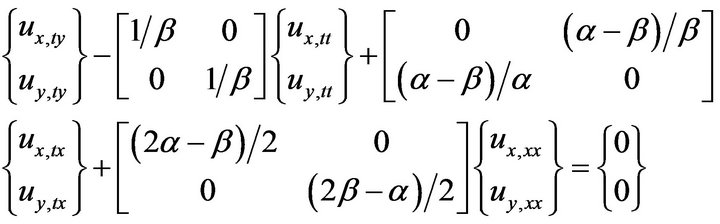(3)
Figure 1. Dispersion relation for a plane wave.
2.2. Viscous Boundary Conditions
Figure 2 shows the basic idea of a viscous boundary for plane strain. The energy arriving at the boundary in Figure 2 will be absorbed if tractions, Equations (4)-(5) are applied to the boundary which are equal in magnitude and opposite in direction to the stresses caused by the incident wave.