Journal of Modern Physics
Vol.3 No.8(2012), Article ID:21666,7 pages DOI:10.4236/jmp.2012.38088
Surface Morphology Dynamics in ITO Thin Films
Department of Physics, University of Bu Ali Sina, Hamedan, Iran
Email: d_raoufi@yahoo.com
Received October 13, 2011; revised November 13, 2011; accepted January 10, 2012
Keywords: ITO; Thin Film; Fractal Analysis; Morphology
ABSTRACT
In this study, indium tin oxide (ITO) thin films were prepared by electron beam evaporation method on float glass substrates at room temperature (RT). The surface morphology and dynamic scaling behavior of the films were studied by atomic force microscopy (AFM). It was found that average surface roughness values decreased as the film thickness increased from 100 nm to 350 nm. Fractal geometry and statistical physics techniques have been used to study a variety of irregular films within a common framework of the variance thickness. The Hurst exponent H and growth exponent b for ITO thin films were determined to be 0.73 ± 0.01 and 0.078, respectively. Based on these results, we suggest that the growth of ITO thin films can be described by the combination of the Edwards-Wilkinson equation and Mullins diffusion equation.
1. Introduction
Indium tin oxide (ITO) is an n-type wide band-gap (3.3 - 4.3 eV) semiconductor which by doping with tin, the density of the carrier can be increased up to the Mott critical ((1020/cm3), and the highly degenerated semiconductor is formed. This semiconductor shows high transmission in the visible and near-IR regions of the spectrum [1,2]. It is widely used as a transparent electrode in various optoelectronic devices such as solar cells, liquid crystal displays (LCDs), organic light-emitting diodes (OLEDs) and other flat panel displays (FPDs) [3,4]. Numerous deposition techniques have been utilized to prepare ITO thin films such as DC/RF magnetron sputtering [5], ion beam sputtering [6], electron beam evaporation [7], pulsed laser deposition [8], spray pyrolysis [9] and chemical vapor deposition [10]. The surface roughness characterization is an important problem for both applied and basic science. Both real space imaging techniques such as, atomic force microscopy, scanning tunneling microscopy, transmission electron microscopy, secondary electron microscopy and optical imaging techniques, and diffraction techniques such as, electron, atom, light and X-ray scattering have been extensively used to investigate the rough surfaces [11]. Therefore, the surface roughness of all those layers which are the basis for subsequent deposition processes were systematically studied by atomic force microscopy (AFM). It has been a challenge to quantitatively describe the morphology of rough surfaces and interfaces of thin films [12]. This is largely because of the complexity and the large variation in the surface topography. It has been realized recently that the fractal geometry and scaling concepts proposed by Mandelbrot [13] can concisely describe the rough surface morphology. The surface morphology at different scales is believed to be self-similar and related in the fractal geometry. The surface morphology at each scale can be described by a similar set of geometry parameters. Fractal descriptions characterize the deviation of the surface from Euclidian geometry by relating parameters, such as using a non-integer exponent called the fractal dimension [14]. The concept of fractal dimensionality, in contrast of traditional techniques, has proven very successful both in applying to a wide variety of complex surface geometries and in advancing our understanding of how the geometry affects the physical properties of the system [15]. One of the directions of using fractal characteristic in technical diagnostics is tied to the fact that the time series of the main well performance indicators measurements quite often have fractal structure [16]. Some records of observable quantities are in the form of ordered sequences (e.g., time series) and their fractal properties are commonly studied by means of a scaling analysis of the underlying fluctuations [17]. Rescaled range analysis (R/S) is an important part of fractal theory [18] and a strong theoretical back up, its statistical limitations for scaling (Hurst) exponent estimation are well established [19]. Quantitative information is expressed by Hurst’s exponent H. the Hurst rescaled range (R/S) analysis were applied to determine the fractal dimension and Hurst exponent of ITO thin films. The Hurst rescaled range (R/S) analysis directly relates the Hurst exponent H to the fractal dimension D and can bypass noise included in the AFM images. In this study, we employ atomic force microscopy to investigate surface roughness parameters of ITO films prepared by electron beam evaporation technique. AFM images of the evaporated deposition ITO films indicate changes in surface behavior of the film at different thickness.
2. Experimental
ITO thin films, with different thicknesses (100 to 350 nm), were prepared by electron beam evaporation method on polished float (soda-lime) glass substrates at room temperature. The target material used in this study was an ITO pellet (Merck Co.) with nominal 99.9% purity In2O3:SnO2 (90 wt% and 10 wt%, respectively). Before loading the glass substrates into the chamber, they were ultrasonically cleaned in acetone, ethanol and deionizer (DI) water for 10 min. Finally, they were dried with nitrogen gas. The optimum conditions of films depositing were achieved in the presence of oxygen with an initial vacuum (base pressure) of 1 × 10–6 mbar, an accelerating voltage of 1 - 10 kV, electron beam current 10 - 12 mA. For control the deposition rate, the oxygen (99.99%) is introduced into the deposition system from a steel tube through a calibrated leak valve. By using the data from a quartz crystal thickness measurement system, the electron gun current is automatically adjusted to have a constant deposition rate. The deposition rate was 0.1 nms–1 and the thickness of the ITO thin films varied in the range of 100 - 350 nm. After prepare films, each sample was taken out for immediately ex situ measurements to study the surface morphology of the films. The surface morphology of the thin films was characterized with an Atomic Force Microscope (AFM-Park Scientific Instruments) under ambient conditions. The scan sizes were 0.25 × 0.25 μm2 and 1 × 1 μm2. All the surface images were obtained in the contact mode using silicon nitride tips with approximate tip radius of 10 nm, and the height of the surface relief was recorded at a resolution of 256 pixels × 256 pixels. A variety of scans were acquired at random locations on the film surface. To analyses the AFM images, the topographic image data were converted into ASCII data.
3. Results and Discussions
3.1. Structural Properties
First, in order to study the microstructure of the ITO thin films, prepared at room temperature, the X-ray diffractometer (XRD) measurements were performed.
Figure 1 shows a typical XRD pattern of the ITO films. It is noted that no diffraction peak except a broad background (2θ = 15˚ - 35˚) is observed for the thin film. This feature indicates an amorphous and/or a nanocrystalline structure for the prepared ITO film [3].
3.2. Evolution Features of ITO Thin Films
Figures 2(a)-(d) show the AFM images of ITO thin films deposited on a glass substrate on the over scan area of 1 × 1 μm2. The one-dimensional cross section scans of surface profiles are also plotted in Figures 3(a)-(d) of the ITO thin films with various thicknesses of 100 nm, 170 nm, 250 nm and 350 nm, respectively. Two typical morphological features are recognized readily by visual inspection of Figures 2 and 3. The first feature is that, the ITO thin films surfaces show continuous island-like structures, and with increasing the film thickness, these islands become smaller in both lateral and vertical directions. This evolution feature can be more easily observed, from the corresponding surface profiles of these films, in Figure 3. The second feature is that, the interface width w (or, root mean square roughness, RMS) as a function of film thickness where valleys, mountains and island clusters become smaller decreased as film thickness increased.

Figure 1. A typical XRD pattern of the ITO films prepared at room temperature.
 (a)
(a) (b)
(b) (c)
(c) (d)
(d)
Figure 2. An AFM image series of ITO thin films: (a) 100 nm; (b) 170 nm; (c) 250 nm; (d) 350 nm.
 (a)
(a) (b)
(b)
Figure 3. One-dimensional AFM surface profile scans of ITO thin films for: (a) 100 nm; (b) 170 nm; (c) 250 nm; (d) 350 nm.
The roughness calculation is the simple and the most used parameter for observation of changes in surface topography. In quantitative analyses on AFM images, it is known that the height roughness Ra and RMS have been used to describe the surface morphology. Ra is defined as the mean value of the surface height relative to the center plane, and RMS is the standard deviation of the surface height within the given area [20,21].
Denoting by h(i, j), the height of the surface measured by AFM at the point (i, j), N ´ N the total number of points at which the surface heights have been measured then the interface width w value of the surface is defined as [20]:
 (1)
(1)
where  represents the heights mean value of surface and defined as below.
represents the heights mean value of surface and defined as below.
 (2)
(2)
Interface width is very attractive because compute simplicity and has ability to summarize the surface roughness by a single value. The average roughness is another simple statistical measure and it is defined as:
 (3)
(3)
The interesting results (RMS and Ra) have been plotted in Figure 4" target="_self"> Figure 4. From this figure, it is noted that the average roughness Ra and w values decreased with increasing the film thickness. This behavior is due to the reflecting nucleation, coalescence and continuous film growth processes, i.e. Volmer-Weber type initial growth [22]. The above analyses indicate that average roughness Ra and w are strongly affected by the degree of aggregation and cluster size of the thin films. The different cluster size influences the surface roughness of the films [23].
However, these parameters are rather inadequate to provide a complete description of the irregularity of thin film surfaces [24,25]. These simple statistical measurements give only height information, and therefore cannot fully characterize the surface.
3.3. Scaling Behavior of ITO Thin Films
Figure 5 shows the rescaled range (R/S) of ITO thin films. The Hurst rescaled range analysis is a technique proposed by Henry Hurst in 1951 [26] to test presence of correlations in empirical time series. The main idea behind the R/S analysis is that one looks at the scaling behavior of the rescaled cumulative deviations from the mean, or the distance the system travels as a function of time. Consider a time series in prices of length P. This time series is then transformed into a time series of logarithmic returns of length N = P − 1 such that

Figure 4. w (RMS) and Ra for ITO thin films.
 (4)
(4)
Time period is divided into m contiguous sub-periods of length n, such that . Each sub-period is labeled by Ia, with
. Each sub-period is labeled by Ia, with . Then, each element in Ia is labeled by Nk, such that
. Then, each element in Ia is labeled by Nk, such that . For each subperiod Ia of length n the average is calculated as:
. For each subperiod Ia of length n the average is calculated as:
 (5)
(5)
Thus, Ma is the mean value of the  contained in the sub-period Ia of length n. Then, we calculate the time series of accumulated departures from the mean (Xk,a) for each sub-period Ia, defined as:
contained in the sub-period Ia of length n. Then, we calculate the time series of accumulated departures from the mean (Xk,a) for each sub-period Ia, defined as:
 (6)
(6)
As can be seen from Equation (6), the series of accumulated departures from the mean always will end up with zero. Now, the range that the time series covers relative to the mean within each sub-period is defined as:
 (7)
(7)
The next step is to calculate the standard deviation for each sub-period Ia,
 (8)
(8)
Then, the range for each sub-period ( ) is rescaled by the corresponding standard deviation (
) is rescaled by the corresponding standard deviation ( ). Recall that we had m contiguous sub-periods of length n. Thus, the average R/S value for length or box n is
). Recall that we had m contiguous sub-periods of length n. Thus, the average R/S value for length or box n is
 (9)
(9)
Now, the calculations from Equations (4)-(9) must be repeated for different time horizons. This is achieved by successively increasing n and repeating the calculations until we have covered all integer ns. One can say that R/S analysis is a special form of box-counting for time series. However, the method was developed long before the concepts of fractals. After having calculated R/S values for a large range of different time horizons n, we plot  versus
versus  By performing a leastsquares regression with
By performing a leastsquares regression with  as the dependent variable and
as the dependent variable and 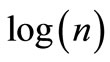 as the independent one, we find the slope of the regression which is the estimate of the Hurst exponent H [27], that is
as the independent one, we find the slope of the regression which is the estimate of the Hurst exponent H [27], that is
 (10)
(10)
The Hurst exponent (H) and the fractal dimension Df are related as [28]:
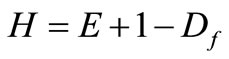 (11)
(11)
where E + 1 is the dimension of the embedded space (E = 1 for a profile; E = 2 for a plan) [3]. The Hurst exponent, who varies between 0 and 1, describes the fractal characteristics of time series. In theory, H = 0.5 means that the time series is independent, but as mentioned above the process need not be Gaussian e.g. the system obeys a random walk [29,30]. If  characterizes the persistence of the time series (called the memory effect). It is also a main characteristic of non-linear dynamical systems that there is a sensitivity to initial conditions which implies that such a system in theory would have an infinite memory. The persistence implies that if the series has been up or down in the last period then the chances are that it will continue to be up or down, respectively, in the next period. This behavior is also independent of the time scale we are looking at. When
characterizes the persistence of the time series (called the memory effect). It is also a main characteristic of non-linear dynamical systems that there is a sensitivity to initial conditions which implies that such a system in theory would have an infinite memory. The persistence implies that if the series has been up or down in the last period then the chances are that it will continue to be up or down, respectively, in the next period. This behavior is also independent of the time scale we are looking at. When , we have anti-persistence. This means that whenever the time series have been up in the last periodit is more likely that it will be down in the next period. Thus, an anti-persistent time series will be choppier than a pure random walk with H = 0.5 [31].
, we have anti-persistence. This means that whenever the time series have been up in the last periodit is more likely that it will be down in the next period. Thus, an anti-persistent time series will be choppier than a pure random walk with H = 0.5 [31].
Figure 5 presents the rescaled range analysis of ITO thin films were prepared on glass slide substrates at room temperature by electron beam evaporation technique. From this graph, the H value was obtained by means of a statistical regression as the slope of the straight line. The average slope of the curves represent the Hurst exponent H = 0.73 ± 0.01, which characterizes the time series structure. The process is a persistent process, i.e., long memory. The experimental results show that Hurst coefficient did not more change with increase thickness, i.e., the Hurst exponent for all samples are very close, this suggests that the dynamics of roughness formation may be quite similar during the increase thickness of the ITO thin films.
The self-affine structure of the films is further confirmed by measurements of another important parameter β (growth exponent), which characterizes the time evolution of a self-affine surface in the following way: provided that the deposition time t is lower than a saturation value tx, the interface width w is proportional to tβ: as in
 (12)
(12)
Since the deposition time t and the film thickness d are proportional by the (constant) deposition rate r (d = rt), to evaluate β we can report w as function of d using samples grown at different deposition times [32]. Figure 6 describes the dependence of the interface width w on thickness d for different ITO thin films. The thin solid line is the best liner fit indicating the growth exponent β, and the result of the fitting gives β = 0.078. We compare the scaling exponents (H and β) determined for ITO thin films with exponents suggested by theoretical models. In fact, ITO growth behavior is between noise-driven Mullins diffusion model and noise-induced Edwards-Wilkinson model.

Figure 6. log-log plot of w versus thickness of ITO thin films. Thin solid line indicates the growth exponent β.
Combining the smoothing mechanism with random fluctuations, one can describe the growth process by a Langevin equation in the form:
 (13)
(13)
where,  is the result of the Gibbs-Thompson relation describing the thermal equilibrium interface between the vapour and solid. The term
is the result of the Gibbs-Thompson relation describing the thermal equilibrium interface between the vapour and solid. The term  is the small slope expansion of the surface curvature, and the prefactor v is proportional to the surface tension coefficient. The second term
is the small slope expansion of the surface curvature, and the prefactor v is proportional to the surface tension coefficient. The second term  is the result of surface diffusion due to the curvature induced chemical potential gradient. The prefactor
is the result of surface diffusion due to the curvature induced chemical potential gradient. The prefactor  is proportional to the surface diffusion coefficient. We can see that the general Langevin equation is a combination of the EW equation and Mullins diffusion equation. The scaling parameter cannot be applied to Equation (12) because there is crossover from EW and Mullins equation. Therefore the
is proportional to the surface diffusion coefficient. We can see that the general Langevin equation is a combination of the EW equation and Mullins diffusion equation. The scaling parameter cannot be applied to Equation (12) because there is crossover from EW and Mullins equation. Therefore the  value is between the EW model,
value is between the EW model,  and the Mullins diffusion model,
and the Mullins diffusion model,  [33]. From the above analysis, we obtain the Hurst exponent (roughness exponent) H = 0.73 ± 0.01 and,
[33]. From the above analysis, we obtain the Hurst exponent (roughness exponent) H = 0.73 ± 0.01 and, 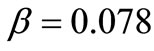 respectively. From the measured roughness exponent and growth exponent, we suggest that our ITO thin films growth behaviour is the combination of the Mullins diffusion model and the Edwards-Wilkinson model.
respectively. From the measured roughness exponent and growth exponent, we suggest that our ITO thin films growth behaviour is the combination of the Mullins diffusion model and the Edwards-Wilkinson model.
4. Conclusion
In this work, we have analyzed the changes of surface morphology and dynamic scaling behavior of ITO thin films prepared by electron beam deposition method on glass substrate for different film thicknesses. AFM images of the ITO thin films reveal the formation of a porous granular surface, while the surface roughness values are decreasing from 24.8 nm to 4.13 nm with increasing of the film thickness from 100 nm to 350 nm. In order of to quantify the dynamic scaling and irregularity of the ITO thin films in more detail, we employ the fractal concept. The Hurst exponent (roughness exponent) was determined by applying the rescaled range (R/S) analysis method. From the measured roughness exponent H and growth exponent β, the dynamic scaling was observed clearly after numerical correlation analysis. The growth process can be described by the combination of Mullins diffusion Model and Edwards-Wilkinson model.
5. Acknowledgements
The authors would like to thank Dr. G. R. Jafari, Department of Physics, Shahid Beheshti University, Tehran, for many useful discussions and for his help in the R/S analysis of the films.
REFERENCES
- H. Kim, A. Pique, J. S. Horwitz, H. Mattoussi, H. Murata, Z. H. Kafafi and D. B. Chrisey, “Indium Tin Oxide Thin Films for Organic Light-Emitting Devices,” Applied Physics Letters, Vol. 74, No. 23, 1999, pp. 3444-3446. doi:10.1063/1.124122
- I. Hamberg and C. G. Granqvist, “Evaporated Sn-Doped In2O3 Films: Basic Properties and Applications to Energy Efficient Windows,” Journal of Applied Physics, Vol. 60, No. 11, 1986, pp. R123-R159. doi:10.1063/1.337534
- D. Raoufi, A. Kiasatpour, H. R. Fallah and A. S. H. Rozatian, “Surface Characterization and Microstructure of ITO Thin Films at Different Annealing Temperatures,” Applied Surface Science, Vol. 253, No. 23, 2007, pp. 9085-9090. doi:10.1016/j.apsusc.2007.05.032
- D. Vaufrey, M. Ben Khalifa, J. Tardy, C. Ghica, M. G. Blanchin, C. Sandu and J. A. Roger, “ITO-on-Top Organic Light-Emitting Devices: A Correlated Study of OptoElectronic and Structural Characteristics,” Semiconductor Science and Technology, Vol. 18, No. 4, 2003, pp. 253- 260. doi:10.1088/0268-1242/18/4/310
- S. H. Shin, J. H. Shin, K. J. Park, T. Ishida, O. Tabata and H. H. Kim, “Low Resistivity Indium Tin Oxide Films Deposited by Unbalanced DC Magnetron Sputtering,” Thin Solid Films, Vol. 341, No. 1-2, 1999, pp. 225-229. doi:10.1016/S0040-6090(98)01531-4
- D. Kim, Y. Han, J. S. Cho and S. K. Koh, “Low Temperature Deposition of ITO Thin Films by Ion Beam Sputtering,” Thin Solid Films, Vol. 377-378, 2000, pp. 81-86. doi:10.1016/S0040-6090(00)01388-2
- D. C. Paine, T. Whitson, D. Janiac, R. Beresford and O. Y. Cleva, “A Study of Low Temperature. Crystallization of Amorphous Thin Film Indium-Tin-Oxide,” Journal of Applied Physics, Vol. 85, No. 12, 1999, pp. 8445-8450. doi:10.1063/1.370695
- T.-K. Yong, et al., “Pulsed Laser Deposition of Indium Tin Oxide Nanowires in Argon and Helium,” Materials Letters, Vol. 66, No. 1, 2012, pp. 280-281. doi:10.1016/j.matlet.2011.08.085
- E. Benamar, M. Rami, C. Messaoudi, D. Sayah and A. Ennaoui, “Structural, Optical and Electrical Properties of Indium Tin Oxide Thin Films Prepared by Spray Pyrolysis,” Solar Energy Materials and Solar Cells, Vol. 56, No. 2, 1999, pp. 125-139. doi:10.1016/S0927-0248(98)00151-2
- K. Maki, N. Komiya and A. Suzuki, “Fabrication of Thin Films of ITO by Aerosol CVD,” Thin Solid Films, Vol. 445, No. 2, 2003, pp. 224-228. doi:10.1016/j.tsf.2003.08.021
- A. Arnéodo, N. Decoster and S. G. Roux, “A WaveletBased Method for Multifractal Image Analysis: I. Methodology and Test Applications on Isotropic and Anisotropic Random Rough Surfaces,” The European Physical Journal B, Vol. 15, No. 3, 2000, pp. 567-600. doi:10.1007/s100510051161
- P. Meakin, “Fractal, Scaling and Growth Far from Equilibrium,” Cambridge University Press, London, 1998.
- B. B. Mandelbrot, “The Fractal Geometry of Nature,” Freemen Press, San Francisco, 1982.
- J. Russ, “Fractal Surfaces,” Plenum Press, New York and London, 1994.
- G. Binnig, C. F. Quate and C. Gerber, “Atomic Force Microscope,” Physical Review Letters, Vol. 56, No. 9, 1986, pp. 930-933. doi:10.1103/PhysRevLett.56.930
- A. A. Suleymanov, A. A. Abbasov and A. J. Ismaylov, “Fractal Analysis of Time Series in Oil and Gas Production,” Chaos, Solitons and Fractals, Vol. 41, No. 5, 2009, pp. 2474-2483. doi:10.1016/j.chaos.2008.09.039
- J. Alvarez-Ramirez, J. C. Echeverria and E. Rodriguez, “Performance of a High-Dimensional R/S Method for Hurst Exponent Estimation,” Physica A, Vol. 387, No. 26, 2008, pp. 6452-6462. doi:10.1016/j.physa.2008.08.014
- X.-A. Yin, X.-H Yang and Z.-F Yang, “Using the R/S Method to Determine the Periodicity of Time Series,” Chaos, Solitons and Fractals, Vol. 39, No. 2, 2009, pp. 731-745. doi:10.1016/j.chaos.2007.01.085
- A. W. Lo, “Long-Term Memory in Stock Market Prices,” Econometrica, Vol. 59, No. 5, 1991, pp. 1279-1313. doi:10.2307/2938368
- Reference Manual for Nanoscope III, Digital Instrument, Santa Barbara, 1996.
- J. D. Kiely and D. A. Bonnell, “Quantification of Topographic Structure by Scanning Probe Microscopy,” Journal of Vacuum Science & Technology B, Vol. 15, No. 4, 1997, pp. 1483-1493. doi:10.1116/1.589480
- Y. Shigesato, R. Koshi-ishi, T. Kawashima and J. Ohsako, “Early Stages of ITO Deposition on Glass or Polymer Substrates,” Vacuum, Vol. 59, No. 2-3, 2000, pp. 614-621. doi:10.1016/S0042-207X(00)00324-9
- R. Buzio, E. Gnecco, C. Boragno, U. Valbusa, P. Piseri, E. Barborini and P. Milani, “Self-Affine Properties of Cluster-Assembled Carbon Thin Films,” Surface Science, Vol. 444, No. 1-3, 2000, pp. L1-L6. doi:10.1016/S0039-6028(99)01066-3
- J. C. Arnault, A. Knoll, E. Smigiel and A. Cornet, “Roughness Fractal Approach of Oxidised Surfaces by AFM and Diffuse X-Ray Reflectometry Measurements,” Applied Surface Science, Vol. 171, No. 3-4, 2001, pp. 189-196. doi:10.1016/S0169-4332(00)00550-X
- J. M. Li, L. Lu, Y. Su and M. O. Lai, “Self-Affine Nature of Thin Film Surface,” Applied Surface Science, Vol. 161, No. 1-2, 2000, pp. 187-193. doi:10.1016/S0169-4332(00)00297-X
- H. E. Hurst, R. P. Black and Y. M. Simaika, “Long-Term Storage: An Experimental Study,” Constable, London, 1965.
- E. E. Peters, “Fractal Market Analysis,” Wiley, New York, 1991.
- N. Kannathal, U. Rajendra Acharya, C. M. Lim and P .K. Sadasivan, “Characterization of EEG-A Comparative Study,” Computer Methods and Programs in Biomedicine, Vol. 80, No. 1, 2005, pp. 17-23. doi:10.1016/j.cmpb.2005.06.005
- J. Feder, “Fractals,” Plenum Press, New York, 1988.
- M. Saitou, W. Oshikawa and A. Makabe, “Characterization of Electrodeposited Nickel Film Surfaces Using Atomic Force Microscopy,” Journal of Physics and Chemistry of Solids, Vol. 63, No. 9, 2002, pp. 1685-1689. doi:10.1016/S0022-3697(01)00254-2
- P. Norouzzadeh and G. R. Jafari, “Application of Multifractal Measures to Tehran Price Index,” Physica A, Vol. 356, No. 2-4, 2005, pp. 609-627. doi:10.1016/j.physa.2005.02.046
- R. Buzio, E. Gnecco, C. Boragno, U. Valbusa, P. Piseri, E. Barborini and P. Milani, “A Molecular-Beam Study of Methane Dissociative Adsorption on Oxygen-Precovered Pt{110}(1 × 2),” Surface Science, Vol. 444, No. 1-3, 2000, pp. 1-6. doi:10.1016/S0039-6028(99)01048-1
- Y. Zhao, G. Ching, T. Wang and M. Lu, “Characterization of Amorphous and Crystalline Rough Surface: Principle and Applications,” Academic Press, New York, 2001.


