Abstract

In this paper we present some identities for the sums of squares of Fibonacci and Lucas numbers with consecutive primes, using maximal prime gap G(x)~log²x, as indices.

Keywords

Maximal Gap, Lucas Numbers, Fibonacci Numbers, Sums of Squares

Share and Cite:

Received 18 September 2015; accepted 15 December 2015; published 18 December 2015

1. Introduction

The two most well-known linear homogeneous recurrence relations of order two with constant coefficients are those that define Fibonacci and Lucas numbers. 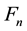denotes the 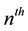Fibonacci number and 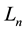denotes the Lucas number. The Lucas sequence is defined by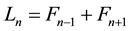. The Fibonacci numbers are generated by the recursion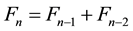. The Lucas numbers also have the property that for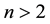,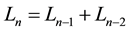. Note that a Lucas number is always greater than its corresponding Fibonacci numbers except for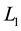. Fibonacci and Lucas numbers are represented by the same recurrence relation. This is the reason that Fibonacci and Lucas numbers have so many common or very similar properties.

Hundreds of Fibonacci and Lucas identities involving both Fibonacci and Lucas numbers appeared in various journals [1] -[3] and books [4] [5] over the years. Our goal in this paper is to present some identities concerning sums of squares of Fibonacci and Lucas numbers with consecutive primes as indices. Regarding consecutiveness of primes we consider maximal gap between consecutive primes.

, the maximal gap between consecutive primes is defined by many approximations [6] [7] . Among those we observed that 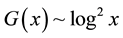gives the value nearest to the actual value while calculating sums of squares of consecutive primes. Based upon this, here we have chosen 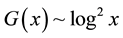and calculated sums of squares of Fibonacci and Lucas Primes.

2. Identities on Sums of Squares of Fibonacci and Lucas Numbers

Here the following formulae are repeatedly used.

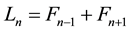
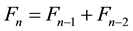
The difference between two consecutive primes () always being an even integer, the indices are taken as p and to calculate sums of squares of two Lucas numbers with indices as primes and its consecutive primes.

2.1. Proposition

where.

Proof.

Using the basic recurrence relation, for an odd prime p we have

Illustrations

As the number of primes is infinite we try to use, the maximal gap between consecutive primes as indicies. Through there are many formulae available for, in [8] . It is observed that while calculating sums of squares of consecutive primes gives the value nearest to the actual value. Hence has been used.

2.2. Proposition

Proof.

Again using the recurrence relation we have,

Now using Binet’s formula, sums of squares of two Fibonacci numbers with consecutive primes as indicies has been expressed in terms of Lucas numbers.

2.3. Proposition

Proof.

In general

Illustrations

As discussed in proposition 2.2, has been taken for this proposition also.

2.4. Proposition

Proof.

Finally, sums of squares of a Fibonacci and Lucas number is found.

2.5. Proposition

Proof.

Using Binet’s formula, we have

Notation

(The Floor of x)―The Greatest Integer ≤ x

Conflicts of Interest

The authors declare no conflicts of interest.

References