Abdelfattah Haily, Driss Harzalla
Department of Mathematics, Faculty of Sciences, University Chouaib Doukkali, El Jadida, Morocco.
DOI: 10.4236/iim.2015.72008   PDF    HTML   XML   10,391 Downloads   11,239 Views   Citations

Abstract

In this work, we study binary linear distinct weight codes (DW-code). We give a complete classification of -DW-codes and enumerate their equivalence classes in terms of the number of solutions of specific Diophantine Equations. We use the Q-extension program to provide examples.

Keywords

Distinct (Constante) Weigth Code, Automorphism Group, Extension Theorem of MacWilliams, Diophantine Equations

Share and Cite:

1. Preliminaries

One of the main objective of algebraic coding theory is to classify codes up to equivalence by using a list of invariants. The present work is following this way. We study here a class of linear binary codes whose all codewords have distinct weight and will give a classification theorems. Throughout this work all codes are

linear binary codes. We call an 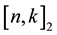-binary code every 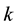dimensional subspace 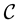of. Recall also that

the Hamming weight 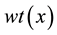of vector 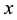is defined to be the number of nonzero components of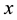. The mi- nimum of weights where is the minimal distance 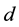of the code.

A Hamming isometry of 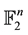is a linear application 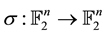such that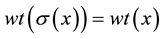, for every

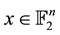. It is well known that in binary case, the isometries are merely the permutations of the coordinates, that is the elements of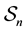, the permutation group of.

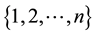Two codes and are said to be equivalent if there exists an isometry of such that. An automorphism of is a Hamming isometry such that. The automorphisms of form a subgroup of called the automorphism group of and we denote it by. Note also that the vector

space can be endowed with a product, so that becomes

a Boolean ring. Furthermore, , for every. The code is said

a constant-weight code (CW-code) if all nonzero codewords have the same weight. The dual of binary

Hamming codes are simplex codes of parameters. simplex codes are constant

weight code (CW-code).

Any permutation of the columns of a k by n binary matrix which maps the rows of into rows of the same matrix, is called an automorphism of the binary matrix [1] . The set of all automorphisms of is a subgroup of the symmetric group and we denote it by. More treatment of linear codes can be found in the book [2] .

Ideally, we would like the rate to be high, in order to be able to send a large number of errors. The

rate of a DW-code approch zero very quickly when the code length increase: as shown

in Figure 1 where and, so.

It is more convenient to use the DW-codes in the construction of other codes by using some technic of construction and not to use it alone.

2. Distinct weight codes

Definition 1 A linear binary code of length is said to be a Distinct Weight Code, (in short: DW-code), if

the weight mapping:, is one to one, that is whenever,.

The simplest example of such codes are the repetition codes. Later we shall give more nontrivial examples. Let a DW-code of length and dimension. Since the number of element of is, then we have. In the sequel we fix our interest to the extreme case, in which we give a construction.

Proposition 2 Let such that. Then every family of words such that is linearly independent.

Proof. Suppose on the contrary that are not linearly independent, then we have a linear combi-

nation, where some is nonzero. Let be the maximal integer such that. Then

, and. Now taking the weights leads to:

a contradiction.

Now we give a construction of a DW-code.

Let be a nonzero integer and. Take the canonical basis of. Put,

then clearly. By the proposition 2, the code-words are linearly independent and

generate a linear code that we denotes by. It also seen that, whenever. This

implies that.

A generator matrix of looks like:

Proposition 3 The -code is a DW-code.

Proof. Since the cardinal of is, it suffices to show that wt: is onto.

Let, then can be written in the base 2, where. Set,

then.

Up an equivalence we have the following result:

Theorem 4 There exists only one distinct weight -code, moreover such code is Boolean subring of

.

Proof. Let be such a code and take code-words, each has weight. These are linearly independent and form a basis of. Next we show that,. Otherwise, there exists a

least integer such that for some. Since, one have.

Multiplying by yields. Now consider the word,

On the other hand, if we

consider, then. Thus hence

a contradition. This means that, if. Since, and is a

basis of, then is a Boolean ring.

Now we define a linear mapping by. Then,. If

, then. This implies that

is an isometry between and, and by the extension theorem of MacWilliams, see [3] or [4] , there

exists a permutation, such that.

Example 5 and

By using the software Q-extension, see [5] we show, up to equivallence, that among six equivallence classes

the unique DW-code of parametters is the code of generator matrix. It is clear

that it is equivallent to the code of generator matrix. Just swap the second and third

rows and then apply the permutation.

Theorem 6 Let, Diophantine equations for which

, , ,

have a unique solution which is the k-uplet.

Proof. is clearly a solution of the Diophantine equation which satisfies the conditions

(1). Assume that for some and, then where

and. We can assume without loss of generality that

. So by the uniqueness of Development of any integer less than or equal

in binary basis, the equality leads to a contradiction. So the solution

satisfies the conditions (2).

Conversely, Let a solution of the equation satisfying (1)-(2). We can

take, elements of such that and,

, , , , are linearly independent. The

condition (2) means that the code of generator matrix is a dw-code. On after Theorem 1.3, the

condition (1) implies that there exists an invertible by matrix and a permutation matrix

such that where and

is the generator matrix of the code. It is clear that is of the form:

where or 1, and we have. So we have

, and then we have, by the

uniqueness of development of in binary basis. By (1) we have

, then we have:, Kronecker symbol.

Since, we have, and finally we have

.

Remark 7 Without the conditions (1) and (2), Diophantine equations have different solutions. For all

note that there is no DW-self-dual code. Indeed, if not, we will have, wich is impossible.

3. classification and automorphism group of DW-Codes

3.1. Automorphism Group: thegeneral case

We consider, without loss of generality, that a generator matrix of a DW-code has no zero columns. Indeed, if this is the case, the zero columns are omitted and we consider the obtained DW-code. This assumption is made in the entier paper. We study the automorphism group of DW-codes. We first notice the following:

Proposition 8 Let any basis of an DW-code. Then

.

Moreover, if any generator matrix of, then is an automorphism of, if and only if, is an automorphism of the binary matrix.

Proof. Clear.

Proposition 9 The automorphism group of any DW-code is nontrivial of even order.

Proof. Let be a generator matrix of a DW -code. We may suppose that all columns of are

nonzero. The columns of are taken among a set of columns. Suppose that all columns of are distincts, since, then the columns of are the distinct nonzero vectors of and will be the simplex code, which is clearly not DW. This contradiction shows that at least 2 columns of are identical. Now the transposition of these two columns gives an automorphism of.

We deduce that the dual code of a DW-code has a non-trivial automorphism group and has minimum distance.

We consider the general case. The action of automorphism group on the set

of columns of a generator matrix defined by: for all in and

in, splits all the columns of into disjoint orbits. The orbits each formed of a single

column, they are the columns fixed by the group. We set if no orbit is formed of a single

column and then it is clear that since since can not be trivial. The other orbits

are, ,. We set, if and

, , therefore, we have precisely.

Up to equivalence, we can consider that the code $mathcal $ is of generator matrix

rows of, such that.

Since is a DW-code, then for each for each we have

. So we have. We therefore deduce that:,

. So each orbit consists of equal columns.

The following theorem legitimate the idea of giving a definition to the 3-tuple

which we call signature of the DW-code and we denote.

We give here the full classification of such a code in several cases.

Theorem 10 If two DW-codes and are equivalent then they have the same signatures:

.

Proof. Let and two equivalent DW-codes of parameters. So such as.

We have. Let be a generator matrix of the code. Under the action of the

automorphism group we can assume that is of the form where

, and .

So we have and then

which is an orbit of the column under the action of on

the generator matrix of the code. similarly we have

which is an orbit of the column under the action of on the generator matrix. Thus

and have the same number of ponctual orbits, the same number of non-ponctual orbits and the two orbits

and on the one hand and and on the other hand have the same number of columns. we

conclude that the two codes and have the same Signature.

3.2. Classification

3.2.1. Case 1: and

We have

Theorem 11 If is an DW-code without punctual orbits and if the number of non

punctual orbits is equal to the dimension of the DW-code then the code is equivallent to a DW-

code of generator matrix

whith and t₁ = d is the minimal distance of

.

Proof. After a series of permutations and elementary operations on rows of we can make the first line of

the first orbit formed only by ones and all other rows are null all other bits of the first row of the

generator matrix are zero. Otherwise the first line of another orbit will be formed only by 1 s. And a series

of permutations and elementary row operations can make null all the other rows of this orbit so.

This is a contradiction since two orbits are disjoint. We obtain a generator matrix of an equivalent code denoted

by the same sign. It is easy to see that is a generator matrix of a DW-code

without punctual orbits and the number of orbits is equal to the dimension of this DW-code

and This allows for reasoning by induction. We obtain a generator matrix of an equivalent code

.

It is clear that we have, , , and,

since implies the existence of a punctual orbit.

Remark 12 In this case, up to equivallence, each DW-code admits the system as

orthogonal basis:, , , such as

, , , and.

Example 13 Consider the DW-code of generator matrix

. It is equivallente to the code of generator matrix

, , , ,

Corollary 14 Let two DW-codes and without punctual orbits and the number of their orbits

is equal to their dimension. Then the codes and are equivallent if and only if.

The converse of Theorem 11 is true under an additional condition.

Theorem 15 Let an code of generator matrix as in the last remark. If:

, , we have

then is a DW-code of minimum distance for which and.

Proof. Clear.

Corollary 16 The number of equivalence classes of DW-codes such as, and

equals the number of solutions of the Diophantine equations

satisfying the following conditions

, , ,.

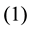
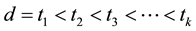
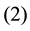
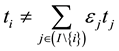
Proof. Let the application that maps each equivalence class represented by the matrix to the

t-tuple solution of the Diophantine equation as described in Theorem 11. This application is

clearly a bijection between the set of equivalence classes and the set of solutions of the Diophantine equation satisfying conditions (1) and (2).

3.2.2. Case 2: and

Theorem 17 If is an DW-code with punctual orbits and if the number of non

punctual orbits is equal to the dimension of the DW-code then the code is equivallent to the

DW-code of generator matrix with and

.

Example 18 Consider the DW-code of generator matrix

. It is equivallente to the code of generator matrix

, , , ,

We have since and are equivallente.

The converse of this theorem is true under an additional condition. Let an of generator matrix

with: and. are f different

columns which are also different from all unitary columns, , ,.

For each, denote by the weight of the sum of all the jth rows where of the

matrix

For all denote by the weight of the ith row of the matrix. So by

setting the numbers we have the following result, let an code of generator matrix

as described in theorem 17 we have:

Theorem 19 If for all, for all and for all, we have

then the code is a DW-code.

Let an DW-code such as, and. We have

different way to the choice of fixed columns. For each value of and for the -th choice of fixed

columns we denote by, the number of solutions of the Diophantine equations

which satisfy the following conditions

, , ,

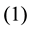
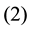
So we have the following result.

Theorem 20

The number of equivalence classes of DW-codes with and a given such that

and equals the number.

The number of equivalence classes of DW-codes with, and equals

the number.

Example 21 By using the result of the last theorem and the Q-extension software, We show that there exist

Only 4 DW-code up to equvallence verifying. Indeed and we have:

・ For the set of possible columns taken in the following order are:

,

So the number of DW-codes with, and is.

・ For the set of possible columns taken in the following order are:

So there is no DW-codes with, and since.

・ For the set of possible columns taken in the following order are:

So there is no DW-codes avec, and since.

・ For the set of possible columns taken in the following order are:

, , ,.

So there is one DW-codes such as, and since.

We deduce that there is only four DW-codes, among 98 equivalence classes, satisfying

since

3.2.3. Case 3: and

We have necessarily.

Theorem 22 If is an DW-code without punctual orbits and if the number of non punc-

tual orbits is different from the dimension of the DW-code then

and the code is equivallent to the DW-code of generator matrix

with.

Example 23 The DW-code of generator matrix is equivallent to the code

of generator matrix, , , , , ,.

In this case two DW-codes with the same signature are not necessarily equivalent as shown in the following example:

Example 24 Let the DW-code of generator matrix and the DW-code of generator matrix such as and are not equivalent and

,

.

We have.

3.2.4. Case 4: and

We can have two cases or

Theorem 25 If is an DW-code with punctual orbits and if the number of non

punctual orbits is greater than the dimension of the DW-code then the code is equivallent to the

DW-code of generator matrix with.

Example 26 The DW-code of generator matrix is equivallent to the code

of generator matrix , , , , , ,

Theorem 27 If is an DW-code with punctual orbits and if the number of non

punctual orbits is lower than the dimension of the DW-code then the code is equivallent to the DW-code of generator matrix

with.

Example 28 The DW-code of generator matrix is equivallent to the code

of generator matrix , , , ,.

Remark 29 Self-orthogonality.

A code which is equivalent to a self-orthogonal code is also self-orthogonal. The property of self- ortho- gonality is then an invariant of the equivalence of codes. We then have the following points:

・ If or (and)then, up to equivalence, a generator matrix of the code is of the form where is not an empty submatrix. If the code is self-othogonal then. So

and then we have:

and and then

and then where.

and then

finally and and then

・ If and the code is self-orthogonal if and only if for all.

3.3. Determination of the Automorphism Group

Theorem 30 The automorphism group of a DW-code of signature is isomorphic to

the group direct product.

Proof. Let be a generator matrix of the code. We can assume that is of the form

where, and

.

For, let, let for all. Clearly, the subsets

form a partition of. Now let.

Clearly the are subgroups of and each is isomorphic to and for all

. Since forall, , it follows that the are subgroups of.

Now we are going to show that is the inner direct product

If, and, , then.

Let, then applying this equality to each yields,.

Now let. Since, the are globally invariant under. Let the permutation

defined by, if, and elswhere. Then it is clear that, and this finishes the proof.

Example 31

・ Consider the DW-code of generator matrix. It is equivallente to the code

of generator matrix , , , , ,

and

・ Consider the DW-code of generator matrix. It is equivallente to the code

of generator matrix , , , , and

Acknowledgements

The authors would like to thank the refrees for their helpful suggestions and remarks.

Conflicts of Interest

The authors declare no conflicts of interest.

References

[1]	Bouyukliev, I. (2007) About the Code Equivalence, Advances in Coding Theory and Cryptology. In: Shaska, T., Huffman, W.C., Joyner, D. and Ustimenko, V., Eds., Series in Coding Theory and Cryptology, World Scientific Publishing, Vol. 3, 126-151.
[2]	MacWilliams, F.J. and Sloane, N.J.A. (1977) The Theory of Error-Correcting Codes. Elsevier-North-Holland, Amsterdam.
[3]	MacWilliams, F.J. (1962) Combinatorial Problems of Elementary Abellan Groups. Ph.D. Dissertation, Harvard University, Cambridge.
[4]	Bogart, K., Goldberg, D. and Gordon, J. (1978) An Elementary Proof of the MacWilliams Theorem on Equivalence of Codes. Information and Control, 37, 19-22. http://dx.doi.org/10.1016/S0019-9958(78)90389-3
[5]	Bouyukliev, I.G. (2007) What Is Q-Extension? Serdica Journal of Computing, 1, 115-130.