Keywords:Analytic Functions, Integral Operators, General Schwarz Lemma

1. Introduction
Let 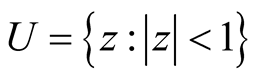 be the unit disk and A be the class of all functions of the form
be the unit disk and A be the class of all functions of the form
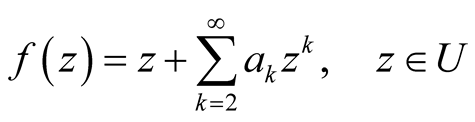 (1)
(1)
which are analytic in U and satisfy the conditions
 .
.
We denote by S the class of univalent and regular functions.
In order to derive our main results, we have to recall here the following univalence conditions.
Theorem 1.1. [1] (Becker’s univalence criterion).
If the function f is regular in unit disk U,  and
and
 , (2)
, (2)
then the function f is univalent in U.
Theorem 1.2. [2] If the function g is regular in U and  in U, then for all
in U, then for all  the following inequalities hold
the following inequalities hold
 (3)
(3)
and
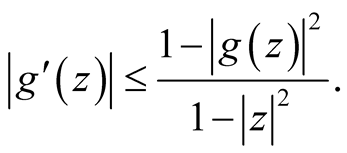
the equalities hold in case 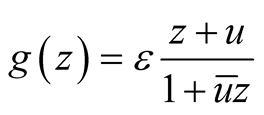 where
where  and
and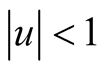 .
.
Remark 1.3. [2] For , from inequality (3) we obtain for every
, from inequality (3) we obtain for every 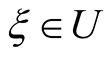
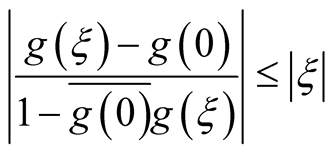 (4)
(4)
and, hence
 (5)
(5)
Considering  and
and , then
, then
 for all
for all .
.
2. Main Results
In this paper we study the univalence of the following general integral operators:
 (6)
(6)
where  and
and ,
,
 (7)
(7)
where  and
and .
.
Theorem 2.1. Let ,
,  ,
,  ,
,  ,
,  ,
,  ,
,  If
If
 (8)
(8)
for all , for all
, for all  and
and
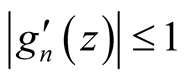
 (9)
(9)
 (10)
(10)
where

then the function
 (11)
(11)
is in the class S.
Proof. We have ,
, 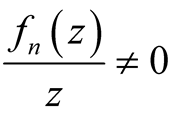 , for all
, for all  and
and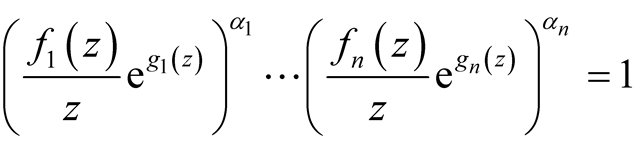 , when
, when .
.
Let us consider the function:
 (12)
(12)
From (6), we have:
 (13)
(13)
and
 (14)
(14)
From (13) and (14), we have:
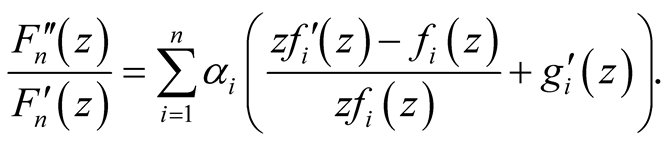
Using relations before the function h has the form:
 (15)
(15)
We have:
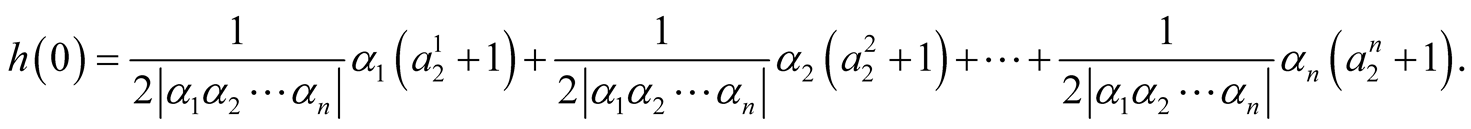
By using the relations (15), (8) and (9), we obtain:
 (16)
(16)
 (17)
(17)
Applying Remark 1.3 for the function h, we obtain:
 (18)
(18)
From (18), we get:
 (19)
(19)
for all .
.
Let us consider the function: 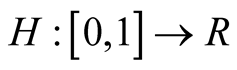
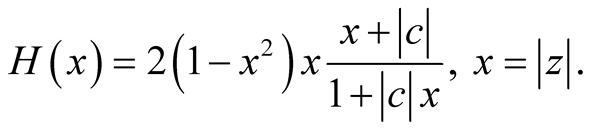
Since , it results:
, it results:
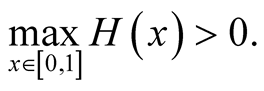
Using this result and the form (19), we have:
 (20)
(20)
for all .
.
Applying the condition (10) in relation (20), we obtain:
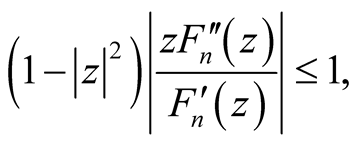
for all  and from Theorem 1.1, we have
and from Theorem 1.1, we have .
.
Corollary 2.2. Let  be a complex number and the functions
be a complex number and the functions ,
, 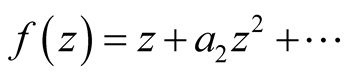 ,
,  ,
, .
.
If
 (21)
(21)
for all  and the constant
and the constant  satisfies the condition:
satisfies the condition:
 (22)
(22)
then the function
 (23)
(23)
is in the class S.
Proof. We consider 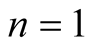 in Theorem 2.1.
in Theorem 2.1.
Remark 2.3. For ,
,  ,
,  and
and  in relation (11), we obtain the integral operator
in relation (11), we obtain the integral operator
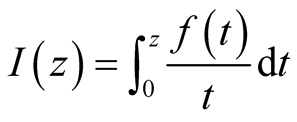 , introduced by J. W. Alexander in [3] .
, introduced by J. W. Alexander in [3] .
Remark 2.4. For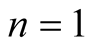 ,
,  ,
,  ,
,  in relation (6), we obtain the integral operator
in relation (6), we obtain the integral operator
 , defined and studied by V. Pescar in [4] [5] .
, defined and studied by V. Pescar in [4] [5] .
Remark 2.5. For , for all
, for all , we get the integral operator
, we get the integral operator ,
,  studied by D. Breaz, N. Breaz in [6] and D. Breaz in [7] .
studied by D. Breaz, N. Breaz in [6] and D. Breaz in [7] .
Theorem 2.6.
Let ,
, 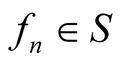 ,
,  ,
,  ,
,  ,
,  ,
, .
.
If
 (24)
(24)
for all , for all
, for all  and
and 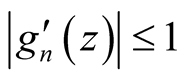
 (25)
(25)
 (26)
(26)
where

then the function
 (27)
(27)
is in the class S.
Proof. We have , for all
, for all  and
and , when
, when .
.
Let us consider the function:
 (28)
(28)
From (27), we have:
 (29)
(29)
and
 (30)
(30)
From (29) and (30), we get:
 (31)
(31)
Using relation (31) the function p has the form:
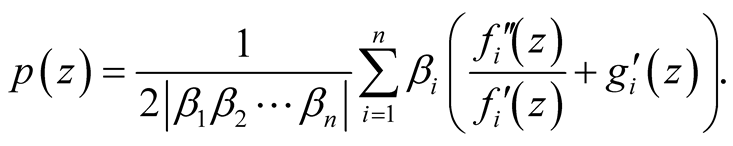
We have:

By using the relations (24), (25) and (28), we obtain:
 (32)
(32)
and
 (33)
(33)
Applying Remark 1.3 for the function p, we obtain:
 (34)
(34)
From (34), we get:
 (35)
(35)
for all .
.
Let us consider the function 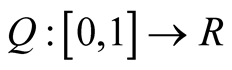
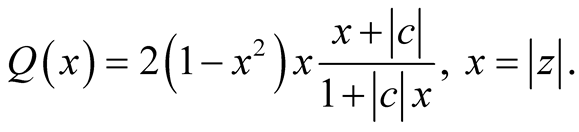
Since , it results:
, it results:

Using this result and the form (35), we have:
 (36)
(36)
for all .
.
Applying the condition (26) in relation (36), we obtain:

for all  and from Theorem 1.1, we have
and from Theorem 1.1, we have .
.
Corollary 2.7. Let 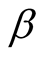 be a complex number and the functions
be a complex number and the functions ,
,  ,
, 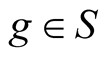 ,
, .
.
If
 (37)
(37)
for all  and the constant
and the constant 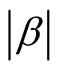 satisfies the condition:
satisfies the condition:
 (38)
(38)
then the function
 (39)
(39)
is in the class S.
Proof. We consider  in Theorem 2.6.
in Theorem 2.6.
Remark 2.8. For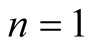 ,
,  ,
,  ,
,  in relation (27), we obtain the integral operator
in relation (27), we obtain the integral operator
 , defined and studied by V. Pescar in [8] [9] .
, defined and studied by V. Pescar in [8] [9] .
Remark 2.9. For  and
and  in relation (27), we obtain the integral operator
in relation (27), we obtain the integral operator
 , introduced and studied by N. Ularu and D. Breaz in [10] and [11] .
, introduced and studied by N. Ularu and D. Breaz in [10] and [11] .
Acknowledgements
This work was supported by the strategic project PERFORM, POSDRU 159/1.5/S/138963, inside POSDRU Romania 2014, co-financed by the European Social Fund-Investing in People.