1. Representation of Approximation Residual
For convenience we shall give scheme of representation of the approximation residual in general situation (see also [1]).
We consider a linearly independent system of columnvectors 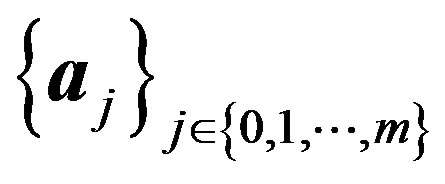 (where m is a natural number)
(where m is a natural number)
in the space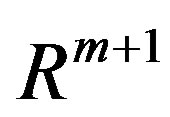 . The matrix
. The matrix  composed of these columns is denoted by
composed of these columns is denoted by
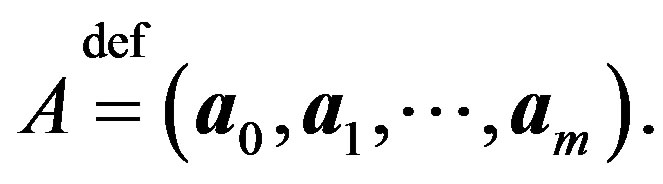 (1)
(1)
Let  be linear space.
be linear space.
Suppose that 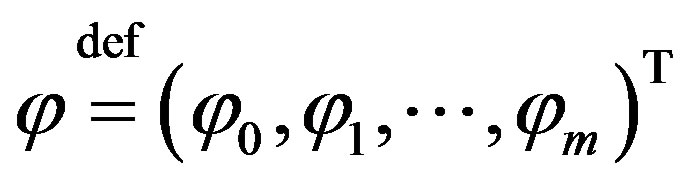 and
and
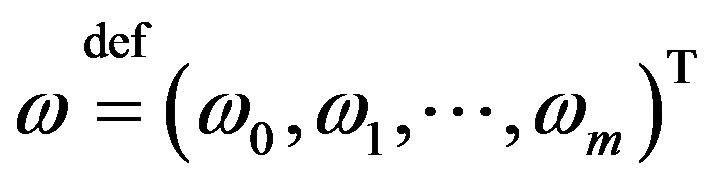 are columns with components belonging to the space
are columns with components belonging to the space ; assume the relation
; assume the relation
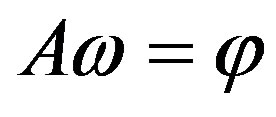 (2)
(2)
is valid; matrix A is defined by (1).
Let 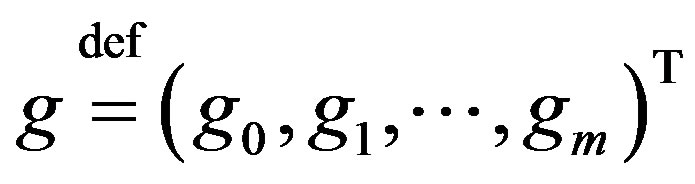 be vector with components
be vector with components
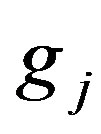 belonging to conjugate space
belonging to conjugate space .
.
For an element 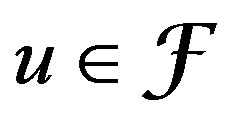 we consider a linear combination of elements
we consider a linear combination of elements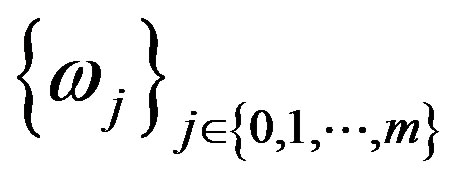 :
:
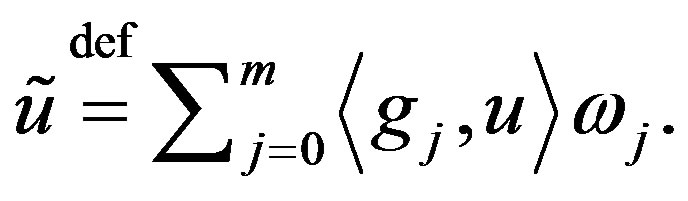 (3)
(3)
From (2) and (3) it follows that
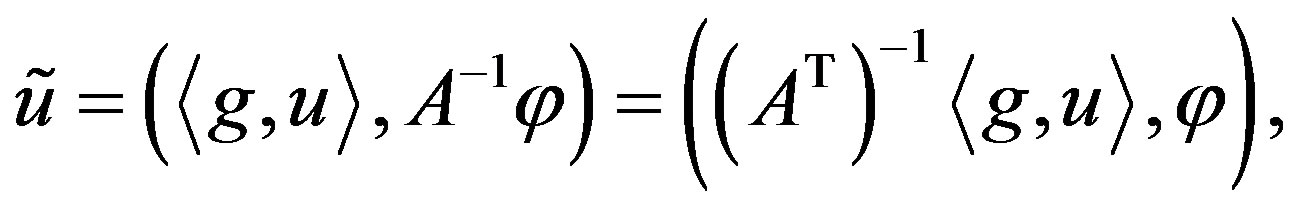 (4)
(4)
where 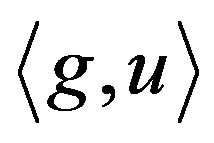 denotes the column-vector in
denotes the column-vector in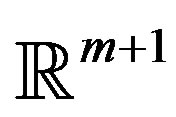 namely,
namely,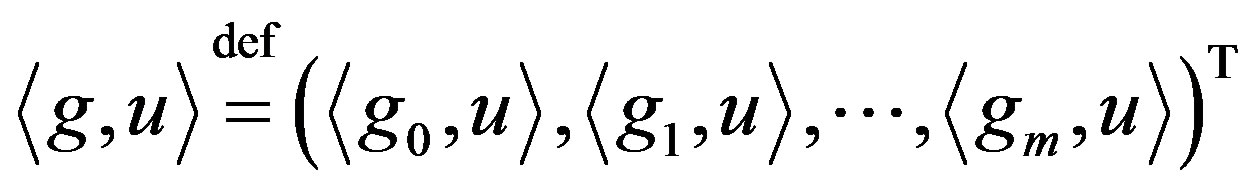 . The outer round brackets in (4) mean the inner product of
. The outer round brackets in (4) mean the inner product of 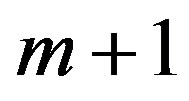 -dimensional vectors.
-dimensional vectors.
Theorem 1 The following relation holds:
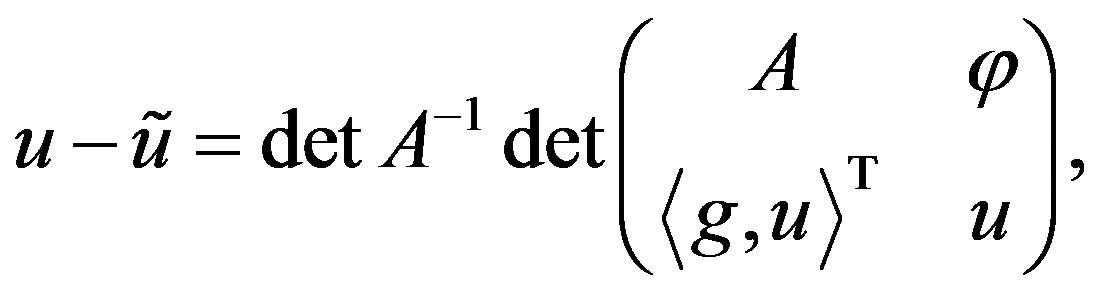 (5)
(5)
where the second factor on the right-hand side is the determinant of a block-matrix of order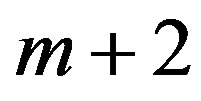 .
.
Proof By (4), we have 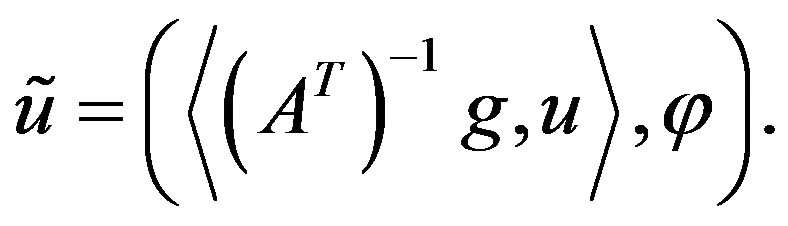 Hence
Hence
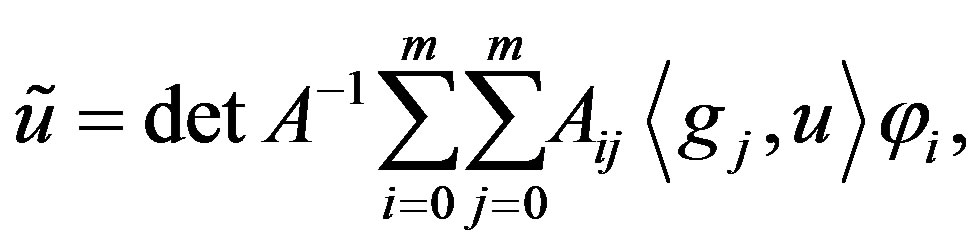 (6)
(6)
where 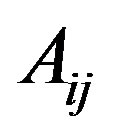 is the cofactor of an entry
is the cofactor of an entry 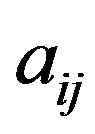 of the matrix
of the matrix . By (6), we can represent the difference
. By (6), we can represent the difference 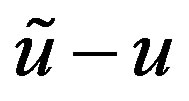 as the product of determinants, written as
as the product of determinants, written as
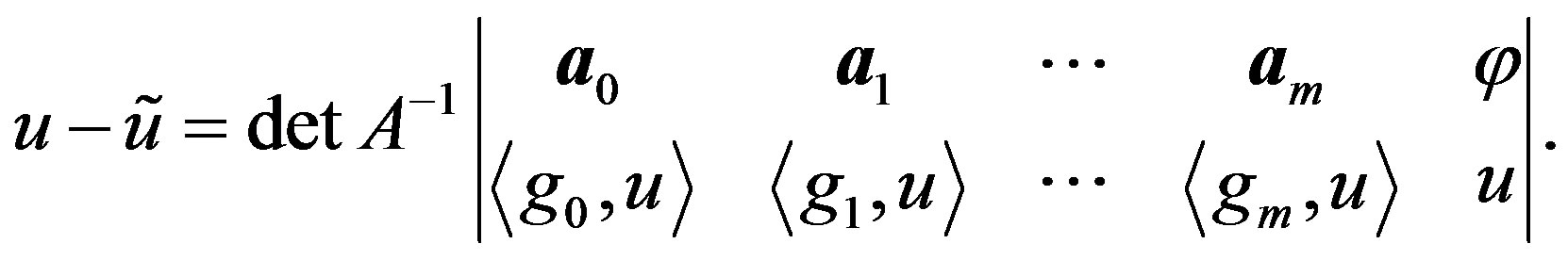 (7)
(7)
The equality (7) is equivalent to the equality (5).
2. Representation of the Remainder of Approximation by Elementary Hermite Type Splines
On 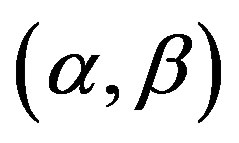 we consider a grid of the form
we consider a grid of the form
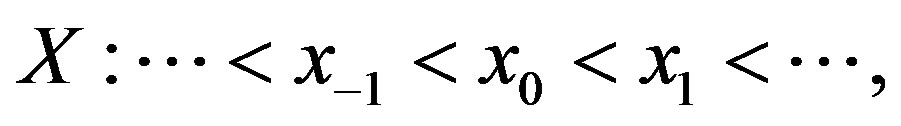
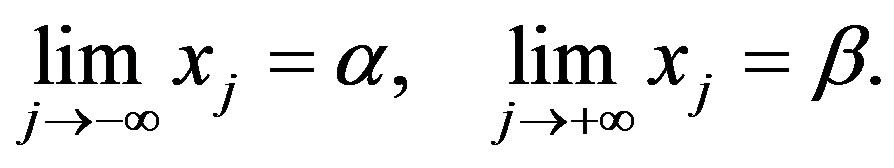
We set
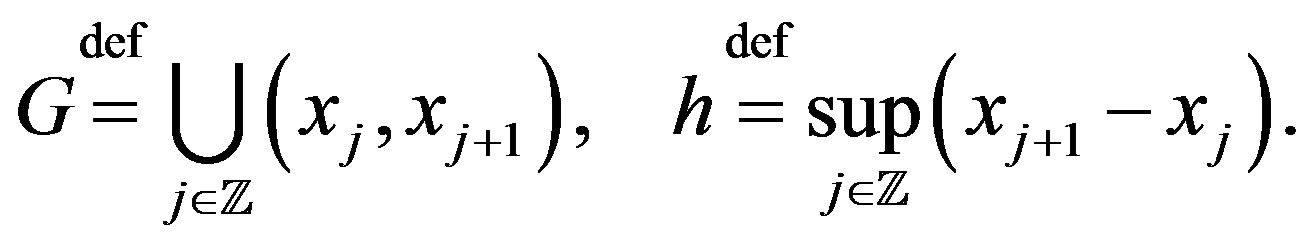
Let 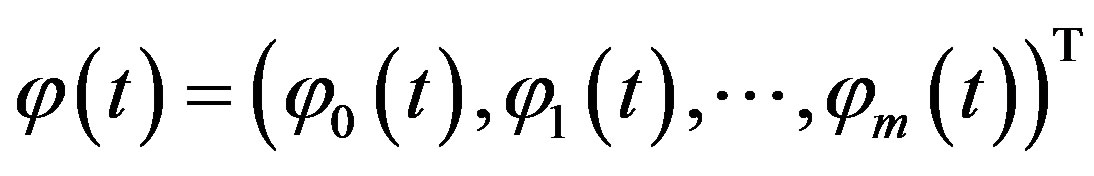 be
be 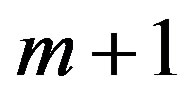 -component vector-function with components in
-component vector-function with components in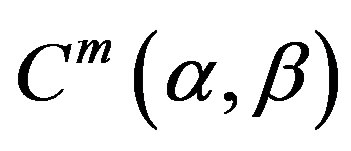 . We assume that Wronskian of the components is separated from zero.
. We assume that Wronskian of the components is separated from zero.
Consider function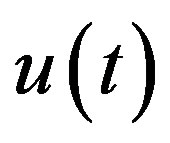 ,
, 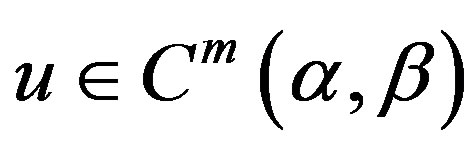 , and introduce notation
, and introduce notation
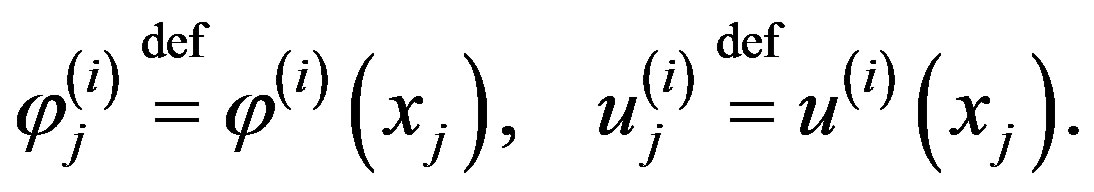 (8)
(8)
Let symbol 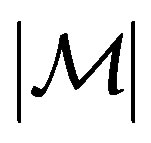 denote the number of elements of a set
denote the number of elements of a set .
.
We assume that natural numbers 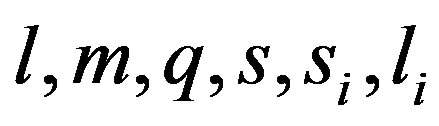 comply with relations
comply with relations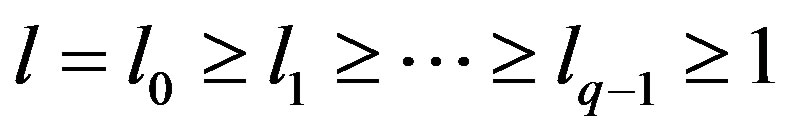 ,
, 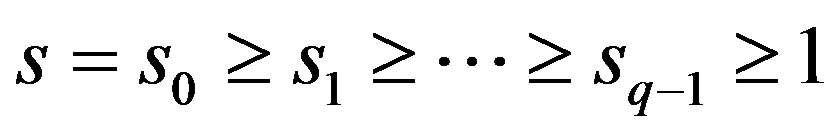 ,
,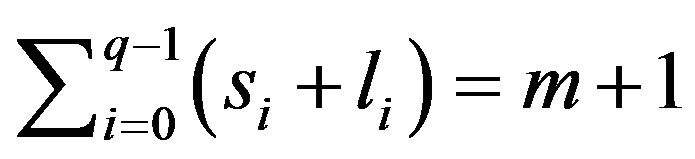 .
.
By definition, put
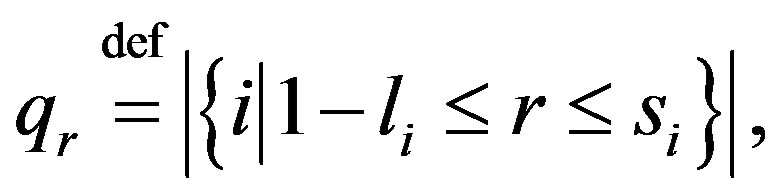
where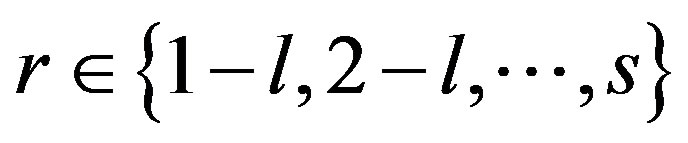 . Obviously
. Obviously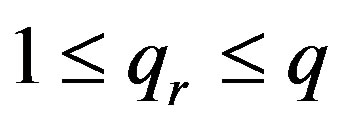 .
.
We introduce the functions 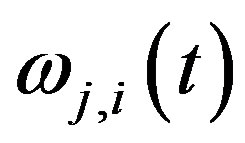 by the approximate relations
by the approximate relations
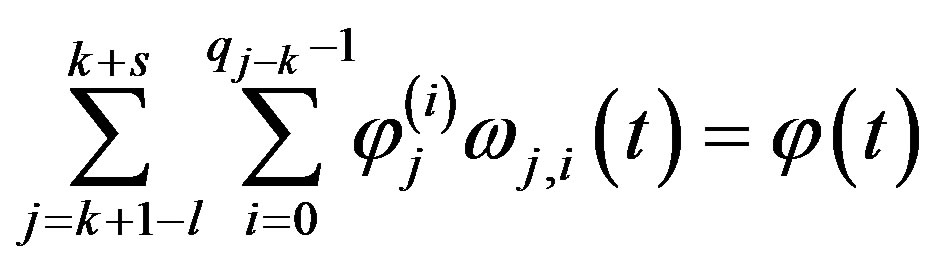 (9)
(9)
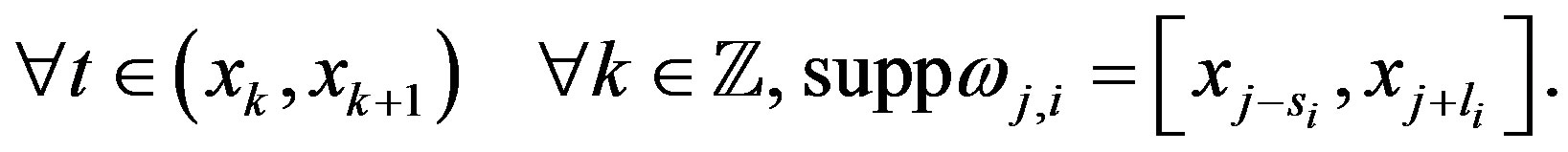
Consider square matrix 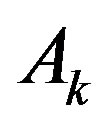 of the order
of the order 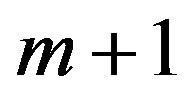 (see notation (8)),
(see notation (8)),
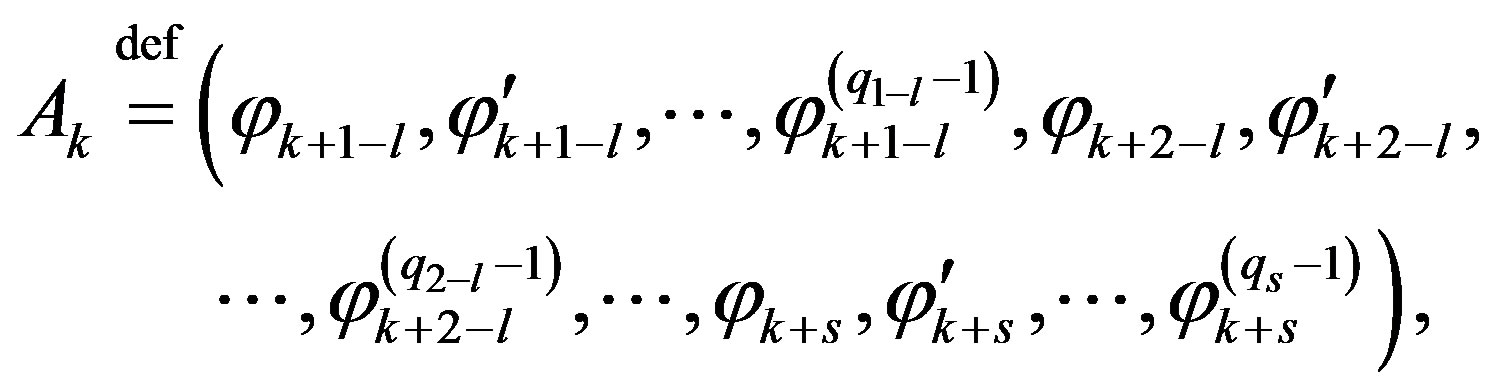
and vector-function
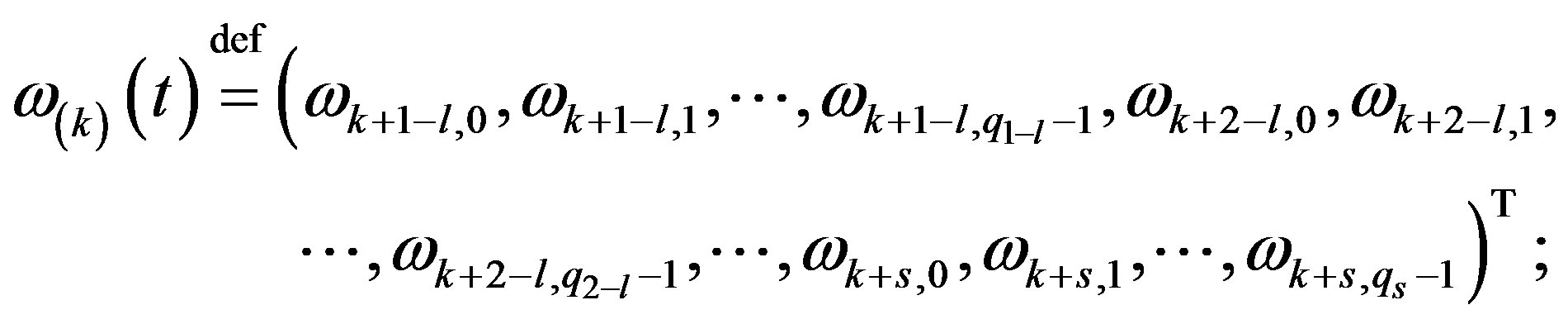
then the relations (9) may be rewritten as
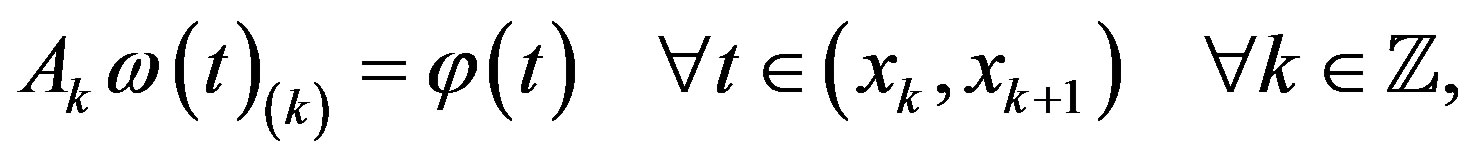
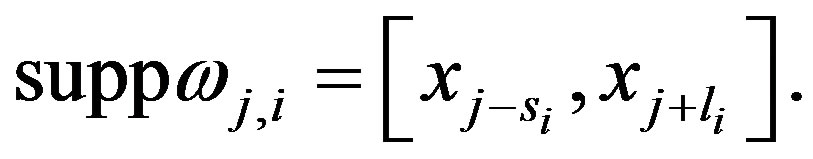
It can be proved (for example, see [2]) that the matrix 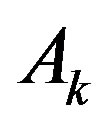 is invertible. Hence the functions
is invertible. Hence the functions 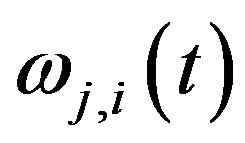 are defined uniquely and they are linear independent. If
are defined uniquely and they are linear independent. If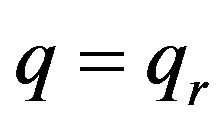 ,
, 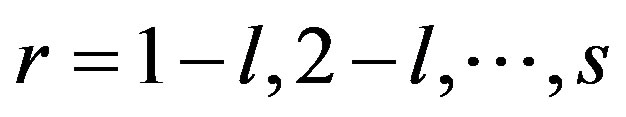 , then the functions
, then the functions 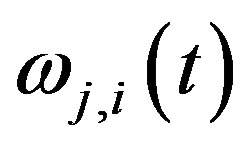 belong to
belong to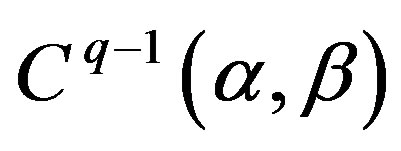 , and functional system
, and functional system 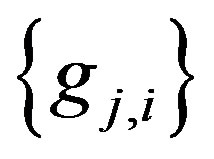 defined by formula
defined by formula
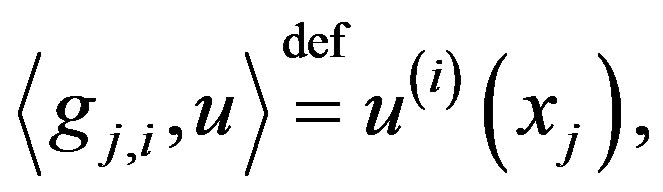
is biorthogonal to the system 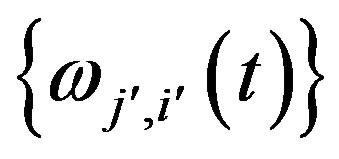 so that
so that

Rewrite the system (9) in the form
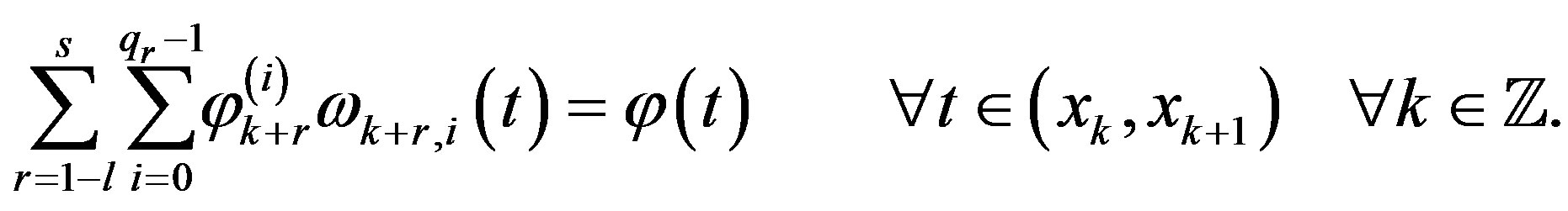 (10)
(10)
Under condition 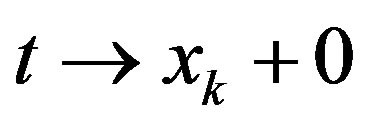 we have
we have
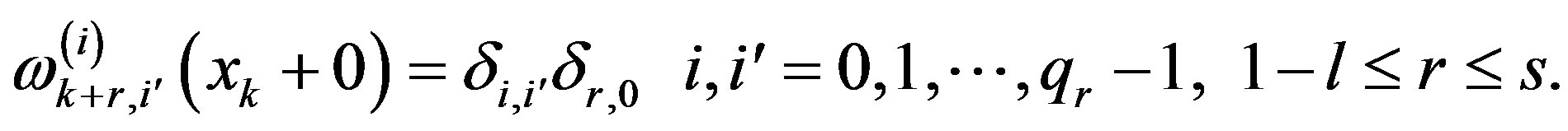
Analogously on the adjacent interval we get
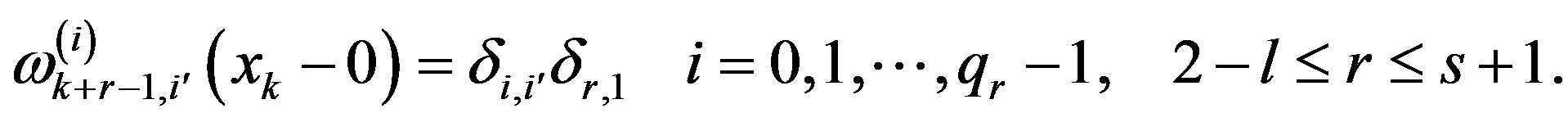
Discuss the linear space
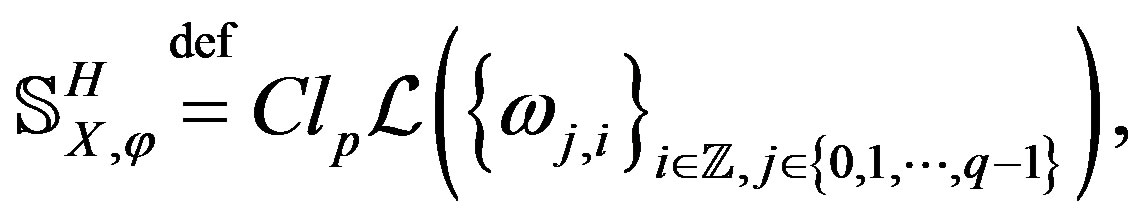
where 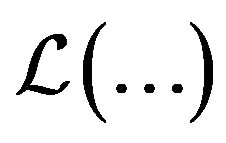 is the linear hull of the elements in the curly brackets and
is the linear hull of the elements in the curly brackets and 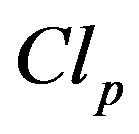 means the closure of the linear hull in the topology of pointwise convergence.
means the closure of the linear hull in the topology of pointwise convergence.
We call 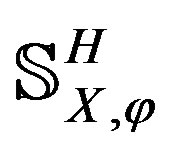 the space of elementary Hermite type
the space of elementary Hermite type 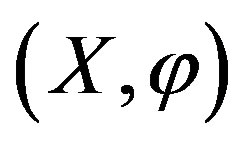 -splines.
-splines.
By definition, put
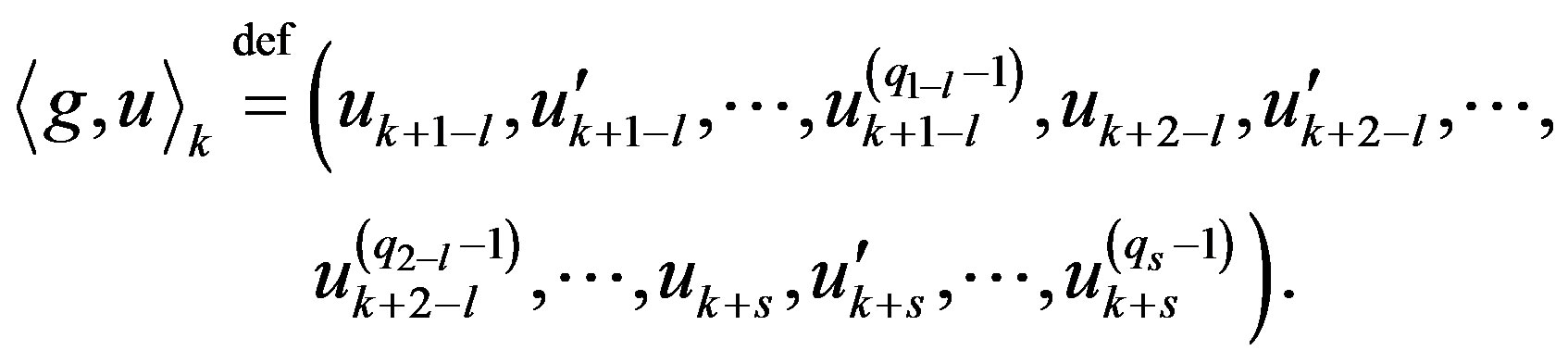
We consider the function 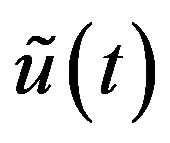 defined by
defined by
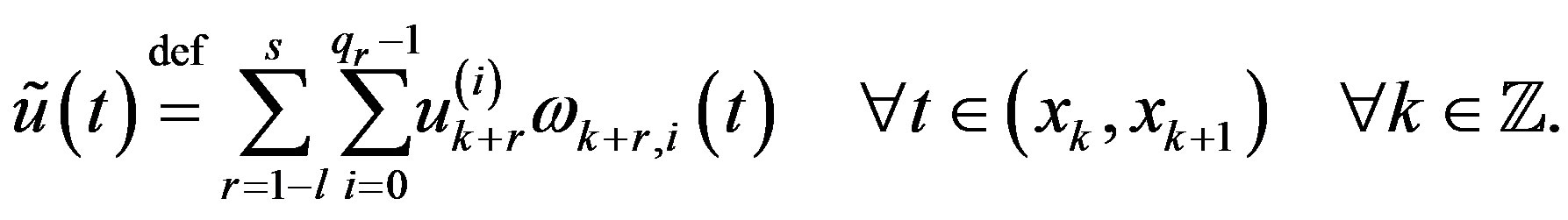 (11)
(11)
Theorem 2 For ,
, 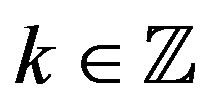 ,
,
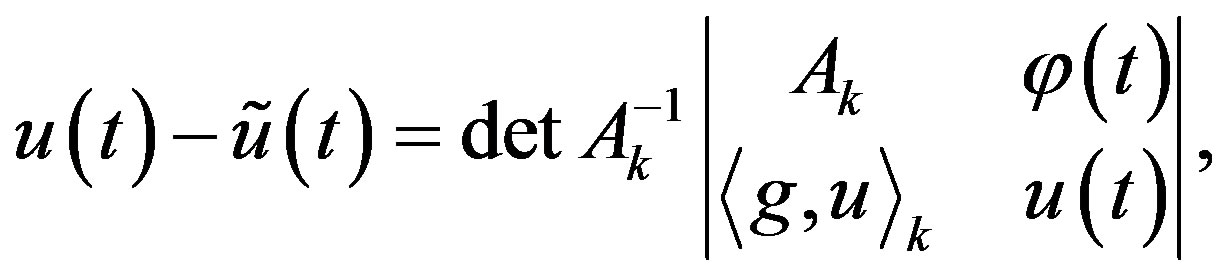 (12)
(12)
where the second factor on the right-hand side is the determinant of the square matrix of order 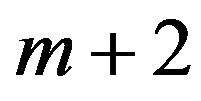 written in the block form.
written in the block form.
Proof We can obtain the identity (12) by expanding the second determinant of right part of (12) and by usage of the relations (10)-(11) (cf. [1]).
3. Some Auxiliary Assertions
Let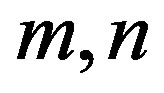 ,
, 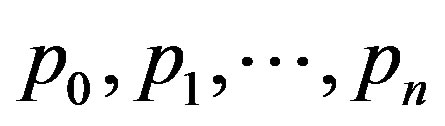 be natural numbers with property
be natural numbers with property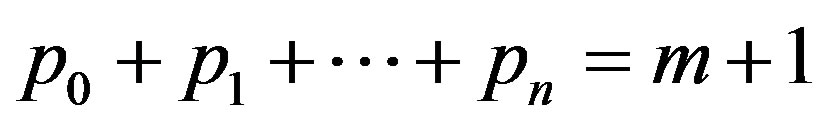 ; let
; let 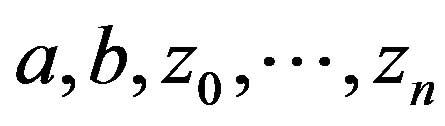 be real numbers, which comply with inequalities
be real numbers, which comply with inequalities  . Let us put
. Let us put
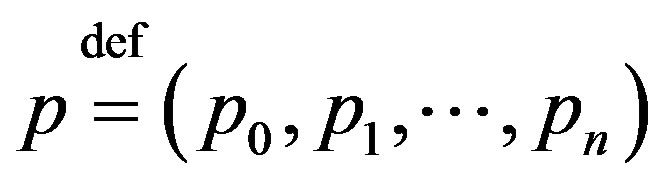 ,
,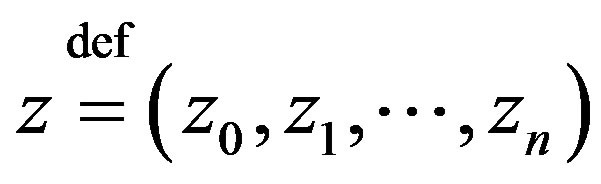 .
.
Lemma 1 For arbitrary 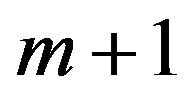 -component vector-function
-component vector-function 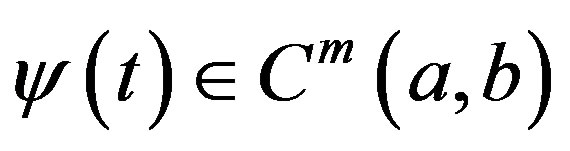 the representation
the representation
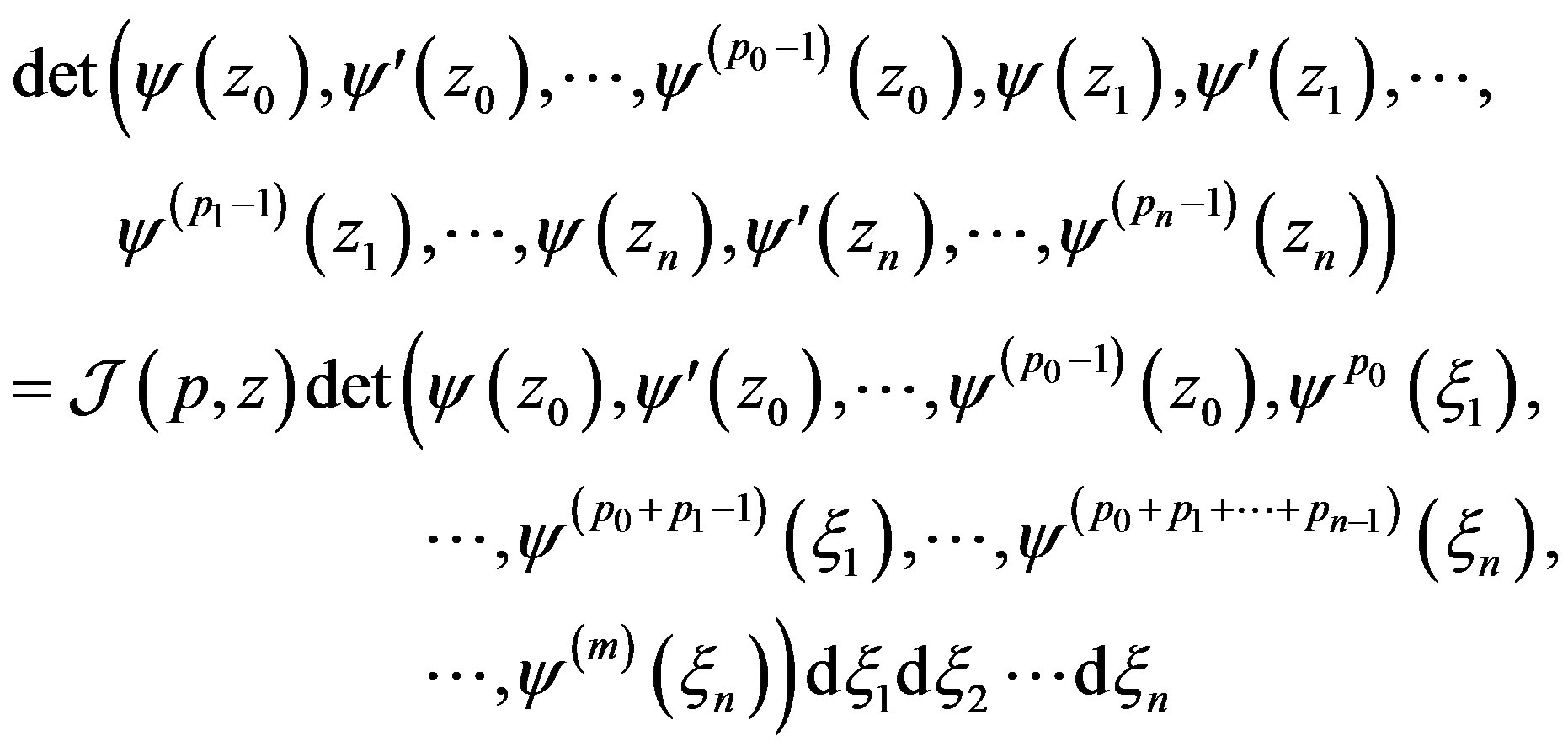 (13)
(13)
is valid; here 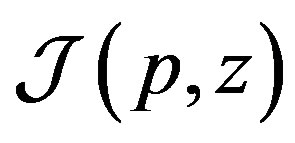 is a linear operator of integration over parallelepiped
is a linear operator of integration over parallelepiped
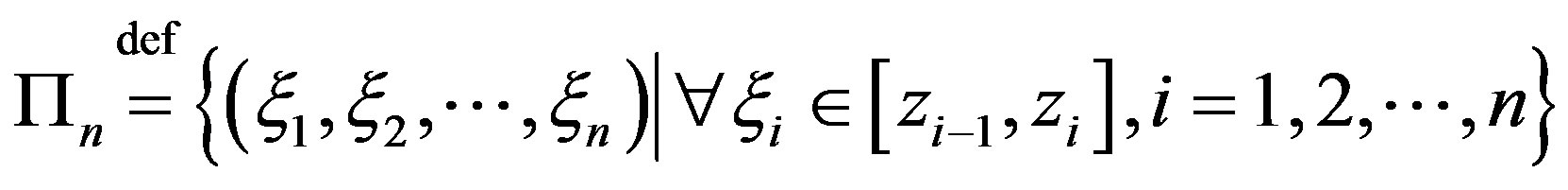
with nonnegative kernel.
Proof We consider the case 
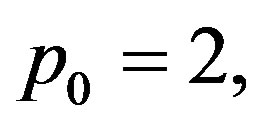
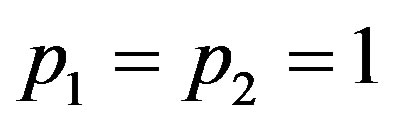 ,
,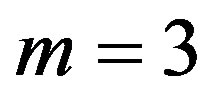 . Introduce value
. Introduce value 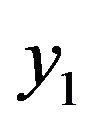 with property
with property 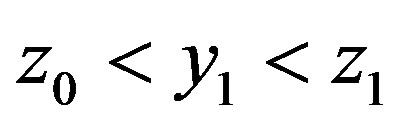 and use notation
and use notation
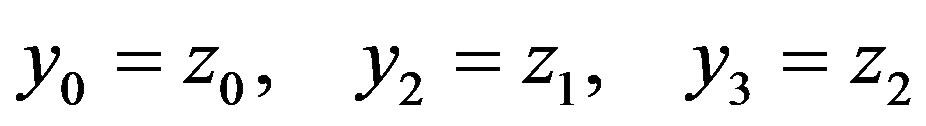 (14)
(14)
so that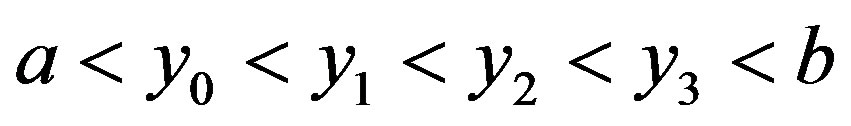 .
.
Using the additivity property of determinants and integrals and applying the Newton?-Leibnitz formula, we find
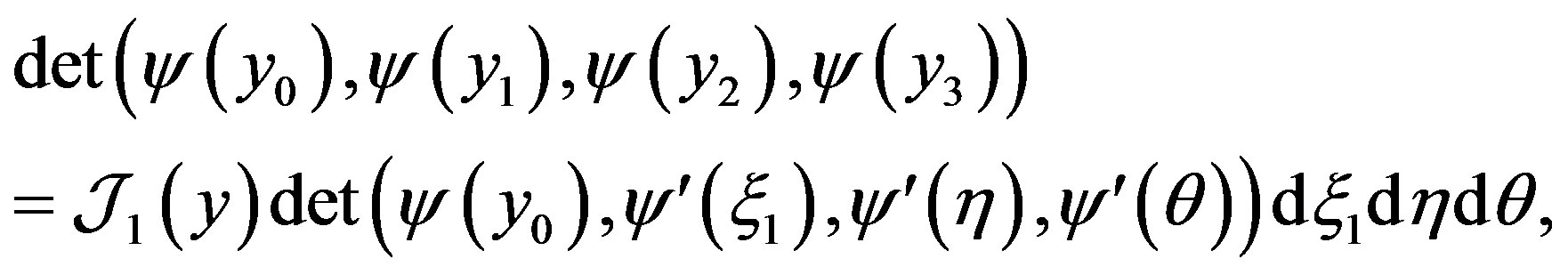
where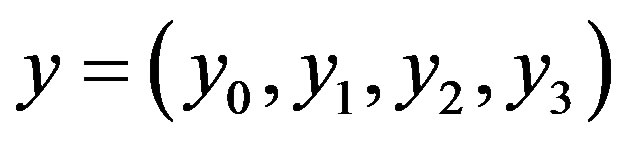 ,
,
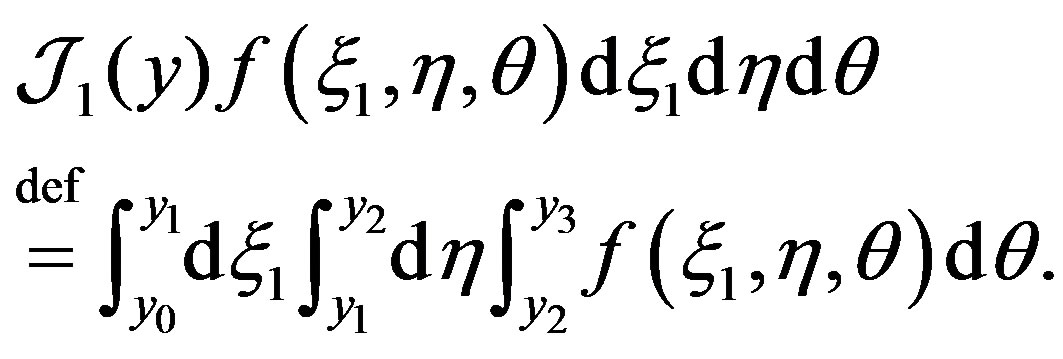 (15)
(15)
Similarly,
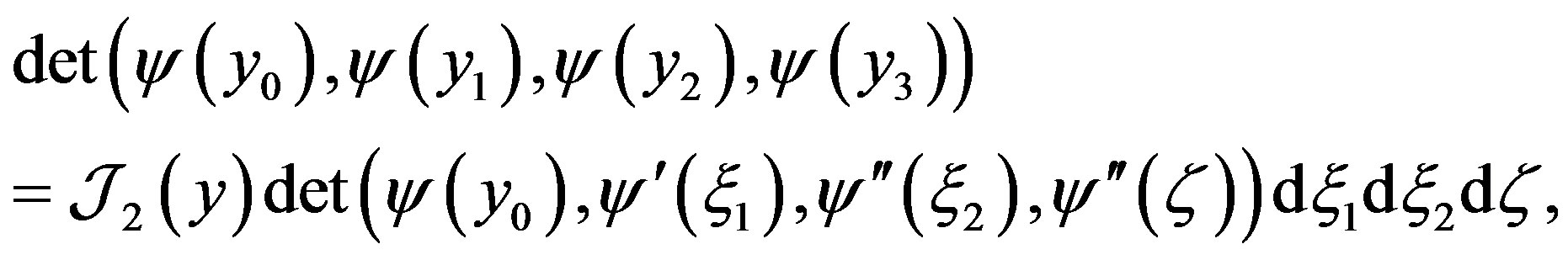
where
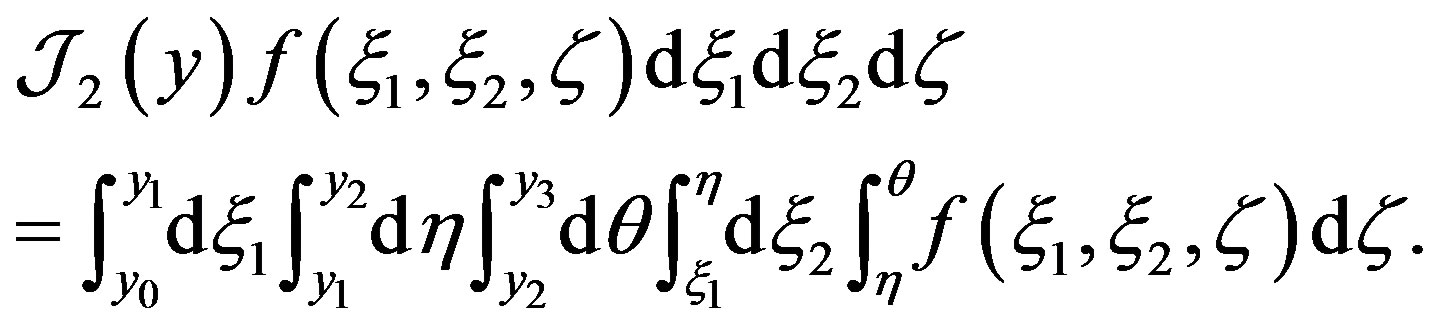 (16)
(16)
Finally
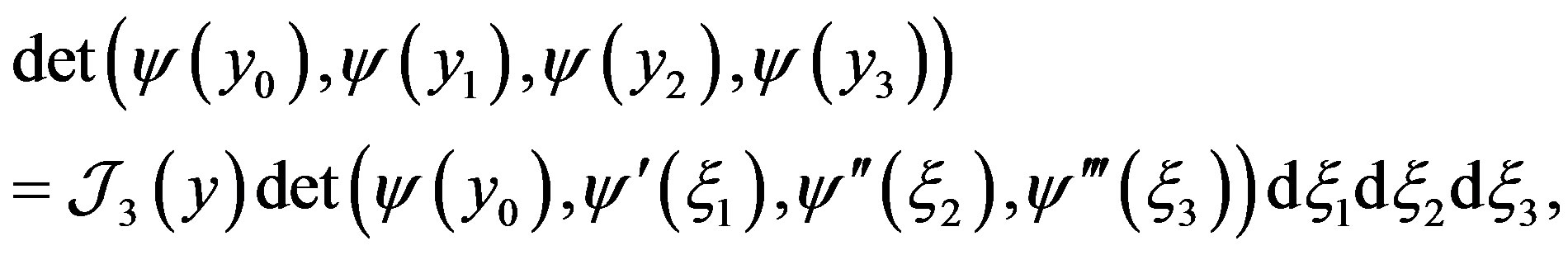
where
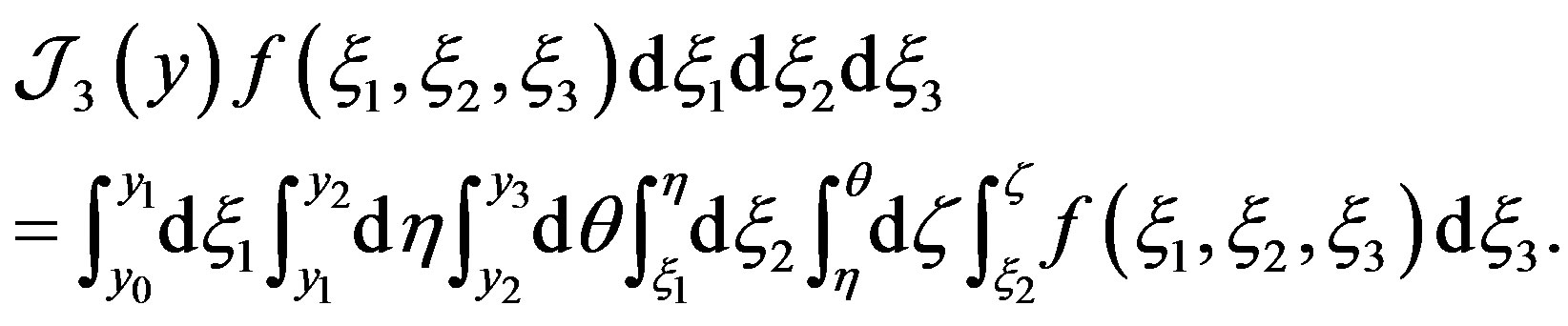 (17)
(17)
Integral operators 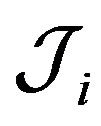 can be rewritten in the form
can be rewritten in the form
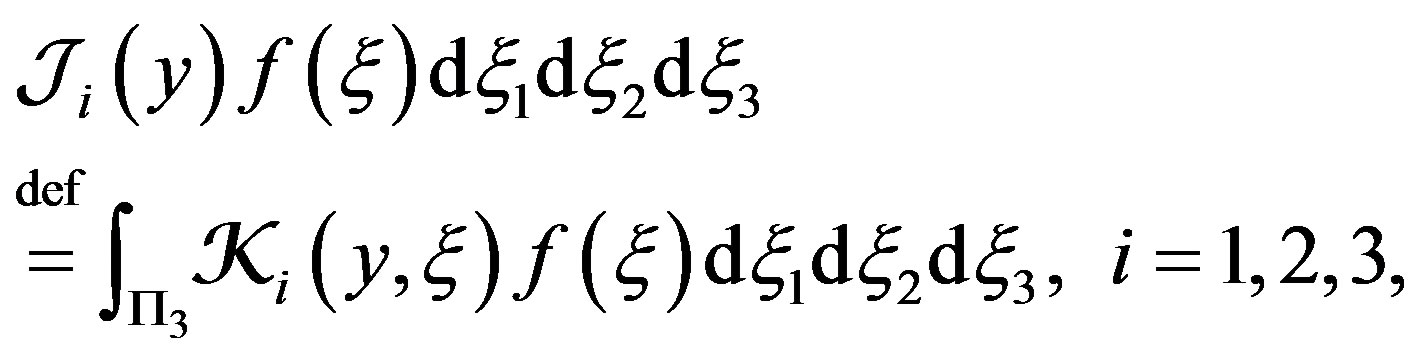
where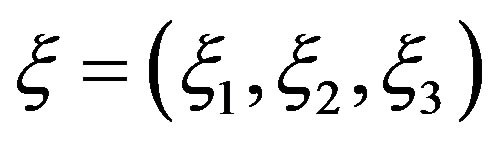 , and
, and
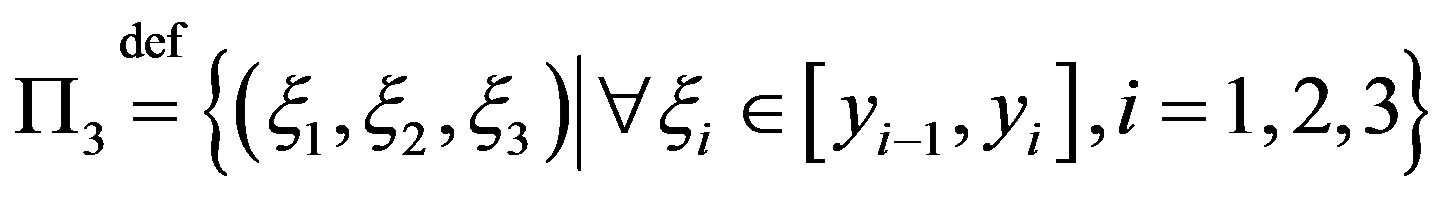 .
.
It is obvious that
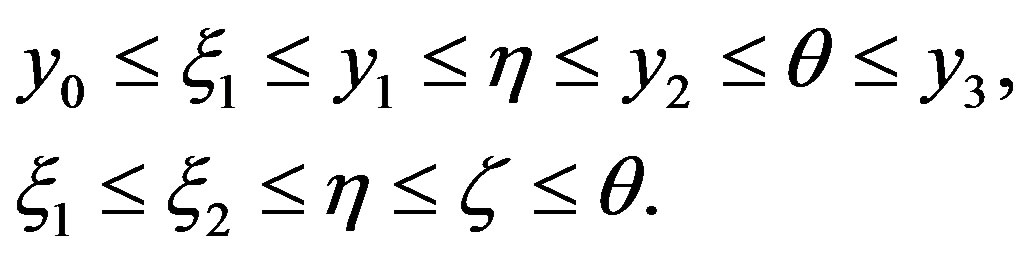 (18)
(18)
Since the lower limit is no more than the upper one in the integrals in (15)-(17), the result of integration is nonnegative for any nonnegative continuous function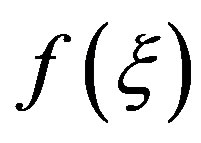 . Hence the integral operations
. Hence the integral operations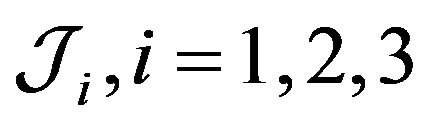 , have nonnegative kernels By (17) we have
, have nonnegative kernels By (17) we have
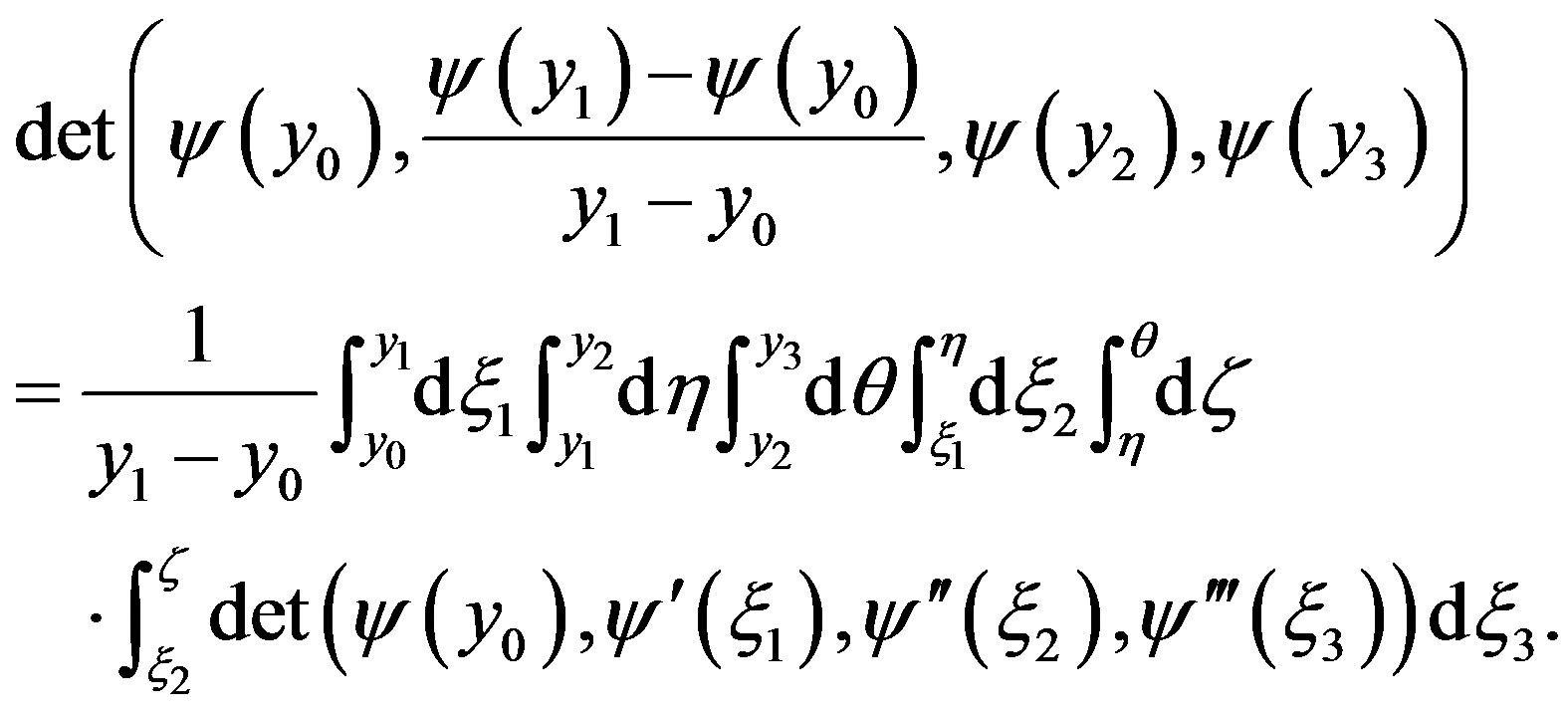 (19)
(19)
Recall that vector-function 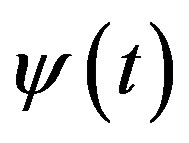 is continuously differentiable in neighborhood of the point
is continuously differentiable in neighborhood of the point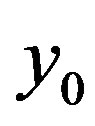 , and passaging to limit as
, and passaging to limit as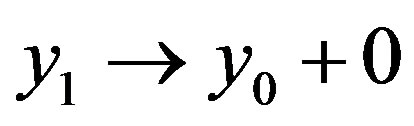 , we get
, we get
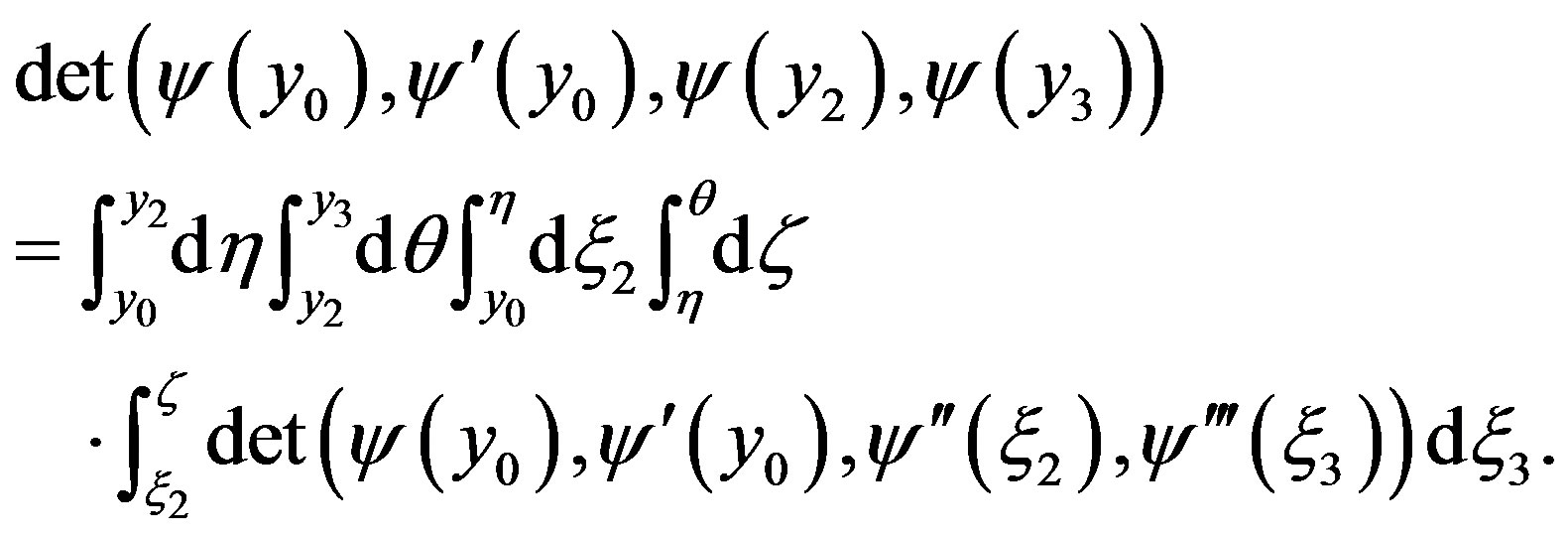 (20)
(20)
It follows easily that relation (20) can be written in the form
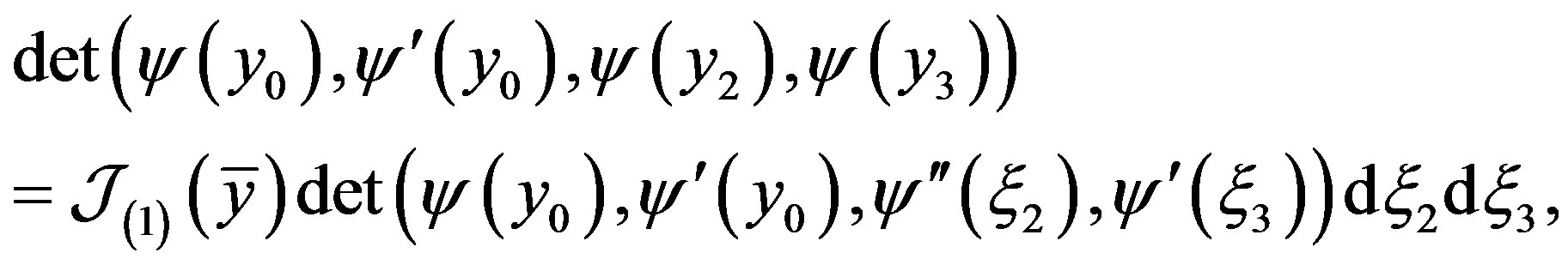
where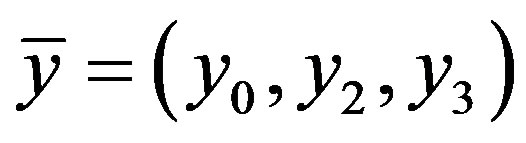 , and the operator
, and the operator 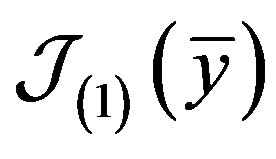 is defined by identity
is defined by identity
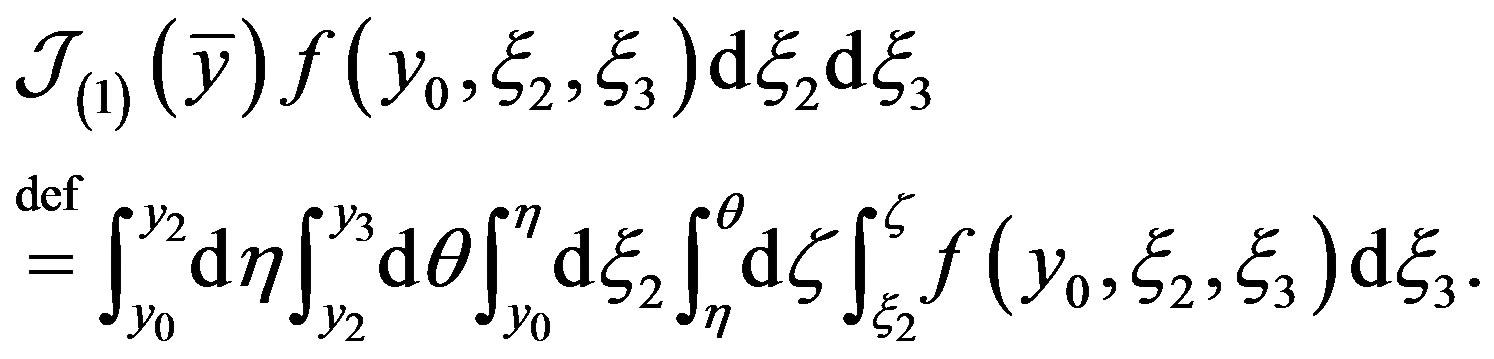 (21)
(21)
By relations (18) and (21) we see that the integral operator 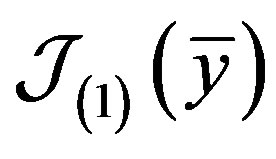 may be represented in the form
may be represented in the form
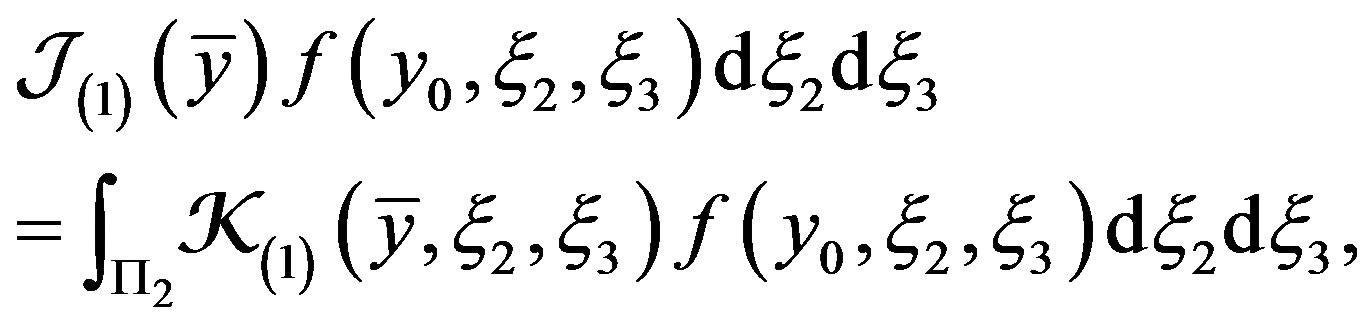
where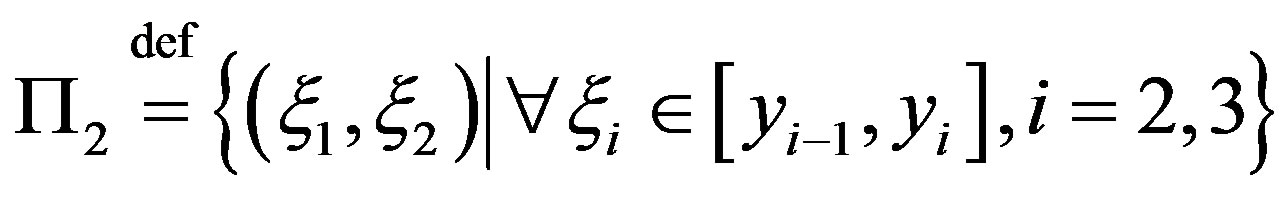 , and
, and 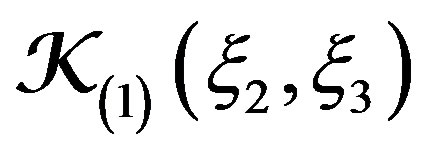 is nonnegative function Taking into account (14), we obtain
is nonnegative function Taking into account (14), we obtain 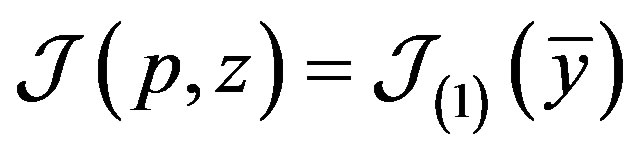 , where
, where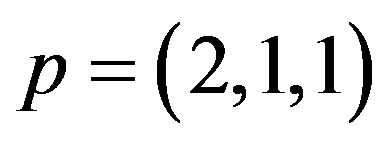 ,
, 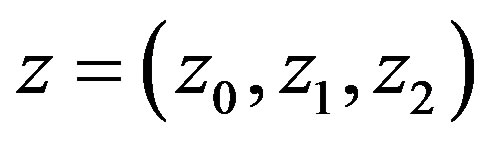 ,
,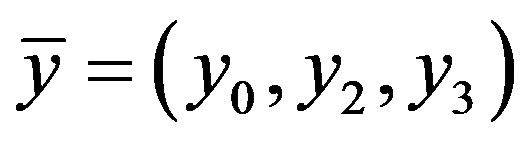 . Thus the assertion is true in discussed case.
. Thus the assertion is true in discussed case.
Now consider the case of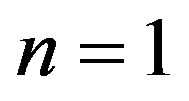 ,
, 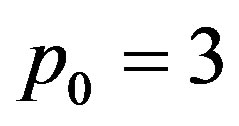 ,
,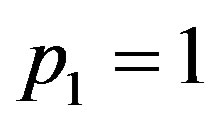 .
.
Let 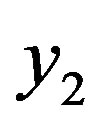 is new variable,
is new variable,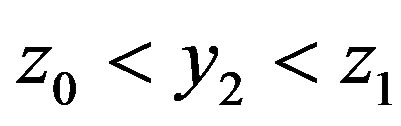 ; by definition put
; by definition put
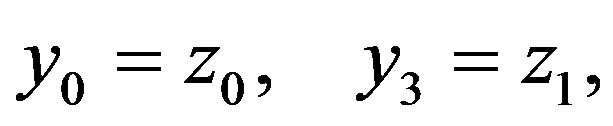 (22)
(22)
so that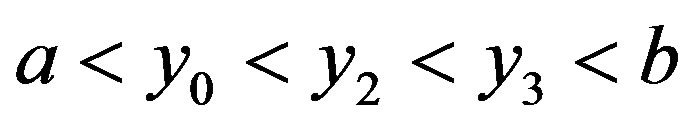 .
.
Under condition  according to Taylor formula we have
according to Taylor formula we have
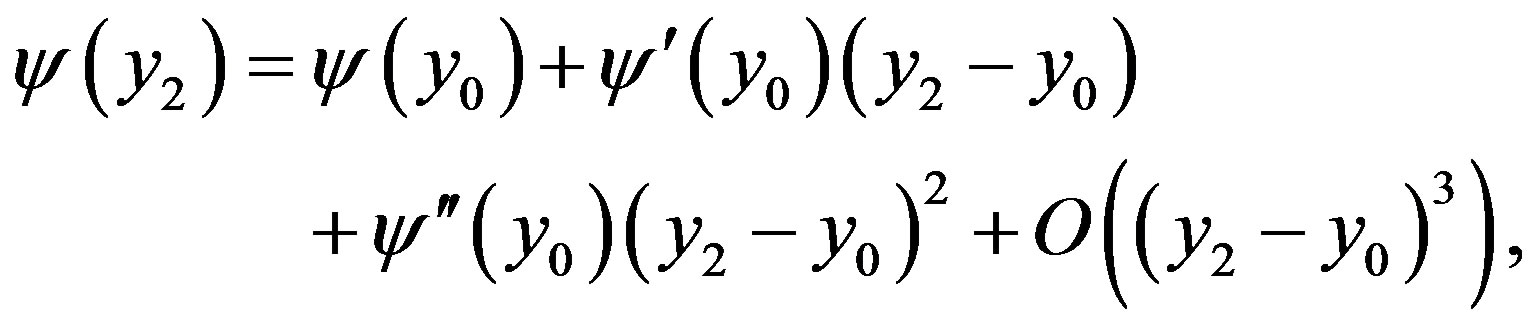
whence we get
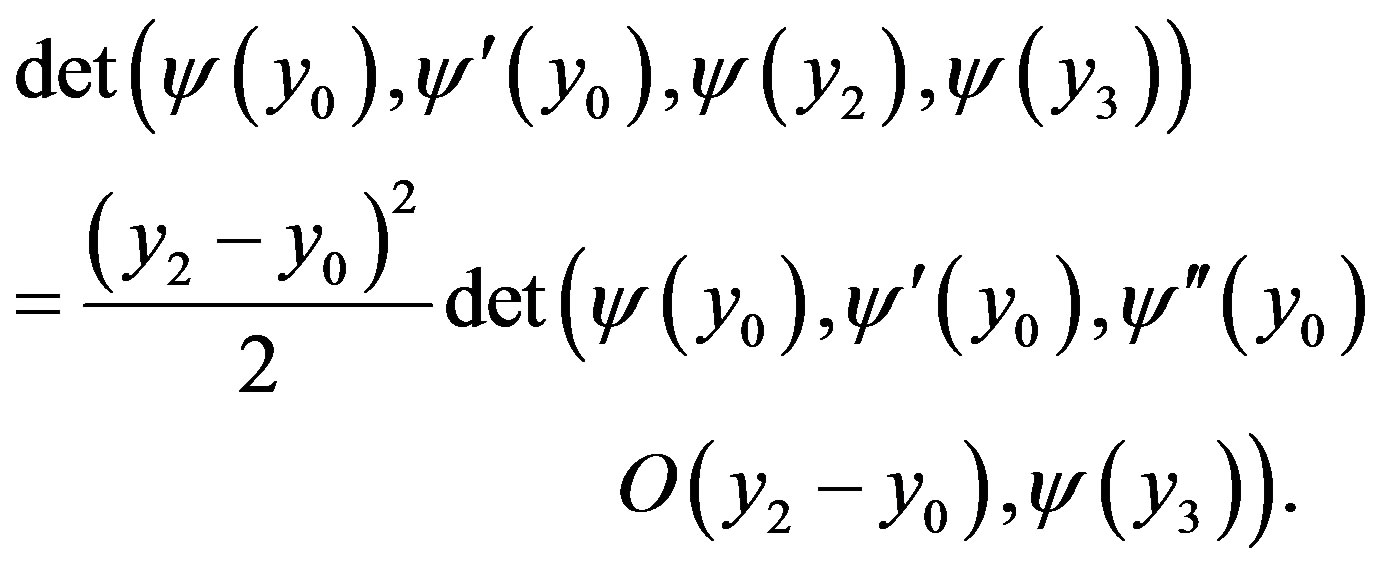
Thus by (21) we obtain
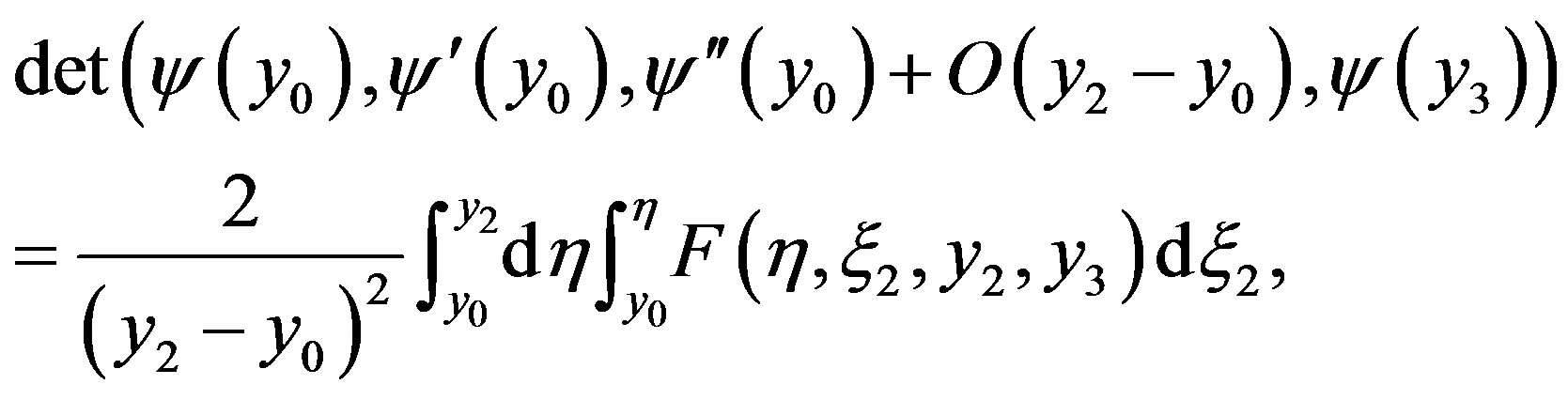
where
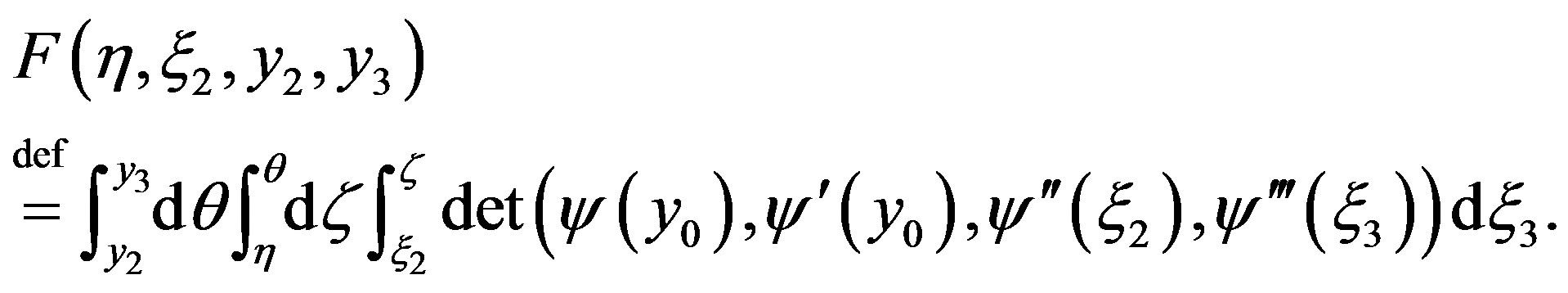 (23)
(23)
It follows in the standard way that
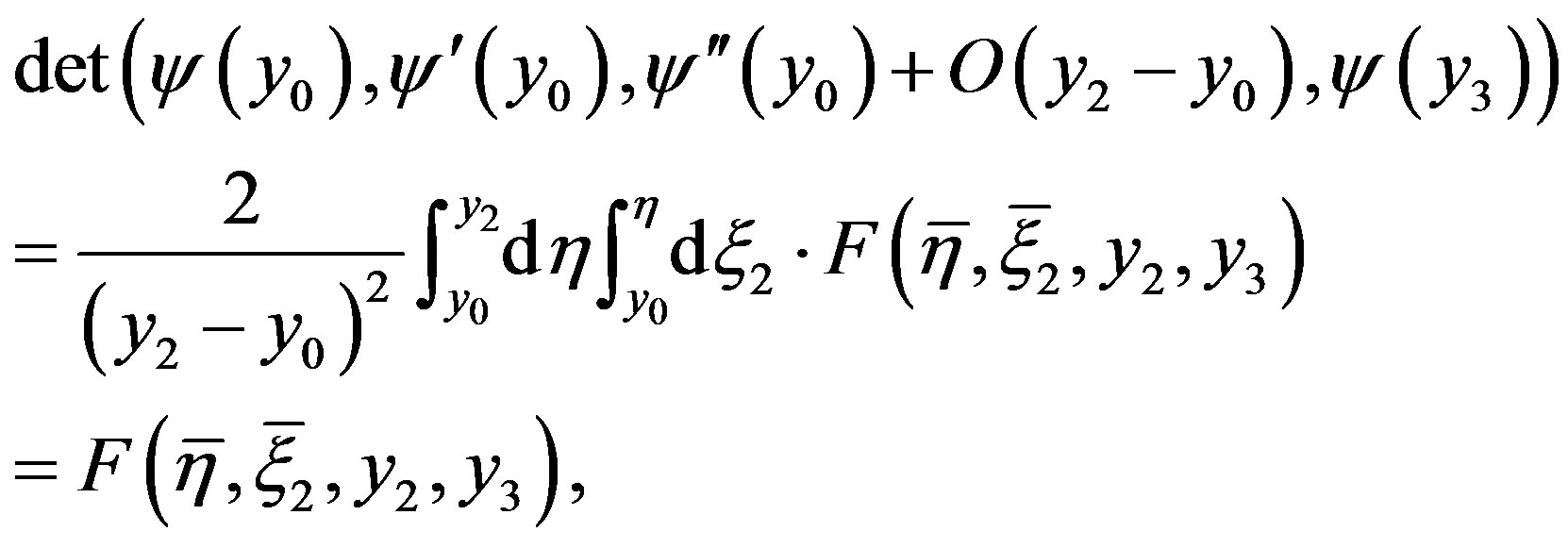
where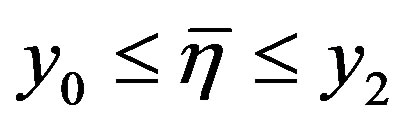 ,
,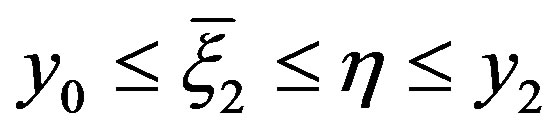 .
.
Passaging to limit under  we obtain
we obtain
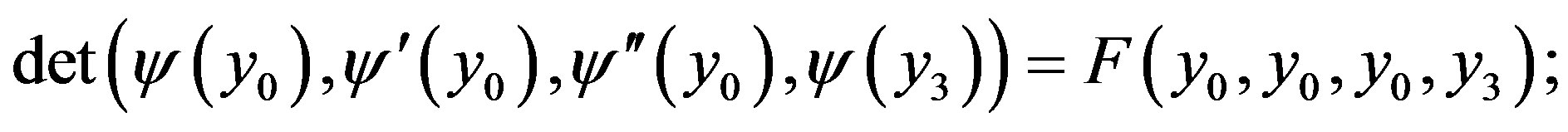
taking into account (23), we rewrite the formula in the form
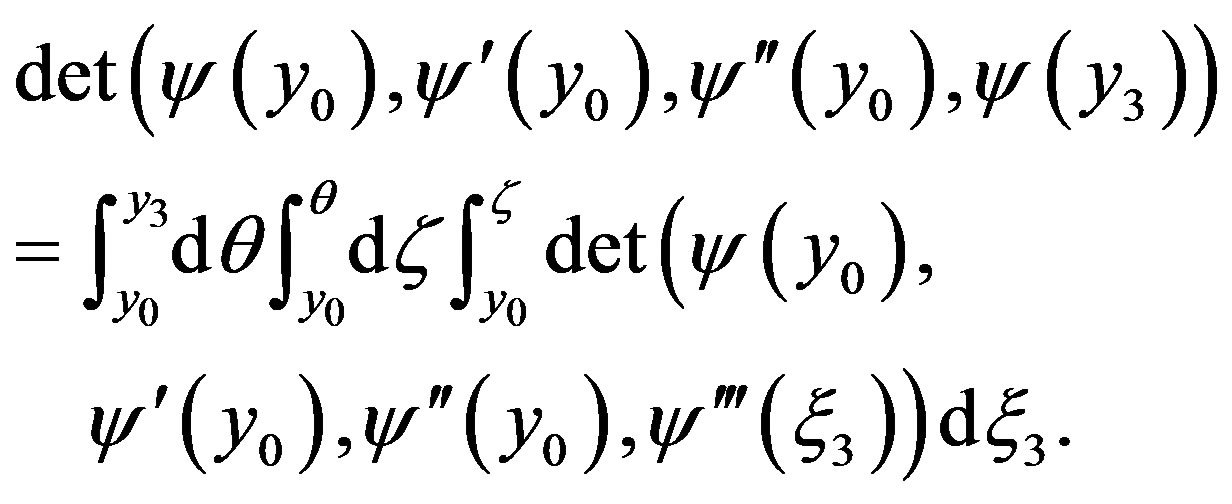
Thus
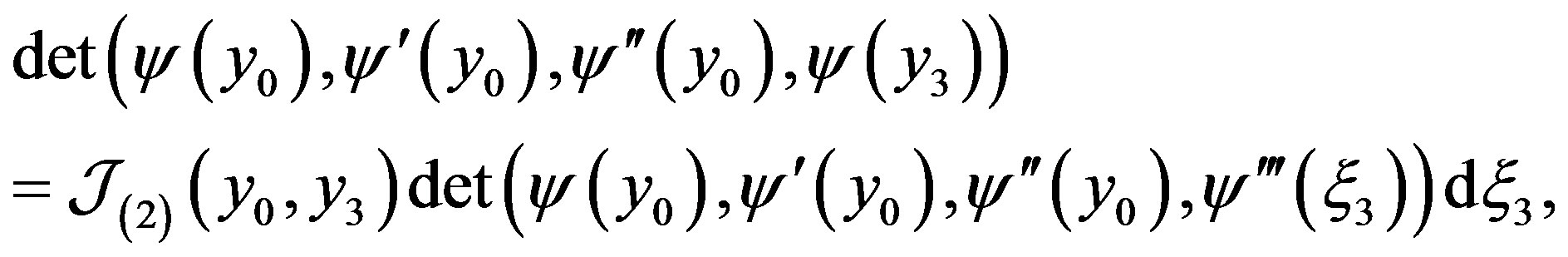
where
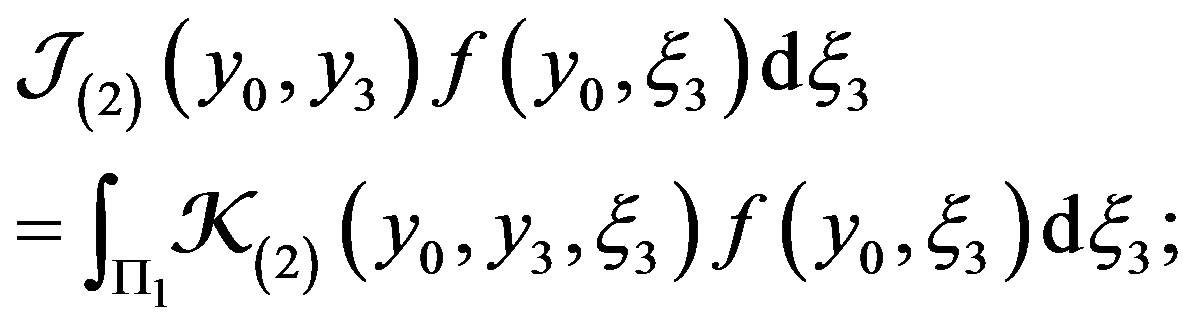
here 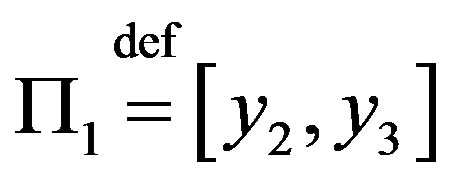 and
and 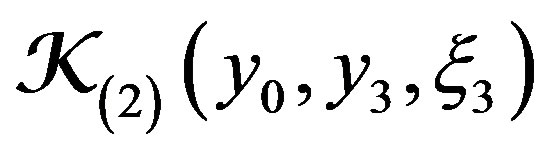 is nonnegative function.
is nonnegative function.
Now recall notation (22); we obtain 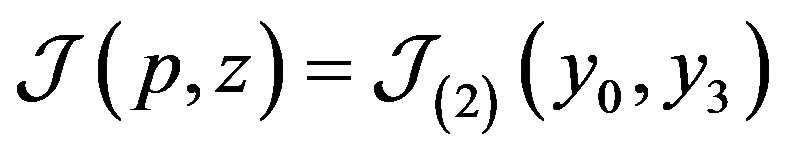 , where
, where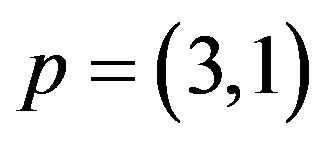 ,
,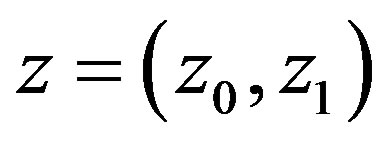 . This completes the proof in discussed case.
. This completes the proof in discussed case.
For an arbitrary natural 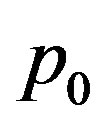 one can obtain a similar representation via multiple integrals with the lower integration limit less than the upper one. Analogously the assertion is proved for
one can obtain a similar representation via multiple integrals with the lower integration limit less than the upper one. Analogously the assertion is proved for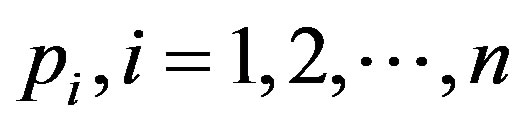 . This completes the proof.
. This completes the proof.
Denote 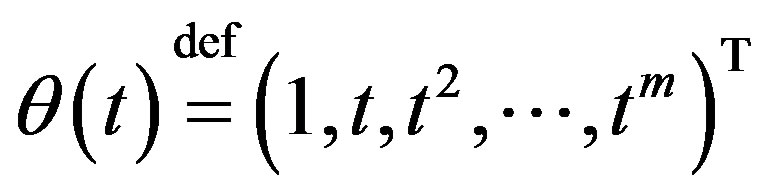 and introduce the function
and introduce the function 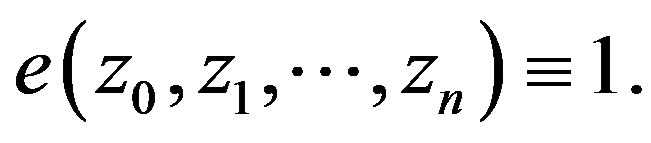
Lemma 2 If suppositions of Lemma 1 are fulfilled, then
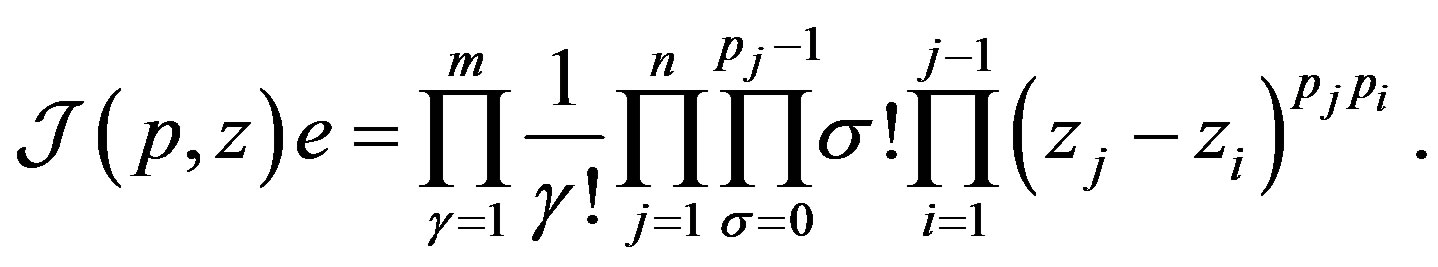 (24)
(24)
Proof Substituting vector-function 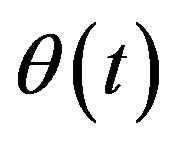 for
for 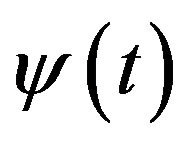 in (13), we have
in (13), we have
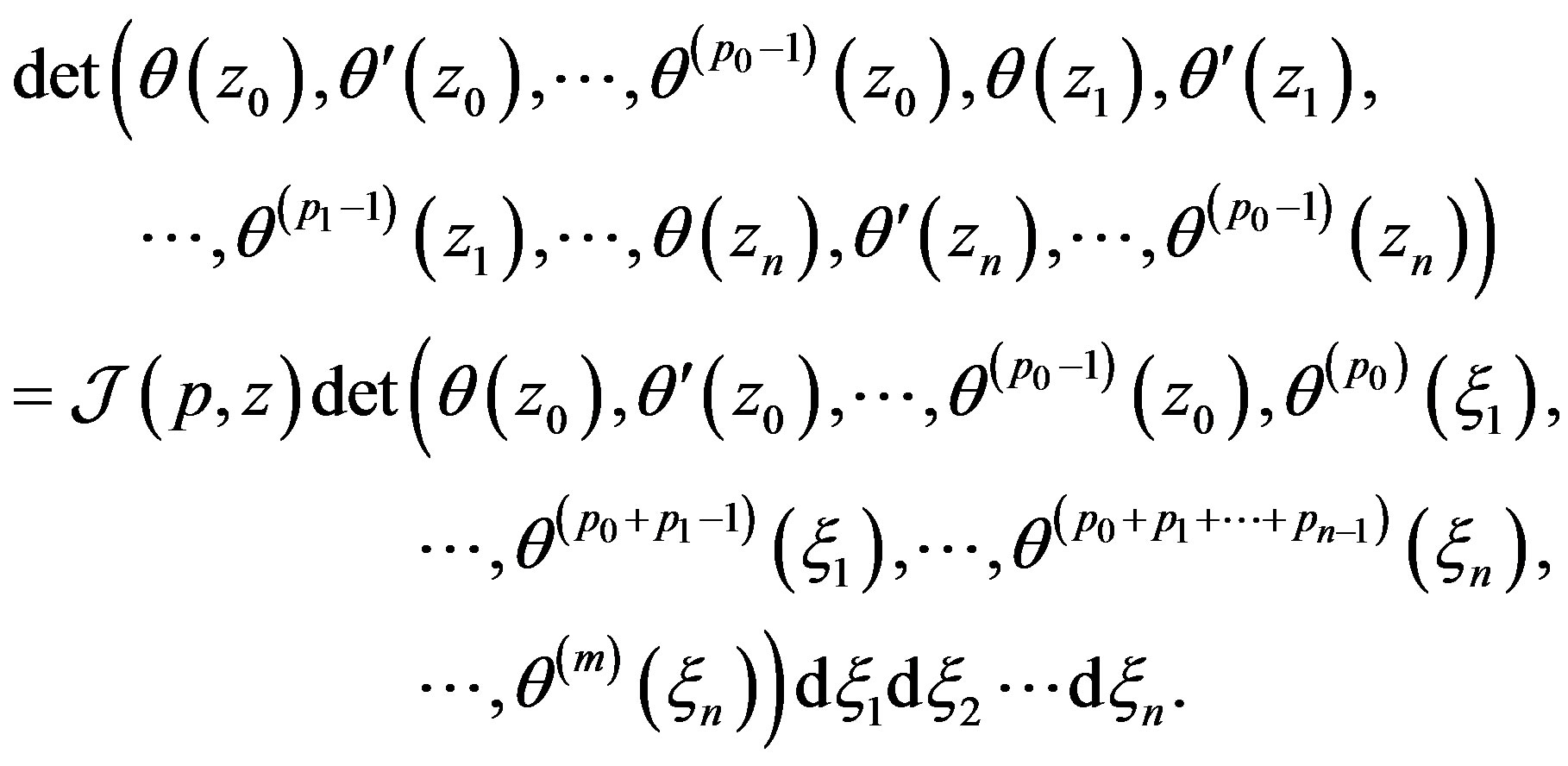 (25)
(25)
The determinant on the right-hand side of (25) contains a lower triangular matrix with entries 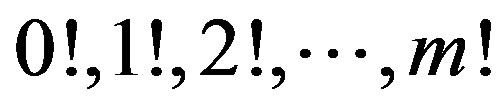 at the main diagonal so that right-hand side is equal to
at the main diagonal so that right-hand side is equal to
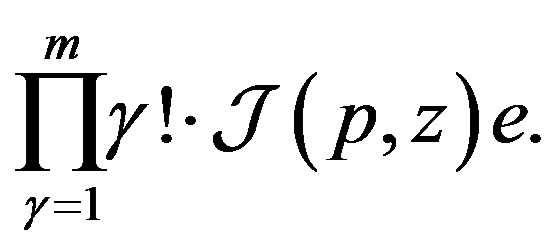 (26)
(26)
The left-hand side contains the determinant of matrix, which appears in Hermite interpolation problem
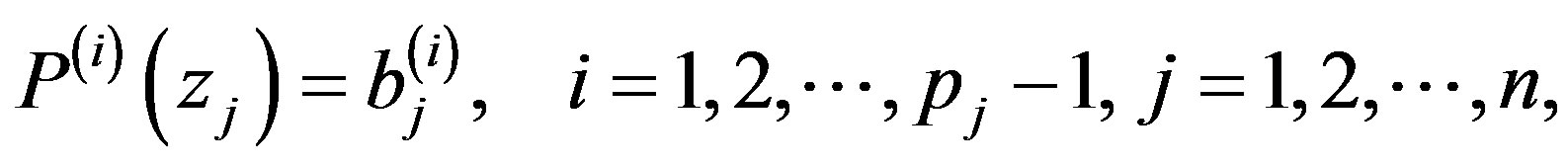
where 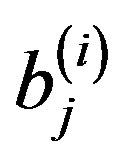 are prescribed numbers and
are prescribed numbers and
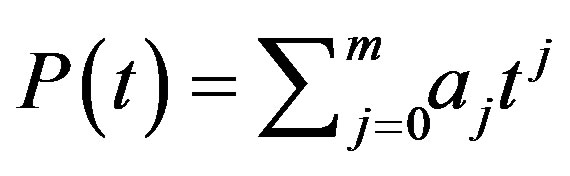 . Value of the mentioned determinant is known (see [3], p. 43); it is equal to
. Value of the mentioned determinant is known (see [3], p. 43); it is equal to
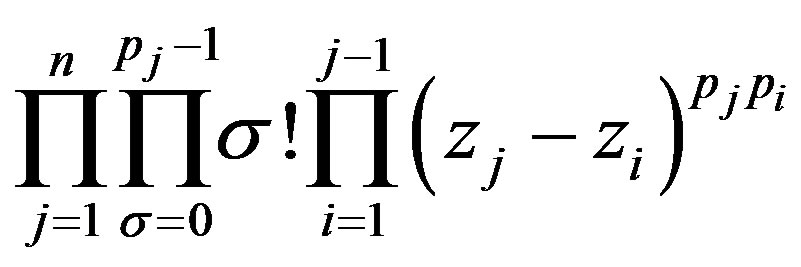 (27)
(27)
Equating of (26) to (27) gives (24). It completes the proof.
4. Evaluations of Approximation by Splines of Hermite Type
We assume that 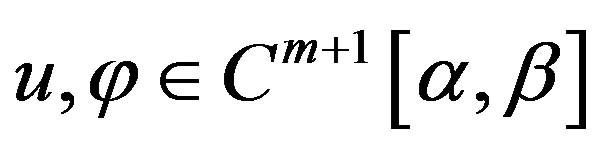 and
and
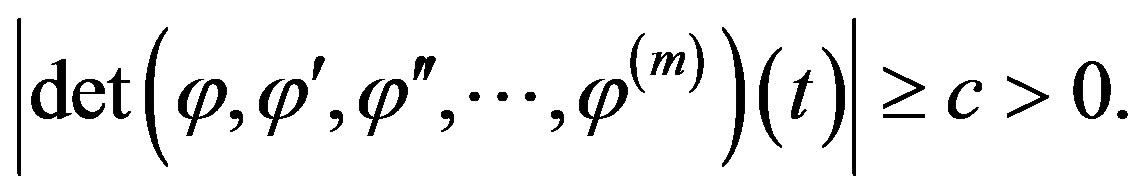 (28)
(28)
By the uniform continuity of the function under consideration on [a,b], from (28) we conclude that for any 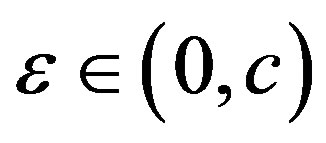 there exists
there exists 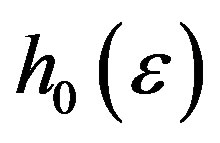 such that for
such that for 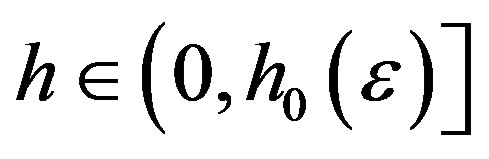 and
and 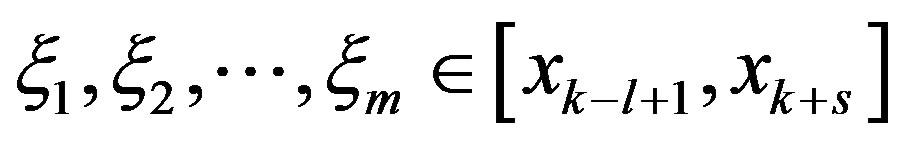
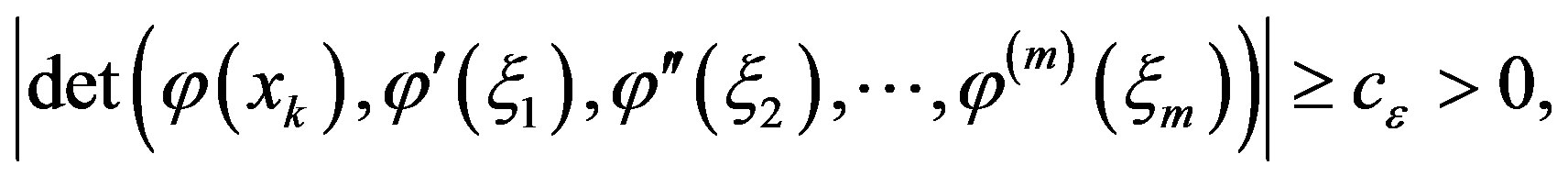 (29)
(29)
where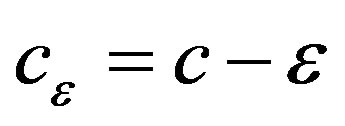 .
.
By definition, put
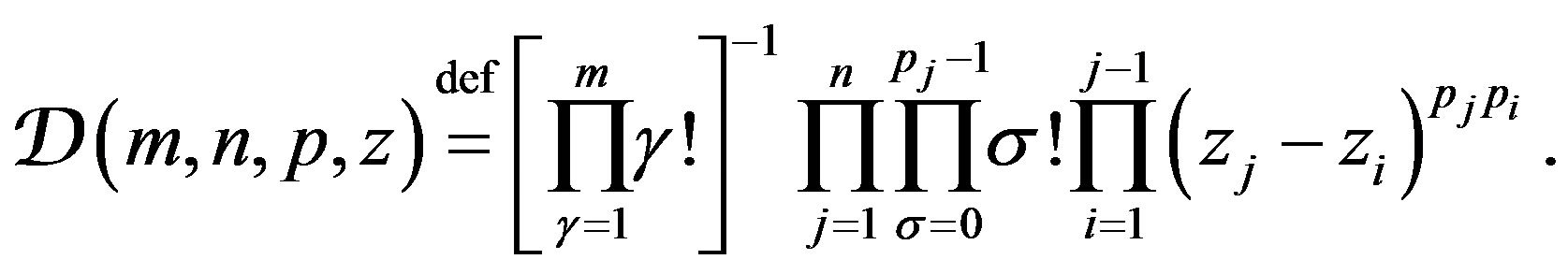
Lemma 3 Under the assumption (29), for 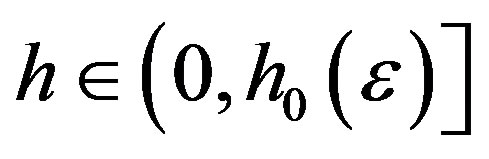 the inequality
the inequality
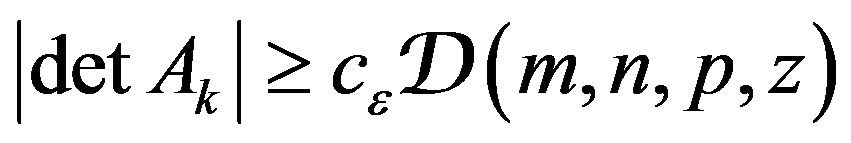 (30)
(30)
is true; here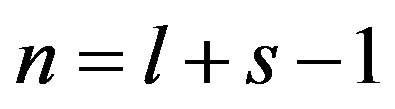 ,
, 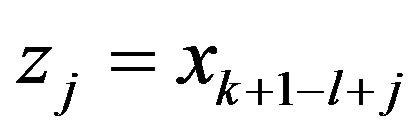 ,
, 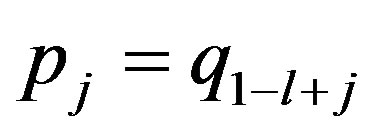 ,
,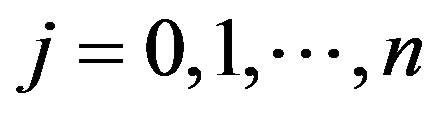 .
.
Proof We use Lemma 1 and represent 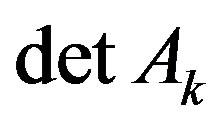 in the form (13) for
in the form (13) for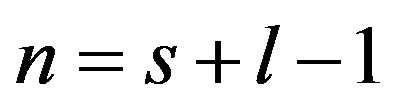 ,
, 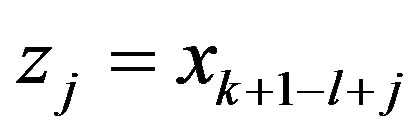 ,
, 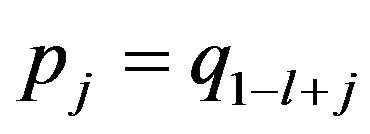 ,
,  ,
,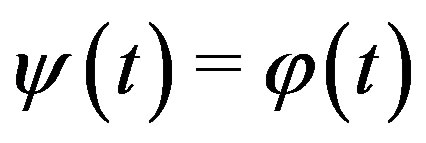 . As a result, we find
. As a result, we find
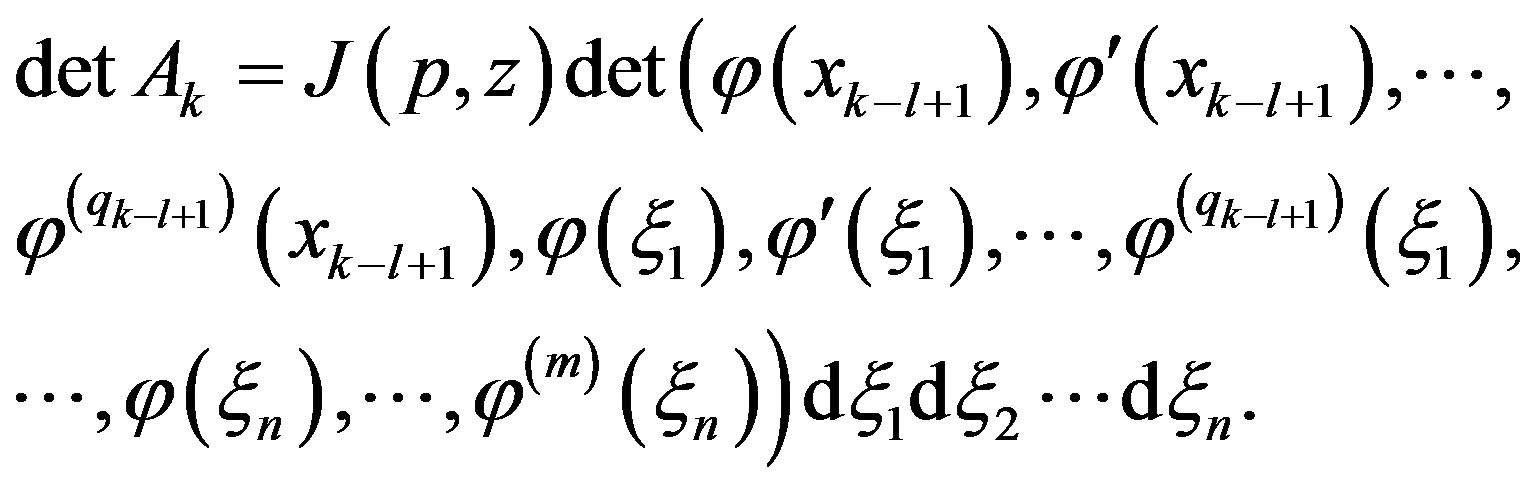
Using the estimate (29), the positiveness of the kernel of the integral operation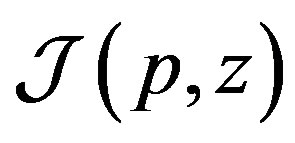 , and the relation (24) obtained in Lemma 2, we derive the estimate (4.3) for
, and the relation (24) obtained in Lemma 2, we derive the estimate (4.3) for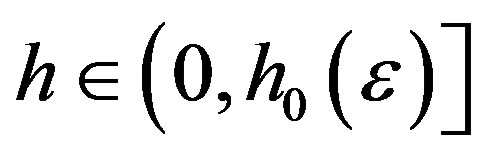 .
.
Now we set
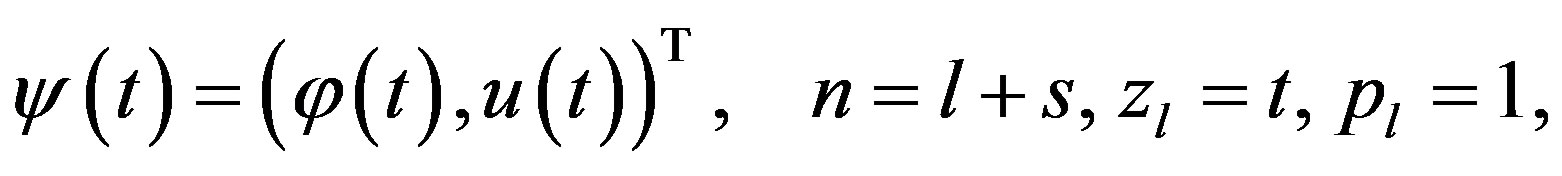 (31)
(31)
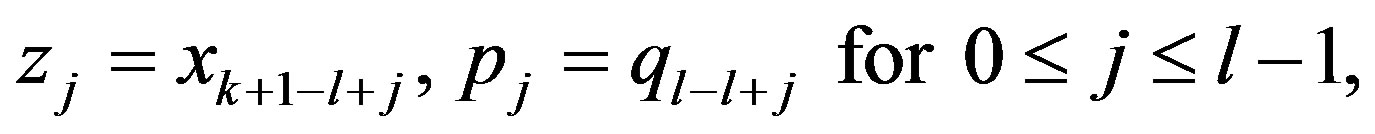 (32)
(32)
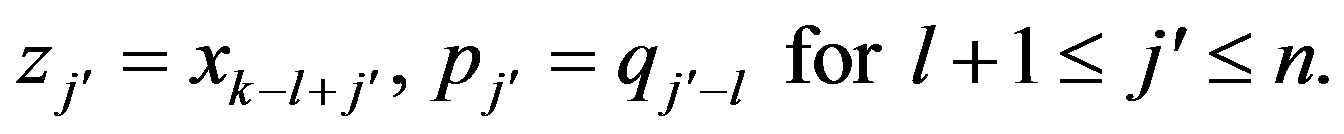 (33)
(33)
Lemma 4 If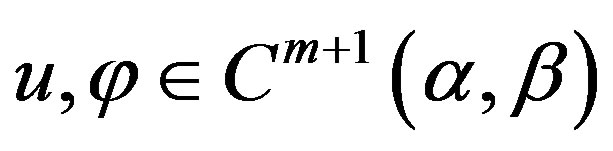 , then for
, then for 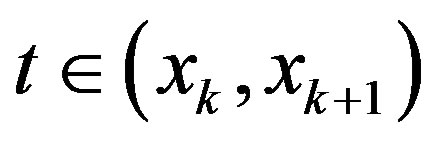 the following inequality holds:
the following inequality holds:
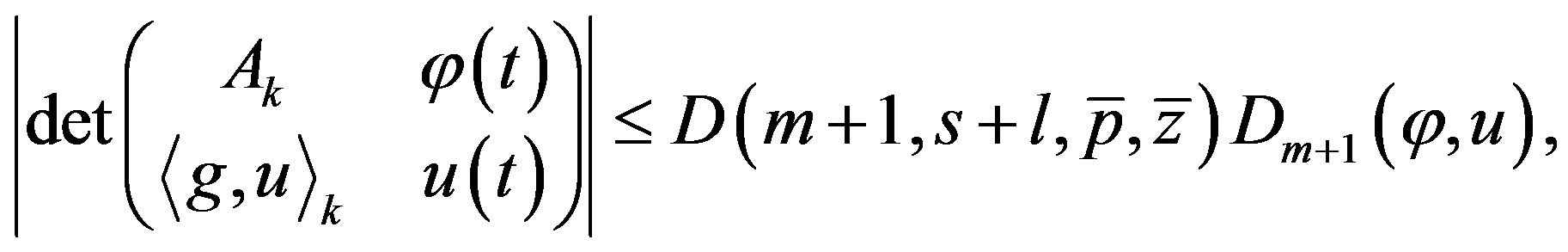 (34)
(34)
where
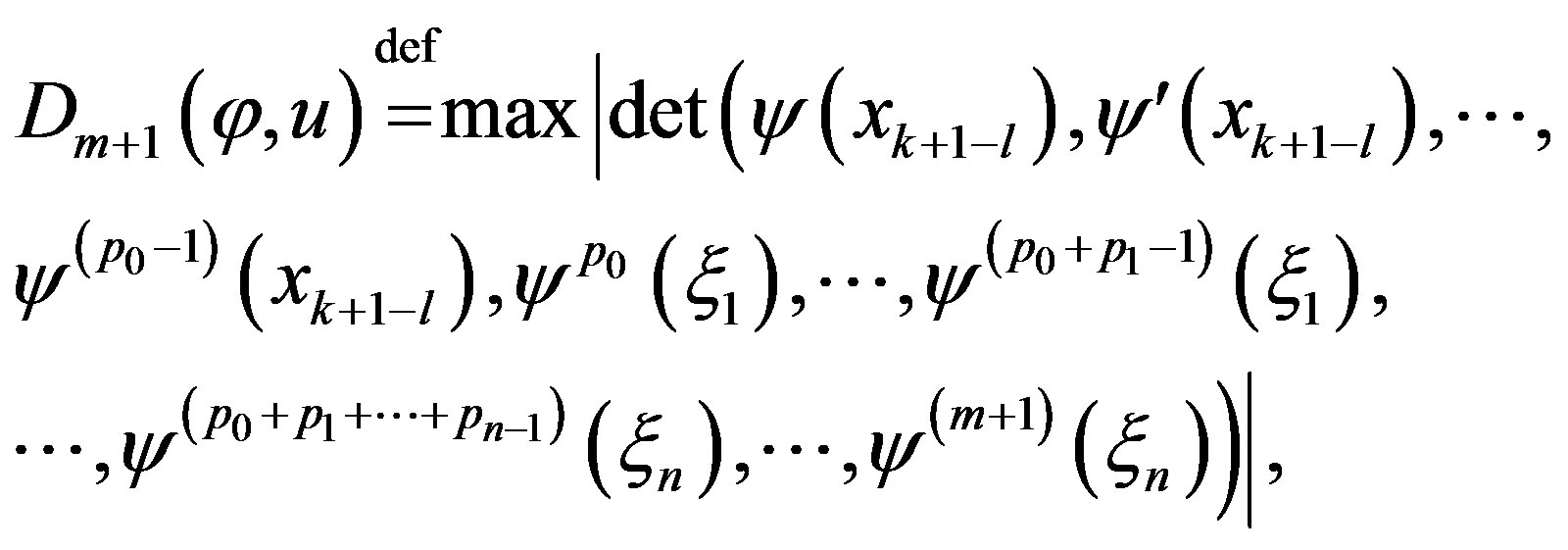 (35)
(35)
and the maximum is taken over
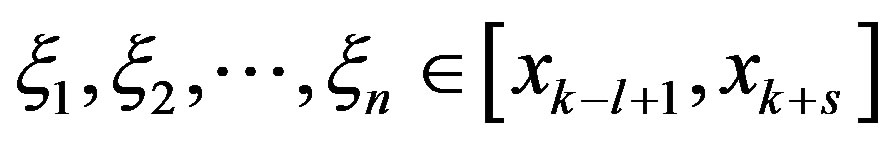
Proof By (31)-(33) the relation (13) may be written in the form
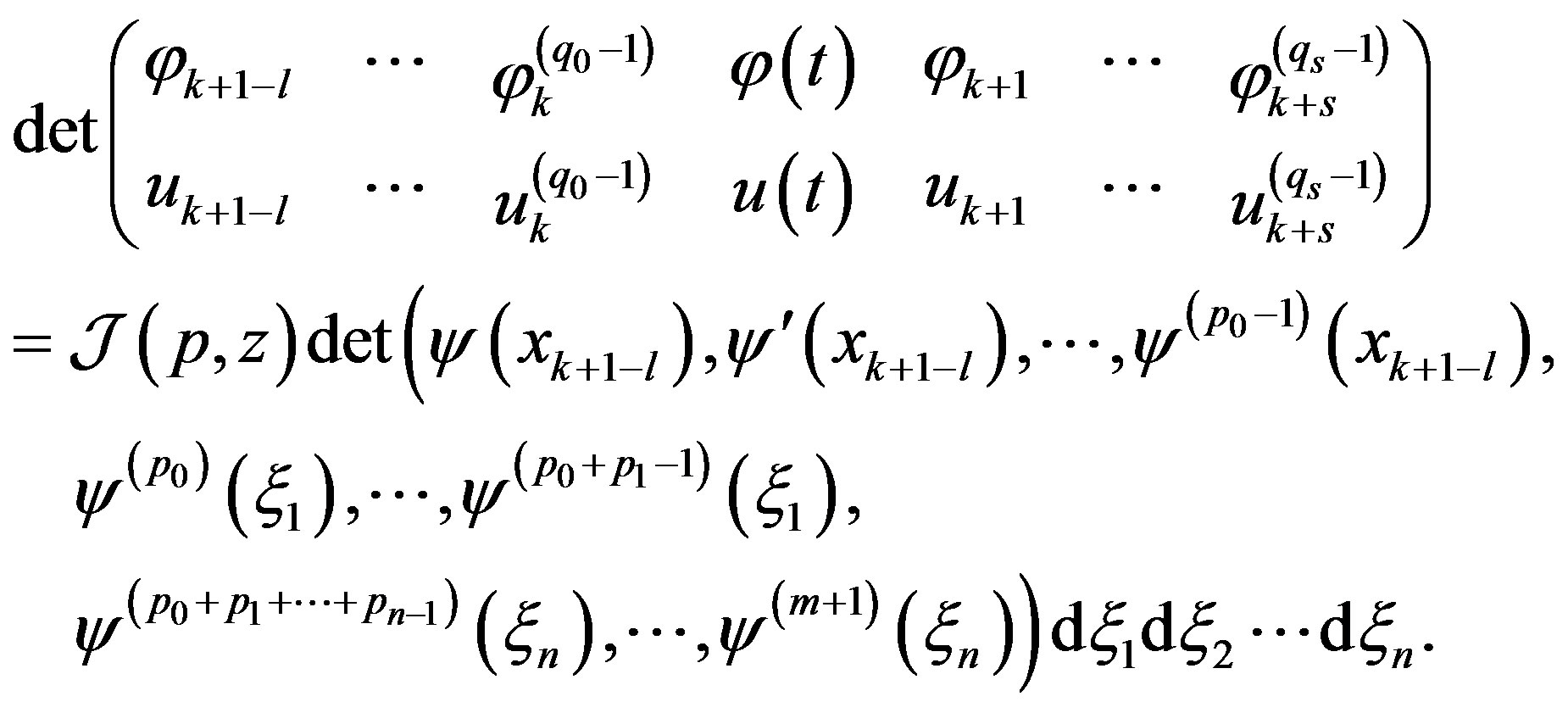
It is clear that conditions of Lemma 1 and Lemma 2 are fulfilled, and therefore the kernel of integral operator 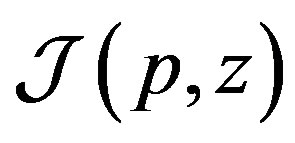 is nonnegative. By Lemma 2 we get evaluation (34)-(35).
is nonnegative. By Lemma 2 we get evaluation (34)-(35).
Theorem 3 If 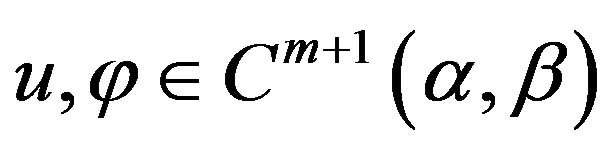 and (29) holds, then for
and (29) holds, then for 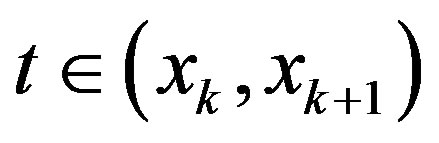
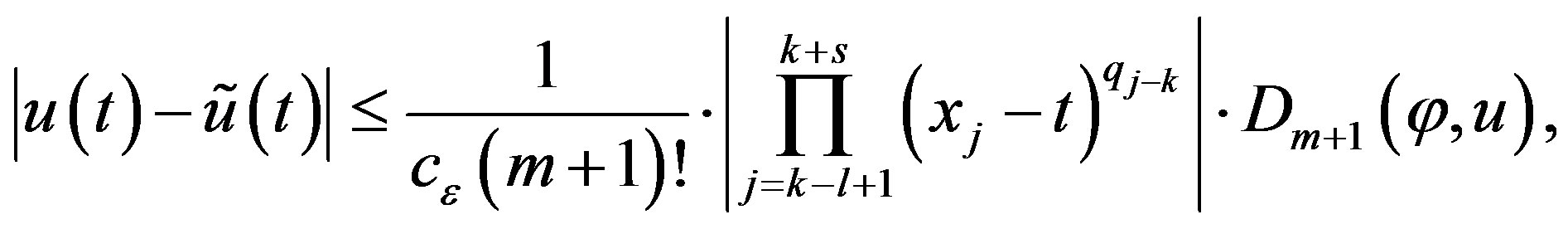 (36)
(36)
where 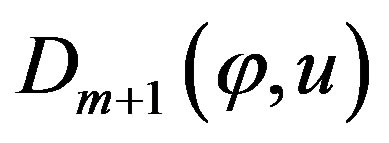 is defined by (35)
is defined by (35)
Proof Usage (34)-(35) in (12) gives the evaluation (36).
Corollary 1 Under the assumptions of Theorem 3, the interpolation 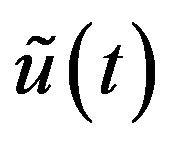 of a function
of a function 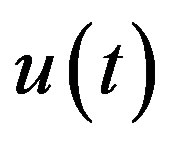 is exact on elements of the space
is exact on elements of the space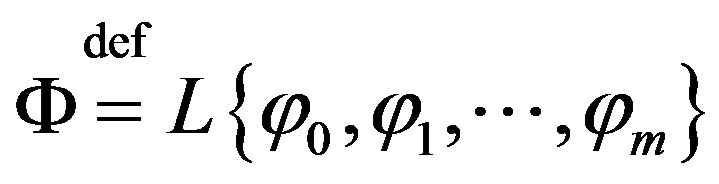 , i.e.,
, i.e.,
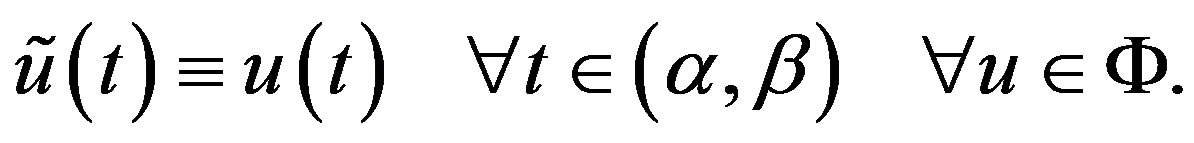 (37)
(37)
Proof If identity 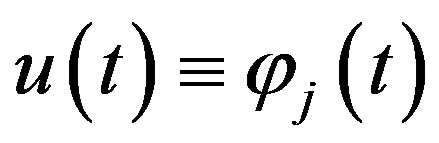 is fulfilled for a number
is fulfilled for a number ,
, 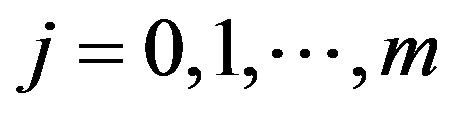 , then in (33) the determinant
, then in (33) the determinant 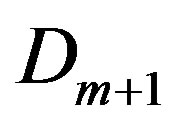 includes two identical rows; therefore
includes two identical rows; therefore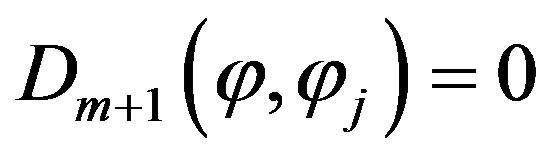 . Thus the relation (37) is true.
. Thus the relation (37) is true.
5. Acknowledgements
The work is partially supported by the Russian Foundation for Basic Research (grant No. 13-01-00096).