Some Properties of a Kind of Singular Integral Operator with Weierstrass Function Kernel ()
1. Introduction
The properties of singular integral operator with Cauchy or Hilbert kernel on simple closed smooth curve or open arc have been elaborately discussed in [1-3]. Based on these, for the boundary curve is a closed curve or an open arc, the authors discussed the singular integral operators and corresponding equation with Cauchy kernel or Hilbert kernel in [1-3]. In recent years, many authors discussed the numerical solution of a class of systems of Cauchy singular integral equations with constant coefficients, Numerical methods for nonlinear singular Volterra integral equations in [4-6].
In this paper, we consider a kind of singular integral operator with Weierstrass function kernel on a simple closed smooth curve in a fundamental period parallelogram. Our goal is to develop the Bertrand poincaré formula for changing order of the corresponding integration, and some important properties of the above singular integral operator.
2. Preliminaries
Definition 1 Suppose that 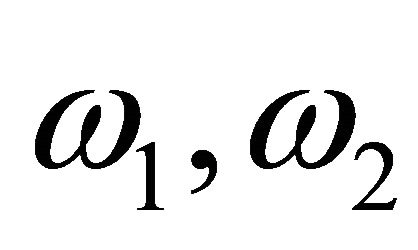 are complex constants with
are complex constants with , and P denotes the fundamental period parallelogram with vertices
, and P denotes the fundamental period parallelogram with vertices . Then the function
. Then the function

is called the Weierstrass  -function, where
-function, where

 denotes the sum of all
denotes the sum of all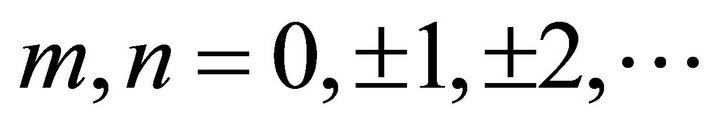 , except for
, except for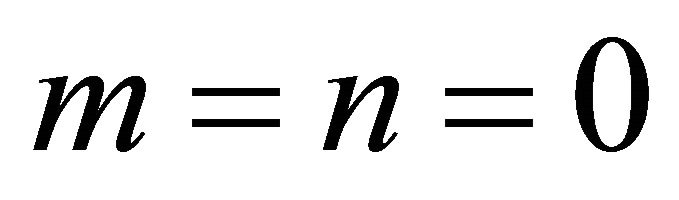 .
.
Definition 2 Suppose that  is a smooth closed curve in the counterclockwise direction, lying entirely in the fundamental period parallelogram P, with
is a smooth closed curve in the counterclockwise direction, lying entirely in the fundamental period parallelogram P, with  and the origin lying in the domain
and the origin lying in the domain 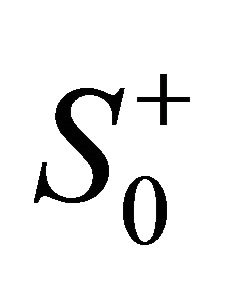 enclosed by
enclosed by . The following operator
. The following operator
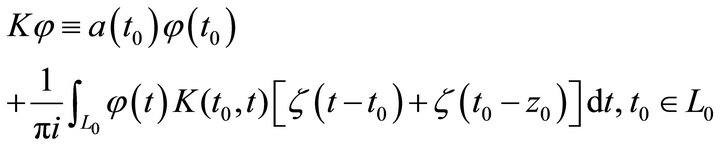 (1)
(1)
is called the singular integral operator with  -function kernel on
-function kernel on , where
, where  is the unknown function, and
is the unknown function, and

are the given functions.
Letting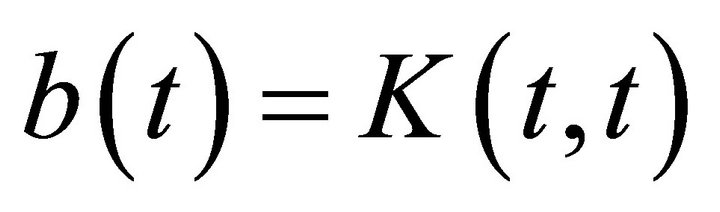 , then (1) becomes
, then (1) becomes
 (2)
(2)
Since  is uniformly convergent in any closed bounded region lying entirely in P,
is uniformly convergent in any closed bounded region lying entirely in P,

for any , where
, where  is some positive finite constant. By noting that
is some positive finite constant. By noting that , we obtain
, we obtain

 , where
, where 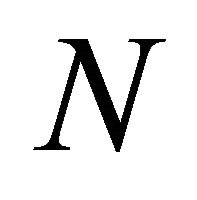 is some positive finite constant. Write
is some positive finite constant. Write


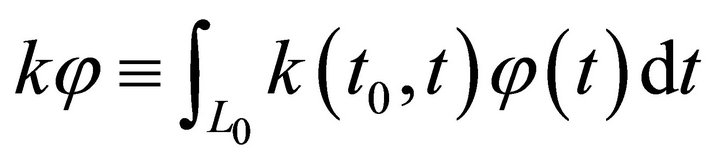
then (1) can be rewritten in the form
 , (3)
, (3)
where 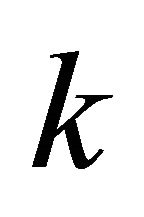 is a Fredholm operator and
is a Fredholm operator and  is called the characteristic operator of
is called the characteristic operator of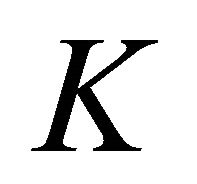 . Now the index of
. Now the index of  is defined as
is defined as , where
, where

and for definiteness we assume that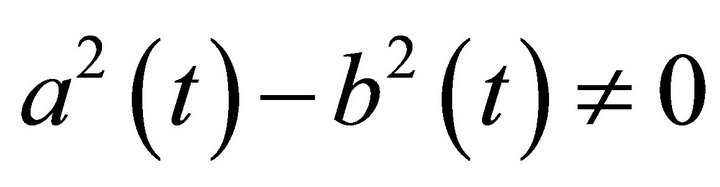 , namely we assume that
, namely we assume that 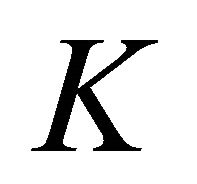 is an operator of normal type.
is an operator of normal type.
Now the associated operator of (1) takes the form
 (4)
(4)
or
 (4)′
(4)′
and so that the associated operator of  becomes
becomes

In addition, if we write

then (4) can be rewritten as
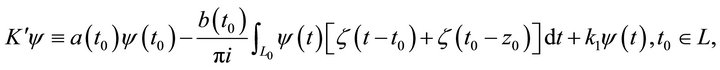 (5)
(5)
where
 (
( ,
, is some finite constant).
is some finite constant).
So  is a Fredholm operator, and then the characteristic operator of
is a Fredholm operator, and then the characteristic operator of  operator becomes
operator becomes
 (6)
(6)
Therefore, we concluded that  usually can not be established, that is
usually can not be established, that is .
.
For convenience, we write
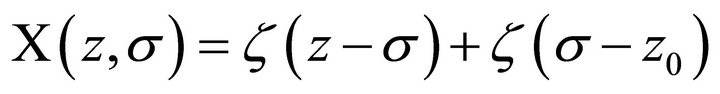
where the fixed nonzero point  and the origin lie in
and the origin lie in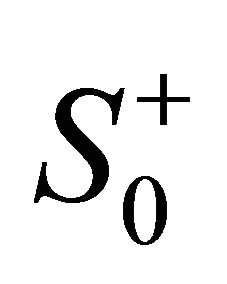 . It is not difficult to get the following results.
. It is not difficult to get the following results.
Lemma 1 Suppose that , and with the same
, and with the same  as mentioned before, then a)
as mentioned before, then a) 
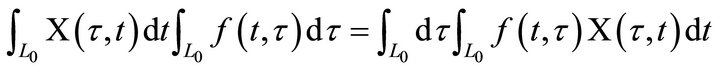
b) (Poincare-Bertrand formula)
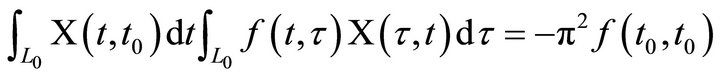
3. Some Properties of Operator K
1) If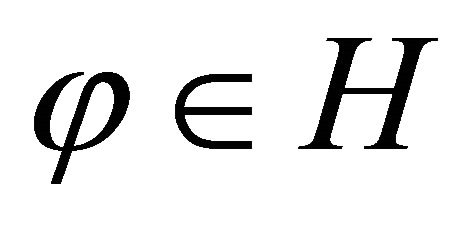 , then
, then .
.
Proof Through calculation and estimation, we have
 (7)
(7)
for any , where
, where  and
and  are all finite constant. While for any
are all finite constant. While for any , we have
, we have
 (8)
(8)
where  is some finite constant. Substituting (8) into (7), we obtain
is some finite constant. Substituting (8) into (7), we obtain
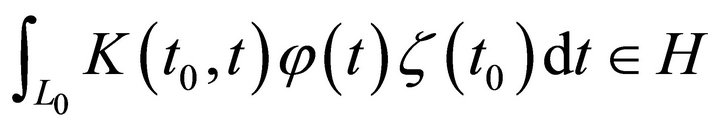 (9)
(9)
Similarly we know that

Consequently, we have .
.
2) If  are singular integral operator, then
are singular integral operator, then  is also a singular integral operator. That is, if
is also a singular integral operator. That is, if

then
 , (10)
, (10)
where the sum of the former two terms in the right hand of Equation (10) are the characteristic operator, and the remainder in that is a Fredholm operator.
Proof By definition, we deduce that

where
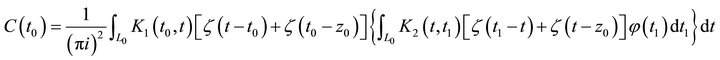
By virtue of Lemma 1 (b),  can be rewritten in the form
can be rewritten in the form

Consequently, (10) is established.
Now we write

where
 ,
,  ,
,
 ,
,
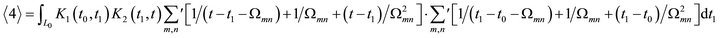 .
.
By [1], we know that  is a Fredholm integral. For
is a Fredholm integral. For , we know from
, we know from
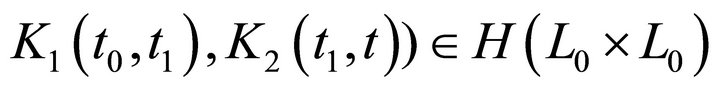
that  is continuous about the variable
is continuous about the variable , and so that
, and so that  is also a Fredholm integral. By nothing that
is also a Fredholm integral. By nothing that  have the same form, we only need to discuss either one of them. Here we consider the integral
have the same form, we only need to discuss either one of them. Here we consider the integral . Write
. Write

then  is analytic in P and so that
is analytic in P and so that . Consequently, we read from
. Consequently, we read from

that  and so that
and so that  is continuous on
is continuous on , therefore
, therefore  is also a Fredholm integral.
is also a Fredholm integral.
So far, we conclude that  is a singular integral operator.
is a singular integral operator.
3) Let , where
, where  denotes the indices of
denotes the indices of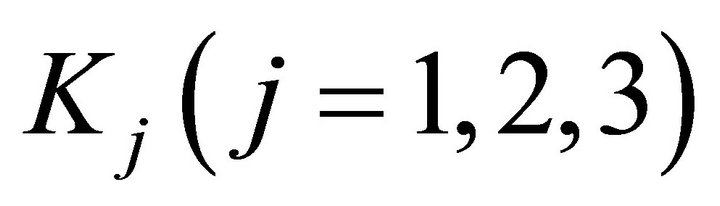 , then
, then .
.
Proof From 2), we know
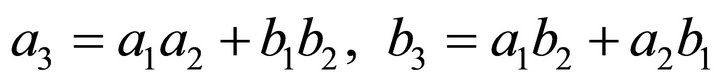
and

so .
.
In addition, we can see from
 and
and that when
that when  are normal,
are normal,  is also normal.
is also normal.
4)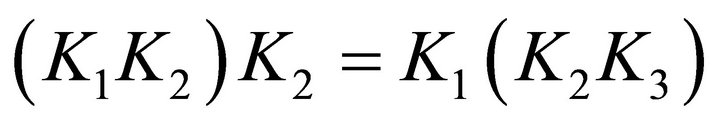 .
.
5) If  is a singular integral operator, and
is a singular integral operator, and  is a Fredholm integral operator of the first kind, then
is a Fredholm integral operator of the first kind, then  and
and  are also Fredholm integral operators of the first kind.
are also Fredholm integral operators of the first kind.
6) If the indies of  and
and  are
are  and
and  respectively , then
respectively , then .
.
7) .
.
Through careful calculation, we may obtain 4) - 7).
8) Generally speaking,

can not be established for .
.
Proof By definition and calculation, we have
 . (11)
. (11)
Whereas
 . (12)
. (12)
Let

then by Lemma 1(a), we have
 , (13)
, (13)
Substituting (13) into (12), we see that
 . (14)
. (14)
Therefore,  cannot be established.
cannot be established.