Existence and Uniqueness of Solutions to Impulsive Fractional Integro-Differential Equations with Nonlocal Conditions ()
1. Introduction
Fractional differential equations appear naturally in a number of fields such as physics, engineering, biophysics, blood flow phenomena, aerodynamics, electron-analytical chemistry, biology, control theory, etc., An excellent account in the study of fractional differential equations can be found in [1-11] and references therein. Undergoing abrupt changes at certain moment of times like earthquake, harvesting, shock etc, these perturbations can be well-approximated as instantaneous change of state or impulses. Furthermore, these processes are modeled by impulsive differential equations. In 1960, Milman and Myshkis introduced impulsive differential equations in their papers [12]. Based on their work, several monographs have been published by many authors like Semoilenko and Perestyuk [13], Lak-shmikantham et al. [14], Bainov and Semoinov [15,16], Bainov and Covachev [17] and Benchohra et al. [18]. Impulsive fractional differential equations represent a real framework for mathematical modelling to real world problems. Significant progress has been made in the theory of impulsive fractional differential equations [19-21].
We consider a class of impulsive fractional integrodifferential equations with nonlocal conditions of the form
 (1.1)
(1.1)
 (1.2)
(1.2)
 (1.3)
(1.3)
Where  is the Caputo fractional derivative, the function
is the Caputo fractional derivative, the function 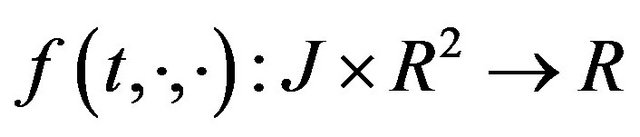 is continuous and the function
is continuous and the function 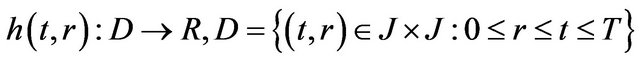 is continuous,
is continuous, 

and  represent the right and left limits of
represent the right and left limits of 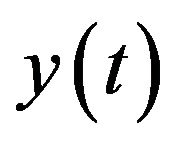 at
at , and
, and is a continuous function,
is a continuous function, .
.
Nonlocal conditions were initiated by Byszewski [22] who proved the existence and uniqueness of mild and classical solutions of nonlocal Cauchy problems. As remarked by Byszewski [23,24], the nonlocal condition can be more useful than the standard initial condition to describe some physical phenomena. For example,  may be given by
may be given by
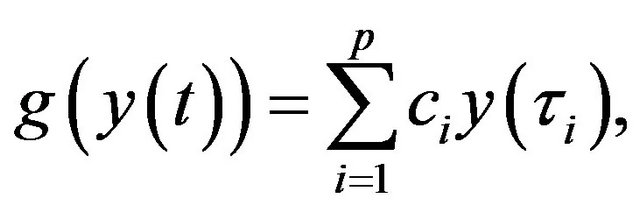
where  are given constants and
are given constants and 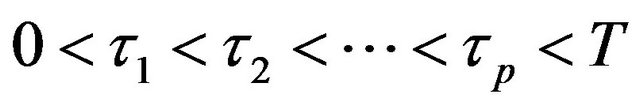 .
.
In this article, our aim is to show sufficient conditions for the existence and uniqueness of solutions of solutions to impulsive fractional integro-differential equations with nonlocal conditions.
2. Preliminaries
In this section, we introduce some notations, definitions and preliminary facts which are used throughout this paper. By  we denote the Banach space of all continuous functions from
we denote the Banach space of all continuous functions from  into
into  with the norm
with the norm
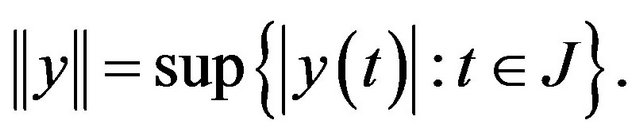
Definition 2.1 [5,8]: The fractional (arbitrary) order integral of the function  of order
of order  is defined by
is defined by

where  is the gamma function, when
is the gamma function, when 
Definition 2.2 [5,8]: For a function  given on the interval
given on the interval , Riemann-Liouville fractional-order derivative of order
, Riemann-Liouville fractional-order derivative of order  of
of , is defined by
, is defined by

here 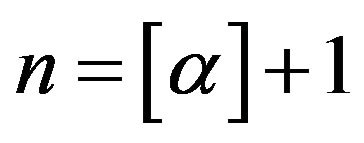 and
and  denotes the integer part of
denotes the integer part of
 , when
, when .
.
Definition 2.3 [14]: For a function  given on the interval
given on the interval , the Caputo fractional-order derivative of order
, the Caputo fractional-order derivative of order 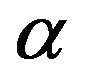 of
of , is defined by
, is defined by

where .
.
Lemma 2.4 [25]: (Schaefer’s fixed point theorem). Let  be a Banach space and
be a Banach space and  be a completely continuous operator. If the set
be a completely continuous operator. If the set
 is bounded, then
is bounded, then 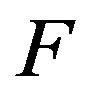 has at least a fixed point in X.
has at least a fixed point in X.
3. Existence of Solutions
Consider the set of functions

Definition 3.1: A function 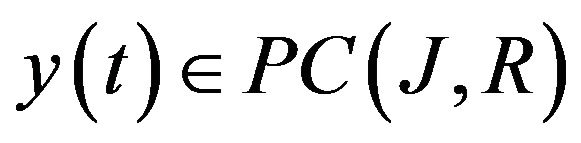 whose
whose  -derivative exists on
-derivative exists on  is said to be a solution of (1.1)-(1.3), if
is said to be a solution of (1.1)-(1.3), if  satisfies the equation
satisfies the equation

on 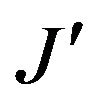 and satisfies the conditions
and satisfies the conditions

where .
.
To prove the existence of solutions to (1.1)-(1.3), we need the following auxiliary lemmas.
Lemma 3.2: Let , then the equation
, then the equation

has solutions

Lemma 3.3: Let , then
, then

for some .
.
As a consequence of Lemma 3.2 and Lemma 3.3, we have the following result Lemma 3.4: Let , and let
, and let  be continuous. A function
be continuous. A function 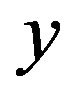 is a solution of the fractional integral equation
is a solution of the fractional integral equation
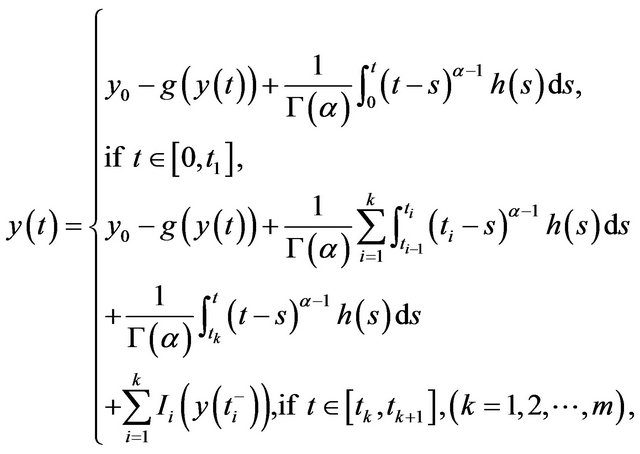 (3.1)
(3.1)
if and only if  is a solution of the fractional nonlocal BVP
is a solution of the fractional nonlocal BVP
 (3.2)
(3.2)
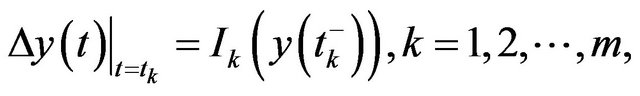 (3.3)
(3.3)
 (3.4)
(3.4)
Proof Assume 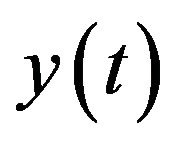 satisfies (3.2)-(3.4).
satisfies (3.2)-(3.4).
If 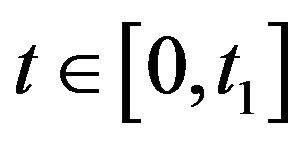 then
then .
.
Lemma 3.3 implies
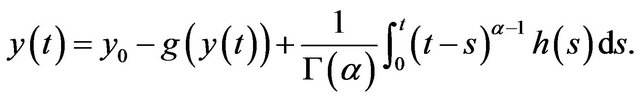
If , by Lemma 3.3, it follows that
, by Lemma 3.3, it follows that

If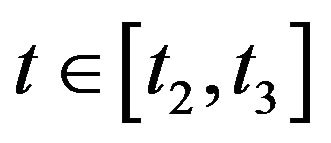 , then from Lemma 3.3 we get
, then from Lemma 3.3 we get
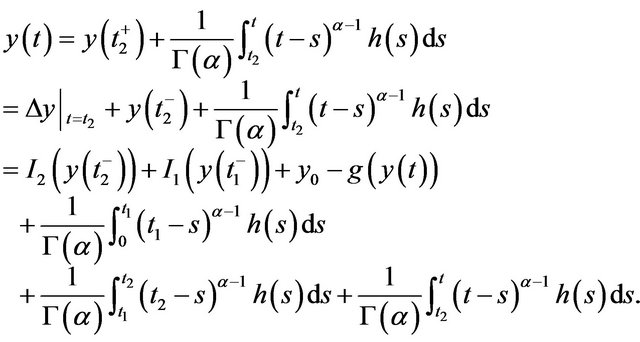
If , then again from
, then again from 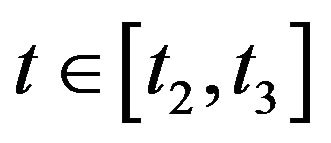 we have (3.1).
we have (3.1).
Conversely, assume that  satisfies the impulsive fractional integral equation (3.1). If
satisfies the impulsive fractional integral equation (3.1). If , then
, then  and using the fact that
and using the fact that  is the left inverse of
is the left inverse of , we get
, we get .
.
If  and using the fact that
and using the fact that , where
, where  is a constant, we conclude that
is a constant, we conclude that 
Also, we can easily show that

Theorem: Assume that:
(H1) There exists a constant  such that
such that
 for each
for each  and each
and each ;
;
(H2) There exists a constant 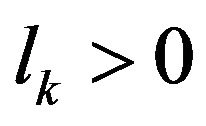 such that
such that
 , for each
, for each  and
and ;
;
(H3) There exists a constant  such that
such that
 , for each
, for each , then the problem
, then the problem
(1.1)-(1.3) has at least one solution on .
.
Proof Consider the operator
 defined by
defined by

Clearly, the fixed points of the operator  are solution of the problem (1.1)-(1.3).
are solution of the problem (1.1)-(1.3).
We shall use Schaefer’s fixed point theorem to prove that 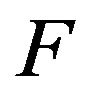 has a fixed point. The proof will be given in several steps.
has a fixed point. The proof will be given in several steps.
Step 1:  is continuous.
is continuous.
Let  be a sequence such that
be a sequence such that  in
in . Then for each
. Then for each
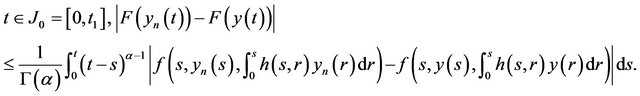
Since  is continuous function, we have
is continuous function, we have
 as
as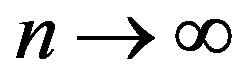 .
.
For each ,
,

Since  and
and  are continuous functions, we have
are continuous functions, we have  as
as .
.
Therefore,  is continuous.
is continuous.
Step 2: 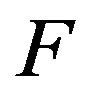 maps bounded sets into bounded sets in
maps bounded sets into bounded sets in .
.
Indeed, it is enough to show that for any , there exists a positive constant
, there exists a positive constant  such that for each
such that for each
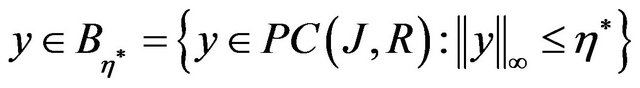 , we have
, we have
 . By (H1), (H2) and (H3), for each
. By (H1), (H2) and (H3), for each , we have
, we have
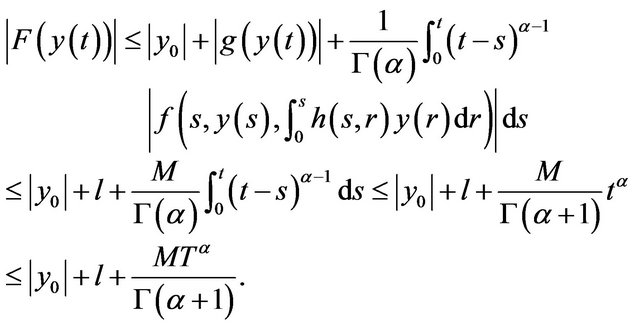
For , we have
, we have

Let
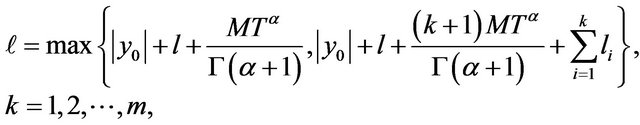
then 
Step 3:  maps bounded sets into equicontinuous sets of
maps bounded sets into equicontinuous sets of .
.
Let ,
, 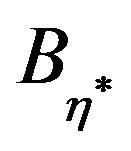 be a bounded set of
be a bounded set of  as in Step 2, and let
as in Step 2, and let . For
. For
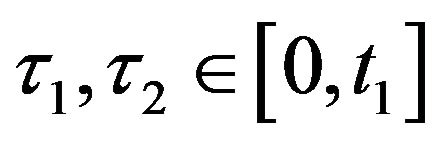 , we have
, we have

For , we have
, we have

As , the right-hand side of the above inequality tends to zero. As a consequence of Steps 1 to 3 together with the Arzel’a-Ascoli theorem, we can conclude that
, the right-hand side of the above inequality tends to zero. As a consequence of Steps 1 to 3 together with the Arzel’a-Ascoli theorem, we can conclude that  is completely continuous.
is completely continuous.
As a consequence of Lemma 2.4 (Schaefer’s fixed point theorem), we deduce that  has a fixed point which is a solution of the problem (1.1)-(1.3).
has a fixed point which is a solution of the problem (1.1)-(1.3).
4. Acknowledgements
This work was supported by the natural science foundation of Hunan Province (13JJ6068, 12JJ9001), Hunan provincial science and technology department of science and tech-neology project (2012SK3117), Science foundation of Hengyang normal university of China (No. 12B35) and Construct program of the key discipline in Hunan Province.