Positive-Definite Operator-Valued Kernels and Integral Representations ()
1. Introduction
About the scalar complex trigonometric moment problem we recall that: a sequence  of complex numbers with
of complex numbers with  is called positive semi-definite if for each
is called positive semi-definite if for each
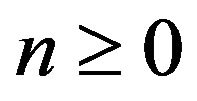 , the Toeplitz matrix
, the Toeplitz matrix  is positive semi-definite. The problem of characterising the positive semi-definiteness of a sequence of complex numbers was completely solved by Carathéodory in [1], in the following theorem:
is positive semi-definite. The problem of characterising the positive semi-definiteness of a sequence of complex numbers was completely solved by Carathéodory in [1], in the following theorem:
Theorem 1. The Toeplitz matrix 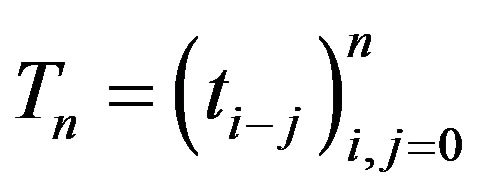 is positive semi-definite and rank
is positive semi-definite and rank  with
with  if and only if the matrix
if and only if the matrix  is invertible and there exists
is invertible and there exists 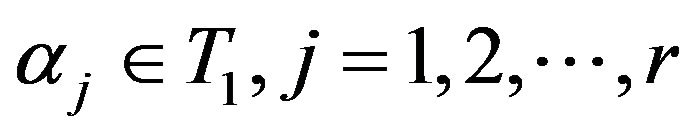 with
with 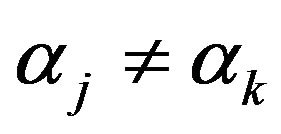 for
for  and
and

such that
 (1.1)
(1.1)
In the same paper [1], Charathéodory also proved that: if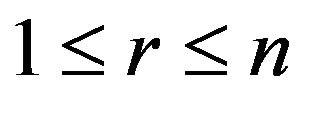 , then
, then  are the roots of the polynomial
are the roots of the polynomial
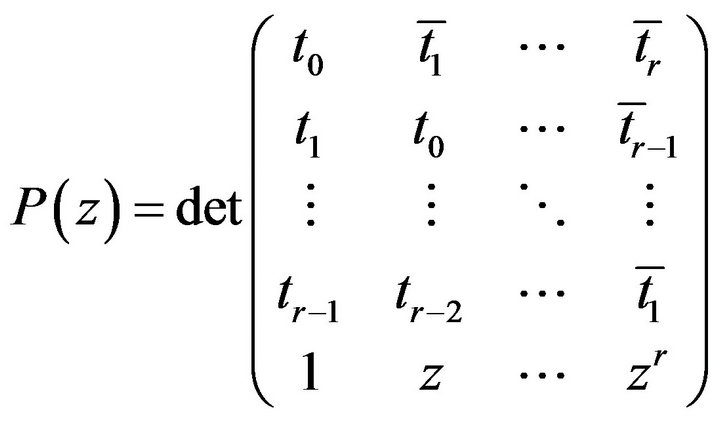
which are all distinct and belong to 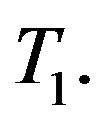
Another characterization of the positive semi-definiteness of a sequence of complex numbers was obtained by Herglotz in [2]. In [2], for , the
, the  moment of a finite measure
moment of a finite measure  on
on  is defined by
is defined by

The following characterization of the positivity of a complex moment sequence is the main result in [2].
Theorem 2. A sequence of complex numbers ,
,  is positive semi-definite if and only if there exists a positive measure
is positive semi-definite if and only if there exists a positive measure  on the unit circle
on the unit circle  such that
such that 
From Theorem 1 and Theorem 2, Charathéodory and Fejér in [3] deduce the following theorem:
Theorem 3. Let  be given complex numbers.
be given complex numbers.
Then there exists a positive measure  on
on  such that
such that
 (1.2)
(1.2)
if and only if the Toeplitz matrix  is positive semi-definite. Moreover, if
is positive semi-definite. Moreover, if 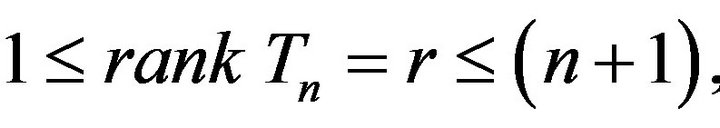 then there exists a positive measure
then there exists a positive measure  supported on
supported on  points of the unit circle
points of the unit circle  which satisfies (1.2.)
which satisfies (1.2.)
Theorem 3 gives an answer to the scalar, truncated trigonometric moment problem.
Operator-valued truncated moment problems were studied in [4,5]. Regarding the truncated, trigonometric operator-valued moment problem, we recall that:
1) ,
,  is called a spectral function if
is called a spectral function if  each
each  is a bounded, positive operator,
is a bounded, positive operator,
 ; it is orthogonal if each
; it is orthogonal if each 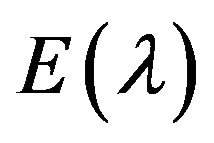 is an othogonal projection;
is an othogonal projection;
2) a finite sequence  of bounded operators on an arbitrary Hilbert space is called a trigonometric moment sequence if, there exists a spectral function
of bounded operators on an arbitrary Hilbert space is called a trigonometric moment sequence if, there exists a spectral function 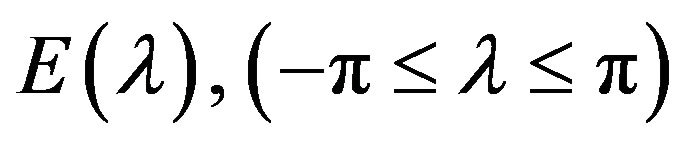 such that
such that 
for every  In [4], the necessary and sufficient condition of representing a finite sequence of bounded operators on an arbitrary Hilbert space H,
In [4], the necessary and sufficient condition of representing a finite sequence of bounded operators on an arbitrary Hilbert space H,  with
with  as a trigonometric moment sequence is the positivity of the Toeplitz matrix
as a trigonometric moment sequence is the positivity of the Toeplitz matrix
 obtained with the given operators. The representing spectral function is obtained in [4] by generating an unitary operator, defined on the direct sum of
obtained with the given operators. The representing spectral function is obtained in [4] by generating an unitary operator, defined on the direct sum of  copies of the Hilbert space H for obtaining an orthogonal spectral function and by applying Naimark’s dilation theorem to get the representing spectral function from it. In [5], a multidimensional operator-valued truncated moment problem is solved. That is: given a sequence of bounded operators
copies of the Hilbert space H for obtaining an orthogonal spectral function and by applying Naimark’s dilation theorem to get the representing spectral function from it. In [5], a multidimensional operator-valued truncated moment problem is solved. That is: given a sequence of bounded operators
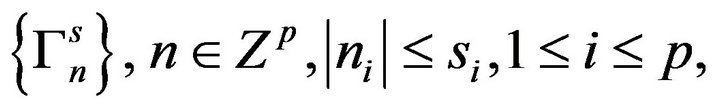
acting on an arbitrary Hilbert space H, with

a necessary and sufficient condition for representing any such operator
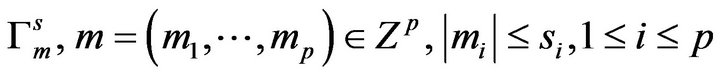
as the 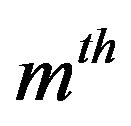 moment of a positive operator-valued measure is given. The necessary and sufficient condition in [5] for such a representation is again the positivity of the Toeplitz matrix
moment of a positive operator-valued measure is given. The necessary and sufficient condition in [5] for such a representation is again the positivity of the Toeplitz matrix

obtained with the given operators. The representing positive operator-valued measure, (spectral function), in [5] is obtained by applying Kolmogorov’s decomposition positive kernels theorem.
Concerning the complex, operator-valued moment problem on a compact semialgebraic nonvoid set , we recall that a sequence of bounded operators
, we recall that a sequence of bounded operators
 acting on an arbitrary complex Hilbert spacea H, subject on the conditions
acting on an arbitrary complex Hilbert spacea H, subject on the conditions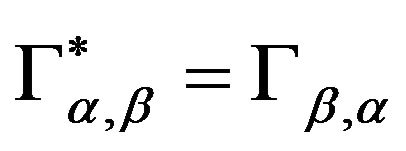 ,
,  is called a
is called a  moment sequence if there exists an operator-valued positive measure
moment sequence if there exists an operator-valued positive measure 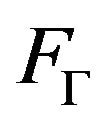 on
on 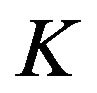 such that
such that
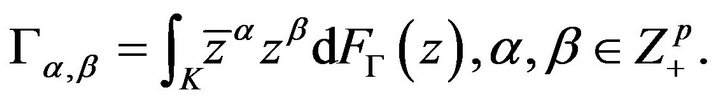
A sequence of bounded operators  with
with  and
and , acting on an arbitrary, complex, Hilbert space is called a trigonometric operator-valued moment sequence, if there exists a positive, operator-valued measure
, acting on an arbitrary, complex, Hilbert space is called a trigonometric operator-valued moment sequence, if there exists a positive, operator-valued measure 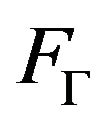 on the p-dimensional complex torus
on the p-dimensional complex torus  such that
such that  for all
for all
 Some of the papers devoted to operator-valued moment problems are: [6-10], to quote only few of them. The operator-valued multidimensional complex moment problem is solved in [9] in the class of commuting multioperators that admit normal extension (subnormal operators) (Theorem 1.4.8., p. 188). In [9], Corollary 1.4.10., a necessary and sufficient condition for solving a trigonometric operator-valued moment problem is given. In [10], another proof of a quite similar necessary and sufficient existence condition on a sequence of bounded operators to admit an integral representation as trigonometric moment sequence with respect to some positive operator valued measure is given. In Section 4 of this note, we prove that the two existence conditions in [9,10] are equivalent.
Some of the papers devoted to operator-valued moment problems are: [6-10], to quote only few of them. The operator-valued multidimensional complex moment problem is solved in [9] in the class of commuting multioperators that admit normal extension (subnormal operators) (Theorem 1.4.8., p. 188). In [9], Corollary 1.4.10., a necessary and sufficient condition for solving a trigonometric operator-valued moment problem is given. In [10], another proof of a quite similar necessary and sufficient existence condition on a sequence of bounded operators to admit an integral representation as trigonometric moment sequence with respect to some positive operator valued measure is given. In Section 4 of this note, we prove that the two existence conditions in [9,10] are equivalent.
The present note studies in Section 3 the representation measure of the truncated operator-valued moment problem in [5], only when the given operators act on a finite dimensional Hilbert space. In Proposition 3.1, Section 3, it is shown that the representing measure, in this case, is an atomic one. In Proposition 3.2, Section 3, the necessary and sufficient existence condition in Proposition 3.1 is stated also in terms of matrices.
In Section 4 of the note, is studied the connection between the problem of representing the terms of an operator sequence

as moments of an operator valued, positive measure and the problem of Riesz-Herglotz type integral representation of some operator-valued, analytic function, with positive real part in the class of operators.
2. Preliminaries
Let  arbitrary,
arbitrary,



denote the complex, respectively the real variable in the complex, respectively real euclidian space. For
 we denote
we denote

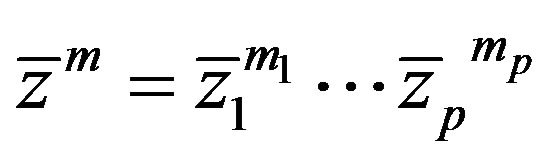
and by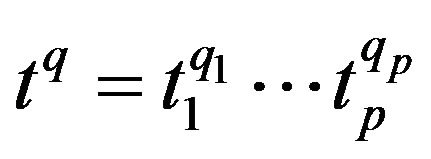 . The sets:
. The sets:
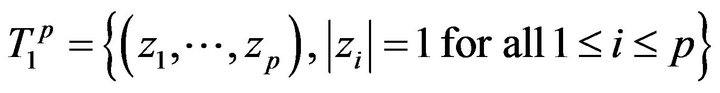
represent the torus in  and
and  the unit disc in
the unit disc in  if
if

and

For , we denote with
, we denote with  the integer part of the number
the integer part of the number  The addition and subtraction in
The addition and subtraction in , respectively in
, respectively in  are considered on components. In the set
are considered on components. In the set  the elements are treated in lexicographical order. If
the elements are treated in lexicographical order. If  is an arbitrary complex Hilbert space and
is an arbitrary complex Hilbert space and

a commuting multioperator, we denote by

for all  and, as usual,
and, as usual,  is the algebra of bounded operators on
is the algebra of bounded operators on ; also
; also 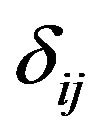 denotes the Kronecker symbol for
denotes the Kronecker symbol for . Let
. Let

be a sequence of bounded operators on  subject to the conditions
subject to the conditions 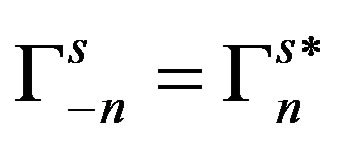 for all
for all

and  For such a finite sequence of operators, in [5], a necessary and sufficient condition for the existance of a a positive Borel operator-valued measure
For such a finite sequence of operators, in [5], a necessary and sufficient condition for the existance of a a positive Borel operator-valued measure  on
on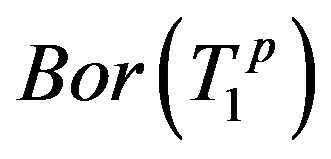 , such that the representations
, such that the representations
 (2.1.)
(2.1.)
hold, it is given. Such a measure is called a representing measure for 
In Section 3 of this note, in Proposition 3.1, we give a necessary and sufficient condition for the existence of an atomic representing measure of a truncated, operator-valued moment problem as in (2.1.) in case that the operators  act on a finite dimensional Hilbert space. In Proposition 3.2 of this note, the necessary and sufficient existence condition for the representing measure in (2.1.) is reformulated in terms of matrices.
act on a finite dimensional Hilbert space. In Proposition 3.2 of this note, the necessary and sufficient existence condition for the representing measure in (2.1.) is reformulated in terms of matrices.
In section 4, Proposition 4.2, we establish a RieszHerglotz formula for representing an analytic, operatorvalued function on , with real positive part in the class of operators. The obtained, representation formula for such functions is the same as in the scalar case [11, 12]. In this case, the representing measure is a positive operator-valued measure. The proof of Proposition 4.1 in this note is based on the characterization on an operatorsequence
, with real positive part in the class of operators. The obtained, representation formula for such functions is the same as in the scalar case [11, 12]. In this case, the representing measure is a positive operator-valued measure. The proof of Proposition 4.1 in this note is based on the characterization on an operatorsequence  to be a trigonometric, operator-valued moment sequence in [9]. The represented analytic, operator-valued function is the function which has as the Taylor’ s coefficients the operators
to be a trigonometric, operator-valued moment sequence in [9]. The represented analytic, operator-valued function is the function which has as the Taylor’ s coefficients the operators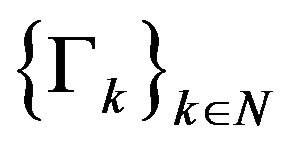 .
.
3. An Operator-Valued Truncated Trigonometric Moment Problem on Finite Dimensional Spaces
Let 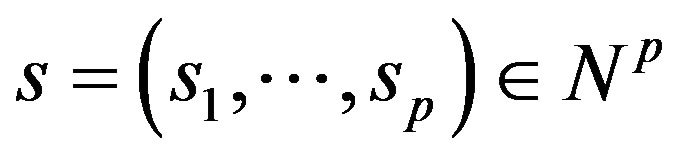 be arbitrary and consider the set
be arbitrary and consider the set

with the lexicographical order ( represents the cartesian product of the mentioned sets), H a finite dimensional Hilbert space with
represents the cartesian product of the mentioned sets), H a finite dimensional Hilbert space with
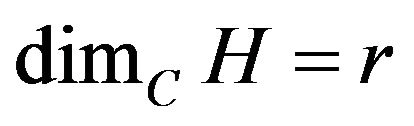 and
and 
Proposition 3.1. Let

be a sequence of bounded operators on 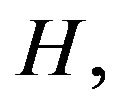 with
with
 for all
for all 
The following assertions are equivalent:
(i)  for all sequences
for all sequences  in
in 
(ii) There exists the multisequence

of  points and the bounded, positive operators,
points and the bounded, positive operators,  such that
such that
 (3.1)
(3.1)
for all 
(iii) There exists a positive atomic operator-valued measure  on
on  such that:
such that:

Proof.  On the set
On the set

we have the lexicographical order. The finite sequence of operators  is considered double indexed i.e.
is considered double indexed i.e.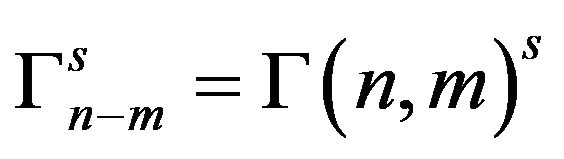 ; with this assumption, from
; with this assumption, from ,
,  can be viewed as an operator-valued kernel
can be viewed as an operator-valued kernel

Let  the C-vector space of functions defined on
the C-vector space of functions defined on  with values in the finite dimensional Hilbert space H. With the aid of
with values in the finite dimensional Hilbert space H. With the aid of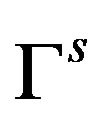 , we can introduce on
, we can introduce on  the non-negative hermitian product:
the non-negative hermitian product:

according to , we have the positivity condition:
, we have the positivity condition:

The matrix associated to this kernel is a Toeplitz matrix of the form:

From Kolmogorov’s theorem, there exists the Hilbert space (essentially unique) , obtained as the separate completeness of the
, obtained as the separate completeness of the  vector space of functions
vector space of functions 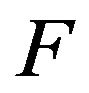 with respect to the usual norm generated on the set of cosets of Cauchy sequences, (i.e.
with respect to the usual norm generated on the set of cosets of Cauchy sequences, (i.e. ), by the nonnegative kernel
), by the nonnegative kernel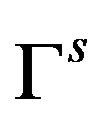 , respectively the space
, respectively the space 
(when H is finite dimensional, the Hilbert space
 ). From the same theorem, there also exists the sequence of operators
). From the same theorem, there also exists the sequence of operators 
such that  for all
for all  In this particular case for
In this particular case for , we have
, we have
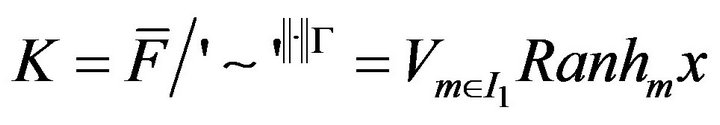
where  denotes the range of the operators
denotes the range of the operators  and
and  denotes the closed linear span of the sets
denotes the closed linear span of the sets ,
, . The operators
. The operators  are:
are:

with  and
and 
the Kronecker symbol. Also, from the construction of
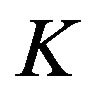 , we have
, we have , where
, where 
denotes the range of the operators  and
and  denotes the closed linear span of the sets
denotes the closed linear span of the sets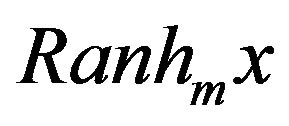 .
.
Let us consider the subsets

the subspaces in ,
,  ,
,  and the operators
and the operators 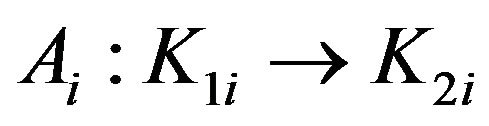 defined by the formula
defined by the formula

for any  with
with  the standard basis in
the standard basis in . From the definition of
. From the definition of , since
, since  are linear for all
are linear for all , the same is true for the operators
, the same is true for the operators  for all
for all . For an arbitrary
. For an arbitrary
 we have:
we have:

for all . We extend
. We extend  to
to  preserving the above definition and boundedness condition; the extensions
preserving the above definition and boundedness condition; the extensions  are denoted with the same letter
are denoted with the same letter 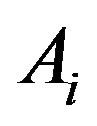 In case that
In case that

are C-linear independent operators with respect to the kernel , and from above, the operators
, and from above, the operators  are partial isometries, defined on linear closed subspaces
are partial isometries, defined on linear closed subspaces  with values in
with values in , with equal deficiency indices. In this case,
, with equal deficiency indices. In this case,  admit an unitary extension on the whole space
admit an unitary extension on the whole space  for all
for all  Let us denote the extensions of these operators to
Let us denote the extensions of these operators to  with the same letter
with the same letter . The adjoints of
. The adjoints of  are defined by
are defined by

for all  Obviously, for the extended operators
Obviously, for the extended operators 
In the same time, 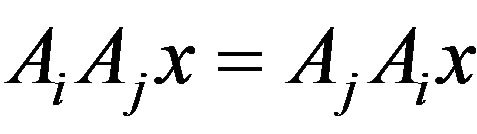 for all
for all  and all
and all ; we preserve the commuting relations for the extended operators. When
; we preserve the commuting relations for the extended operators. When  is a finite dimensional Hilbert space with a basis
is a finite dimensional Hilbert space with a basis , the same is true for the obtained Hilbert space
, the same is true for the obtained Hilbert space  All the vectors
All the vectors  are C-linear independent in
are C-linear independent in  with respect to the kernel
with respect to the kernel  Indeed, if
Indeed, if

equivalent with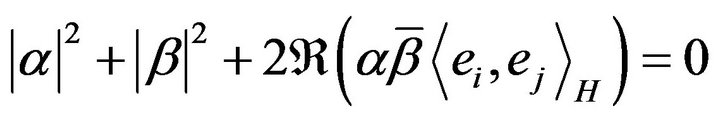 , this equality implies
, this equality implies  We consider that all the vectors
We consider that all the vectors  are C-linear independent in
are C-linear independent in  with respect to the kernel
with respect to the kernel  We have then,
We have then,
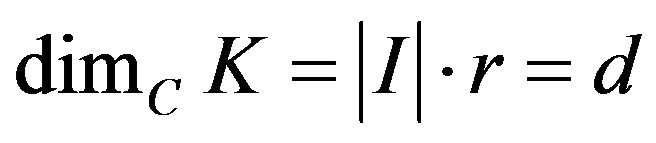 .
.
A basis in 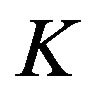 is
is

Let  be the defined isometries, with
be the defined isometries, with

and
 ;
;
for

and

We have  and also
and also  We consider
We consider  the orthonormal algebraic complement of the space
the orthonormal algebraic complement of the space 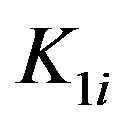 in
in , respectively
, respectively  the orthonormal complement of
the orthonormal complement of  When
When

for  and
and  when
when ; we have
; we have

Let 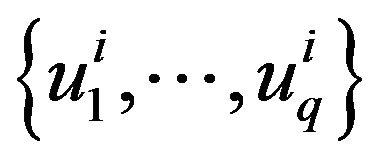 be an orthonormal basis in
be an orthonormal basis in respectively
respectively  an orthonormal basis in
an orthonormal basis in 
We extend the partial isometries 
 to the whole spaces
to the whole spaces  in the following way:
in the following way:

Because
 and
and

it results that also the extensions are isometries and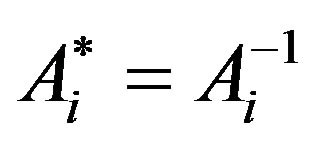 ; that is
; that is 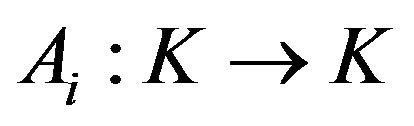 are unitary operators for all
are unitary operators for all ; ( the extended operators are denoted with the same letters). The commuting relations
; ( the extended operators are denoted with the same letters). The commuting relations  are also preserved
are also preserved  In the above conditions, the commuting multioperator
In the above conditions, the commuting multioperator 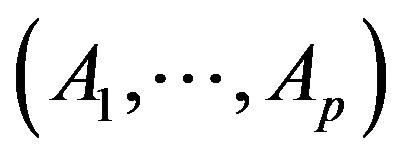 consisting of unitary operators on
consisting of unitary operators on  admits joint spectral measurewhose joint spectrum
admits joint spectral measurewhose joint spectrum  Considering the construction of
Considering the construction of , we obtain
, we obtain  and by induction
and by induction  for all
for all
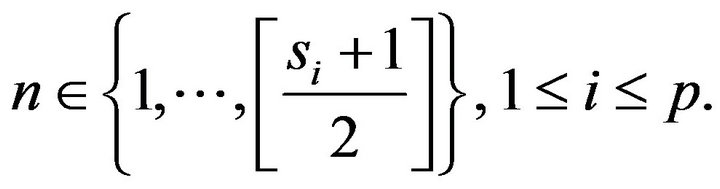
Because on the finite dimensional space , all the operators
, all the operators  are unitary and compact one, their spectrum
are unitary and compact one, their spectrum  consists only of the
consists only of the  principal values. The principal values are the roots of the characteristic polynomials associated with the matrix of
principal values. The principal values are the roots of the characteristic polynomials associated with the matrix of  in suitable basis in
in suitable basis in , for all
, for all 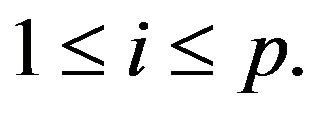 The characteristic polynomials of
The characteristic polynomials of  are all complex variable polynomials of the same degree
are all complex variable polynomials of the same degree

with the roots 
Let , be the family of the spectral projectors associated with the families of the principal values
, be the family of the spectral projectors associated with the families of the principal values  that is
that is  with
with 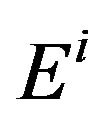 the spectral measures of
the spectral measures of  From the definition of
From the definition of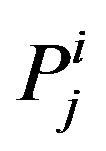 , we have
, we have  for all
for all
 and
and  Because
Because
 we have also
we have also

Consequently, for , we have obtain:
, we have obtain:
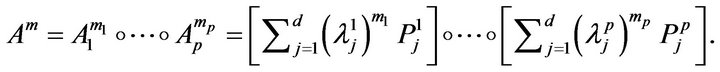
From Kolmogorov’s decomposition theorem for , we have
, we have

with 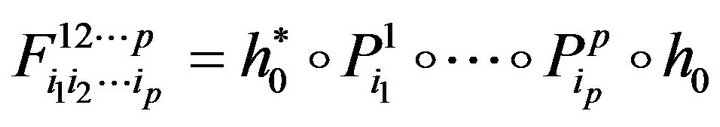 positive operators. That is:
positive operators. That is:
 (3.2.)
(3.2.)
(i.e. assertion )
)
 Let
Let  be a positive, atomic operator-valued measure on
be a positive, atomic operator-valued measure on . From
. From  we have:
we have:

(i.e. assertion (iii)).
 If
If

and  is a positive operator-valued measure, we have:
is a positive operator-valued measure, we have:

that is 
Proposition 3.1, in case H a finite dimensional space, statements  implies also a similar, straightforward characterization, as in the scalar case [6]:
implies also a similar, straightforward characterization, as in the scalar case [6]:
Proposition 3.2. When
 operators acting on a finite dimensional space
operators acting on a finite dimensional space  with
with , are as in Proposition 1, the Toeplitz matrix
, are as in Proposition 1, the Toeplitz matrix

is positive semidefinite if and only if it can be factorized as 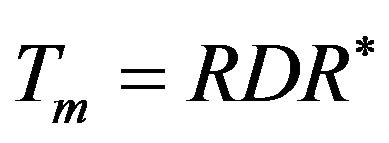 with
with

 the diagonal matrix
the diagonal matrix

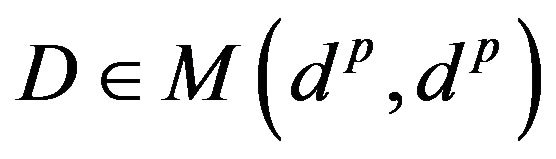 with entries the positive operators
with entries the positive operators
 on the principal diagonal.
on the principal diagonal.
4. A Riesz-Herglotz Formula for Operator-Valued, Analytic Functions on the Unit Disk
Remark 4.1. Let  be a sequence of bounded operators, acting on an arbitrary, separable, complex Hilbert space
be a sequence of bounded operators, acting on an arbitrary, separable, complex Hilbert space , such that
, such that  for all
for all  and
and  The following statements are equivalent:
The following statements are equivalent:
(a)  for all
for all  and all sequences of complex numbers
and all sequences of complex numbers  with only finite nonzero terms.
with only finite nonzero terms.
(b) There exists a positive, operator-valued measure  on
on  such that
such that
 .
.
(c) The operator kernel  is positive semidefinite on
is positive semidefinite on , that is it satisfies
, that is it satisfies

for all , all sequences of vectors
, all sequences of vectors  and all
and all 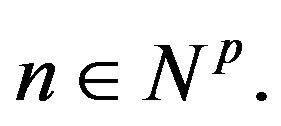
Proof. (a)  (b) was solved in [9], Corollary 1.4.10.
(b) was solved in [9], Corollary 1.4.10.
(b)  (c) represents the sufficient condition in Proposition 1, [10].
(c) represents the sufficient condition in Proposition 1, [10].
(c)  (a). Let
(a). Let  with
with  for an arbitrary
for an arbitrary  From (c), it results
From (c), it results

that is the operator kernel satisfies

(that is statement (a)).
Because the trigonometric polynomials are uniformly dense in the space of the continuous functions on  it results that the representing measure of the operator moment sequence is unique.
it results that the representing measure of the operator moment sequence is unique.
For the proof of the following Proposition 4.2, we recall some observations.
A bounded monotonic sequence of positive non-negative operators converges in the strong operator topology to a non-negative operator (pp. 233, [11]). Due to this remark, if  is a continuous, positive operator-valued function on the compact set
is a continuous, positive operator-valued function on the compact set , we define the Riemann integral of the function
, we define the Riemann integral of the function  with respect to the Lebesgue measure
with respect to the Lebesgue measure  The definition are the usual one in the class of positive operators. That is: the limits of the riemannian sums associated to the function
The definition are the usual one in the class of positive operators. That is: the limits of the riemannian sums associated to the function , arbitrary divisions
, arbitrary divisions  of
of  and arbitrary intermediar points
and arbitrary intermediar points  exists (are limits of bounded monotonic sequence of non-negative operators), and from the continuity assumption of
exists (are limits of bounded monotonic sequence of non-negative operators), and from the continuity assumption of  on the compact set
on the compact set , are all the same. We denote the common limits, as usual with
, are all the same. We denote the common limits, as usual with  We apply this natural construction in the proof of the following result.
We apply this natural construction in the proof of the following result.
Proposition 4.2. Let  be an analytic, vectorial function, with values in the set of bounded operators on a complex, separable Hilbert space
be an analytic, vectorial function, with values in the set of bounded operators on a complex, separable Hilbert space . The following statements are equivalent:
. The following statements are equivalent:
(a) 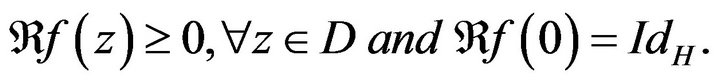
(b) (Riesz-Herglotz formula) There exists a positive operator-valued measure  on
on  with
with

and an operator  such that:
such that:

The proof follows quite the similar steps as the proof of the Riesz-Herglotz formula for analytic, scalar functions with real positive part ([11,12].)
Proof. (a)  (b) Let
(b) Let

be the Taylor expansion of ,
,  with
with
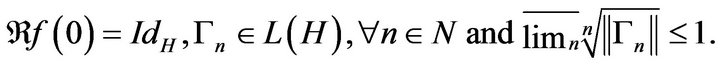
We define  for all
for all  In this case , we obtain for all
In this case , we obtain for all ,
,

If we consider  arbitrary and
arbitrary and
 , the previous equality becomes
, the previous equality becomes

As a consequence of the orthogonality of the system of functions  with respect to the usual scalar product defined on
with respect to the usual scalar product defined on , from the the previous remark and
, from the the previous remark and  s uniform convergent expansions, for all sequences
s uniform convergent expansions, for all sequences  and all
and all  we obtain:
we obtain:

We normalize this relation by dividing it with 2 and obtain, for , the following inequalities:
, the following inequalities:
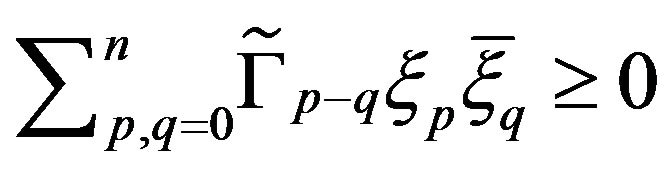
for all sequences  and all arbitrary
and all arbitrary with
with
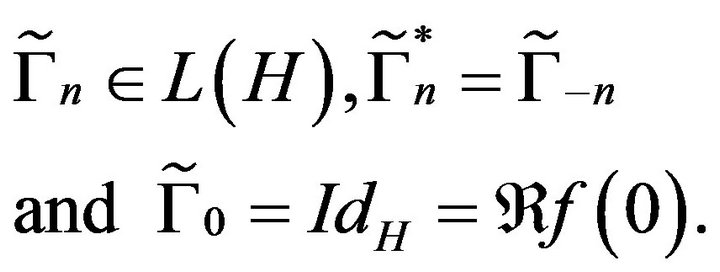
In the above conditions from Theorem 1.4.8, [9], there exists a positive operator-valued measure  on
on  such that
such that

For  and
and  we have
we have 
Let the homeomorphism  and the positive operator-valued measure
and the positive operator-valued measure

Accordingly to this measure we obtain the representations:
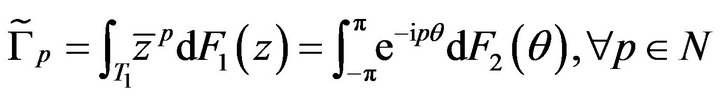
and

Assured by the integral representations of the operators 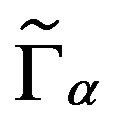 we have:
we have:



 is analytic on
is analytic on ,
, 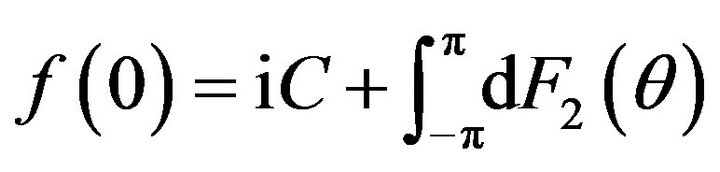 and
and 
For the operator-valued analytic functions on  we can state the same characterization theorem as in the the scalar case ( Theorem 3.3, [11],) that is:
we can state the same characterization theorem as in the the scalar case ( Theorem 3.3, [11],) that is:
Theorem 4.3. Let  be a sequence of bounded operators acting on an arbitrary, separable, complex Hilbert space
be a sequence of bounded operators acting on an arbitrary, separable, complex Hilbert space , subject to the conditions
, subject to the conditions 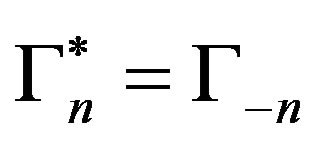 for all
for all ,
,  The following statements are equivalent:
The following statements are equivalent:
(a) There exists an unique, positive, operator-valued measure  on
on  such that:
such that:
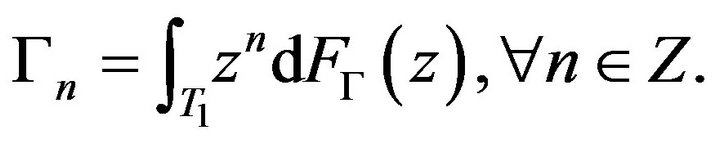
(b) The Toeplitz matrix  is positive semidefinite.
is positive semidefinite.
(c) There exists an analytic vectorial function  for all
for all  and
and

for some  with
with 
(d) There exists a separable, Hilbert space , an operator
, an operator  and an unitary operator
and an unitary operator , such that
, such that 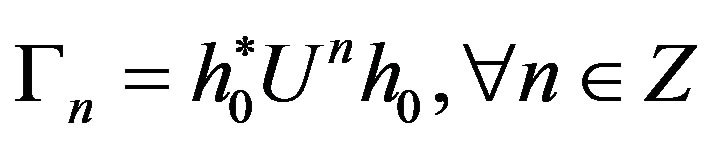 and
and 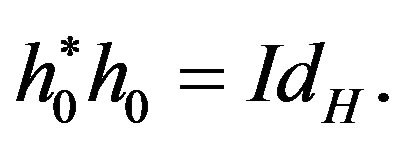
Proof.  was solved in [9], Th.1.4.8., p. 188. We sketch the proof of implication
was solved in [9], Th.1.4.8., p. 188. We sketch the proof of implication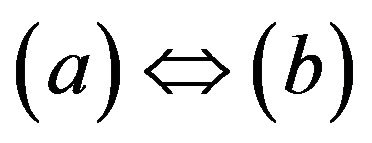 .
.
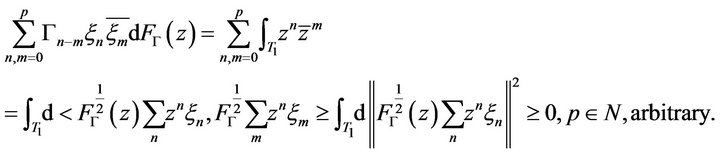
 As in above Proposition 4.2, there exists a positive operator-valued measure
As in above Proposition 4.2, there exists a positive operator-valued measure 
such that 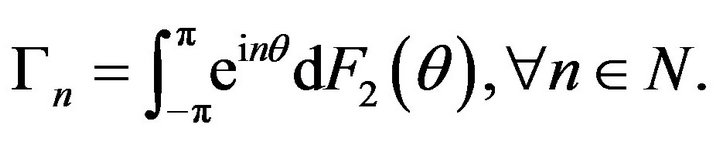 In this case, for the function
In this case, for the function , we have
, we have
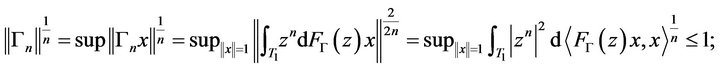
that is  is analytic on
is analytic on  Also from (a), we have:
Also from (a), we have:
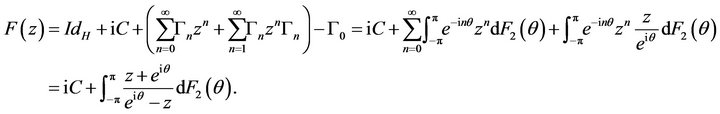
From the above representation, it results:

(c)  (a) As the same proof in Proposition 4.2, we have
(a) As the same proof in Proposition 4.2, we have

for arbitrary . From this inequality, it results that there exist the representations
. From this inequality, it results that there exist the representations 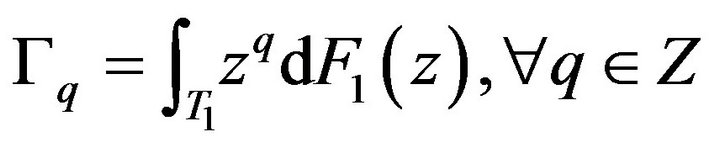
with  a positive operator valued measure on
a positive operator valued measure on  ([9], Th. 1.3.2), this is (a).
([9], Th. 1.3.2), this is (a).
The equivalence, . From remark 4.1.we have
. From remark 4.1.we have  ((c) from Remark 4.1.). The equivalence
((c) from Remark 4.1.). The equivalence  is the main result in [10], Proposition 1. p. 116. From [10], Proposition 1, (condition (c) in Remark 4.1.) assured the existence of a Hilbert space
is the main result in [10], Proposition 1. p. 116. From [10], Proposition 1, (condition (c) in Remark 4.1.) assured the existence of a Hilbert space , an operator
, an operator  and an unitary operator
and an unitary operator  such that
such that , that is (d); (the Hilbert Space
, that is (d); (the Hilbert Space , the unitary operator
, the unitary operator  are obtained by applyng Kolmogorov’s decomposition theorem on positive semidefinite kernels.) Conversely
are obtained by applyng Kolmogorov’s decomposition theorem on positive semidefinite kernels.) Conversely  is immediately.
is immediately.
5. Conclusion
We give a necessary and sufficient condition on a finite sequence of bounded operators, acting on a finite dimensional Hilbert space, to admit an integral representation as complex moment sequence with respect to an atomic, positive, operator-valued measure. We also established a Riesz-Herglotz representation formula for operator-valued, analytic functions on the unit disc, with real positive part in the class of operators.