Hyers-Ulam Stability of a Generalized Second-Order Nonlinear Differential Equation ()
1. Introduction
In 1940 Ulam posed the basic problem of the stability of functional equations: Give conditions in order for a linear mapping near an approximately linear mapping to exist [1]. The problem for approximately additive mappings, on Banach spaces, was solved by Hyers [2]. The result obtained by Hyers was generalized by Rassias [3].
After then, many mathematicians have extensively investigated the stability problems of functional equations (see [4-6]).
Alsina and Ger [7] were the first mathematicians who investigated the Hyers-Ulam stability of the differential equation 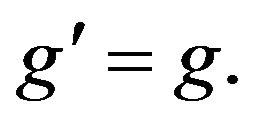 They
They proved that if a differentiable function
proved that if a differentiable function 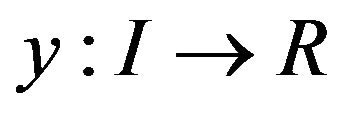 satisfies
satisfies  for all
for all  then there exists a differentiable function
then there exists a differentiable function  satisfying
satisfying  for any
for any  such that
such that  for all
for all . This result of alsina and Ger has been generalized by Takahasi et al [8]
. This result of alsina and Ger has been generalized by Takahasi et al [8] to the case of the complex Banach space valued differential equation
to the case of the complex Banach space valued differential equation 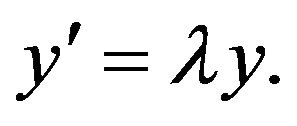
Furthermore, the results of Hyers-Ulam stability of differential equations of first order were also generalized by Miura et al. [9], Jung [10] and Wang et al. [11].
Motivation of this study comes from the work of Li [12] where he established the stability of linear differential equation of second order in the sense of the Hyers and Ulam  Li and Shen [13] proved the stability of nonhomogeneous linear differential equation of second order in the sense of the Hyers and Ulam
Li and Shen [13] proved the stability of nonhomogeneous linear differential equation of second order in the sense of the Hyers and Ulam 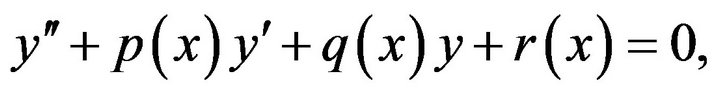 while Gavruta et al. [14] proved the Hyers-Ulam stability of the equation
while Gavruta et al. [14] proved the Hyers-Ulam stability of the equation  with boundary and initial conditions.
with boundary and initial conditions.
The author in his study [15] estabilshed the HyersUlam stability of the equations of the second order

and

with the initial conditions 
In this paper we investigate the Hyers-Ulam stability of the following nonlinear differential equation of second order
 (1)
(1)
with the initial condition
 (2)
(2)
where

Moreover we investigate the Hyers-Ulam stability of the Emden-Fowler nonlinear differential equation of second order
 (3)
(3)
with the initial condition
 (4)
(4)
where

and  is bounded in
is bounded in .
.
Definition 1.1 We will say that the Equation (1) has the Hyers-Ulam stability if there exists a positive constant  with the following property:
with the following property:
For every , if
, if
 (5)
(5)
with the initial condition (2), then there exists a solution  of the Equation (1), such that
of the Equation (1), such that
 .
.
Definition 1.2 We say that Equation (3) has the HyersUlam stability with initial conditions (4) if there exists a positive constant 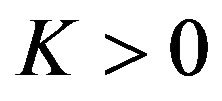 with the following property:
with the following property:
For every , if
, if
 (6)
(6)
and , then there exists some
, then there exists some
 satisfying
satisfying  and
and
 , such that
, such that .
.
2. Main Results on Hyers-Ulam Stability Theorem 2.1 If  is
is such that
such that
 and
and 
then the Equation (1) is stable in the sense of Hyers and Ulam.
Proof. Let
Let  and
and  be a twice continuously differentiable real-valued function on
be a twice continuously differentiable real-valued function on  We will show that there exists a function
We will show that there exists a function  satisfying Equation (1) such that
satisfying Equation (1) such that

where  is a constant that never depends on
is a constant that never depends on  nor on
nor on  Since
Since  is a continuous function on
is a continuous function on  then it keep its sign on some interval
then it keep its sign on some interval 
Without loss of generality assume that  on
on  Assume that
Assume that 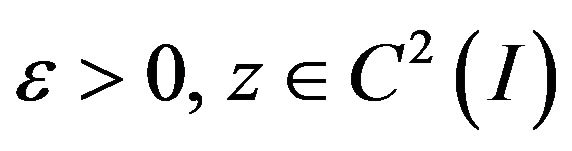 satisfies the inequation (5) with the initial conditions (2) and that
satisfies the inequation (5) with the initial conditions (2) and that

From the inequality (5) we have
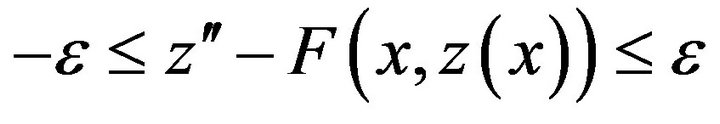 (7)
(7)
Since  on
on  and
and  then by Mean Value Theorem
then by Mean Value Theorem  in
in . Multiplying the inequality (7) by
. Multiplying the inequality (7) by 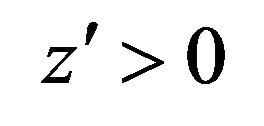 and then integrating from
and then integrating from  to
to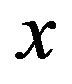 , we obtain
, we obtain

Since  we get that
we get that
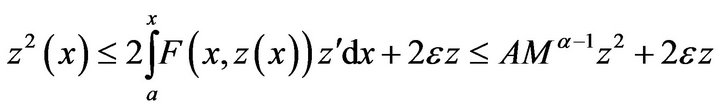
Therefore

Hence  for all
for all  Obviously,
Obviously,  satisfies the Equation (1) and the zero initial condition (2) such that
satisfies the Equation (1) and the zero initial condition (2) such that

Hence the Equation (1) has the Hyers-Ulam stability with initial condition (2).
Remark 2.1 Suppose that  satisfies the inequality (5) with the initial condition (2). If
satisfies the inequality (5) with the initial condition (2). If

then, if

we can similarly show that the Equation (1) has the Hyers-Ulam stability with initial condition (2).
Theorem 2.2 Suppose that  is a twice continuously differentiable function and
is a twice continuously differentiable function and .
.
If  then the Equation (3) is stable in the sense of Hyers and Ulam.
then the Equation (3) is stable in the sense of Hyers and Ulam.
Proof. Let
Let  and
and  be a twice continuously differentiable real-valued function on
be a twice continuously differentiable real-valued function on  We will show that there exists a function
We will show that there exists a function  satisfying Equation (3) such that
satisfying Equation (3) such that

where  is a constant that never depends on
is a constant that never depends on  nor on
nor on  Since
Since  is a continuous function on
is a continuous function on 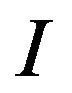 then it keeps its sign on some interval
then it keeps its sign on some interval  Without loss of generality assume that
Without loss of generality assume that  on
on 
Suppose that  satisfies the inequation (6) with the initial conditions (4) and that
satisfies the inequation (6) with the initial conditions (4) and that
 We have
We have
 (8)
(8)
Since  in
in  then, Multiplying the inequality (8) by
then, Multiplying the inequality (8) by  and integrating, we obtain
and integrating, we obtain

By hypothesis , so we get that
, so we get that

Therefore

Hence  for all
for all  Clearly, the zero function
Clearly, the zero function  satisfies the
satisfies the Equation (1) and the zero initial condition (2) such that
Equation (1) and the zero initial condition (2) such that

Hence the Equation (3) has the Hyers-Ulam stability with initial condition (4).
Remark 2.2 Suppose that  satisfies the inequality (6) with the initial condition (4). If
satisfies the inequality (6) with the initial condition (4). If
 then, if
then, if 
we can similarly show that the Equation (3) has the Hyers-Ulam stability with initial condition (4).
Example 2.2 Consider the equation
 (9)
(9)
and the inequality
 (10)
(10)
where 
It should be noted that for a given  satisfies the inequation (10) and the conditions of the Theorem 2.2. Therefore the Equation (9) has the HyersUlam stability.
satisfies the inequation (10) and the conditions of the Theorem 2.2. Therefore the Equation (9) has the HyersUlam stability.
3. A Special Case of Equation (3)
Consider the special case (when ) of the Equation (3)
) of the Equation (3)
 (11)
(11)
with the initial conditions
 (12)
(12)
and the inequation
 (13)
(13)
where 
Theorem 3.1 Assume that  is a twice continuously differentiable function and
is a twice continuously differentiable function and  Then, If
Then, If  the Equation (11) is stable in the sense of Hyers and Ulam.
the Equation (11) is stable in the sense of Hyers and Ulam.
Proof. Assume that  and
and that
that  is a twice continuously differentiable real-valued function on
is a twice continuously differentiable real-valued function on  We will show that there exists a function
We will show that there exists a function  satisfying Equation (11) such that
satisfying Equation (11) such that

where  is a constant that never depends on
is a constant that never depends on  nor on
nor on 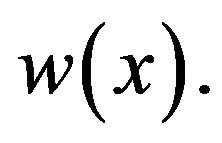 Since
Since  is a continuous function on
is a continuous function on  then it keeps its sign on some interval
then it keeps its sign on some interval  Without loss of generality assume that
Without loss of generality assume that  on
on  Suppose that
Suppose that  satisfies the inequation (13) with the initial conditions (12).
satisfies the inequation (13) with the initial conditions (12).
We have
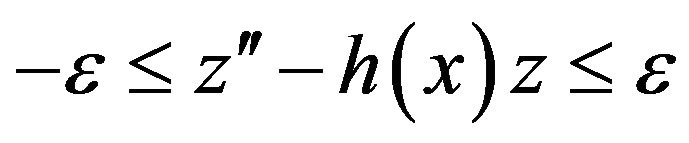 (14)
(14)
Applying the Mean Value Theorem to the function  on the interval
on the interval 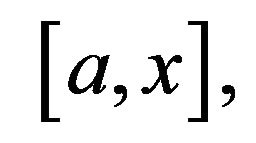 we find that
we find that  in
in . Multiplying the inequality (14) by
. Multiplying the inequality (14) by  and then integrating we obtain
and then integrating we obtain

If , we obtain the inequality
, we obtain the inequality

Therefore

Thus  for all
for all  The zero solution
The zero solution  of the
of the Equation (11) with the zero initial condition (12) such that
Equation (11) with the zero initial condition (12) such that
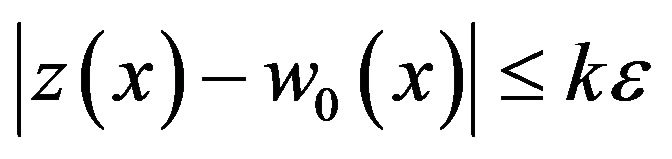
Hence the Equation (11) has the Hyers-Ulam stability with initial condition (12).
Remark 3.1 Assume that  satisfies the inequality (13) with the initial condition (12). If
satisfies the inequality (13) with the initial condition (12). If  then, if
then, if  we can similarly obtain the Hyers-Ulam stability criterion for the Equation (11) has with initial condition (12).
we can similarly obtain the Hyers-Ulam stability criterion for the Equation (11) has with initial condition (12).
Remark 3.2 It should be noted that if  on
on  and
and  hence
hence 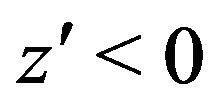 on
on  then in the proofs of Theorem 2.1, 2.2 and 3.1, we can multiply by
then in the proofs of Theorem 2.1, 2.2 and 3.1, we can multiply by  the inequation (7) (and (8), (14)) to obtain the inequality
the inequation (7) (and (8), (14)) to obtain the inequality

Then we can apply the same argument used above to get sufficient criteria for the Hyers-Ulam stability for the Equations (1), (3) and (11).
Example 3.1 Consider the equation
 (15)
(15)
and the inequality
 (16)
(16)
where 
First it should be noted that for a given ,
,  satisfies the inequation (16) and the conditions of the Theorem 3.1. Therefore the Equation (15) has the Hyers-Ulam stability.
satisfies the inequation (16) and the conditions of the Theorem 3.1. Therefore the Equation (15) has the Hyers-Ulam stability.
4. An Additional Case On Hyers-Ulam Stability
In this section we consider the Hyers-Ulam stability of the following equation
 (17)
(17)
with the initial condition
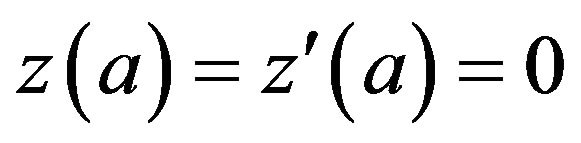 (18)
(18)
where

and  is continuous for
is continuous for 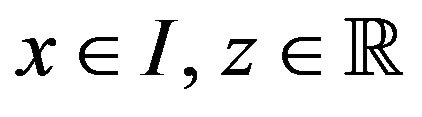 such that
such that

Using an argument similar to that used in [16], we can prove the following Theorem:
Theorem 4.1 Suppose that  is a twice continuously differentiable function.
is a twice continuously differentiable function.
If  then the problem (17), (18) is stable in the Hyers-Ulam sense.
then the problem (17), (18) is stable in the Hyers-Ulam sense.
Proof. Let
Let  and
and be a twice continuously differentiable real-valued function on
be a twice continuously differentiable real-valued function on 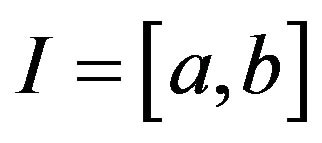 satisfying the inequality
satisfying the inequality
 (19)
(19)
We will show that there exists a function
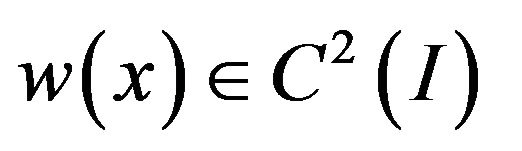
Satisfying Equation (18) such that

where  is a constant that doesn’t depend on
is a constant that doesn’t depend on  nor on
nor on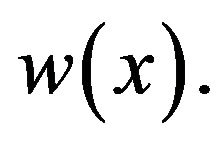 If we integrate the inequality (19) with respect to
If we integrate the inequality (19) with respect to  we should obtain
we should obtain
 (20)
(20)
It is clear that  is a solution of the Equation (21)
is a solution of the Equation (21)
 (21)
(21)
satisfying the zero initial condition
 (22)
(22)
Now, let’s estimate the difference

Since the function  satisfies the Lipschitz condition, and from the inequality (20) we have
satisfies the Lipschitz condition, and from the inequality (20) we have

From which it follows that

where  Hence the problem (17), (18) has the Hyers-Ulam stability.
Hence the problem (17), (18) has the Hyers-Ulam stability.
Remark 4.1 Notice that if  satisfies Lipschitz condition
satisfies Lipschitz condition in the region
in the region  then the Emden-Fowler nonlinear differential equation
then the Emden-Fowler nonlinear differential equation  is Hyers-Ulam stable with zero initial condition.
is Hyers-Ulam stable with zero initial condition.
5. Acknowledgements
The author thanks the anonymous referees for helpful comments and suggestions.