Hamiltonian Polynomial Eigenvalue Problems

Mustapha Bassour^1,2

¹Faculté des Sciences Juridiques, Economiques et Sociales, Ait Melloul, Morocco.
²LISTI Laboratory ENSA, Ibn Zohr University, Agadir, Morocco.

DOI: 10.4236/jamp.2020.84047                

Abstract

We present in this paper a new method for solving polynomial eigenvalue problem. We give methods that decompose a skew-Hamiltonian matrix using Cholesky like-decomposition. We transform first the polynomial eigenvalue problem to an equivalent skew-Hamiltonian/Hamiltonian pencil. This process is known as linearization. Decomposition of the skew-Hamiltonian matrix is the fundamental step to convert a structured polynomial eigenvalue problem into a standard Hamiltonian eigenproblem. Numerical examples are given.

Keywords

Hamiltonian Matrix, Polynomial Eigenvalue Problem, Skew-Hamiltonian/Hamiltonian Pencil, Cholesky Like-Decomposition

1. Introduction

In this work we propose a numerical approach for solving the k^th degree polynomial eigenvalue problem

$P\left(\lambda \right)v={\displaystyle \underset{i=0}{\overset{k}{\sum }}}{\lambda }^i{M}_{i}v=0$ (P)

Problem (P) arises in many applications in science and engineering, ranging from the dynamical analysis of structural systems such as bridges and buildings to theories of elementary particles in atomic physics [1] [2]. It’s also the most important task in the vibration analysis of buildings, machines, and vehicles [3]. We first transform our k^th degree polynomial eigenvalue problem (P) to an equivalent first-degree equation $\left(A-\lambda B\right)v=0$ commonly called pencil problem. In the case when matrices $M_i$ have symmetric/skew-symmetric structure, the problem (P) is transformed to a skew-Hamiltonian/Hamiltonian pencil [4]. The second step is to transform the skew-Hamiltonian/Hamiltonian pencil to a standard Hamiltonian eigenproblem $Hv=\lambda v$ [5]. This transformation is obtained after decomposing B as $R^{\text{T}}JR$ where R is a permuted triangular matrix.

The Hamiltonian matrix H is given by $J^{\text{T}}{R}^{-\text{T}}A{R}^{-1}$ where $J=\left(\begin{array}{cc}0& I_n\\ -I_n& 0\end{array}\right)$.

It is known that any nonsingular skew-symmetric matrix has a decomposition of the form $B=R^{\text{T}}JR$ [6]. The real matrix $M=J^{\text{T}}B$ is skew-Hamiltonian and has the decomposition $J^{\text{T}}B=R^{\text{J}}R$ where R has the form of a permuted triangular matrix. We give here a new proof for this result and different algorithms that compute the decomposition $M=R^{\text{J}}R$.

2. Preliminaries

We give in this paragraph, new definitions and useful propositions.

Let $J=J_{2n}=\left(\begin{array}{cc}0& I_n\\ -I_n& 0\end{array}\right)$, where $I_n$ denotes the $n\times n$ identity matrix. We

will use J when the size is clear from the context. Recall that a matrix $M\in {ℝ}^{2n\times 2n}$ is skew-Hamiltonian if $M^J=M$, where the J-transpose of the matrix M is defined

by $M^J=J^T{M}^{\text{T}}J$. Likewise, a Hamiltonian matrix H is written as $\left(\begin{array}{cc}E& G\\ F& -E^{\text{T}}\end{array}\right)$

where E, G and $T\in {ℝ}^{n\times n}$ with $G^{\text{T}}=G$ and $F^{\text{T}}=F$. We have $H^J=-H$. More general, the J-transpose of the rectangular 2p-by-2q matrix N is defined by 2q-by-2p matrix $N^J=J_{2q}^{\text{T}}{N}^{\text{T}}{J}_{2p}$.

The set ${\left(E_i\right)}_{1\le i\le n}$ where $E_i=\left[e_i{e}_{n+i}\right]$ with $e_i$ is denoting the i-th unit vector of length 2n, satisfies $E_i{J}_2=J_{2n}{E}_i$, $E_i^J=E_i^{\text{T}}$ and $E_i^{\text{T}}{E}_j={\delta }_{ij}{I}_2$ where $E_i^J=J_2^{\text{T}}{E}_i^{\text{T}}{J}_{2n}$ and ${\delta }_{ij}=\{\begin{array}{l}1\text{if}i=j\\ 0\text{if}i\ne j\end{array}$

Let $U=\left[u_1,u_2\right]\in R^{2n\times 2}$ where $u_1={\displaystyle \underset{i=1}{\overset{2n}{\sum }}}{u}_i^1{e}_i$ and $u_2={\displaystyle \underset{j=1}{\overset{2n}{\sum }}}{u}_j^2{e}_j$. Then U is written in a unique way as linear combination of ${\left(E_i\right)}_{1\le i\le n}$ on ${ℝ}^{2\times 2}$, $U=\stackrel{n}{\underset{i=1}{{\displaystyle \sum }}}{E}_i{M}_i$ where $M_i=\left(\begin{array}{cc}{u}_i^1& u_i^2\\ u_{n+i}^1& u_{n+i}^2\end{array}\right)$. Let $M\in {ℝ}^{2n\times 2n}$ be a 2n-by-2n real matrix. Then M is written as $M=\stackrel{n}{\underset{i=1}{{\displaystyle \sum }}}\stackrel{n}{\underset{j=1}{{\displaystyle \sum }}}{E}_i{M}_{ij}{E}_j^{\text{T}}$ where $M_{ij}=\left(\begin{array}{cc}{m}_{ij}& m_{i\mathrm{,}n+j}\\ m_{n+i\mathrm{,}j}& m_{n+i\mathrm{,}n+j}\end{array}\right)$.

Definition 2.1. The 2n-by-2n real matrix $L={\displaystyle \underset{i=1}{\overset{n}{\sum }}}{\displaystyle \underset{j=1}{\overset{n}{\sum }}}{E}_i{L}_{ij}{E}_j^{\text{T}}$ is called lower J-triangular if $L_{ij}=0_{2\times 2}$ for $j>i$ and $L_{ii}=\left(\begin{array}{cc}\ast & 0\\ \ast & \ast \end{array}\right)$, (i.e., $L={\displaystyle \underset{i=1}{\overset{n}{\sum }}}{\displaystyle \underset{j=1}{\overset{i}{\sum }}}{E}_i{L}_{ij}{E}_j^{\text{T}}$ ).

Definition 2.2. The 2n-by-2n real matrix $U={\displaystyle \underset{i=1}{\overset{n}{\sum }}}{\displaystyle \underset{j=1}{\overset{n}{\sum }}}{E}_i{U}_{ij}{E}_j^{\text{T}}$ is called upper J-triangular if $U_{ij}=0_{2\times 2}$ for $i>j$ and $U_{ii}=\left(\begin{array}{cc}\ast & \ast \\ 0& \ast \end{array}\right)$, (i.e., $U={\displaystyle \underset{i=1}{\overset{n}{\sum }}}{\displaystyle \underset{j=i}{\overset{n}{\sum }}}{E}_i{U}_{ij}{E}_j^{\text{T}}$ ).

Proposition 2.1. Let M and N be two upper J-triangular (respectively, lower J-triangular) 2n-by-2n real matrix. The product 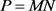remain as upper J-triangular (respectively, as lower J-triangular).

Proof. Let and 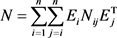two upper J-triangular 2n-by-2n real matrix. The matrix product of M and N is obtained by

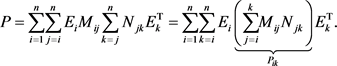
That proves 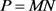remain as upper J-triangular. (similarly, when M and N are lower J-triangular).

Definition 2.3. 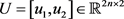is called J-isotropic if .

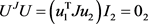Proposition 2.2. The inverse of a regular upper J-triangular 2n-by-2n real matrix (respectively, lower J-triangular) is also upper J-triangular (respectively, also lower J-triangular).

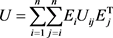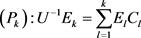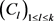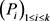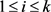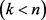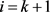Proof. Let an upper J-triangular 2n-by-2n real matrix. The following proposition, where are 2-by-2 real matrix, holds for. Suppose are true for,. For, we have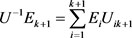, therefore

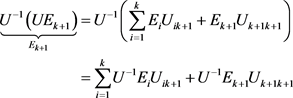
Since is invertible and by using recurrence hypothesis, then

with.

3. Cholesky Like-Decomposition for Skew-Hamiltonian Matrix

In this section, we study different ways to compute decomposition of a real skew-Hamiltonian matrix. We began first by giving some interesting theoretical results.

3.1. Definition and Theoretical Results

Definition 3.1. The 2n-by-2n real skew-Hamiltonian matrix M is called J-definite if with for every non J-isotropic (i.e.,).

Remark 3.1 For and a 2n-by-2n real skew-Hamiltonian matrix M, with.

Lemma 3.1. If M is a 2n-by-2n real skew-Hamiltonian and J-definite matrix, then M is invertible.

Proof. If not, there exists such that. Let that verify non J-isotropic (i.e.,). Since, then which is contradictory with the hypothesis.

Theorem 3.2. If M is a 2n-by-2n real skew-Hamiltonian, J-definite matrix, then M has an LU J-factorization.

Proof. Let () be non J-isotropic. Suppose that where. We construct an such that where for. We have, where as defined in theorem 2.2 given above. Then 2k-by-2k matrix remains skew-Hamiltonian and J-definite and then invertible.

Corollary 3.3. If is the LU J-factorization of the real 2n-by-2n skew-Hamiltonian, J-definite matrix M, then M has an where

(here is the i-th diagonal entry of U).

Proof. Since the matrix M is skew-Hamiltonian, then by taking we obtain

is nothing but the J-factorization of M. Indeed, is lower J-triangular with 1 in diagonal and is upper J-triangular. Thus, from the uniqueness of the J-factorization, it follows that.

Theorem 3.4. Let M be a 2n-by-2n real skew-Hamiltonian J-definite matrix, then M has a Cholesky J-factorization where N is lower J-triangular

and in addition the are diagonal.

Proof. We proceed by induction on n. For, the real 2-by-2 skew-Hamiltonian J-definite matrix where. If we set , the theorem holds trivially.

Let’s now. Since M is skew-Hamiltonian and J-definite, then. We can write

We set and. The J-transpose of W is given by. Let, and. We calculate. The J-transpose of is given by. Finally, we obtain

Since, then. By induction , where where L is -by- lower J-triangular matrix and in addition the are diagonal for. Therefore, if we let, we obtain and then finally

Since and G are lower J-triangular, then remain lower J-triangular and verify are diagonal.

3.2. Method 1

We construct an algorithm that gives decomposition of skew-Hamiltonian matrices via a J-decomposition.

Proposition 3.5. Let M is a 2n-by-2n real skew-Hamiltonian, J-definite matrix. If its J-factorization, then where D is a diagonal matrix defined by

(here is the i-th diagonal entry of U) is lower J-triangular and verify.

Proof. By corollary 3.3,. Since where D is as given above, then is lower J-triangular and . From the J-decomposition given by algorithms in section, we set

where. We have where.

3.3. Method 2

We study now a method that constructs decomposition of skew-Hamiltonian J-definite matrices.

Let be a skew-Hamiltonian J-definite matrix.

with and. Let where L is lower J-triangular that verify. The existence of L is guaranteed by theorem 4.4

Since

then

If, then. We obtain. Since and, then, then

And for,. Multiplying on the right by, we obtain

Thus

Since

then,

Since, then

If we set, then we obtain

However for, then. Multiplying on the right by we find and finally.

The method yield the following algorithm.

Algorithm:

for

for

4. Polynomial Eigenvalue Problems

Many applications give rise to structured matrix polynomial eigenvalue problems

The numerical solution of this polynomial eigenvalue problem is one of the most important tasks in the vibration analysis of buildings, machines and vehicles [7]. In many applications, the coefficient matrices have particular structure and it is important that numerical methods respect this structure. A popular approach for solving the polynomial eigenvalue problem is to linearize to produce a generalized eigenproblem [8].

Theorem 4.1. [9] Consider the polynomial eigenvalue problem with either or and with nonsingular. Then solving problem is equivalent to solve where

and

We draw from this theorem that the polynomial eigenvalue problem (P) can be reduced to an eigenvalue pencil problem where A is symmetric and B is skew-symmetric. The second step is to transform the skew-symmetric/ symmetric pencil to a standard Hamiltonian eigenproblem by decomposing the skew-Hamiltonian matrix as. The Hamiltonian matrix H is then obtained by. Eigenvalue problems of this type arise property that all eigenvalues appear in quadruples, the spectrum is symmetric with respect to the real and imaginary axes.

5. Numerical Examples

We present computed eigenvalues that solve the k^th degree polynomial eigenvalue problem of dimension which is transforming to a standard eigenvalue problem of dimension. We also compute the error consisting in

Example 1. [9]Let us consider a quartic eigenvalue problem of the form .

We obtain a 144 × 144 quartic pencil, whose 576 eigenvalues are shown in Figure 1 given above.

Example 2. [10]Now, let us consider the following quadratic eigenvalue problems given by.

The 400 eigenvalues are shown in Figure 2 below

Figure 1. Eigenvalues of 144 × 144 polynomial problems.

Figure 2. Eigenvalues of 400 quadratic polynomial problems.

6. Conclusion

We have proposed a numerical approach for solving polynomial eigenvalue problems structured. We first transform polynomial eigenvalue problem to a skew-Hamiltonian/Hamiltonian pencil . The second step is to transform the pencil into a standard Hamiltonian eigenproblem. Numerical methods based on these structured linearizations are expected to be more effective in computing accurate eigenvalues in practical applications. My future work based on this current study is to solve the large matrix equations applied in signal processing, image restoration and model reduction in control theory.

Acknowledgements

We thank the editor and the referee for their comments.

Conflicts of Interest

The author declares no conflicts of interest regarding the publication of this paper.

References

[1]	Bora, S., Karow, M., Mehl, C. and Sharma, P. (2014) Structured Eigenvalue Backward Errors of Matrix Pencils and Polynomials with Hermitian and Related Structures. SIAM Journal on Matrix Analysis and Applications, 35, 453-475. https://doi.org/10.1137/130925621
[2]	Higham, N.J. (2005) Solving Polynomial Eigenproblems by Linearization. School of Mathematics, The University of Manchester, Manchester, M60 1QD.
[3]	Lu, Z.J., van der Vegt, J.J.W. and Xu, Y. (2018) Spectral Approximation for Polynomial Eigenvalue Problems. Computers and Mathematics with Applications, 76, 1184-1197. https://doi.org/10.1016/j.camwa.2018.06.007
[4]	Mehrmann, V. and Watkins, D. (2000) Structure-Preserving Methods for Computing Eigenpairs of Large Sparse Skew-Hamiltonian/Hamiltonian Pencils. SIAM Journal on Scientific Computing, 22, 1905-1925. https://doi.org/10.1137/S1064827500366434
[5]	Perovia, V. and Mackey, D.S. (2018) Linearizations of Matrix Polynomials in Newton Bases. Linear Algebra and Its Applications, 556, 1-45. https://doi.org/10.1016/j.laa.2018.06.030
[6]	Benner, P., Byers, R., Fassbender, H., Mehrmann, V. and Watkins, D. (2000) Cholesky-Like Factorizations of Skew-Symmetric Matrices. Electronic Transactions on Numerical Analysis, 11, 85-93.
[7]	Fassbender, H., Mackey, D.S., Mackey, N. and Xu, H.G. (1998) Hamiltonian Square Roots of Skew-Hamiltonian Matrices. Linear Algebra and Its Applications, 287, 125-159. https://doi.org/10.1016/S0024-3795(98)10137-4
[8]	Mackey, D.S., Mackey, N., Mehl, C. and Mehrmann, V. (2005) Structured Polynomial Eigenvalue Problems: Good Vibrations from Good Linearizations. Technical Report 239, DFG Research Center Matheon, Mathematics for Key Technologies, Berlin.
[9]	Mehrmann, V. and Watkins, D. (2002) Polynomial Eigenvalue Problems with Hamiltonian Structure. Electronic Transactions on Numerical Analysis, 13, 106-118.
[10]	Fassbender, H. and Kressner, D. (2006) Structured Eigenvalue Problems. GAMM-Mitteilungen, 29, 297-318. https://doi.org/10.1002/gamm.201490035