Aunu Integer Sequence as Non-Associative Structure and Their Graph Theoretic Properties

Aminu Alhaji Ibrahim, Sa’idu Isah Abubaka

Sokoto State University, Sokoto, Nigeria.

DOI: 10.4236/apm.2016.66028                

Abstract

The generating function for generating integer sequence of Aunu numbers of prime cardinality was reported earlier by the author in [1]. This paper assigns an operator  on the function  for  where the operation induces addition or subtraction on the pairs of ai, aj elements which are consecutive pairs of elements obtained from a generating set of some finite order. The paper identifies that the set of the generated pairs of integer sequence is non-associative. The paper also presents the graph theoretic applications of the integers generated in which subgraphs are deduced from the main graph and adjacency matrices and incidence matrices constructed. It was also established that some of the subgraphs were found to be regular graphs. The findings in this paper can further be used in coding theory, Boolean algebra and circuit designs.

Keywords

Aunu Numbers, Nonassociative, Graph, Subgraphs, Adjacency Matrix, Incidence Matrix

Received 14 March 2016; accepted 15 May 2016; published 18 May 2016

1. Introduction

An overview of Aunu numbers, Aunu permutations patterns, the 123 and 132 avoiding patterns and their applications was reported by the authors in [2] . This paper considered the prime enumerative function 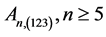generated by the author in [3] and defined an operator on some 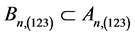using the addition and subtractions as an operators such that the pairing of elements in 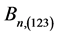was closed in.

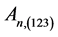In simplest form, a graph is a collection of vertices that can be connected to each other by means of edges. In particular, each edge of graph joins exactly two vertices. Using a formal notation, a graph is defined as follows.

Definition 2.1: A graph G consists of a collection of V vertices and a collection of edges E, for which we write 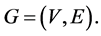Each edge 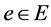is said to join two vertices, which are called its end points. If e joins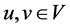, we write 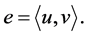Vertex u and v in this case are said to be adjacent. Each e is said to be incident with vertices u and v respectively.

We will often write 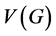and 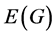to denote the set of vertices and edges associated with graph G respectively. It is important to realize that an edge can actually be represented as an unordered tuple of two vertices, that is, its end points. For this reason, we make no distinction between and: they both represent the fact that vertex u and v are adjacent [4] .

Definition 2.2: A graph H is a subgraph of G if and such that for all with, we have that. When H is a subgroup of G, we write [4] .

Definition 2.3: Adjacency matrix is a table A with n rows and m columns with entry denoting the number of edges joining vertex and [4] .

Definition 2.4: An incidence matrix M of graph G consists of n rows and m columns such that counts the number of times that edge is incident with vertex. Note that is either 0, 1 or 2.

Theorem 2.1: For all graphs G, the sum of the vertex degrees is twice the number of edges [4] . That is,

. (1)

Corollary 2.1: For any graph G, the number of vertices with odd degrees is even [4] .

2. Method of Construction

Let where in this case (being prime numbers). The restriction is deliberately put

since we are only interested in enumerations involving Aunu numbers of (123)-avoiding category which, by definition begins from 5 upwards as reported in [5] . Then;

.

We now obtain from a restricted subset. Then contains all elements of up to 21.

We are now set to carry out some algebraic theoretic investigations on being a direct subset of.

First let us introduce an operator on such that:

Define an operator

(2)

where: is an operator which induces addition or subtraction on any pair whereby addition or subtraction in absolute value is closed in and implies whichever of

Then we obtain from set of pairs

where the superscript p on indicates that is obtained from by breaking elements of into pairs such that application of of (1) on is closed in.

3. Results

3.1. Testing for Nonassociative Properties Using the Stated Pairing Scheme Yields the Following Results

1) Given, we note that: the operation rule is either “+ or −” as earlier defined.

Also

, hence it is not associative.

2)

Also,

, hence it is not associative.

3)

Also,

, hence it is not associative.

4)

Also,

, hence it is not associative.

5)

Also,

, hence it is not associative.

6)

Also,

, hence it is not associative.

7)

Also,

, hence it is not associative

8)

Also,

, hence it is not associative.

9)

Also,

, hence it is not associative.

10)

Also,

, hence it is not associative.

11)

Also,

, hence it is not associative

12)

Also,

, hence it is not associative.

13)

Also,

, hence it is not associative.

3.2. Graph Theoretic Schemes Generated Using Pairs of Elements in A_n and B_n

In what follows some graph theoretic models are presented using pairs of points of and as adjacent nodes.

Figure 6 shows some examples of regular graphs and their adjacency and incidence matrices can be constructed using the same format as outlined in Table 1-10.

Table 1. Adjacency matrix of Figure 1.

Theorem 2.1 and corollary 2.1 has been satisfied. Note also that, every column of incidence matrix has entries 1.

Table 2. Incidence matrix of Figure 1.

Table 3. Adjacency matrix of subgraph in Figure 2.

Theorem 2.1 and corollary 2.1 has been satisfied. Note also that, every column of incidence matrix has entries 1.

Table 4. Incidence matrix of subgraph in Figure 2.

Table 5. Adjacency matrix of subgraph of Figure 3.

Theorem 2.1 and corollary 2.1 has been satisfied. Note also that, every column of incidence matrix has entries 1.

Table 6. Incidence matrix of subgraph of Figure 3.

Table 7. Adjacency matrix of subgraph of Figure 4.

Theorem 2.1 and corollary 2.1 has been satisfied. Note also that, every column of incidence matrix has entries 1.

Table 8. Incidence matrix of subgraph of Figure 4.

Table 9. Adjacency matrix of subgraph of Figure 5.

Theorem 2.1 and corollary 2.1 has been satisfied. Note also that, every column of incidence matrix has entries 1.

Table 10. Incidence matrix of subgraph of Figure 5.

Figure 1. Graph network constructed from elements of A_n and B_n.

Figure 2. Subgraph of the network of Figure 1.

Figure 3. Subgraph of the network of Figure 1.

Figure 4. Subgraph of the network of Figure 1.

Figure 5. Subgraph of the network of Figure 1.

Figure 6. Subgraph of the network of Figure 1.

Figure 7. Subgraph of the network of Figure 1.

Figure 7(i)-(vi) also shows some examples of regular graphs and their adjacency and incidence matrices can be constructed using the same format as outlined in Table 1-10 and can also be viewed as Eulerian circuits.

4. Conclusion

After establishing the non-associativity of the finite sets and under the action of an operator we have also established some good applications in graph network analysis. This, we have achieved by generating some Eulerian circuits which are of some consequences in the study of network theory and in circuits theory. Our results would thus have some promising applications in both the communication and in the signal processing formalisms. Also the results involving adjacency and incidence matrices could be used in communication and coding theory which could be investigated in further researches.

Conflicts of Interest

The authors declare no conflicts of interest.

References

[1]	Sloane, N.J.A. (1964) The On-Line Encyclopedia of Integer Sequences A007619/M4023, A016104, A051021, A079544, A080339.
[2]	Ibrahim, A.A. and Abubakar, S.I. (2016) Non-Associative Property of 123-Avoiding Class of Aunu Permutation Patterns. Advances in Pure Mathematics, 6, 51-57. http://dx.doi.org/10.4236/apm.2016.62006
[3]	Ibrahim, A.A. and Audu, M.S. (2005) Some Group Theoretic Properties of Certain Class of (123) and (132) Avoiding Patterns of Certain Numbers: An Enumeration Scheme. African Journal of Natural Science, 8, 79-84.
[4]	Van Steen, M. (2010) An Introduction to Graph Theory and Complex Networks. Amsterdam
[5]	Ibrahim, A.A. (2006) Some Graph Theoretical Properties of (132)-Avoiding Patterns of Certain Class of Aunu Numbers. Nigerian Journal of Renewable Energy, 14, 21-24.