Asymptotic Stability of Solutions of Lotka-Volterra Predator-Prey Model for Four Species

A. A. Soliman^1*, E. S. Al-Jarallah²

¹Department of Mathematics, Faculty of Sciences, Benha University, Benha, Egypt.
²Department of Mathematics, Faculty of Education, Al Jouf University, Al-Jawf, Kingdom of Saudi Arabia.

DOI: 10.4236/am.2015.64063                

Abstract

In this paper, we consider Lotka-Volterra predator-prey model between one and three species. Two cases are distinguished. The first is Lotka-Volterra model of one prey-three predators and the second is Lotka-Volterra model of one predator-three preys. The existence conditions of nonnega-tive equilibrium points are established. The local stability analysis of the system is carried out.

Keywords

Lotka-Volterra, Prey-Predators, Species, Equilibrium Points Stability, Locally Asymptotically Stable, Globally Asymptotically Stable, Unstable

1. Introduction

The Lotka-Volterra model provides a nice mathematical device to study and understand complex systems of mutually interacting species or agent [1] . In the past decades, Lotka-Volterra type systems have been extensively investigated, especially in biology and ecology [2] -[8] . A basic issue addressed in the studies concerns stability property of the systems because of its relevance to the coexistence of different species in a community [9] . It turns out that the stability of a Lotka-Volterra system relies crucially on the interaction matrix of the system.

A Lotka-Volterra system of n-dimensions is expressed by the ordinary differential equations [4] [10] :

(1.1)

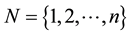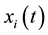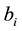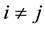where and n is the species number. In (1.1), the function represents the density of species i at time t, the constant, is the carrying capacity of species i, and represents the effect of interspecific (if) or intraspecific (if) interaction. In vector form, System (1.1) is expressed as

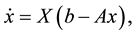
where is an n-dimensional state vector, is an 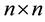diagonal matrix, 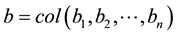is an n-dimensional real vector, and 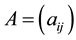is an 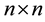community matrix.

The existence and stability of a nonnegative equilibrium point of system (1.1) or subsystems of (1.1) has been investigated by many authors [9] [11] and [12] . The global stability of system (1.1) has been studied by many authors [9] [11] [13] -[16] .

In this paper, we shall concentrate on Lotka-Volterra systems of the fourth dimension. A Lotka-Volterra two preys-two predators system is studied by Takeuchi and Adachi [15] , and [16] . The first is Lotka-Volterra model of one prey-three predators and the second is Lotka-Volterra model of three prey-one predator.

This work is organized as follows: In Section 2, we describe our model. In Section 3, the existence conditions of nonnegative equilibrium points are established. The local stability analysis of the system is carried out in Section 4.

In Section 5, we present an example to clarify each case.

2. The Model

Lotka-Volterra Model

In this section we consider Lotka-Volterra predator-prey model between one and three species and assume that there is no interspicific competition between the three species x₂, x₃ and x₄. This is represented by the following system of differential equations:

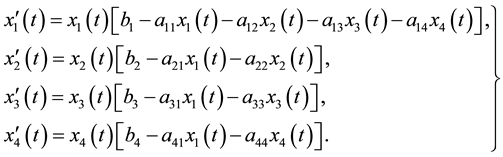(2.1)

where represents the density of species i at time t, the constant is the carrying capacity of species i and represents the effect of interspecific (if) or intraspecific (if) interaction. In vector form, system (2.1) is expressed as:

where is a 4-dimensional state vector, is a 4 × 4 diagonal matrix, is a 4-dimnsional real vector, and

(2.2)

is a 4 × 4 community matrix.

The system (2.1) is a prey-predator system if the following assumption is satisfied.

(H1)

Two cases of system (2.1) can be distinguished:

The first case describes a one prey-three predators system where x₁ represents the prey and x₂, x₃, x₄ represent the predators. In this case we assume that the following conditions are satisfied in addition to (H1):

(H2)

(H3)

The second case describes a one predator-three preys system where x₁ represents the predator and x₂, x₃, x₄ represent the preys. In this case we assume that the following conditions are satisfied in addition to (H1).

(H2)'

(H3)'

3. Equilibrium Analysis

3.1. Existence of the Quilibrium Points

In this section, the existence of the equilibrium points of system (2.1) in each case is investigated. At most there are nine possible non-negative equilibrium points for system (2.1) in the first case, the existence conditions of them are given as the following:

1) The equilibrium points and are always exist where E₁ is the equilibrium point in the absence of predation and according to conditions (H1) and (H3).

2) The positive equilibrium point exists in the first quadrant of the plane if and only if the following condition is satisfied

(H4):

where and are given by

(3.1)

3) The positive equilibrium point exists in the first octant of space if and only if the following conditions are satisfied:

(H5):

where and are given by

(3.2)

4) The positive equilibrium point exists in the positive cone (nonnegative octant)

if and only if the following conditions are satisfied

(H6)

where are given by

(3.3)

where

A is the interaction matrix defined in (2.2).

For the second case of system (2.1), at most there are fifteen possible nonnegative equilibrium points. The existence conditions of them are given as the following:

1) The equilibrium points

, , and

are always exist where E₂, E₃, E₄ are the equilibrium points in the absence of predation and according to conditions (H1) and (H3)'.

2) The positive equilibrium point exists in the first quadrant of plane if and only if the following condition is satisfied

(H4)':

where and are given by (3.1).

3) In the absence of predator and one prey species, both the other two prey species grow. Thus, the equilibrium point always exists in the interior of plane where, according to conditions (H1) and (H3)'.

4) The positive equilibrium point exists in the first octant of space if and only if the following conditions are satisfied

(H5)'

where, and are given by (3.2).

5) In the absence of predator, all three prey species grow. Thus, the positive equilibrium point

always exists in the interior of space.

6) The positive equilibrium point exists in if and only if the following conditions are satisfied

(H6)':

where are given by (3.3).

3.2. Remark

We will use the symbols, and to denote the nonnegative equilibrium points, and respectively, where and are given by (3.1), the symbols, and to denote the nonnegative equilibrium points, and respectively, where are given by (3.2) and use the symbols

, and to denote the nonnegative equilibrium points, and respectively.

4. Stability Analysis

4.1. Stability of Equilibrium Points

In this section, the local stability analysis of equilibrium points is investigated. Assuming that all previous equilibrium points existing.

The Jacobian matrix J of system (2.1) is given by:

(4.1)

Computing the variation matrixes corresponding to each equilibrium point and then using Routh-Hurwitz criteria [17] , the following results can be observed:

1) Substituting by E₀ in the variation matrix (4.1), we get the eigenvalues

So for the first case, E₀ is a saddle point with locally stable manifold in the x₂x₃x₄ space and with unstable manifold in the x₁ direction. Near E₀ the prey’s population x₁ grows while the predators’ populations x₂, x₃ and x₄ decline.

For the second case, E₀ is a saddle point with locally stable manifold in the x₁ direction and with unstable manifold in the x₂x₃x₄ space. Near E₀ the predator population x₁ decline while the preys’ populations x₂, x₃ and x₄ grow.

2) Substituting by E₁ in the variation matrix (4.1), we get the eigenvalues, ,

.

(By using (H3) and (H4)).

So E₁ is a saddle point with locally stable manifold in the x₁ direction and with unstable manifold in the x₂x₃x₄ space. Near E₁ the prey species x₁ remains close to.

Similarly, E₂ has three positive eigenvalues

(By using (H3)' and (H4)')

So E₂ is a saddle point with locally stable manifold in the x₂ direction and with unstable manifold in the x₁x₃x₄ space. Near E₂ the prey species x₂ remains close to.

E₃ and E₄ have the same stability behavior of E₂.

We now state the local stability behavior of other equilibrium points in the form of Theorems. The proofs of these theorems follow directly from the Routh-Hurwitz criteria [12] .

Theorem 4.1

1) E₁₂ is locally asymptotically stable in the x₁x₂ plane.

2) If E₁₂₃₀ and E₁₂₀₄ exist, then E₁₂₀₀ is a saddle point with locally stable manifold in the x₁x₂ plane and with unstable manifold in the x₃x₄ plane.

Proof

Consider the following subsystem from (2.1)

(4.2)

Evaluating the variation matrix of system (4.2) at E₁₂, we have

The characteristic polynomial is

(4.3)

Since

Then, and have negative real parts. Thus, E₁₂ is locally asymptotically stable in the x₁x₂ plane.

Computing the variation matrix (4.1) at E₁₂₀₀, we have

The characteristic equation of matrix V₁₂ is

Comparing with (4.3) we get that and have negative real parts and

If E₁₂₃₀ and E₁₂₀₄ exist, then and (by using (H5) and (H5)').

Therefore, E₁₂₀₀ is a saddle point with locally stable manifold in the x₁x₂ plane and with unstable manifold in the x₃x₄ plane.

4.2. Remark

1) Behavior of solutions near the equilibrium points E₁₃ and E₁₄ are the same behavior of solutions near the equilibrium point E₁₂.

2) Behavior of solutions near E₁₀₃₀ and E₁₀₀₄ are the same behavior of solutions near E₁₂₀₀.

Theorem 4.1

a) E₂₃ is locally asymptotically stable in the x₂x₃ plane.

b) If E₁₂₃₀ exists, then E₀₂₃₀ is a saddle point with locally stable manifold in the x₂x₃ plane and with unstable manifold in the x₁x₄ plane.

Proof

Consider the following subsystem from (2.1)

(4.4)

Evaluating the variation matrix of system (4.4) at E₂₃, we have

which have the eigenvalues and (by using (H3)').

Therefore, E₂₃ is locally asymptotically stable in the x₂x₃ plane.

Substituting by E₀₂₃₀ in the variation matrix (4.1), we get the eigenvalues

If E₁₂₃₀ exists, then

(By using (H3)' and (H5)').

Hence E₀₂₃₀ is a saddle point with locally stable manifold in the x₂x₃ plane and with unstable manifold in the x₁x₄ plane.

Theorem 4.2

a) E₁₂₃ is locally asymptotically stable in the x₁x₂x₃ space.

b) If exists, then E₁₂₃₀ is a saddle point with locally stable manifold in the x₁x₂x₃ space and with unstable manifold in the x₄ direction.

Proof

Consider the following subsystem from (2.1)

(4.5)

Evaluating the variation matrix of system (4.5) at E₁₂₃, we have

which has the characteristic polynomial

(4.6)

where

From Routh-Hurwitz criterion, E₁₂₃ is locally asymptotically stable if and only if, and.

It is clear that all the coefficients c₁, c₂ and c₃ are positive and

Therefore E₁₂₃ is locally asymptotically stable in the x₁x₂x₃ space.

Substituting by E₁₂₃₀ in the variation matrix (4.1), we get the characteristic equation

Comparing with (4.6), we obtain that, and have negative real parts while (by using (H6) and (H6)')

Therefore, E₁₂₃₀ is a saddle point with locally stable manifold in the x₁x₂x₃ space and with unstable manifold in the x₄ direction.

Remark 4.1

1) Behavior of solutions near E₁₂₄ and E₁₃₄ are the same behavior of solutions near the equilibrium point E₁₂₃.

2) Behavior of solutions near E₁₂₀₄ and E₁₀₃₄ are the same behavior of solutions near E₁₂₃₀.

Theorem 4.3

a) E₂₃₄ is locally asymptotically stable in the x₂x₃x₄ space.

b) If exists, then E₀₂₃₄ is a saddle point with locally stable manifold in the x₂x₃x₄ space and with unstable manifold in the x₄ direction.

Proof

Proof of this theorem follows directly as proof of Theorem 4.2

Now, we study asymptotic stability of the positive equilibrium.

Substituting by in the variation matrix (4.1), we get the characteristic equation

where

From Routh-Hurwitz criterion [12] , is locally asymptotically stable if and only if and.

It is clear that all the coefficients c₁, c₂, c₃ and c₃ are positive and if

Then is locally asymptotically stable in.

Theorem 4.4

is globally asymptotically stable in for every carrying capacity.

Proof.

We define the Liapunov function by

where,

In the region

It is clear that

Then calculating the time derivative of V along the positive solutions of system (2.1), we have

Then, we can choose

Hence, we obtain

Therefore, it follows from well-known Liapunov-LaSalle theorem that the positive equilibrium is globally asymptotically stable in.

5. Numerical Simulations

The reader can be check local asymptotic stability of the system 2.1 for:

Example 5.1

Example 5.2

Acknowledgements

The authors would like to thank all staff members who help me in this article.

NOTES

^*Corresponding author.

Conflicts of Interest

The authors declare no conflicts of interest.

References

[1]	May, R.M. (1973) Stability and Complexity in Model Ecosystems. Princeton University Press, Princeton.
[2]	Edelstein-Keshet, L. (2005) Mathematical Models in Biology. Society for Industrial and Applied Mathematics, New York. http://dx.doi.org/10.1137/1.9780898719147
[3]	Farkas, M. Dynamical Models in Biology. Elsevier Science and Technology Books, 200.
[4]	Freedman, H.I. (1980) Deterministic Mathematical Models in Population Ecology. Marcel Dekker, Inc., New York.
[5]	Murray, J.D. (2002) Mathematical Biology, Interdisciplinary Applied Mathematics. Springer, Berlin.
[6]	Perthame, B. (2007) Transport Equations in Biology. Birkh?user Verlag, Basel.
[7]	Solimano, F. and Berettra, E. (1982) Graph Theoretical Criteria for Stability and Boundedness of Predator-Prey System. Bulletin of Mathematical Biology, 44, 579-585. http://dx.doi.org/10.1137/1.9780898719147
[8]	Takeuchi, Y., Adachi, N. and Tokumaru, H. (1978) The Stability of Generalized Volterra Equations. Journal of Mathe-matical Analysis and Applications, 62, 453-473. http://dx.doi.org/10.1016/0022-247X(78)90139-7
[9]	Ji, X.-H. (1996) The Existence of Globally Stable Equilibria of N-Dimensional Lotka-Volterra Systems. Applicable Analysis: An International Journal, 62, 11-28. http://dx.doi.org/10.1080/00036819608840467
[10]	Arrowsmith, D.K. and Place, C.M. (1982) Ordinary Differential Equation. Chapman and Hall, New York.
[11]	Li, X.-H., Tang, C.-L and Ji, X.-H. (1999) The Criteria for Globally Stable Equilibrium in N-Dimensional Lotka-Vol-terra Systems. Journal of Mathematical Analysis and Applications, 240, 600-606. http://dx.doi.org/10.1006/jmaa.1999.6612
[12]	Lu, Z. (1998) Global Stability for a Lotka-Volterra System with a Weakly Diagonally Dominant Matrix. Applied Ma-thematics Letters, 11, 81-84. http://dx.doi.org/10.1016/S0893-9659(98)00015-9
[13]	Liu, J. (2003) A First Course in the Qualitative Theory of Differential Equations. Person Education, Inc., New York.
[14]	Takeuchi, Y. and Adachi, N. (1980) The Existence of Globally Stable Equilibria of Ecosystems of the Generalized Volterratyp. Journal of Mathematical Biology, 10, 401-415. http://dx.doi.org/10.1007/BF00276098
[15]	Takeuchi, Y. Adachi, N. (1984) Influence of Predation on Species Coexistence in Volterra Models. Journal of Mathe-matical Biology, 70, 65-90. http://dx.doi.org/10.1016/0025-5564(84)90047-6
[16]	Takeuchi, Y. (1996) Global Dynamical Properties of Lotka-Volterra Systems. World Scientific, Singapore City. http://dx.doi.org/10.1142/9789812830548
[17]	Rao, M. (1980) Ordinary Differential Equations Theory and Applications. Pitman Press, Bath.