Domination in Controlled and Observed Distributed Parameter Systems ()
1. Introduction
This work concerns the systems analysis and more precisely a general concept of domination. This notion consists to study the possibility of comparison or classification of systems. It was introduced firstly in [1] for controlled and observed lumped systems and then in [2] for a class of distributed parameter systems. The developed approach concerns separately the input and output operators. Various results are given and illustrated by applications and examples. A duality between the two cases is established. An extension of [2] to the regional case is given in [3]. The regional aspect of this problem is motivated by the fact that a system may dominates another one in a region , but not on the whole geometrical support
, but not on the whole geometrical support  of the system.
of the system.
Let us note that in the case of the dual notions of observability and controllability, the literature is very rich. However, the purpose is different and generally, the main problem is how to reconstruct the state of the considered system or to reach a desired state, i.e. to study if a system is (or not) observable or controllable.
In this paper, we consider and we study a more general domination problem in the case of a class of controlled and observed systems [4-6]. The developed approach depends on the different parameters of the considered systems, such their dynamics, their input and output operators. Indeed, we consider without loss of generality, a class of linear distributed systems as follows
 (1)
(1)
where  generates a strongly continuous semi-group
generates a strongly continuous semi-group
(s.c.s.g.)  on the state
on the state .
. ,
,

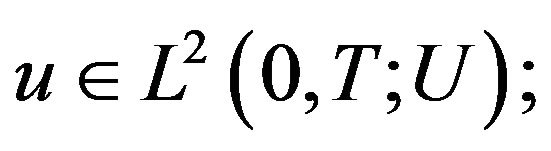 and
and  are respectively the state and the control spaces, assumed to be Hilbert spaces. The system (1) is augmented with the following output equation
are respectively the state and the control spaces, assumed to be Hilbert spaces. The system (1) is augmented with the following output equation
 (2)
(2)
with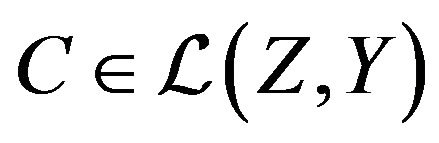 ,
,  is the observation space, a Hilbert space. The operator
is the observation space, a Hilbert space. The operator  is the dynamics of the system, the operators
is the dynamics of the system, the operators  and
and 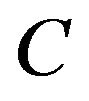 are respectively the input and output operators. The state
are respectively the input and output operators. The state  of the system at time
of the system at time  is given by
is given by
 (3)
(3)
where
 (4)
(4)
and the observation by
 (5)
(5)
The first problem consists to study a possible comparison of controlled systems as system (1), with respect to an output operator . We give the main properties and characterization results. The case of sensors and actuators is also examined. Illustrative examples and applications are presented and various other situations are examined.
. We give the main properties and characterization results. The case of sensors and actuators is also examined. Illustrative examples and applications are presented and various other situations are examined.
Then, an analogous study concerning the domination of observed systems, with respect to an input operator , is given. Finally, we study the relationship between the notion of domination and the compensation problem [7,8].
, is given. Finally, we study the relationship between the notion of domination and the compensation problem [7,8].
2. Domination for Controlled Systems
2.1. Problem Statement and Definitions
We consider the following linear distributed systems
 (6)
(6)
 (7)
(7)
where, for ;
;  is a linear operator generating a s.c.s.g.
is a linear operator generating a s.c.s.g.  on the state space
on the state space .
.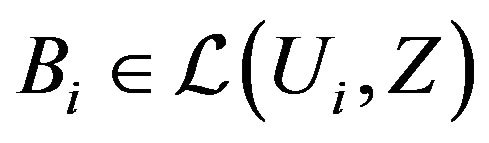 ,
,
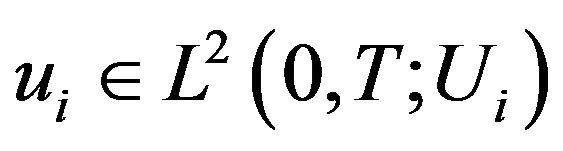 ;
;  is a control space. The systems
is a control space. The systems  and
and  are respectively augmented with the output equations
are respectively augmented with the output equations
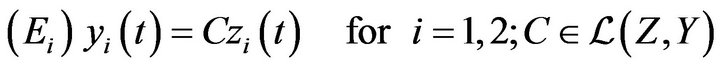
The state of  at the final time
at the final time  is given by
is given by
 (8)
(8)
where
 (9)
(9)
The corresponding observation at time  is given by
is given by
 (10)
(10)
The purpose is to study a possible comparison of systems  and
and  (or the input operators
(or the input operators  and
and  if
if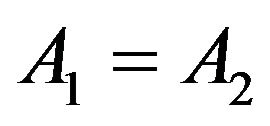 ) with respect to the output operator
) with respect to the output operator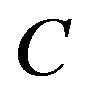 .
.
It is based on the dynamics  and
and , the control operators
, the control operators ,
, 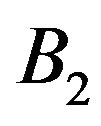 and the observation operator
and the observation operator . Without loss of generality, one can assume that
. Without loss of generality, one can assume that 
 . We introduce hereafter the corresponding notion of domination.
. We introduce hereafter the corresponding notion of domination.
Definition 1. We say that
1)  dominates
dominates  (or the pair
(or the pair  dominates
dominates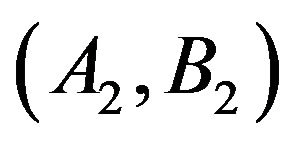 ) exactly on
) exactly on  with respect to the operator
with respect to the operator , if
, if

2)  dominates
dominates  (or the pair
(or the pair 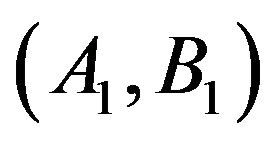 dominates
dominates ) weakly on
) weakly on , with respect to the operator
, with respect to the operator , if
, if
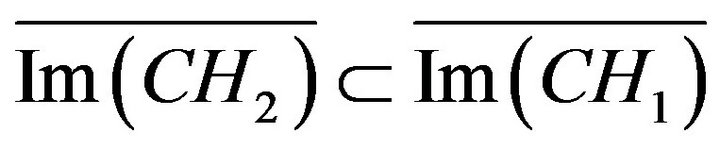
In this situation, we note respectively

Let us give following properties and remarks :
1) Obviously, the exact domination with respect to an output operator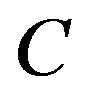 , implies the weak one with respect to
, implies the weak one with respect to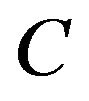 . The converse is not true, this is shown in [2] for
. The converse is not true, this is shown in [2] for  and
and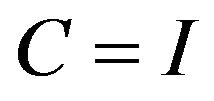 ).
).
2) If the system 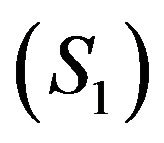 is controllable exactly (respectively weakly), or equivalently
is controllable exactly (respectively weakly), or equivalently

then  dominates exactly (respectively weakly) any system
dominates exactly (respectively weakly) any system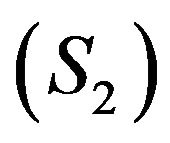 , with respect to any output operator
, with respect to any output operator .
.
3) In the case where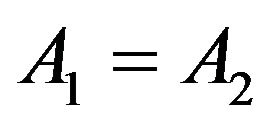 ,
, 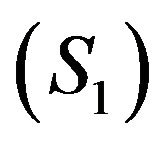 dominates
dominates  exactly (respectively weakly), we say simply that
exactly (respectively weakly), we say simply that  dominates
dominates 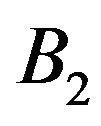 exactly (respectively weakly). Then, we note
exactly (respectively weakly). Then, we note

Hence, one can consider a single system with two inputs as follows
 (11)
(11)
augmented with an output equation

In this case, the domination of control operators  and
and  with respect to the observation operator
with respect to the observation operator  is similar. The definitions and results remain practically the same.
is similar. The definitions and results remain practically the same.
4) The exact or weak domination of systems (or operators) is a transitive and reflexive relation, but it is not antisymmetric. Thus, for example in the case where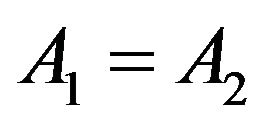 , for any non-zero operator
, for any non-zero operator  and
and , we have1
, we have1 , even if
, even if  for
for .
.
5) Concerning the relationship with the notion of remediability [7,8], we consider without loss of generality, a class of linear distributed systems described by the following state equation
 (12)
(12)
where  is a known or unknown disturbance. The system (12) is augmented with the following output equation
is a known or unknown disturbance. The system (12) is augmented with the following output equation
 (13)
(13)
The state  of the system at time
of the system at time  is given by
is given by

where

If the system (12), augmented with (13), is exactly (respectively weakly) remediable on , or equivalently
, or equivalently 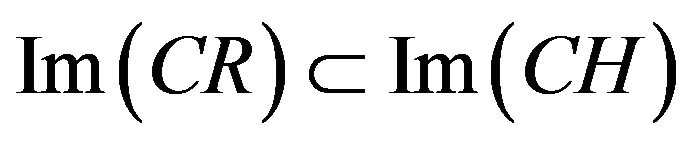 (respectively
(respectively 
 ), then
), then  dominates any operator
dominates any operator  exactly (respectively weakly) with respect to the operator
exactly (respectively weakly) with respect to the operator .
.
6) For 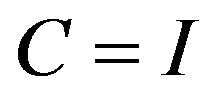 and
and , one retrieve the particular notion of domination as in [2].
, one retrieve the particular notion of domination as in [2].
We give hereafter characterization results concerning the exact and weak domination.
2.2. Characterizations
The following result gives a characterization of the exact domination with respect to the output operator .
.
Proposition 2. The following properties are equivalent 1) The system 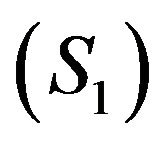 dominates exactly
dominates exactly  with respect to the operator
with respect to the operator .
.
2) For any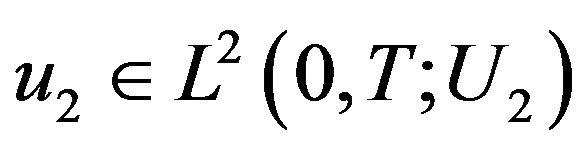 , there exists
, there exists 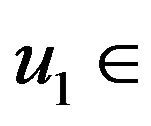
 such that
such that
 (14)
(14)
3) There exists  such that for any
such that for any , we have
, we have
 (15)
(15)
Proof.
The equivalence between i) and ii) derives from the definition.
The equivalence between ii) and iii) is a consequence of the fact that if  and
and  are Banach spaces;
are Banach spaces;  and
and  then
then

if and only if, there exists 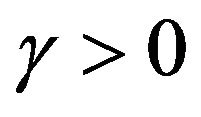 such that for any
such that for any , we have
, we have
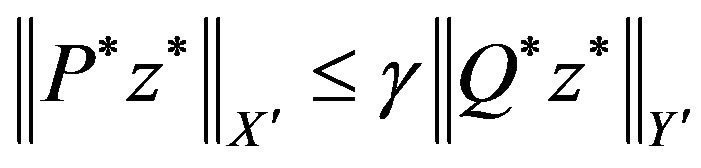
where ,
,  and
and  are respectively the dual spaces of
are respectively the dual spaces of ,
,  and
and .
.
Concerning the weak case, we have the following characterization result.
Proposition 3.
The system  dominates
dominates  weakly, with respect to
weakly, with respect to , if and only if
, if and only if
 (16)
(16)
Proof.
Derives from the definition and the fact that  is equivalent to
is equivalent to 
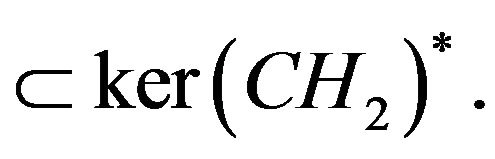
It is well known that the choice of the input operator play an important role in the controllability of a system [4-6,9-11]. Here also, the domination for controlled systems, with respect to an output operator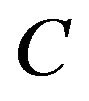 , depends on the dynamics
, depends on the dynamics  and particularly on the choice of the control operators
and particularly on the choice of the control operators . However, even if
. However, even if 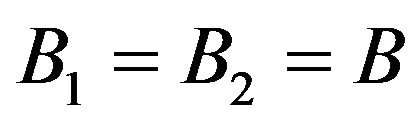 (with the same actuator), the pair
(with the same actuator), the pair  may dominates
may dominates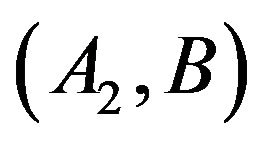 . This is illustrated in the the following example.
. This is illustrated in the the following example.
Example 4. We consider the system described by the one dimension equation

The operator  generates the s.c.s.g.
generates the s.c.s.g.  defined by
defined by

where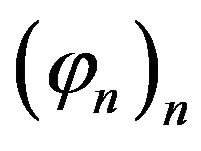 , with
, with , is a complete system of eigenfunctions of
, is a complete system of eigenfunctions of 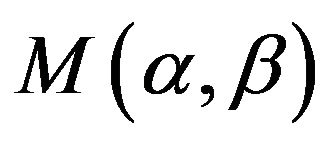 associated to the eigenvalues
associated to the eigenvalues 
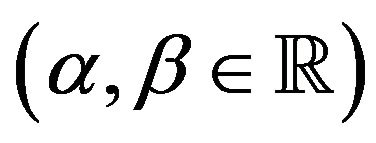 .
.
For , we have
, we have
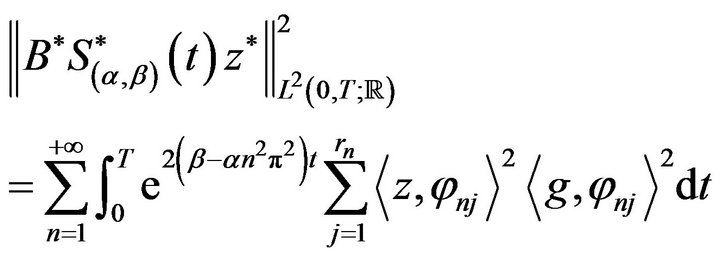 (17)
(17)
Hence, if 
 Equation (17) becomes
Equation (17) becomes

Let  and
and 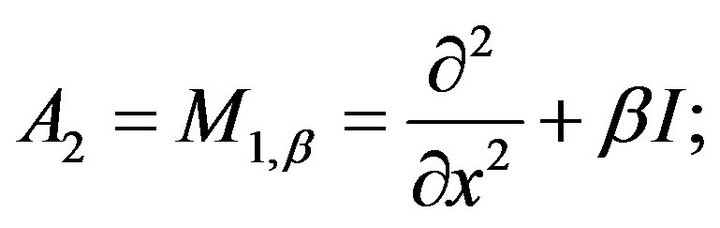
 .
.
The corresponding semi-groups, noted  and
and , are respectively defined by
, are respectively defined by
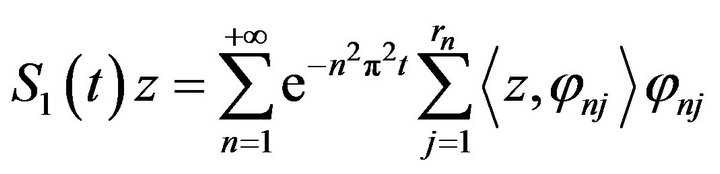
and

Then for 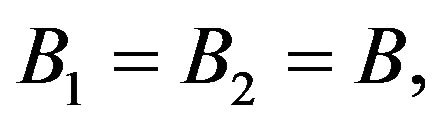 with
with 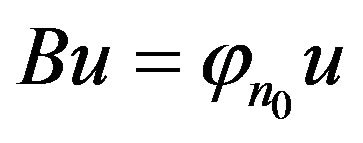
1) If  then for any
then for any , we have
, we have

consequently, the pair  dominates the pair
dominates the pair  exactly, and hence weakly.
exactly, and hence weakly.
2) If 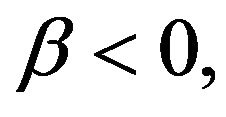 then for any
then for any ,
,
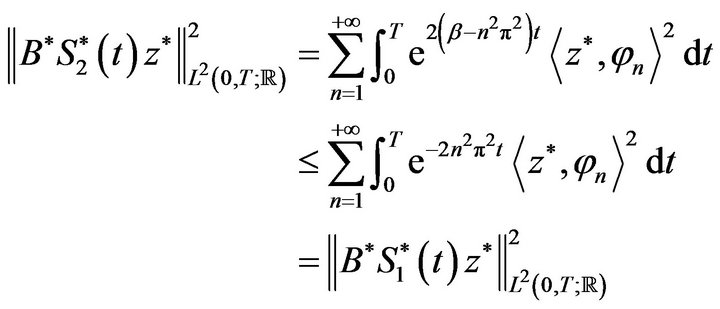
Hence, the pair  dominates the pair
dominates the pair  exactly (and weakly).
exactly (and weakly).
In the next section, we examine the case of a finite number of actuators, and then the case where the observation is given by sensors.
2.3. Case of Actuators and Sensors
This section is focused on the notions of actuators and sensors [4,8,10], i.e. on input and output operators. In what follows, we assume that  and, without loss of generality, we consider the analytic case where
and, without loss of generality, we consider the analytic case where 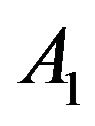 and
and  generate respectively the s.c.s.g.
generate respectively the s.c.s.g.  and
and 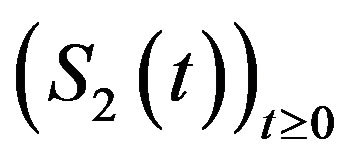 defined by
defined by
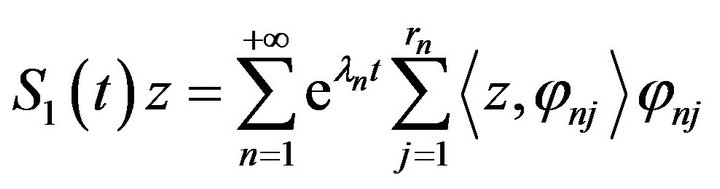 (18)
(18)
and
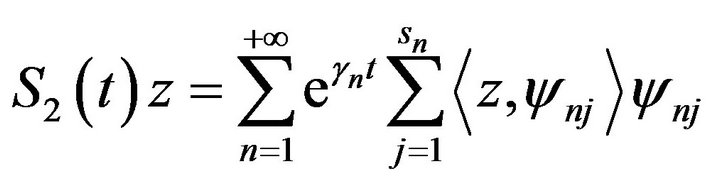 (19)
(19)
where  is a complete orthonormal basis of eigenfunctions of
is a complete orthonormal basis of eigenfunctions of , associated to the real eigenvalues
, associated to the real eigenvalues  such that
such that ;
;  is the multiplicity of
is the multiplicity of .
.
 is a complete orthonormal basis of eigenfunctions of
is a complete orthonormal basis of eigenfunctions of , associated to the real eigenvalues
, associated to the real eigenvalues  such that
such that ;
;  is the multiplicity of
is the multiplicity of .
.
2.3.1. Case of Actuators
In the case where  is excited by
is excited by  zone actuators
zone actuators  , we have
, we have  and
and
 (20)
(20)
where  and
and ;
;
 . We have
. We have
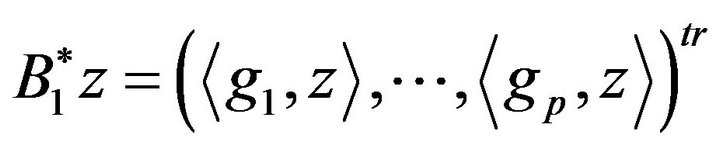 (21)
(21)
By the same, if  is excited by
is excited by  zone actuators
zone actuators , we have
, we have  and
and
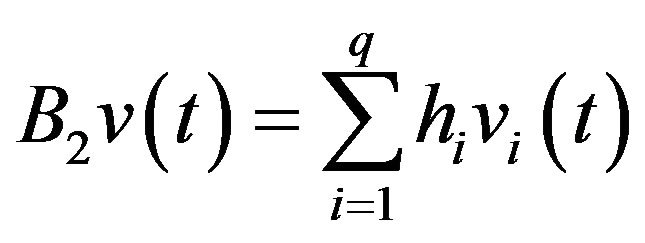 (22)
(22)
with ,
,  ,
,
 and
and
 (23)
(23)
As it will be seen in the next section, this leads to characterization results depending on  and the corresponding controllability matrix, and then on the observability one in the case where the observation is given by a finite number of sensors. First, let us show the following preliminary result.
and the corresponding controllability matrix, and then on the observability one in the case where the observation is given by a finite number of sensors. First, let us show the following preliminary result.
Proposition 5. We have

and
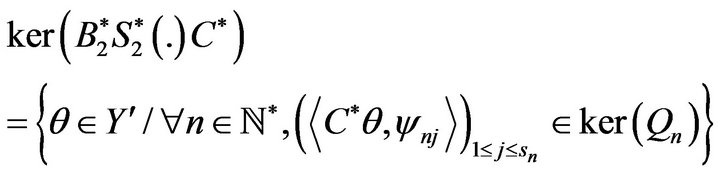
where  and
and  are the corresponding controllability matrices defined by
are the corresponding controllability matrices defined by

and
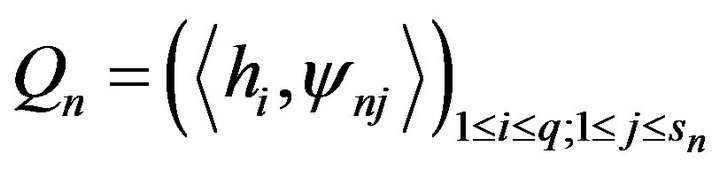
Proof. We have

Therefore,  if and only if
if and only if

By analyticity, this is equivalent to

or

where

The proof of the second equality of the proposition is similar.
The following result deriving from proposition 2, gives characterizations of exact and weak domination in the case of actuators.
Proposition 6.
1)  dominates
dominates 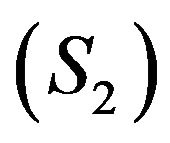 exactly with respect to the operator
exactly with respect to the operator  if and only if there exists
if and only if there exists  such that for any
such that for any , we have
, we have

2)  dominates
dominates  weakly with respect to the operator
weakly with respect to the operator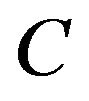 , if and only if for any
, if and only if for any , we have
, we have

Let us note that if , the domination concerns the operators
, the domination concerns the operators 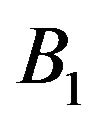 and
and , and then the corresponding actuators. This leads to the following definition.
, and then the corresponding actuators. This leads to the following definition.
Definition 7. If  dominates
dominates  exactly (respectively weakly) with respect to the operator
exactly (respectively weakly) with respect to the operator , we say that
, we say that  dominate
dominate 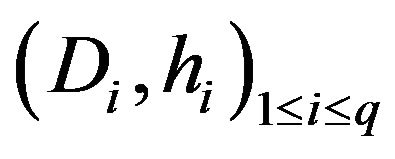 exactly (respectively weakly) with respect to
exactly (respectively weakly) with respect to .
.
In the usual case, the observation is given by sensors. This is examined in following section.
2.3.2. Case of Sensors
Now, if the output is given by  sensors
sensors , we have
, we have

and
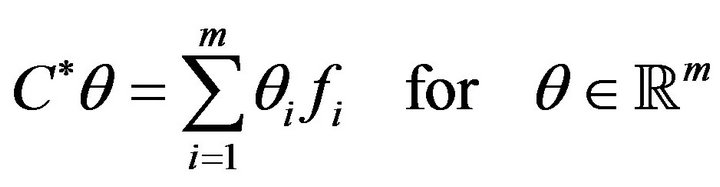
We have the following proposition.
Proposition 8. 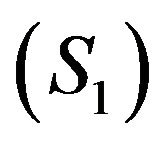 dominates
dominates  weakly with respect to the sensors
weakly with respect to the sensors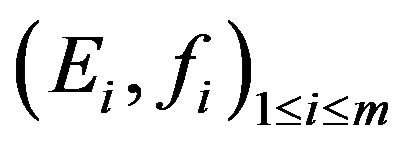 , if and only if
, if and only if
 (24)
(24)
where  and
and  are the corresponding observability matrices defined by
are the corresponding observability matrices defined by
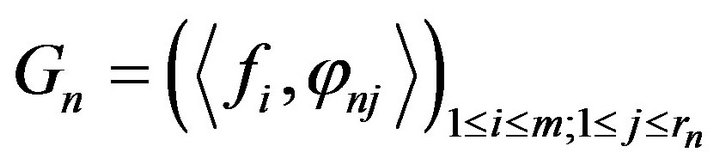
and

Proof.  dominates
dominates 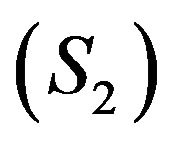 weakly with respect to the sensors
weakly with respect to the sensors , if and only if, for any
, if and only if, for any ,
,
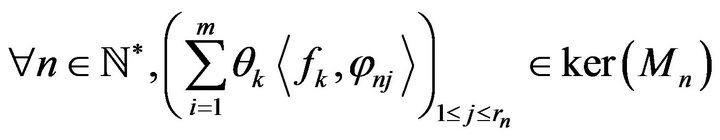
implies that
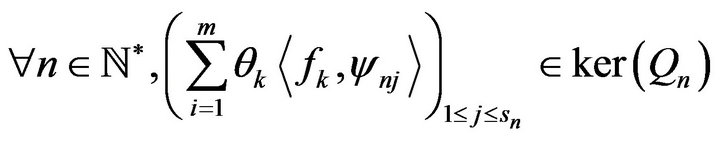
or equivalently, for any ,
,

we then have the result.
Let us give the following remarks.
1) If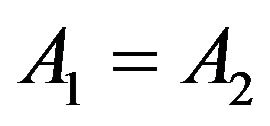 , we have
, we have , for
, for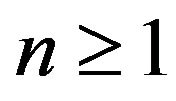 .
.
2) One actuator may dominates 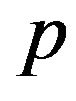 actuators
actuators , with respect to an output operator
, with respect to an output operator  (sensors).
(sensors).
3) In the case of one actuator and one sensor, i.e. for 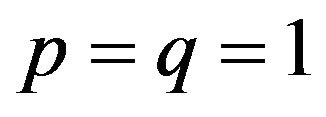 and
and  we have
we have

and

Then
 (25)
(25)
4) In the case of a finite number of sensors, the exact and weak domination are equivalent.
3. Application to Diffusion Systems
To illustrate previous results and other specific situations, we consider without loss of generality, a class of diffusion systems described by the following parabolic equation.
 (26)
(26)
where  is a bounded subset of
is a bounded subset of  with a sufficiently regular boundary
with a sufficiently regular boundary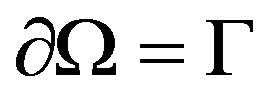 ;
;  and
and  for
for 
 is augmented with the output equation
is augmented with the output equation
 (27)
(27)
We examine respectively, hereafter the case of one and two space dimension.
3.1. One Dimension Case
In this section, we consider the systems  and
and  described by the following one dimension equations, with
described by the following one dimension equations, with  and
and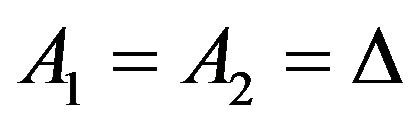 .
.
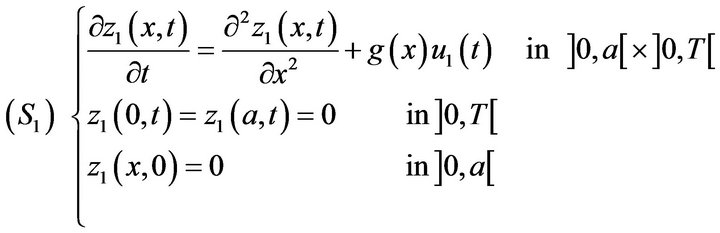 (28)
(28)
 (29)
(29)
 admits a complete orthonormal system of eigenfunctions
admits a complete orthonormal system of eigenfunctions  associated to the eigenvalues
associated to the eigenvalues
 with
with 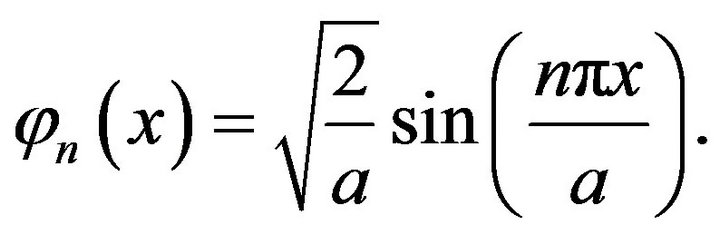
Each system  is augmented with the output equation corresponding to a sensor
is augmented with the output equation corresponding to a sensor ,
,
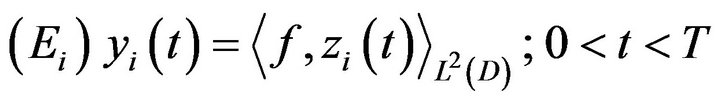 (30)
(30)
According to proposition 8,  dominates
dominates  with respect to the sensor
with respect to the sensor , if and only if,
, if and only if,
 (31)
(31)
Let  such that
such that  We suppose that
We suppose that  and
and  are respectively excited by the actuators
are respectively excited by the actuators  and
and , i.e.
, i.e. 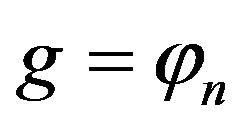 and
and .
.
Then
•  dominates
dominates 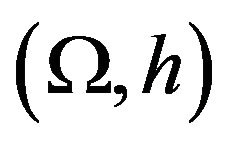 with respect to the sensor
with respect to the sensor  and
and
• 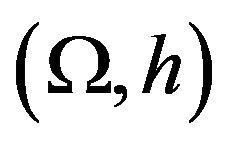 dominates
dominates 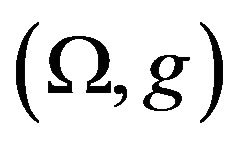 with respect to the sensor
with respect to the sensor 
Let us also note that in the one dimension case, any operators  and
and  are comparable. this is not always possible in the two-dimension case which will be examined in the next section.
are comparable. this is not always possible in the two-dimension case which will be examined in the next section.
3.2. Two Dimension Case
Now, we consider the case where  and the systems described by the following equations
and the systems described by the following equations

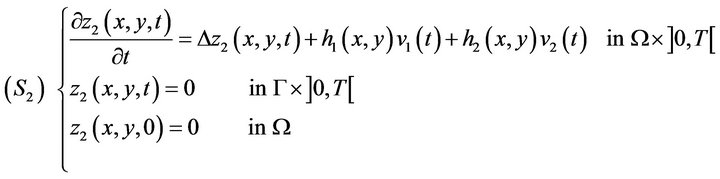
Here, we have  and
and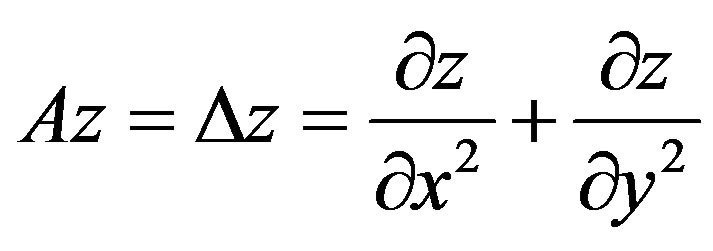 for
for 
 admits a complete orthonormal system of eigenfunctions
admits a complete orthonormal system of eigenfunctions 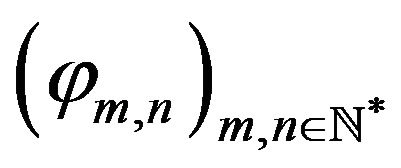 associated to the eigenvalues
associated to the eigenvalues  defined by
defined by
 (32)
(32)
 and
and  are respectively augmented with the output equations
are respectively augmented with the output equations

and

Let us first note that: , then
, then  is a double eigenvalue, corresponding to the eigenfunctions
is a double eigenvalue, corresponding to the eigenfunctions  and
and 
By the same,  , then
, then 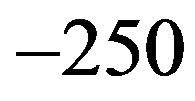 is also a double eigenvalue, corresponding to the eigenfunctions
is also a double eigenvalue, corresponding to the eigenfunctions  and
and 
The examples given hereafter show the following situations :
• An actuator may dominates another one with respect to a sensor.
• None of the systems does not dominates the other.
Example 9. In the case where ,
,
 ,
,  and
and  we have
we have
 (33)
(33)
where  denotes the y-axis. Therefore
denotes the y-axis. Therefore  dominates
dominates 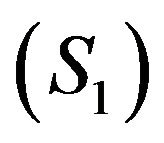 with respect to the corresponding output operator
with respect to the corresponding output operator 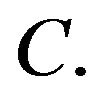
On the other hand, for ,
, 
 and
and  we have
we have
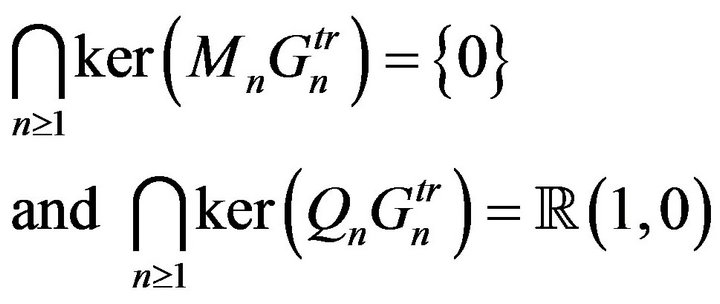 (34)
(34)
where 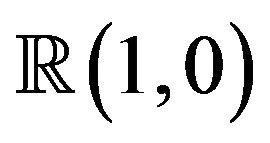 denotes the x-axis. Then
denotes the x-axis. Then 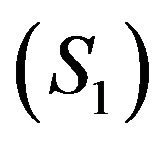 dominates
dominates  with respect to the corresponding output operator
with respect to the corresponding output operator 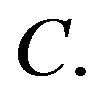
Example 10. Now, for ,
, 
 ,
,  and
and 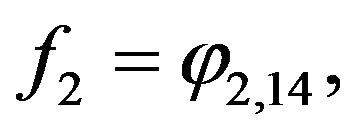 we have
we have
 (35)
(35)
Then none of the operators  and
and  does not dominates the other.
does not dominates the other.
4. Domination of Output Operators
In this section, we introduce and we study the notion of domination for observed systems (output operators) with respect to an input one. We consider first a dual problem where the control concerns the initial state, and then a general controlled system.
4.1. A Dual Problem
In this section, we examine a dual problem concerning the output operators and observed systems. We consider the system
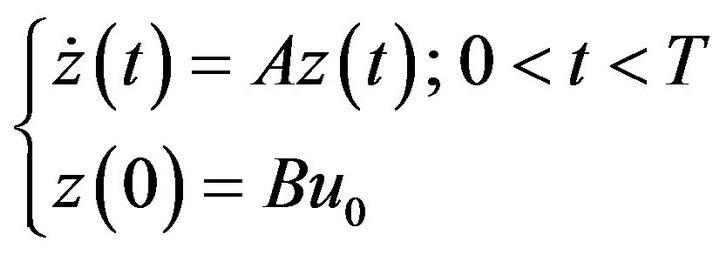 (36)
(36)
The initial state  depends on an input operator
depends on an input operator  and is of the form
and is of the form 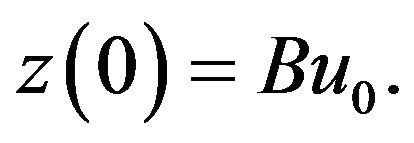 We assume that
We assume that  is a linear operator with a domain
is a linear operator with a domain 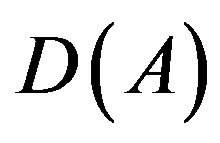 dense in
dense in , a separable Hilbert space, and generates a strongly continuous semi-group
, a separable Hilbert space, and generates a strongly continuous semi-group  on the state
on the state .
.
 ,
, 
 is a Hilbert space. The system
is a Hilbert space. The system  is augmented with the following output equations
is augmented with the following output equations
 (37)
(37)
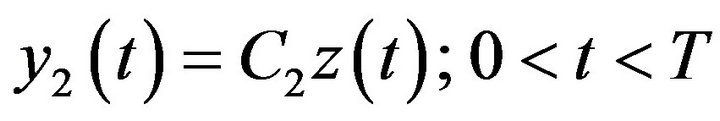 (38)
(38)
For ; the observations are given by
; the observations are given by

We have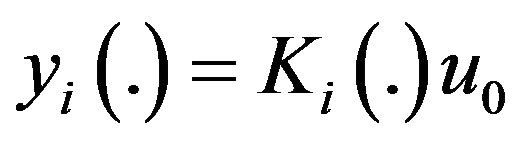 , with
, with

Its adjoint operator is defined by

Noting 
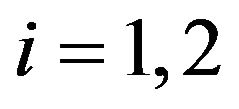 ;
; 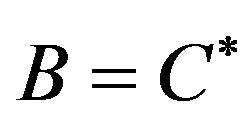 and considering the dual systems
and considering the dual systems
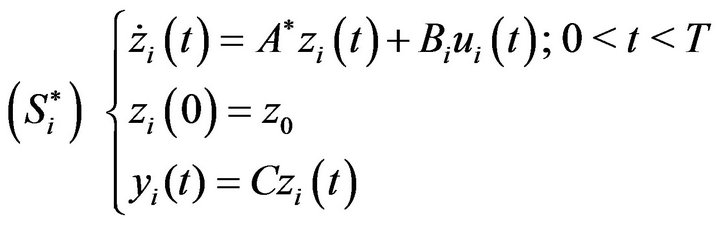
and

we obtain the following characterization result.
Proposition 11.  (respectively
(respectively
 ) if and only if, the controlled system
) if and only if, the controlled system
 dominates
dominates 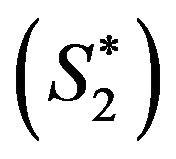 exactly (respectively weakly).
exactly (respectively weakly).
From this general result, one can deduce analogous results and similar properties to those given in previous sections.
4.2. Domination of Output Operators
We consider the following linear distributed system
 (39)
(39)
where  generates a s.c.s.g.
generates a s.c.s.g.  on the state space
on the state space ;
;  and
and 
 is the control space and the system (S) is augmented with the output equations
is the control space and the system (S) is augmented with the output equations

where 

 is an Hilbert space. The observation with respect to operator
is an Hilbert space. The observation with respect to operator 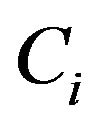 at the final time
at the final time  is given by
is given by
 (40)
(40)
We introduce hereafter the appropriate notion of domination for the considered case.
Definition 12. We say that 1)  dominates
dominates  exactly with respect to the system (S) (or the pair
exactly with respect to the system (S) (or the pair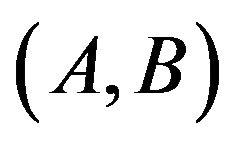 ) on
) on  if
if 
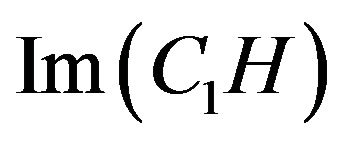 .
.
2) 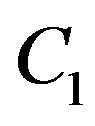 dominates
dominates  weakly with respect to the system (S) (or the pair
weakly with respect to the system (S) (or the pair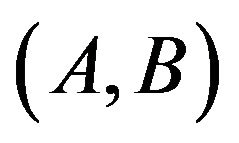 ) on
) on  if
if 
 .
.
Here also, we can deduce similar characterization results in the weak and exact cases. On the other hand, one can consider a natural question on a possible transitivity of such a domination. As it will be seen, this may be possible under convenient hypothesis. In order to examine this question, we consider without loss of generality, the linear distributed systems with the same dynamics 
 .
.
 (41)
(41)
 (42)
(42)
where  generates a s.c.s.g.
generates a s.c.s.g.  on the state space
on the state space ;
; ,
,  ,
, 
 ,
, ;
; 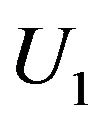 and
and  are two control spaces. The systems
are two control spaces. The systems  and
and 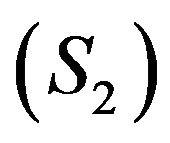 are augmented with the output equations
are augmented with the output equations


where , for
, for ;
; 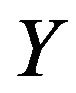 is a Hilbert space. The observations with respect to operator
is a Hilbert space. The observations with respect to operator  at the final time
at the final time  are respectively given by
are respectively given by
 (43)
(43)
 (44)
(44)
By the same, the observations with respect to operator 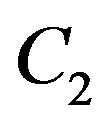 at time
at time 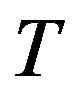 are given by
are given by
 (45)
(45)
 (46)
(46)
We have the following result deriving from the definitions.
Proposition 13. If the following conditions are satisfied 1)  dominates
dominates 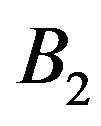 exactly (respectively weakly) with respect to operator
exactly (respectively weakly) with respect to operator 2)
2)  dominates
dominates  exactly (respectively weakly) with respect to operator
exactly (respectively weakly) with respect to operator 3)
3)  dominates
dominates  exactly (respectively weakly) with respect to operator
exactly (respectively weakly) with respect to operator then
then 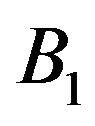 dominates
dominates  exactly (respectively weakly) with respect to operator
exactly (respectively weakly) with respect to operator .
.
We examine hereafter, the relationship between the notions of domination and compensation.
4.3. Domination and Compensation
In this section, we study the relationship between the notions of domination and compensation [7,8]. We consider without loss of generality, the following systems.
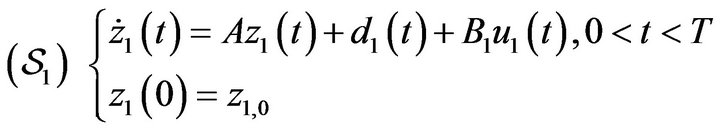 (47)
(47)
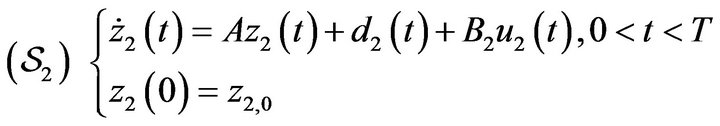 (48)
(48)
where 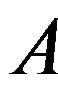 generates a s.c.s.g.
generates a s.c.s.g.  on the state space
on the state space ;
;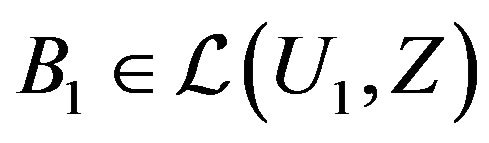 ,
, 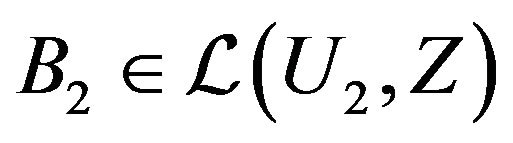 ,
, 
 ,
,  and
and ;
; 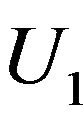 and
and 
are two control spaces. 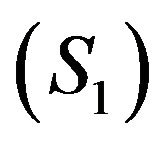 and
and 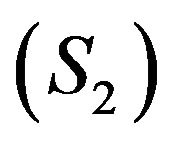 are respectively augmented with the output equations
are respectively augmented with the output equations
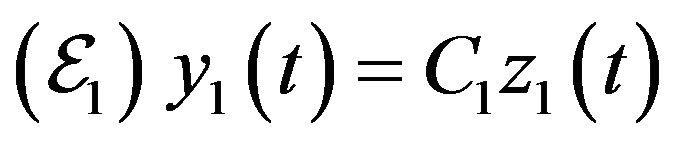
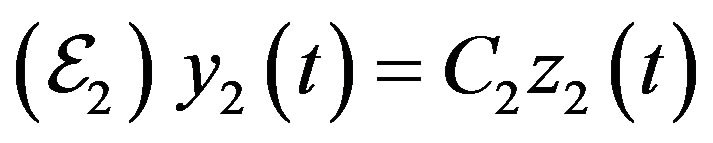
The states of these systems at the final time  are respectively given by
are respectively given by
 (49)
(49)

where the operators ;
; 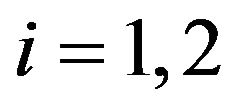 and
and  are defined by
are defined by
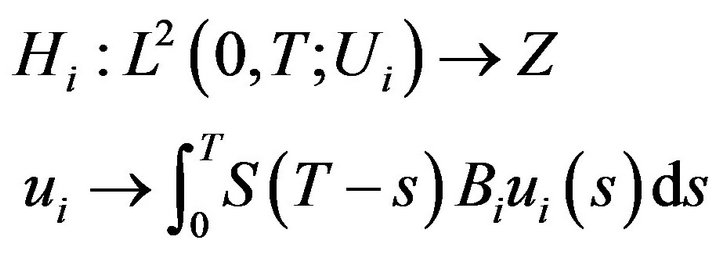 (50)
(50)
 (51)
(51)
The corresponding observations are given by
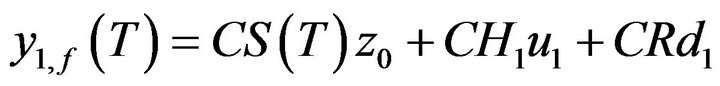 (52)
(52)
 (53)
(53)
and . First let us recall the notion of compensation.
. First let us recall the notion of compensation.
Definition 14. The system  augmented with output equation
augmented with output equation  (or
(or ) is 1) exactly remediable on
) is 1) exactly remediable on 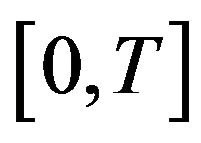 if for any
if for any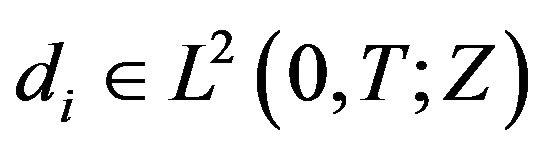 , there exists
, there exists 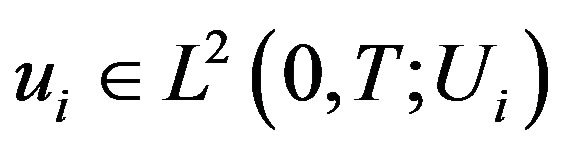 such that
such that , or equivalently
, or equivalently
 (54)
(54)
2) weakly remediable on 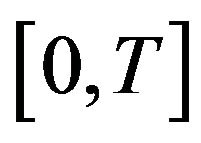 if for any
if for any 
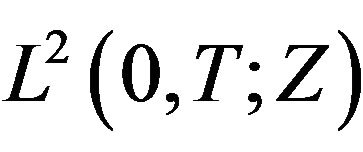 and any
and any  there exists
there exists 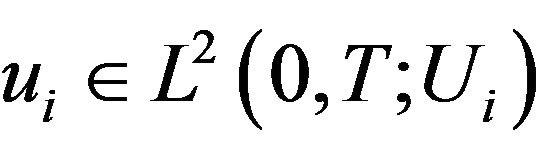
such that , or equivalently
, or equivalently
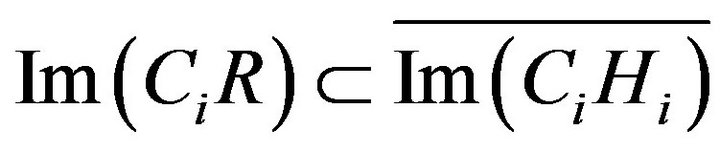 (55)
(55)
Here, the question is not to examine if a system is (or not) remediable (for this one can see [7,8]), but to study the nature of the relation between the notions of domination and compensation, respectively in the exact and weak cases. We have the following result.
Proposition 15. If the following conditions are verified 1)  is exactly (respectively weakly) remediable.
is exactly (respectively weakly) remediable.
2) 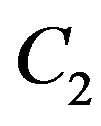 dominates
dominates  exactly (respectively weakly) with respect to the operator
exactly (respectively weakly) with respect to the operator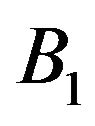 .
.
3)  (respectively
(respectively 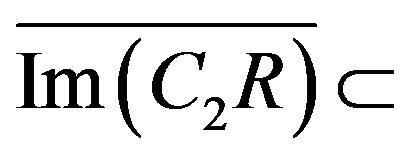
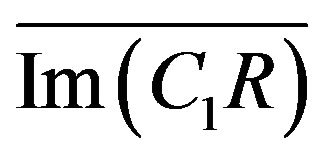 ).
).
then  is exactly (respectively weakly) remediable.
is exactly (respectively weakly) remediable.
We have the similar result concerning the output domination and the remediability notion.
Proposition 16. If the following conditions are satisfied 1)  is exactly (respectively weakly) remediable.
is exactly (respectively weakly) remediable.
2)  dominates
dominates  exactly (respectively weakly) with respect to the operator
exactly (respectively weakly) with respect to the operator .
.
then  is exactly (respectively weakly) remediable.
is exactly (respectively weakly) remediable.
Let us note that this section is a generalization of the previous one where  has the form
has the form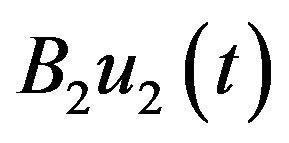 . The results can be applied easily to a diffusion system and to other systems and situations.
. The results can be applied easily to a diffusion system and to other systems and situations.
NOTES