Optimality Conditions and Second-Order Duality for Nondifferentiable Multiobjective Continuous Programming Problems ()
1. Introduction
Second-order duality in mathematical programming has been extensively investigated in the literature. In [1], Chen formulated second order dual for a constrained variational problem and established various duality results under an involved invexity-like assumptions. Subsequently, Husain et al. [2], have presented Mond-Weir type second order duality for the problem of [1], by introducing continuous-time version of second-order invexity and generalized second-order invexity. Husain and Masoodi [3] formulated a Wolfe type dual for a nondifferentiable variational problem and proved usual duality theorems under second-order pseudoinvexity condition while Husain and Srivastav [4] presented a MondWeir type dual to the problem of [2] to study duality under second-order pseudo-invexity and second-order quasiinvexity.
The purpose of this research is to present multiobjective version of the nondifferentiable variational problems considered in [2,4] and study various duality in terms of efficient solutions. The relationship between these multiobjective variational problems and their static counterparts is established through problems with natural boundary values.
2. Definitions and Related Pre-Requisites
Let  be a real interval,
be a real interval,  and
and  be twice continuously differentiable functions. In order to consider
be twice continuously differentiable functions. In order to consider  where
where  is differentiable with derivative
is differentiable with derivative , denoted by
, denoted by  and
and  the first order derivatives of
the first order derivatives of  with respect to
with respect to and
and , respectively, that is,
, respectively, that is,

Further denote by , and
, and  the
the  Hessian and
Hessian and  Jacobian matrices respectively.
Jacobian matrices respectively.
The symbols  and
and  have analogous representations.
have analogous representations.
Designate by X the space of piecewise smooth functions  with the norm
with the norm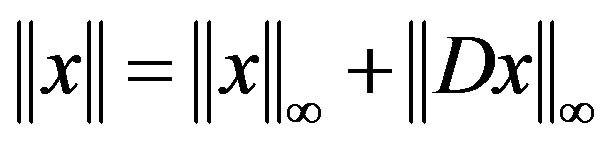 , where the differentiation operator D is given by
, where the differentiation operator D is given by

Thus  except at discontinuities.
except at discontinuities.
We incorporate the following definitions which are required for the derivation of the duality results.
Definition 1. (Second-order Invex): If there exists a vector function  where
where  and with
and with  at
at  and
and  such that for a scalar function
such that for a scalar function , the functional
, the functional  where
where  satisfies
satisfies

then  is second-order invex with respect to
is second-order invex with respect to
 where
where  and
and  the space of n-dimensional continuous vector functions.
the space of n-dimensional continuous vector functions.
Definition 2. (Second-order Pseudoinvex): If the functional  satisfies
satisfies

then  is said to be second-order pseudoinvex with respect to
is said to be second-order pseudoinvex with respect to .
.
Definition 3. (Second-order strict-pseudoinvex): If the functional  satisfies
satisfies

then  is said to be second-order pseudoinvex with respect to
is said to be second-order pseudoinvex with respect to .
.
Definition 4. (Second-order Quasi-invex): If the functional 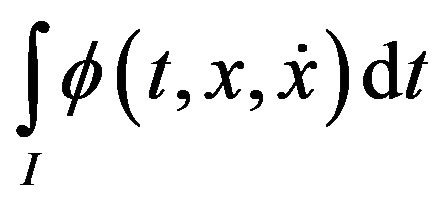 satisfies
satisfies
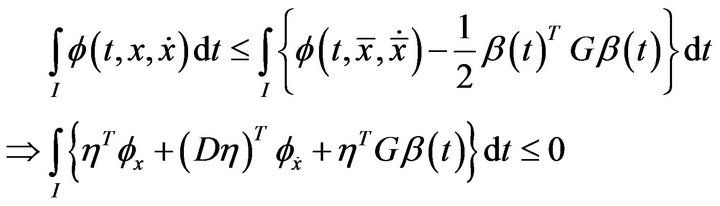
then  is said to be second-order quasi-invex with respect to
is said to be second-order quasi-invex with respect to .
.
Remark 1. If  does not depend explicitly on t, then the above definitions reduce to those for static cases.
does not depend explicitly on t, then the above definitions reduce to those for static cases.
The following inequality will also be required in the forthcoming analysis of the research:
Lemma: 1 (Schwartz inequality): It states that

with equality in (1) if  for some
for some 
Throughout the analysis of this research, the following conventions for the inequalities will be used:
If  with
with  and
and
 , then
, then

3. Statement of the Problem and Necessary Optimality Conditions
Consider the following nondifferentiable Multiobjective variational problem:
(VCP): Minimize

subject to
 (1)
(1)
 (2)
(2)

where 1)  denote the space of piecewise smooth functions x with norm
denote the space of piecewise smooth functions x with norm , where differentiation operator D already defined.
, where differentiation operator D already defined.

are assumed to be continuously differentiable functions, and 3) for each  is an
is an  positive semi definite (symmetric) matrix, with
positive semi definite (symmetric) matrix, with  continuous on I.
continuous on I.
In this section we will derive Fritz John and Karush-Kuhn-Tucker type necessary optimality conditions for (VCP).
Definition: A point  is said to be efficient solution of (VCP) if there exist
is said to be efficient solution of (VCP) if there exist  such that
such that

for some  and
and

for 
The following result which is a recast of a result of Chankong and Haimes [5] giving a linkage between an efficient solution of (VCP) and an optimal solution of p-single objective variational problem:
Proposition 1. (Chankong and Haimes [5]): A point  is an efficient solution of (VCP) if and only if
is an efficient solution of (VCP) if and only if  is an optimal solution of
is an optimal solution of  for each
for each 
 : Minimize
: Minimize

subject to


for obtaining the optimal conditions for (VCP) we will use the optimal conditions obtained by Chandra et al. [6] for a single-objective variational problem which does not contain integral inequality constraints of .
.
The validity of the following proposition is quite essential in obtaining the optimality conditions for (VCP)Proposition 2. If  is an efficient solution of (VCP), then
is an efficient solution of (VCP), then  is an optimal solution of the following problem
is an optimal solution of the following problem  for each
for each 
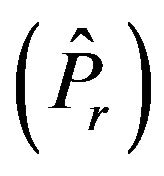 : Minimize
: Minimize

subject to


Proof: Let  be an efficient solution of (VCP). Suppose that
be an efficient solution of (VCP). Suppose that  is not optimal solution of
is not optimal solution of , for some
, for some  Then there exists an
Then there exists an  such that
such that

 (3)
(3)
and

The inequality (3) for 
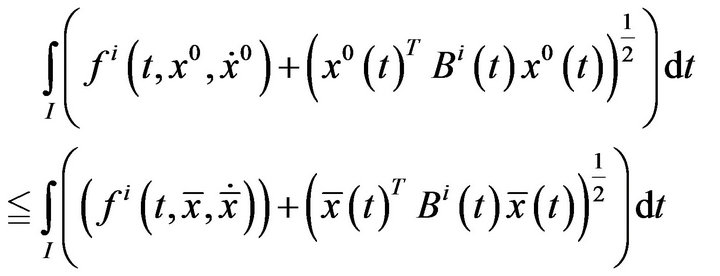 (4)
(4)
The inequalities (3) along with (4) contradicts the fact that  is an efficient solution of (VCP).
is an efficient solution of (VCP).
Hence  is an optimal solution of
is an optimal solution of , for some
, for some 
Theorem 1. (Fritz John Type necessary optimality condition): Let  be an efficient solution of (VCP). Then there exist
be an efficient solution of (VCP). Then there exist 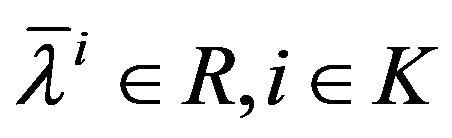 and piecewise smooth functions
and piecewise smooth functions 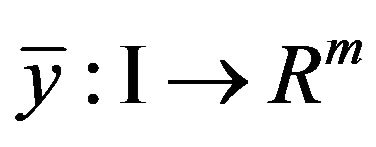 and
and  such that
such that
 (5)
(5)
 (6)
(6)
 (7)
(7)
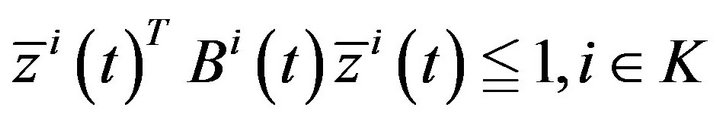 (8)
(8)
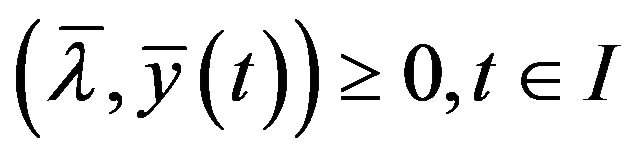 (9)
(9)
Proof: Since 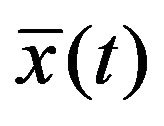 is an efficient solution of (VCP), by Proposition 2,
is an efficient solution of (VCP), by Proposition 2,  is an efficient solution of
is an efficient solution of 
for each  and hence in particular
and hence in particular . So by the results of [6] there exist
. So by the results of [6] there exist  and piecewise smooth functions
and piecewise smooth functions 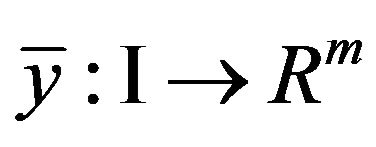 and
and  such that
such that

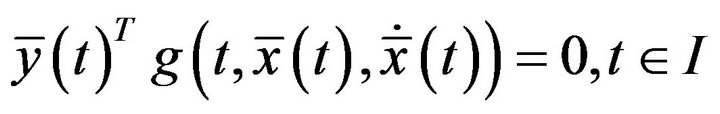
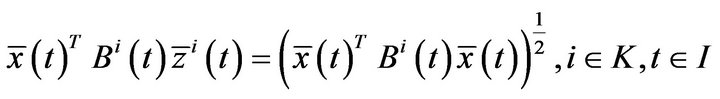
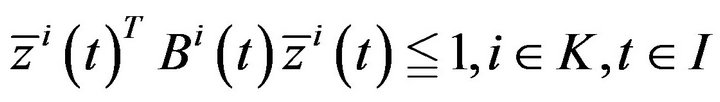

The above conditions yield the relations (5) to (9).
Theorem 2 (Kuhn-Tucker type necessary optimality condition):
Let 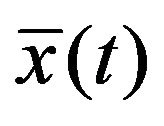 be an efficient solution of (VCP) and let for each
be an efficient solution of (VCP) and let for each , the conditions of
, the conditions of  satisfy Slaters or Robinson condition [6] at
satisfy Slaters or Robinson condition [6] at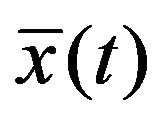 . Then there exist
. Then there exist  and piecewise smooth functions
and piecewise smooth functions  and
and 
 such that
such that
 (10)
(10)
 (11)
(11)
 (12)
(12)
 (13)
(13)
 (14)
(14)
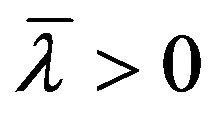 (15)
(15)
Proof: Since  is an efficient solution of (VCP) by Proposition 2,
is an efficient solution of (VCP) by Proposition 2,  is an optimal solution of
is an optimal solution of  for each
for each . Since for each
. Since for each , the contradicts of
, the contradicts of , satisfy Slaters or Robinson conditions [6] at
, satisfy Slaters or Robinson conditions [6] at , by Kuhn-Tucker necessary condition of [6], for each
, by Kuhn-Tucker necessary condition of [6], for each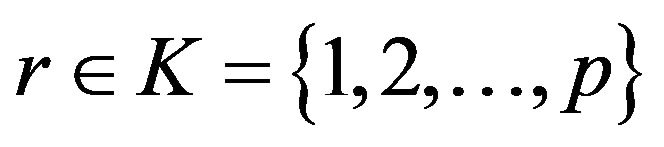 , there exist
, there exist  and piecewise smooth function
and piecewise smooth function  such that
such that





Summing over  we obtain
we obtain

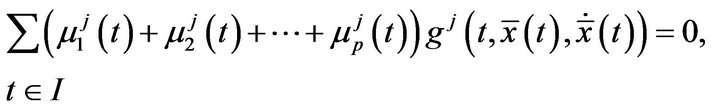
where  for each
for each 
These can be written as,


where 
and 
Setting

we get


That is

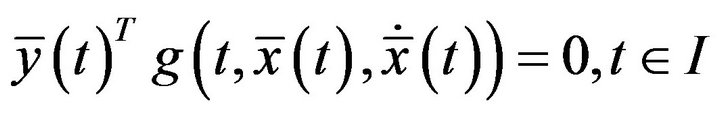




4. Mond-Weir Type Second Order Duality
In this section, we present the following Mond-Weir type second-order dual to (VCP) and validate duality results:
(M-WD): Maximize

subject to
 (16)
(16)
 (17)
(17)
 (18)
(18)
 (19)
(19)
where

and

We denote by CP and CD the sets of feasible solutions to (VCP) and (M-WD) respectively.
Theorem 3. (Weak Duality): Assume that
(A1)  and
and
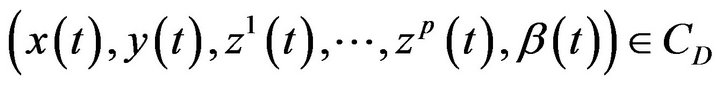 .
.
(A2)  is second-order pseudoinvex.
is second-order pseudoinvex.
(A3) 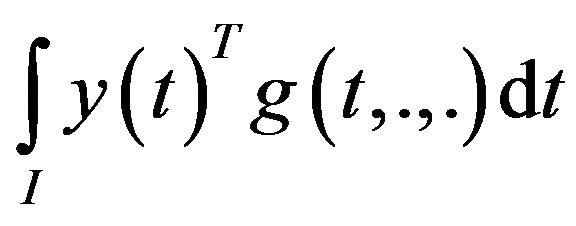 is second-order quasi-invex.
is second-order quasi-invex.
Then
 (20)
(20)
and
 (21)
(21)
cannot hold.
Proof. Suppose to the contrary, that (20) and (21) hold.
Since  we have
we have

Since 
we have
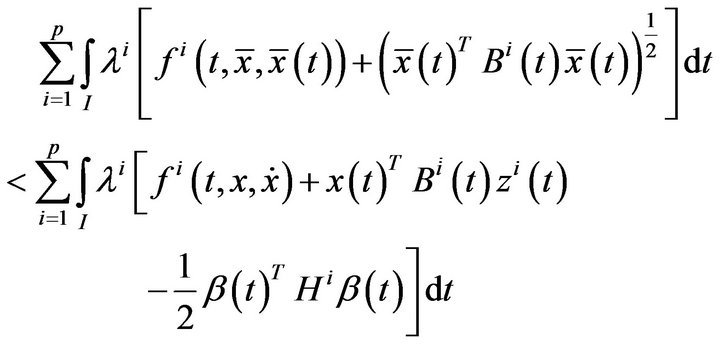
Now, by the constraints (2), (18) and (19), we have

This by (A3), yields

By integration by parts, we have


This, by using (4) gives
 (22)
(22)



By hypothesis (A1), it implies
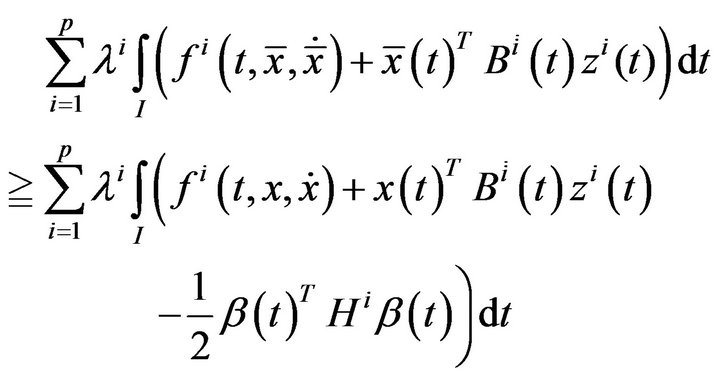
Using  in the above, we have
in the above, we have

This contradicts (20) and (21). Hence the result.
Theorem 4 (Strong duality): Let  be normal and is an efficient solution of (VP). Then there exist
be normal and is an efficient solution of (VP). Then there exist , a piecewise smooth function
, a piecewise smooth function 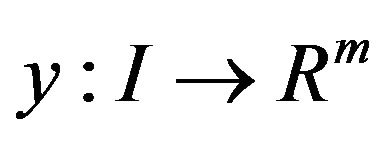 such that
such that  is feasible for (M-WD) and the two objective functions are equal. Furthermore, if the hypotheses of Theorem 3 hold for all feasible solutions of (VCP) and (M-WD) ,then
is feasible for (M-WD) and the two objective functions are equal. Furthermore, if the hypotheses of Theorem 3 hold for all feasible solutions of (VCP) and (M-WD) ,then  is an efficient solution of (M-WD).
is an efficient solution of (M-WD).
Proof: Since  is normal and an efficient solution of (VP), by Proposition 2, there exist
is normal and an efficient solution of (VP), by Proposition 2, there exist  and piecewise smooth
and piecewise smooth 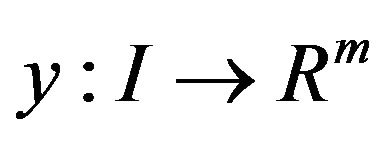 and
and 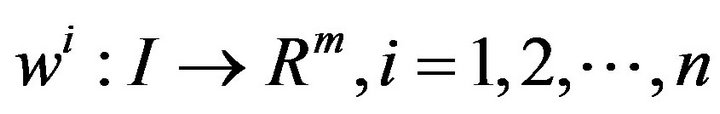 satisfying
satisfying
 (23)
(23)
 (24)
(24)
 (25)
(25)
 (26)
(26)
 (27)
(27)
From (24) along with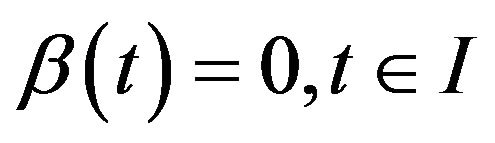 , we have
, we have

Hence

satisfies the constraints of (M-WD) and
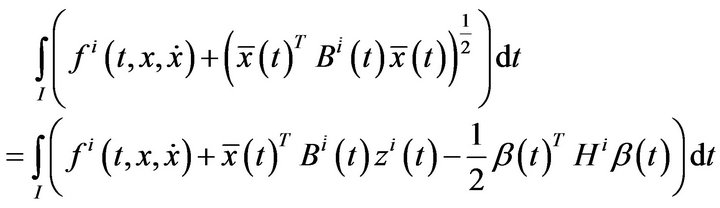
That is, the two objective functionals have the same value.
Suppose that  is not the efficient solution of (M-WD). Then there exists
is not the efficient solution of (M-WD). Then there exists 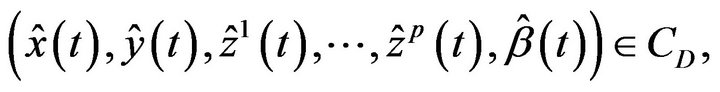 such that
such that

As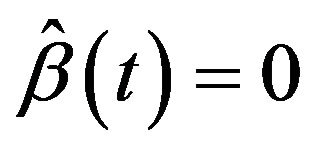 , we have
, we have

This contradicts the conclusion of Theorem 3. Hence  is an efficient solution of (M-WD).
is an efficient solution of (M-WD).
Theorem 5 (Converse duality):
(A1): Assume that  is an efficient solution of (M-WD)
is an efficient solution of (M-WD)
(A2): The vectors  are linearly independent where
are linearly independent where  the
the  row of is
row of is  and
and  is the
is the  row of G,
row of G,
(A3)
are linearly independent and
(A4) for  either a)
either a) 
and 
or b) 
and 
Then  is feasible for (VCP) and the two objective functionals have the same value. Also, if Theorem 3 holds for all feasible solutions of (CP) and (M-WD), the
is feasible for (VCP) and the two objective functionals have the same value. Also, if Theorem 3 holds for all feasible solutions of (CP) and (M-WD), the  is an efficient solution of (VCP).
is an efficient solution of (VCP).
Proof: Since  is an efficient solution of (M-WD), there exist
is an efficient solution of (M-WD), there exist ,
,  and
and , and piecewise smooth
, and piecewise smooth ,
,  ,
,  and
and  such that the following Fritz John optimality conditions (Theorem 1)
such that the following Fritz John optimality conditions (Theorem 1)
 (28)
(28)
 (29)
(29)
 (30)
(30)
 (31)
(31)
 (32)
(32)
 (33)
(33)
 (34)
(34)
 (35)
(35)
 (36)
(36)
 (37)
(37)
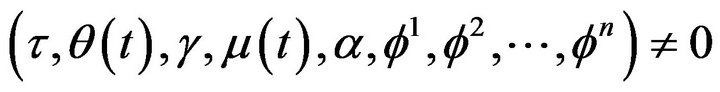 (38)
(38)
From (31), we have
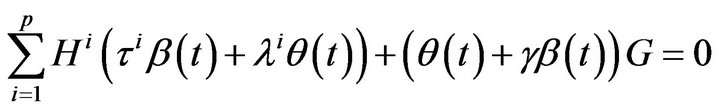 (39)
(39)
This, by the hypothesis (A2) gives
 (40)
(40)
and  (41)
(41)
Using (40), (41) and (17), we have
 (42)
(42)
Let  Then (41) gives
Then (41) gives  and (40) gives
and (40) gives ,
, 
Using  and
and , (42) implies
, (42) implies

This, because of (A3) yields
 (43)
(43)
The relation (43) with  gives
gives 
Since , (36) gives
, (36) gives 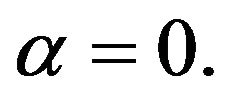 The relation (30) yields
The relation (30) yields  we have
we have ,
,  from (32) and
from (32) and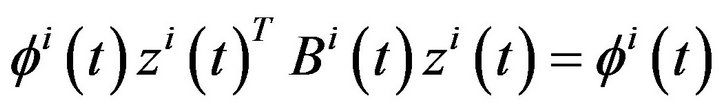 ,
,  ,
,  from (35). These yield
from (35). These yield ,
,  ,
, .
.
Consequently

contradicting (38).
Hence  and from (43)
and from (43) 
Multiplying (30) by , summing over j, and then using (34) and (41), we have
, summing over j, and then using (34) and (41), we have

In view of the hypothesis (A4), this gives ,
,
 , The relation (30) implies
, The relation (30) implies ,
,
 yielding the feasibility of
yielding the feasibility of  for (VCP).
for (VCP).
The relation (32) with  and
and  gives
gives
 (44)
(44)
This by Schwartz inequality gives
 (45)
(45)
If  then (35) give
then (35) give
 ,
, . and so (45 ) implies
. and so (45 ) implies
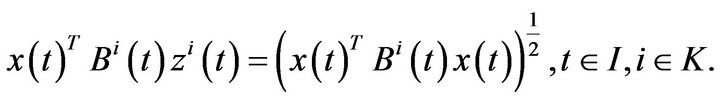
If  (44) gives
(44) gives . So we still get
. So we still get

Now suppose that  is not an efficient of (VCP). Then, there exists
is not an efficient of (VCP). Then, there exists  such that
such that

and

Using  and
and

We have

for some  and
and

This contradicts Theorem 3. Hence  is an efficient solution for (VCP).
is an efficient solution for (VCP).
Theorem 6 (Strict converse duality): Assume that
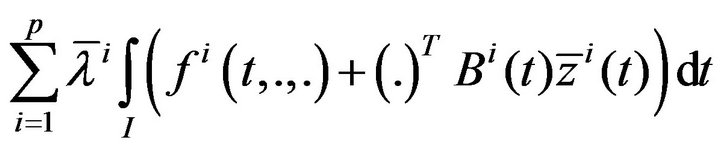
is second-order strictly pseudoinvex, and
 is second-order quasi-invex with respect to same
is second-order quasi-invex with respect to same . Assume also that (VCP) has an optimal solution
. Assume also that (VCP) has an optimal solution  which is normal [6]. If
which is normal [6]. If  is an optimal solution of (M-WD), then
is an optimal solution of (M-WD), then  is an efficient solution of (VCP) with
is an efficient solution of (VCP) with 
Proof: We assume that  and exhibit a contradiction. Since
and exhibit a contradiction. Since  is an efficient solution, it follows from Theorem, that there exist
is an efficient solution, it follows from Theorem, that there exist ,
,  ,
, 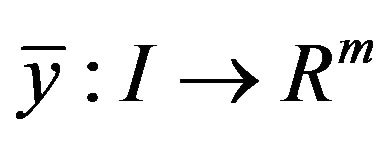 ,
,  ,
,  ,
,  and
and  such that
such that
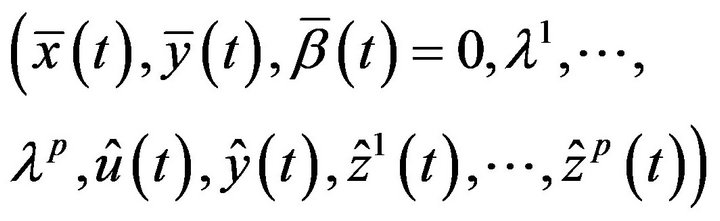
is an efficient solution of (M-WD). Since 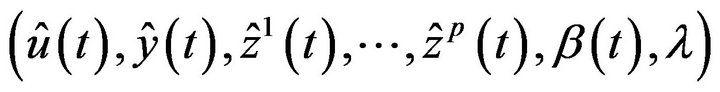 is an optimal solution of (M-WD), it follows that
is an optimal solution of (M-WD), it follows that

This, because of second-order strict-pseudoinvexity of
 (46)
(46)
Also from the constraint of (VCP) and (M-WD), we have
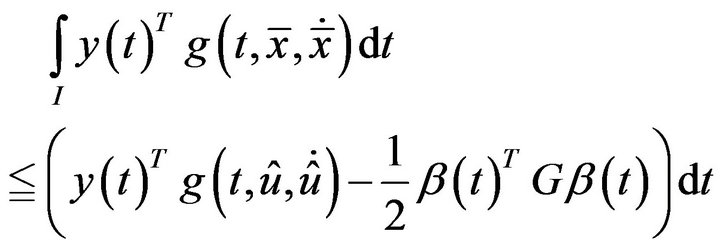
Because of second-order quasi-invexity of
 , this implies
, this implies
 (47)
(47)
Combining (46) and (47), we have

(By integrating by parts)
This, by using η = 0, at t = a and t = b, implies

contradicting the feasibility of
 for (M-WD).
for (M-WD).
5. Problems with Natural Boundary Values
In this section, we formulate a pair of nondifferentiable Mond-Weir type dual variational problems with natural boundary values rather than fixed end points given bellow
 : Minimize
: Minimize

Subject to

 : Maximize
: Maximize

Subject to




 and
and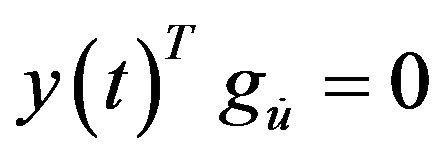 , at
, at .
.

We shall not repeat the proofs of Theorems 3-6 for the above problems, as these follow on the lines of the analysis of the preceding section with slight modifications.
6. Non-Linear Multiobjective Programming Problem
If the time dependency of  and
and  is ignored, then these problems reduce to the following nondifferentiable second-order nonlinear problems already studied in the literature:
is ignored, then these problems reduce to the following nondifferentiable second-order nonlinear problems already studied in the literature:
(VP1): Minimize

subject to

(VD1): Maximize

subject to

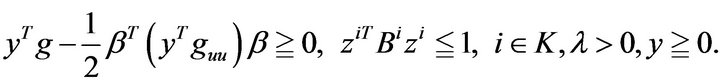
NOTES