Electromagnetic nature of the nuclear forces and toroid structure of the deuteron and triton ()
1. INTRODUCTION
In order for a complete theory of the atomic nucleus to be created, that theory has to be able to explain the structure of the nucleus and the available experimental data about its behavior [1-4]. The main difficulty here is the incomplete knowledge of the forces of interaction between nucleons inside the nuclei and their models.
In the field of elementary particles there are two leading models: standard and helicon.
The standard model [5-7] presents elementary particles as quantum objects that can be both wave and particle. As particles they have mass, charge, spin, magnetic moment, quadrupole moment. The elementary particles mainly are modelling with spheres.
The helicon model [8-11], or ring model is less wellknown. According to that model the particles have ring spiral structure of charged filaments, one or more. The filaments are superconductors coiled around an imaginary ring. The helicon model is consistent with all the widely accepted and experimentally verified properties of elementary particles. This model implies the assumption that all known types of interactions (strong, electroweak, gravitational) should be electromagnetic in nature.
In [12] we introduce a toroid model of the nucleons that is to a certain degree in contradiction with the standard model, but it is in full agreement with the helicon model.
We consider the nucleons as tori, rotating with a constant angular velocity around an axis z, passing through their mass (geometrical) centre O and perpendicular to the plane of rotation of their central circle. From quantum mechanical point of view the nucleon is not a localized object in the three-dimensional physical space and therefore it cannot be consider a sphere or a torus [13]. We feel such a model is appropriate in the formal-heuristic sense of Niels Bohr. It is similar to the old quantum theory model of the electron in the hydrogen atom for which Bohr obtains good results for the description of its spectrums. Modern quantum theory confirms Bohr’s results based on other concepts.
Formal approaches are widely used in physics. In classical mechanics for example a variety of formulations have been proposed by Lagrange, Hamilton and others. The best example in that sense is quantum mechanics, where one introduces the so-called wave function which allows for the theoretical derivation of a number of physical properties confirmed extremely well by experiment.
We consider nucleons within nuclei to be space dimensional objects—tori, within which the electrical charges can be redistributed. This assumption does not contradict the quark model. The latter enables us to determine the electrostatic interaction between them. Based on this model, we obtained that the strong interactions are electromagnetic in nature. To achieve this we used exact analytical formulas first obtained by us about the electrostatic interaction between two charged conducting spheres with arbitrary charges and radii [14].
In this paper we apply this method in order to obtain the electrostatic interaction between nucleons in the nuclei of deuterium and tritium.
As noted by Feynman [15], at distances under 10–15 m either Coulomb’s law is not in force or the electrons and protons are not point charges. We consider the proton-neutron couples at distances under 10–15 m. Thus in this paper we determine that the known binding energy between the nucleons in the deuteron and triton is obtained through electromagnetic interactions! We also explain the other basic experimental data—spin, magnetic moment, stability of the nuclei of deuterium and tritium. Doing that, we use the experimentally obtained values of the radii and masses of the nucleons and the nuclei.
We obtain the volumes and mass densities of the nucleons; we also obtain the force of interaction within the nuclei under consideration—results obtained for the first time in nuclear physics.
2. METHOD FOR FINDING OUT ELECTROSTATIC INTERACTION BETWEEN TWO CHARGED CONDUSTIVE SPHERES
We will represent the part of the method presented by us in [10], necessary for performing the calculations for the nuclei of deuterium and tritium.
Let S1 and S2 be two isolated charged conductive spheres, with charges Q1, Q2 and radii r1, r2 respectively. Let’s denote with R the distance between their centers O1, O2 in an inertial system J. Since charges Q1 and Q2 are evenly distributed on the surfaces of S1 and S2, it is assumed that before the interaction between the spheres they are concentrated in the centers O1 and O2 respectively.
As a result of the electrostatic interaction between S1 and S2, on their surfaces appear induced charges  and
and , which are interrelated. Formally, we can consider that these charges are located on line segment
, which are interrelated. Formally, we can consider that these charges are located on line segment . On the surfaces of S1 and S2 appear uniformly distributed charges
. On the surfaces of S1 and S2 appear uniformly distributed charges  and
and , we can assume that they are concentrated in their canters O1 and O2.
, we can assume that they are concentrated in their canters O1 and O2.
From the law for preservation of electric charges are in power the equations:
 and
and (1)
(1)
We will determine the charges ,
, 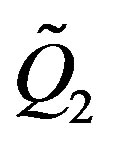 and hence the charges
and hence the charges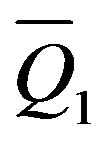 ,
, . Let as a consequence of
. Let as a consequence of  be generated image charges
be generated image charges 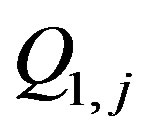 (j = 1, 2, 3, ∙∙∙). Because each charge
(j = 1, 2, 3, ∙∙∙). Because each charge  generates
generates , the charges with an odd index
, the charges with an odd index  (m = 1, 2, 3, ∙∙∙) are located in the sphere
(m = 1, 2, 3, ∙∙∙) are located in the sphere , and charges with an even index
, and charges with an even index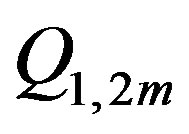 —in the sphere
—in the sphere . Similarly are determined the image charges
. Similarly are determined the image charges  (j = 1, 2, 3, ∙∙∙), arising as a consequence from charge
(j = 1, 2, 3, ∙∙∙), arising as a consequence from charge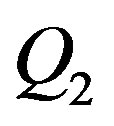 . The charges with an odd index
. The charges with an odd index  (m = 1, 2, 3 ∙∙∙) are located in the sphere
(m = 1, 2, 3 ∙∙∙) are located in the sphere , and charges with an even index
, and charges with an even index —in the sphere
—in the sphere .
.
Let’s denote 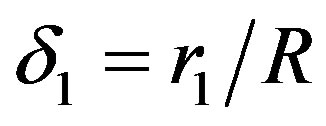 and
and . We introduce for j = 1, 2, 3, ∙∙∙ the following denotations:
. We introduce for j = 1, 2, 3, ∙∙∙ the following denotations:
 (2)
(2)
If 
 are the distances of imagecharges
are the distances of imagecharges , respectively to the centers of the spheres
, respectively to the centers of the spheres , in [14] we obtain that:
, in [14] we obtain that:
 (3)
(3)
We find also that:
 (4)
(4)
Lets
 (5)
(5)
where  at
at 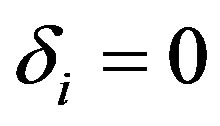 (
( ).
).
Since charges  and
and 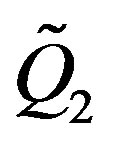 are sums of all image charges, located respectively in the spheres
are sums of all image charges, located respectively in the spheres  and
and , then
, then
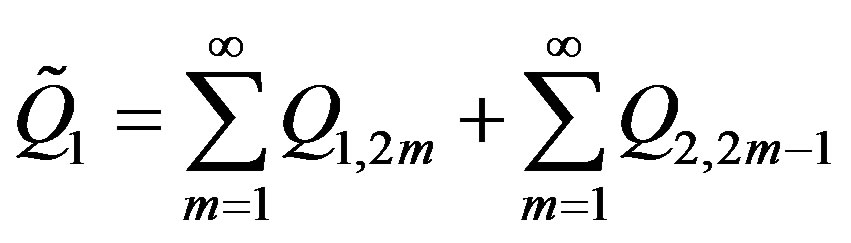
and
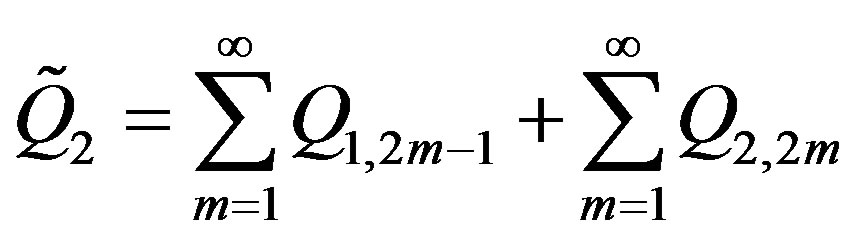
From here and from (4) and (5) it follows that
 and
and 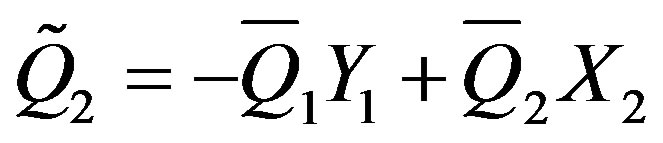
Then, substituting these equations in (1), we get:
 (6)
(6)
Lets denote the charges from formulas (4) and (6), which are located in the sphere  as
as , and those located in the sphere
, and those located in the sphere  as
as  (
( ). Thus
). Thus  and
and , and for
, and for ,
,  ,
,  and
and ,
,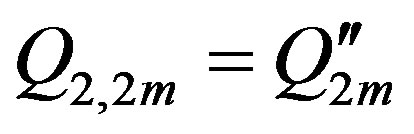 . Their corresponding distances to the centers of the spheres, where they are situated, we denote with
. Their corresponding distances to the centers of the spheres, where they are situated, we denote with  and
and 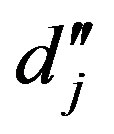 (
( ), where
), where .
.
If , and
, and , then, according to Coulomb’s law, for the magnitude F of the projection of the force of interaction on
, then, according to Coulomb’s law, for the magnitude F of the projection of the force of interaction on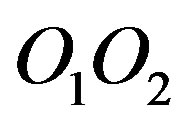 , acting on the spheres
, acting on the spheres  and
and  , we obtain
, we obtain
 (7)
(7)
The potential energy of interaction between the spheres 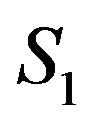 and
and , according to [16], is
, according to [16], is
 (8)
(8)
Let us point out that in (7) and (8) we do not take into consideration the interactions between the charges inside the spheres  and
and  as actually the interaction is external—between the charges on the surface of
as actually the interaction is external—between the charges on the surface of  with the charges on the surface of
with the charges on the surface of .
.
Let M be an arbitrary point in the electric field created by charges  and
and  (
( ). If M is at distances
). If M is at distances  and
and  from charges
from charges  and
and  respectively, then, using the metric relationships in a triangle, we can determine
respectively, then, using the metric relationships in a triangle, we can determine
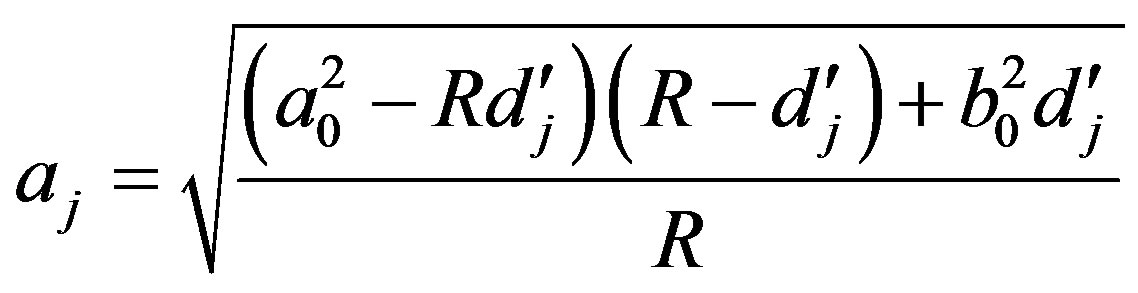
and
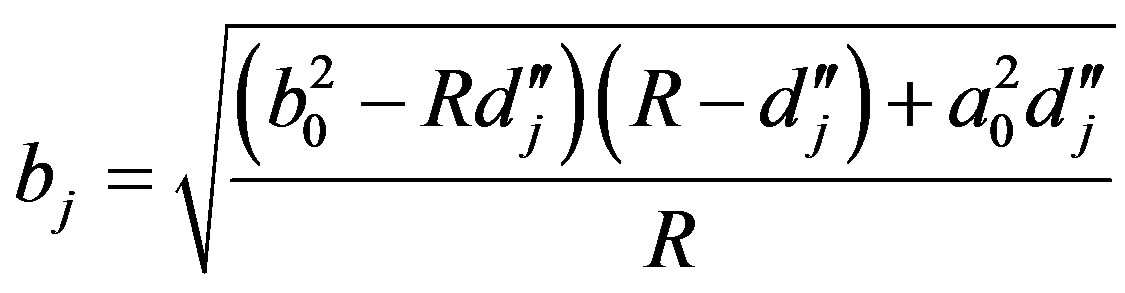
Then based on the principle of linear superposition of states, the potential at point M will be the sum of the potentials of all charges in M [16]. Therefore
 (9)
(9)
It is worthwhile to mention that using Eqs.7-9 one can determine the interaction between two charged spheres for arbitrary small distances between them, which represents a result obtained for the first time.
3. TOROID MODEL OF NUCLEONS
Using the results from [14] in [12] we first consider the nucleons as spheres, as they are viewed in the standard model. In this case we show that at distances 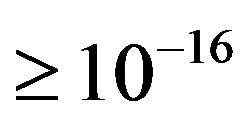 m we can calculate with good approximation the binding energy and force of interaction between nucleons by modeling protons as point charges. But at distances
m we can calculate with good approximation the binding energy and force of interaction between nucleons by modeling protons as point charges. But at distances 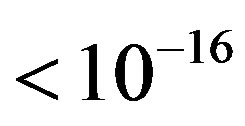 m the proton should not be considered as a point charge. We also found out that using the standard model the binding energy of triton cannot be obtained. Using this model it is difficult to explain the experimentally obtained magnetic moments of the nuclei relative to the magnetic moments of the comprising nucleons; it is also hard to explain the experimental results for the radii and stability of the nuclei.
m the proton should not be considered as a point charge. We also found out that using the standard model the binding energy of triton cannot be obtained. Using this model it is difficult to explain the experimentally obtained magnetic moments of the nuclei relative to the magnetic moments of the comprising nucleons; it is also hard to explain the experimental results for the radii and stability of the nuclei.
For this reason we remodel the nucleons as tori [12]. At that they are rotating with a constant angular velocity around a straight axis z, passing through their mass (geometrical) center O and perpendicular to the plane of rotation of their central circle (Figure 1).
After that we study a system of proton and neutron in order to determine the electrostatic interaction between them.
The two tori—of the proton and neutron we denote correspondingly as  and
and  and their centers as
and their centers as  and
and . We also assume that the central circles of
. We also assume that the central circles of  and
and  lie in parallel or coincident planes and rotate in the same or opposite directions with constant angular velocity around a the straight line z passing through
lie in parallel or coincident planes and rotate in the same or opposite directions with constant angular velocity around a the straight line z passing through  and
and , and perpendicular to the plane of their rotation. Thus if
, and perpendicular to the plane of their rotation. Thus if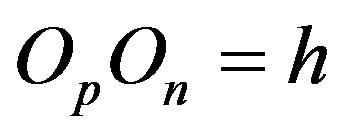 , then
, then 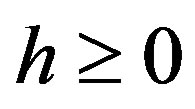 (Figure 2).
(Figure 2).
Let us denote by 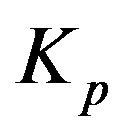 and
and  the centers of the forming circles of the tori
the centers of the forming circles of the tori  and
and , and with
, and with 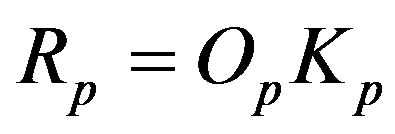 and
and —the radii of the central circles of
—the radii of the central circles of  and
and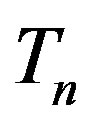 . We assume that
. We assume that  and
and  are at a distance
are at a distance  from each other.
from each other.
According to experimental data the radius of the proton  is smaller than the radius of the neutron
is smaller than the radius of the neutron . Because of that we consider
. Because of that we consider .
.
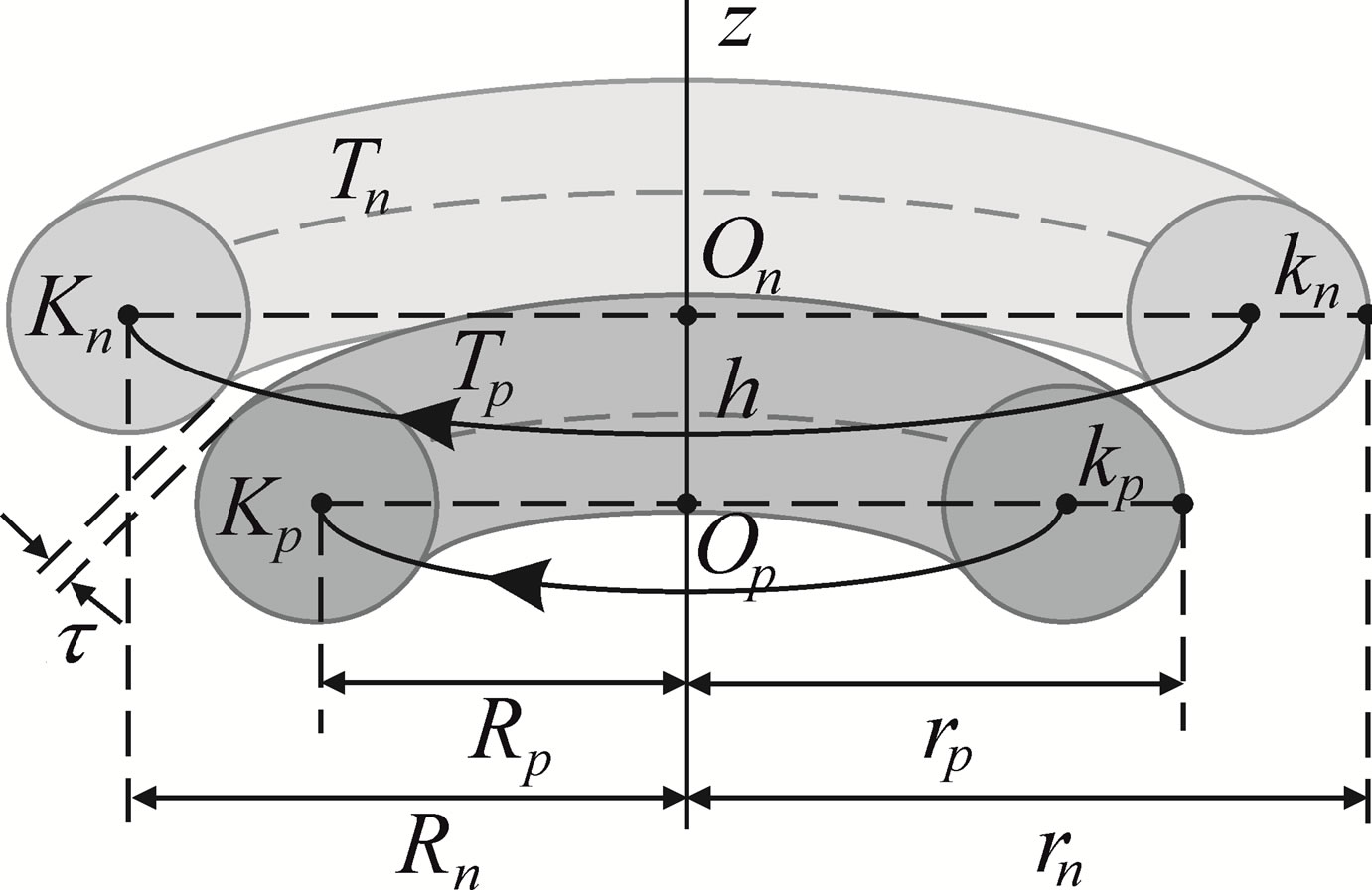
Figure 2. Cross section of a proton-neutron system.
Let  and
and  be the radii of the forming circles
be the radii of the forming circles 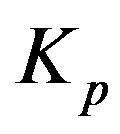 and
and . It is clear that
. It is clear that , and
, and . Besides that
. Besides that
 (10)
(10)
where  and
and  are the corresponding radii of the proton and neutron in this configuration. It should be noted that for different nuclei
are the corresponding radii of the proton and neutron in this configuration. It should be noted that for different nuclei ,
, 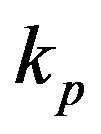 ,
, 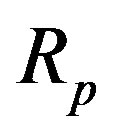 and
and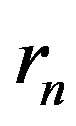 , v,
, v,  may have different values.
may have different values.
From geometrical considerations for  will be fulfilled the equation
will be fulfilled the equation
 (11)
(11)
It is clear that .
.
We assume that the volume mass densities of the proton and neutron are equal, i.e. . The volumes of the tori
. The volumes of the tori  and
and , according to [17], are correspondingly
, according to [17], are correspondingly 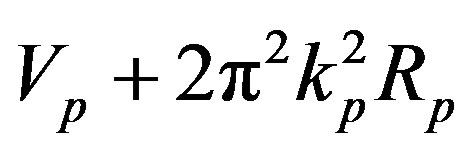 and
and . Then if
. Then if  and
and  are the corresponding masses of
are the corresponding masses of 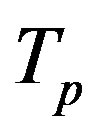 and
and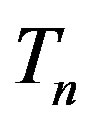 then from
then from  it follows that
it follows that
 (12)
(12)
In (12) we can substitute the experimentally measured masses of the proton and the neutron [18]  kg,
kg,  kg.
kg.
Lets denote with 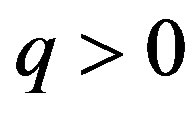 the radius of the empty part of the circle with a radius
the radius of the empty part of the circle with a radius . Then
. Then
 (13)
(13)
Further let  and
and 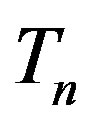 from Figure 2 be a protonneutron couple bound in the nucleus of deuterium or tritium. If we denote with
from Figure 2 be a protonneutron couple bound in the nucleus of deuterium or tritium. If we denote with  the radius of the nucleus under consideration, then
the radius of the nucleus under consideration, then .
.
In order to apply the results from Section 2 for spheres we will remodel the tori.
We will emphasize that the potential energy and the force of interaction between two spheres depend on the distance between image-charges, i.e. from the lengths of the line segments 
 from formula (3). These lengths in (3) are determined from the squares of the radii
from formula (3). These lengths in (3) are determined from the squares of the radii 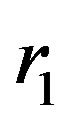 or
or  of the spheres and from the length of their central line
of the spheres and from the length of their central line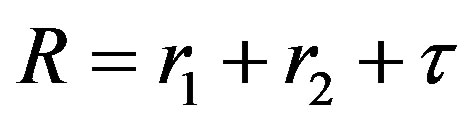 , where
, where  is the smallest distance between their surfaces. For the square of the radii of each of the two spheres is fulfilled
is the smallest distance between their surfaces. For the square of the radii of each of the two spheres is fulfilled ,
, 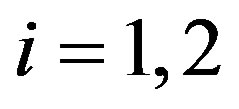 , where
, where  is the surface area of the corresponding sphere. Therefore, when we remodel the tori of the proton and the neutron we have to keep both their surface areas
is the surface area of the corresponding sphere. Therefore, when we remodel the tori of the proton and the neutron we have to keep both their surface areas 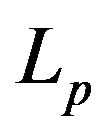 and
and  and the distance
and the distance  between them.
between them.
Due to the central symmetry of the charge of the proton we can consider all of its charge 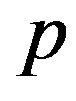 to be concentrated in the geometrical center
to be concentrated in the geometrical center  of the torus
of the torus .
.
Therefore we remodel the proton as a sphere , with radius
, with radius  and the same centre
and the same centre 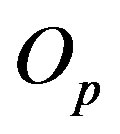 on the straight line z and a surface area equivalent to the torus surface area, i.e. it has the same surface area as the torus
on the straight line z and a surface area equivalent to the torus surface area, i.e. it has the same surface area as the torus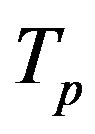 . At that
. At that  is charged with a charge
is charged with a charge 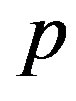 that is centrally symmetrical and can be redistributed.
that is centrally symmetrical and can be redistributed.
The surface area  of a torus
of a torus  according to [17] is
according to [17] is
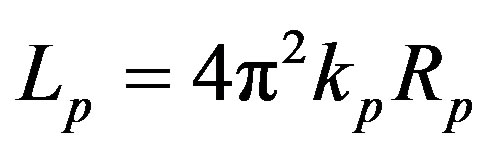 (14)
(14)
Then, as the surface areas of the torus 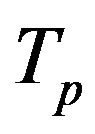 and the sphere
and the sphere  are equal, then from (14) it follows that the radius of
are equal, then from (14) it follows that the radius of  is
is
 (15)
(15)
We remodel the neutron  with a torus
with a torus  with an equivalent surface area. At that
with an equivalent surface area. At that  has the same center
has the same center  on z and its surface is at the same distance
on z and its surface is at the same distance  from the surface of
from the surface of  as in the case of
as in the case of  and
and  (Figure 3).
(Figure 3).
Let  be a sphere. Its central circle, is forming for the torus
be a sphere. Its central circle, is forming for the torus . We denote the centre of
. We denote the centre of  with
with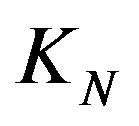 , at that
, at that  and with
and with —the radius of
—the radius of . Thus if
. Thus if  then
then  and from
and from 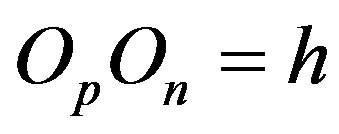 it follows that
it follows that , i.e.
, i.e.
 (16)
(16)
It is clear that  and
and .
.
From the equality of the surface areas  and
and  of the tori
of the tori  and
and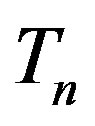 , it follows that
, it follows that
 (17)
(17)
For the number  of spheres
of spheres  which have total surface area equal to the surface area of the torus
which have total surface area equal to the surface area of the torus 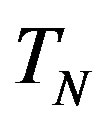 is fulfilled
is fulfilled . Therefore
. Therefore
 (18)
(18)
We assume that the centre  is motionless relative to the inertial reference system J. We introduce a solid non-inertial reference system G that rotates with the constant angular velocity
is motionless relative to the inertial reference system J. We introduce a solid non-inertial reference system G that rotates with the constant angular velocity  of rotation of
of rotation of  relative to J. At that, the point
relative to J. At that, the point  is the centre of the coordinate system
is the centre of the coordinate system , stationary connected with G and relative to which the spheres
, stationary connected with G and relative to which the spheres  and
and  are motionless to each other (Figure 3).
are motionless to each other (Figure 3).
Then for the experimentally obtained value of , giving values to q, from Eqs.10-13 we calculate
, giving values to q, from Eqs.10-13 we calculate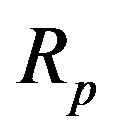 ,
,  ,
,  ,
,  and
and . With those and formula (15) we obtain the radius
. With those and formula (15) we obtain the radius  of the surface-equivalent sphere
of the surface-equivalent sphere . Varying
. Varying  m and
m and
 , from formulas (16) and (17) wecalculate the radius
, from formulas (16) and (17) wecalculate the radius  of the forming sphere
of the forming sphere .
.
Thus at , through formulas (7) and (8), we find the binding energy
, through formulas (7) and (8), we find the binding energy 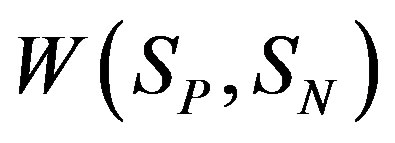 and force of interaction
and force of interaction . According to (18), the binding energy
. According to (18), the binding energy 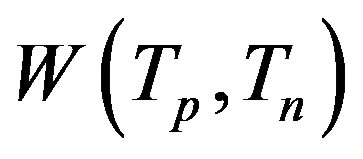 and force of interaction
and force of interaction  between a the proton and the neutron will be
between a the proton and the neutron will be
 (19)
(19)
The Eqs.19 are valid because the forming spheres of the torus  are situated symmetrically relative to the centre of the sphere
are situated symmetrically relative to the centre of the sphere .
.
Moving on we will structure the nuclei of deuterium and tritium. The positioning of the nucleons in them must correspond to the principle of minimum potential energy. Due to the mass defect in the nucleus, the potential energy of the interaction in the atomic nuclei is calculated by the following formula [2]:
 (20)
(20)
Here 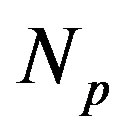 is the number of the protons,
is the number of the protons,  – number of the neutrons;
– number of the neutrons;  kg and
kg and  kg are the masses of the proton and of the neutron, respectively [18] and
kg are the masses of the proton and of the neutron, respectively [18] and  is the mass of the considered nucleus;
is the mass of the considered nucleus;  m·s–1 is the velocity of the light in flat vacuum [18]. We will find the values of
m·s–1 is the velocity of the light in flat vacuum [18]. We will find the values of  according to our method with formula (8), comparing them with the values obtained through formula (20).
according to our method with formula (8), comparing them with the values obtained through formula (20).
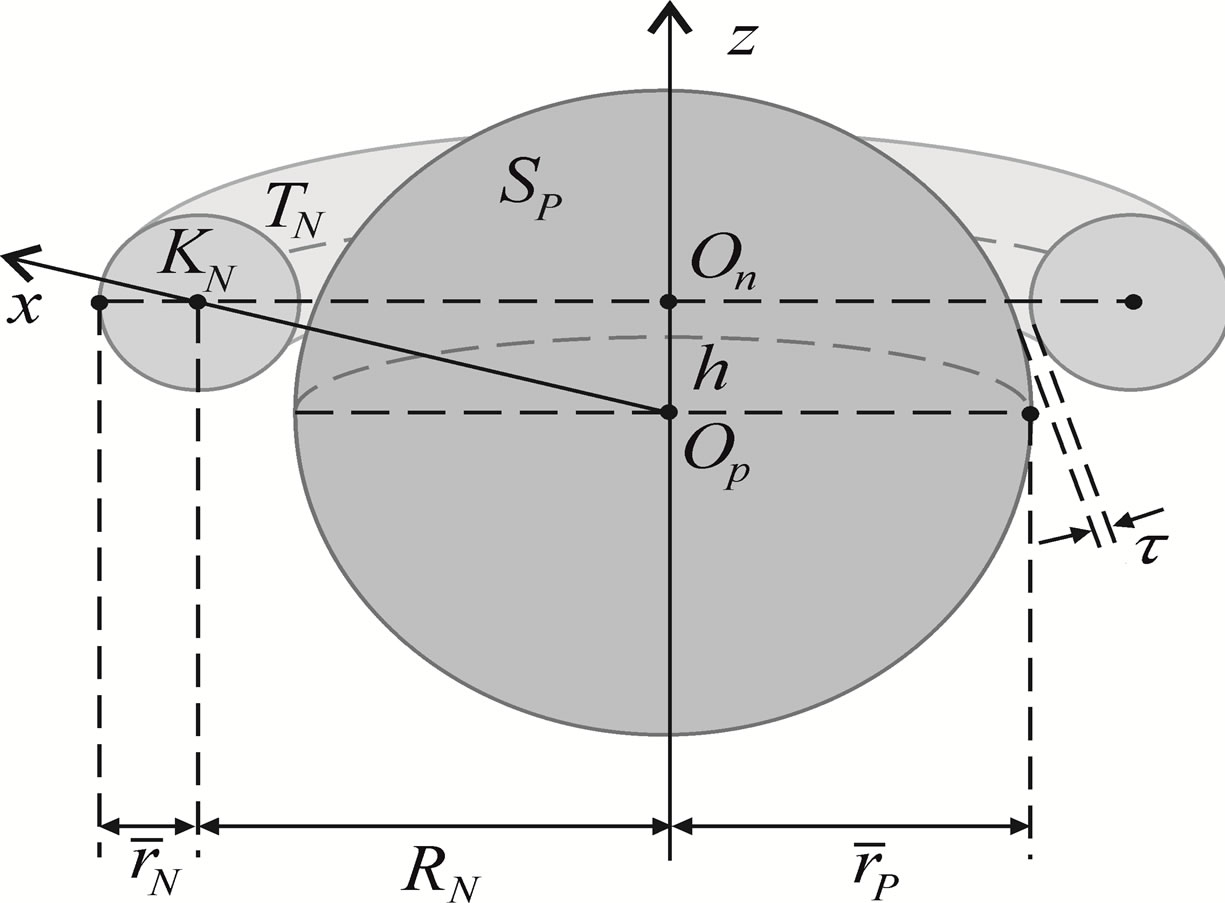
Figure 3. Cross section of reduced model of the proton-neutron system.
Let us consider the proton in a unbound state as a torus . Its radius according to [19] is
. Its radius according to [19] is  m. If
m. If  is the center of the forming circle of
is the center of the forming circle of , then we denote as
, then we denote as  the radius of this circle and with
the radius of this circle and with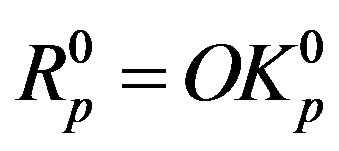 .
.
Using formulas (10) and (13) for different values of the radius of the circle of the empty part q we find ,
,  ,
,  and
and . We also find the volume
. We also find the volume  of the neutron in a free state since we know its mass
of the neutron in a free state since we know its mass  and we have assumed that
and we have assumed that . All the data are given in Table 1" target="_self"> Table 1.
. All the data are given in Table 1" target="_self"> Table 1.
In Table 1 we have denoted with  the radius of the forming circle of the torus of the proton and with
the radius of the forming circle of the torus of the proton and with  the radius of the central circle of the torus of the proton.
the radius of the central circle of the torus of the proton.
Due to the mass defect in atomic nuclei the volumes of the nucleons within them change. We will assume however that the volume mass densities of the proton and neutron do not change, i.e. .
.
4. MODEL OF THE DEUTERON
We model the nucleus of deuterium as two concentric toroids inlaid one in the other. The internal torus  corresponds to the proton and the external one
corresponds to the proton and the external one  corresponds to the neutron with
corresponds to the neutron with 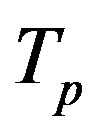 and
and  being at a distance
being at a distance  m. This configuration provides symmetry relative to the center of masses O of the deuteron placed in its geometrical center (Figure 4). From that follows the stability of the deuteron
m. This configuration provides symmetry relative to the center of masses O of the deuteron placed in its geometrical center (Figure 4). From that follows the stability of the deuteron .
.
We assume that both tori spin in the same direction with a constant angular velocity  around the line z going through their common center
around the line z going through their common center  and perpendicular to their plane of rotation.
and perpendicular to their plane of rotation.

Table 1. Size, volume and mass density of the proton and neutron.
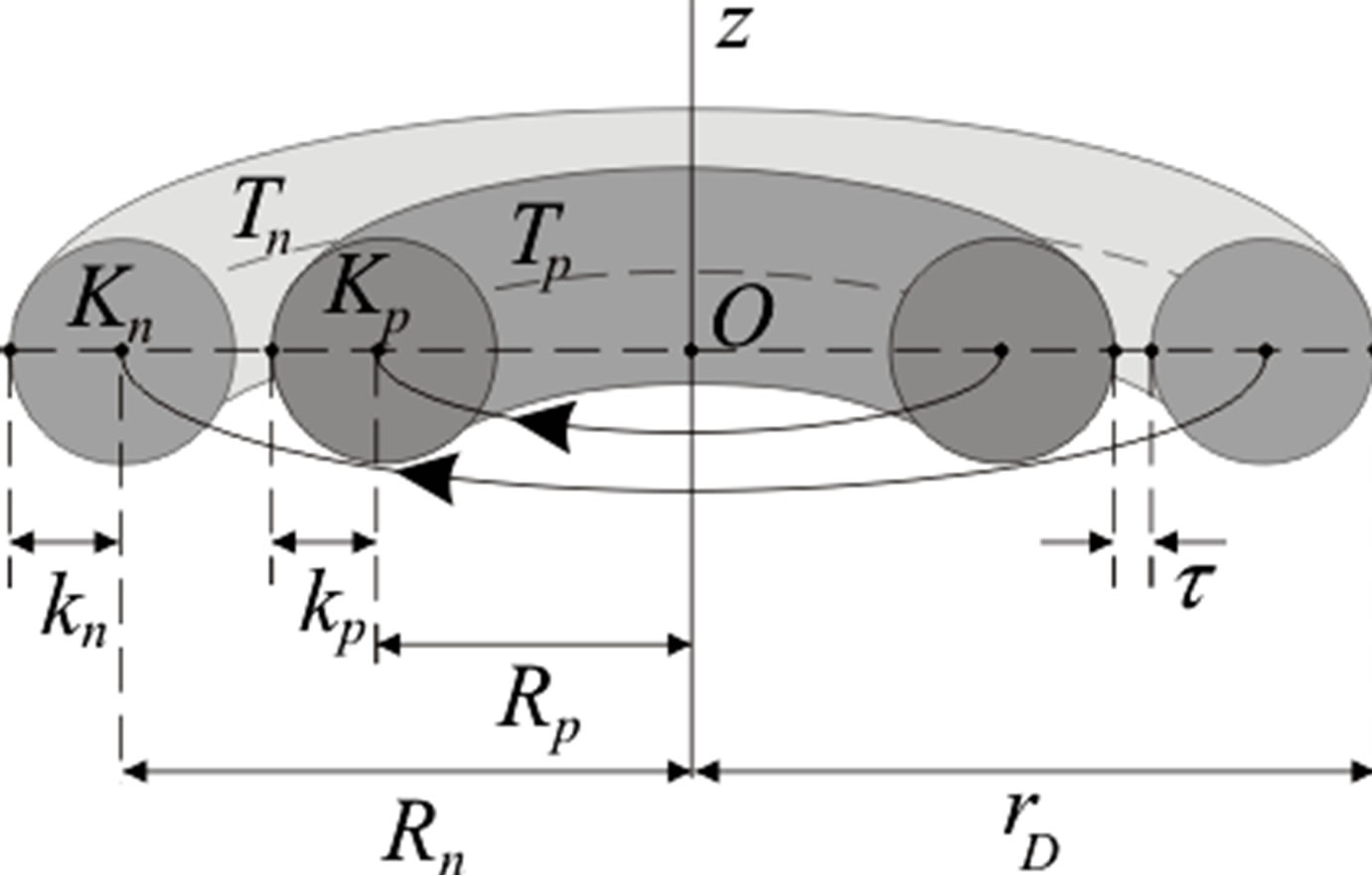
Figure 4. Cross-section of the model of the deuteron.
From this structure follows that the spin  of the deuteron will be a sum of the spins
of the deuteron will be a sum of the spins  of the proton and neutron, i.e. the spin of the deuteron is
of the proton and neutron, i.e. the spin of the deuteron is , which has been experimentally obtained.
, which has been experimentally obtained.
The nucleons, binding to each other within the deuteron almost double their total mass relative to their separate masses and as a consequence the centrifugal force increases. From this follows that the radius of the deuteron is larger than the radii of the nucleons and as has been experimentally determined it is  m [18].
m [18].
Let us assume that the charge of each of the nucleons is distributed parallel along a circle with a center O. Then a circular current appears and the magnetic moments of the nucleons are proportional to the magnitude of the charges and their angular velocity but also to the square of their distance from the center of rotation. The inlaying of the proton within the neutron increases the radius of the neutron more relative to the increased radius of the proton. This explains why the sum of the magnetic moments of the proton  JT–1 and neutron
JT–1 and neutron  JT–1 is larger than the magnetic moment of the deuteron
JT–1 is larger than the magnetic moment of the deuteron
 JT–1 [18].
JT–1 [18].
Let  and
and  be the centers of the forming circles of
be the centers of the forming circles of  and
and  and let the radii of those circles be
and let the radii of those circles be  and
and 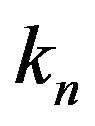 correspondingly. We denote as
correspondingly. We denote as  and
and  the radii of the central circles of the tori
the radii of the central circles of the tori  and
and  (Figure 4).
(Figure 4).
In this case  and
and , also
, also  and
and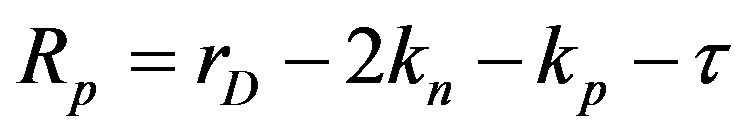 . Based on the method we described in Section 3 using mass volume density
. Based on the method we described in Section 3 using mass volume density  of the nucleons from Table 1 we find
of the nucleons from Table 1 we find ,
, 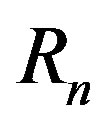 ,
,  and
and . In formula (12) we consider the mass defect, proportionally for the masses of the proton and neutron. The experimentally obtained mass of the deuteron is
. In formula (12) we consider the mass defect, proportionally for the masses of the proton and neutron. The experimentally obtained mass of the deuteron is  kg [18]. Then, according to formula (20), the binding energy of the deuteron is
kg [18]. Then, according to formula (20), the binding energy of the deuteron is  J.
J.
This value we confirm at different values of the distance 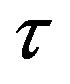 between the tori (Table 2) for
between the tori (Table 2) for  with the corresponding formula from (19). From (19) we also obtain the force of interaction
with the corresponding formula from (19). From (19) we also obtain the force of interaction  for the deuteron.
for the deuteron.
In Table 2 we have denoted with  and
and  respectively the radius of the forming circle of the torus of the neutron and the proton, with
respectively the radius of the forming circle of the torus of the neutron and the proton, with  and
and  respecttively the radius of the central circle of the torus of the neutron and the proton and with
respecttively the radius of the central circle of the torus of the neutron and the proton and with  the force of interaction between the nucleons in the deuteron.
the force of interaction between the nucleons in the deuteron.
5. MODEL OF THE TRITON
The triton is obtained structurally from the deuteron by adding one more neutron. The second neutron tries to take over the place of the first one.
The neutron, although it can be assumed electrically neutral, i.e. with a common charge n = 0, has an internal electric structure, its negative charge, as opposed to the positive one is distributed primarily at its surface [20,21].
Then because of the repulsion between the tori  and
and  the central circles of the nucleons will be situated symmetrically in two planes parallel to the plane in which the central circle of proton torus
the central circles of the nucleons will be situated symmetrically in two planes parallel to the plane in which the central circle of proton torus  is situated. At that
is situated. At that  and
and  will be at the same distance
will be at the same distance  m from
m from . This configuration provides symmetry relative to the center of masses (geometrical center) O of the triton (Figure 5). From this follows the relative stability of the triton
. This configuration provides symmetry relative to the center of masses (geometrical center) O of the triton (Figure 5). From this follows the relative stability of the triton  y.
y.
Let us denote as  the centers of the tori
the centers of the tori 
 and as
and as —the center of
—the center of . Then the center
. Then the center 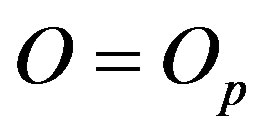 and the points
and the points  are on the same line z, perpendicular to their plane of rotation.
are on the same line z, perpendicular to their plane of rotation.
The tori  and
and  rotate around z with a constant angular velocity
rotate around z with a constant angular velocity  in the same direction (e.g. clockwise) and
in the same direction (e.g. clockwise) and  will rotate with the same velocity in the opposite direction (counterclockwise), i.e. with a velocity
will rotate with the same velocity in the opposite direction (counterclockwise), i.e. with a velocity . Thus we obtain that the spin of the triton is
. Thus we obtain that the spin of the triton is 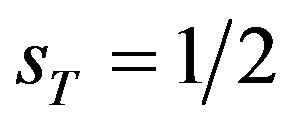 which is experimentally confirmed.
which is experimentally confirmed.
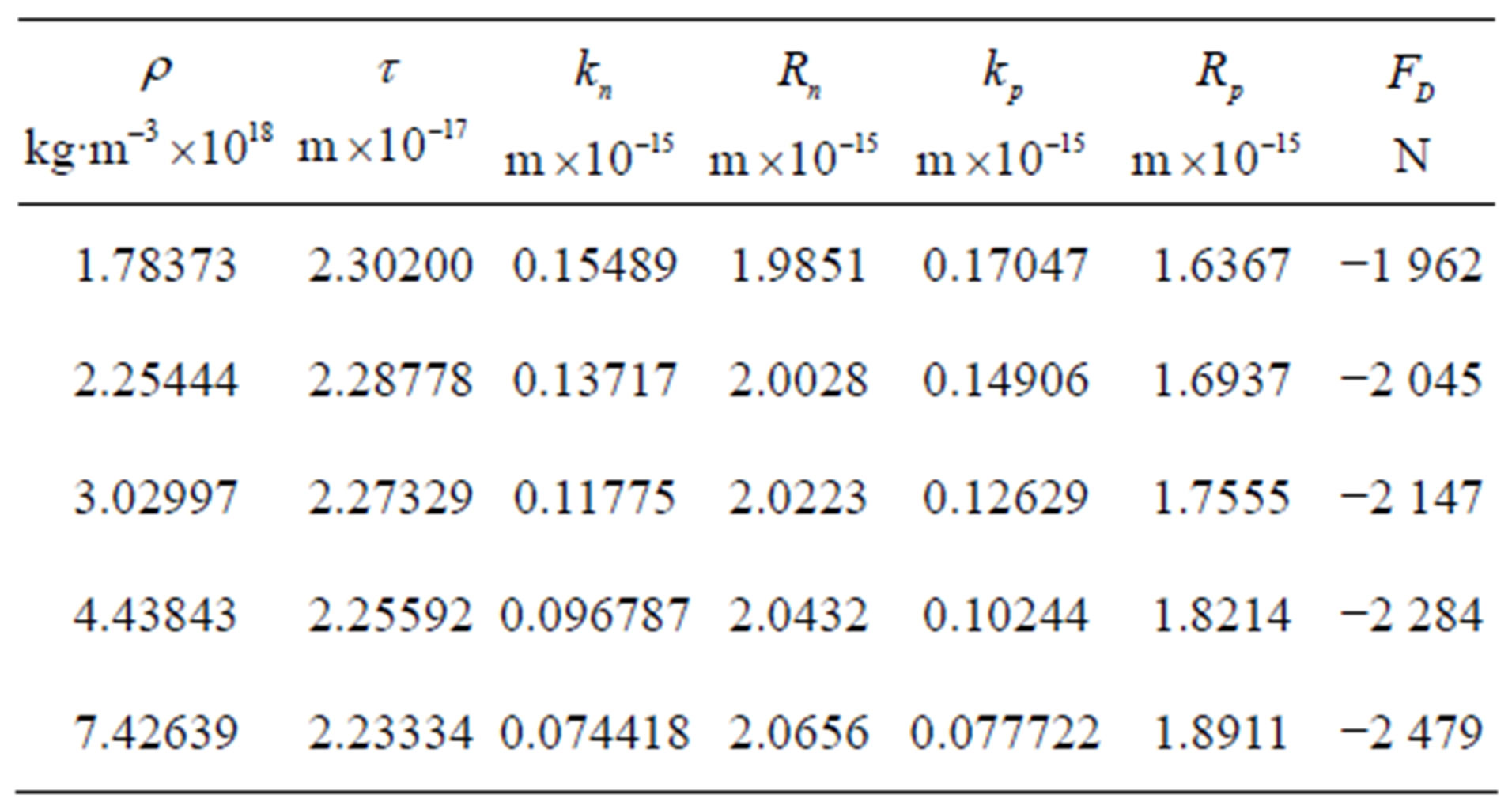
Table 2. Size of the nucleons and force of interaction in the deuteron.
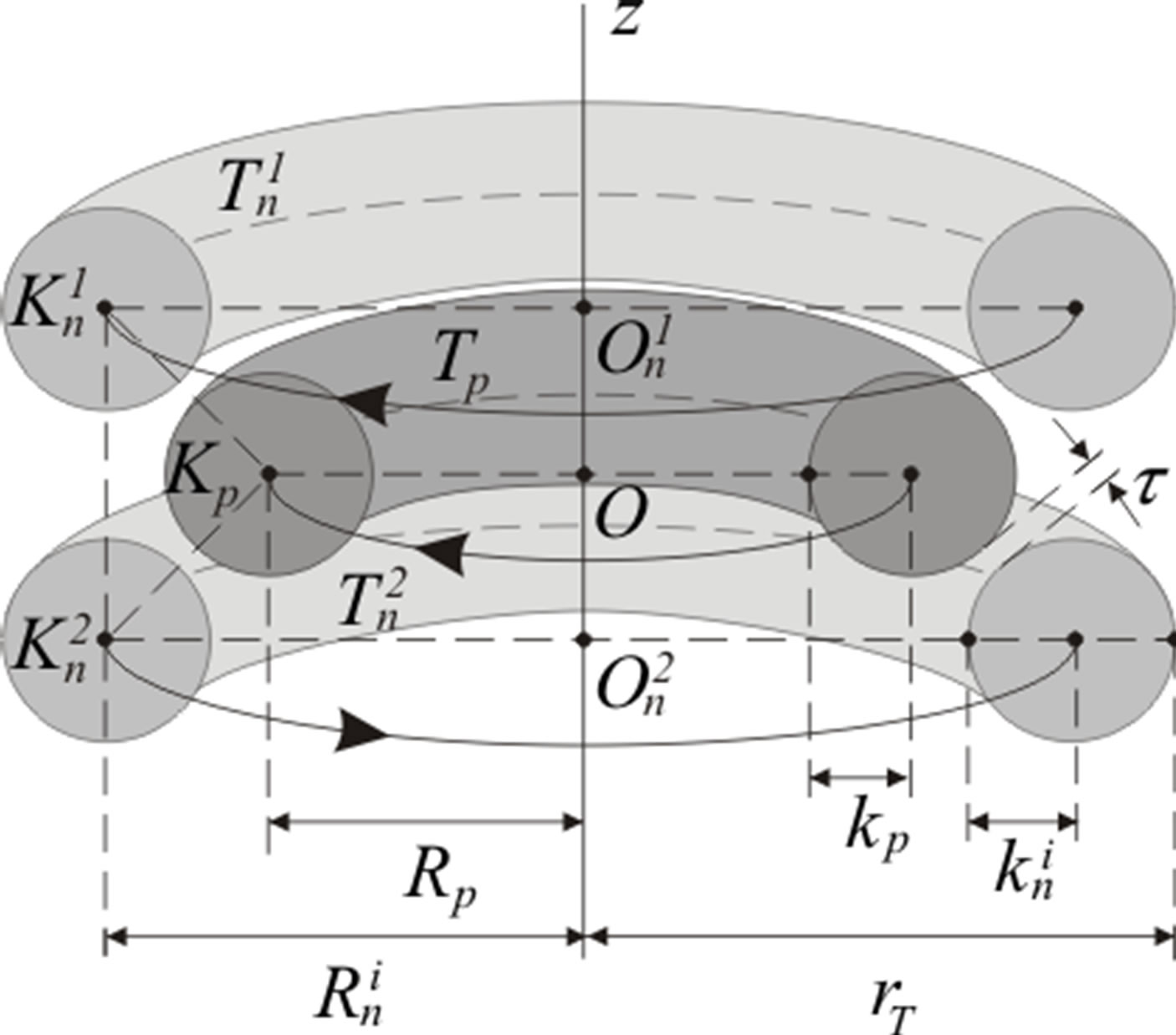
Figure 5. Cross-section of the model of the triton.
The neutron that rotates in an opposite direction will decrease the centrifugal force caused by the nucleons rotating in the same direction. Therefore the radius of the triton . According to experiments
. According to experiments  m [22].
m [22].
The magnetic moments caused by the redistributed charges in the neutrons cancel each other out. Thus the magnetic moment of the triton is caused only by the charge of the proton. As a consequence of the increased radius of the proton relative to the free state the magnetic moment of the triton  JT–1 is larger than the magnetic moment of the proton
JT–1 is larger than the magnetic moment of the proton  JT–1, as shown by experimental data [18].
JT–1, as shown by experimental data [18].
Let 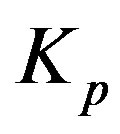 and
and 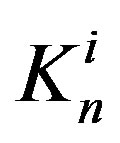 be the centers of the forming circles respectively of
be the centers of the forming circles respectively of  and
and 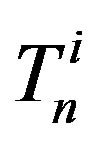 with corresponding radii
with corresponding radii  and
and 
 . We denote
. We denote  and for
and for ,
, .
.
In this case  and if
and if 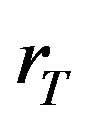 is the radius of the triton, then
is the radius of the triton, then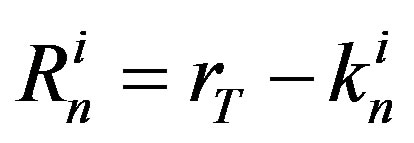 .
.
Due to the central symmetry of the charge of the proton we can assume that all of its charge  is concentrated in the geometrical center O. Because of that we model the proton as a sphere
is concentrated in the geometrical center O. Because of that we model the proton as a sphere  with a center O and radius
with a center O and radius , equivalent in surface are to
, equivalent in surface are to . At that
. At that 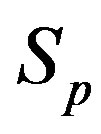 is charged with a charge
is charged with a charge , which is centrally symmetrical and can be redistributed.
, which is centrally symmetrical and can be redistributed.
With  (
( ) we denote the tori that are equivalent in surface to
) we denote the tori that are equivalent in surface to  with centers
with centers  and centers of the forming circles
and centers of the forming circles  (Figure 6). At that
(Figure 6). At that  and
and 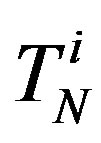 have the same distance
have the same distance 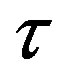 between them as
between them as  and
and . With
. With 
 we denoted the forming sphere of
we denoted the forming sphere of .
.
We assume the point O to be stationary relative to the inertial reference frame J. We introduce two solid noninertial reference systems  and
and , that rotate with the constant angular velocities
, that rotate with the constant angular velocities  and
and 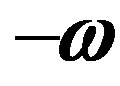 respectively of
respectively of 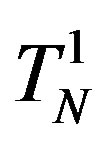 and
and  relative to J.
relative to J.
The point O is a center of the coordinate system  stationary connected with the reference system
stationary connected with the reference system 
 relative to which the spheres
relative to which the spheres  and
and  are stationary to each other (Figure 6).
are stationary to each other (Figure 6).
The two tori 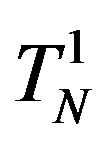 and
and  are symmetrical relative to the sphere
are symmetrical relative to the sphere . Then it is enough to study the electrostatic interaction only between one of them and
. Then it is enough to study the electrostatic interaction only between one of them and . We assume with some approximation that between
. We assume with some approximation that between  and
and 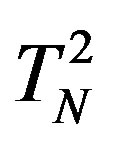 there is no electrostatic interaction since their total charges are zero. Besides that, to simplify the calculations, we assume that the distance between the surfaces of each of the tori is the same and equal to
there is no electrostatic interaction since their total charges are zero. Besides that, to simplify the calculations, we assume that the distance between the surfaces of each of the tori is the same and equal to . Then the distance
. Then the distance .
.
Since , using the model we revealed in Section 3, with the volume mass density
, using the model we revealed in Section 3, with the volume mass density  of the nucleons from Table 1 we find
of the nucleons from Table 1 we find ,
,  and
and ,
,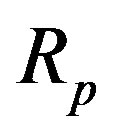 . In formula (12) we consider the mass defect proportionally for the masses of the proton and two neutrons. The experimenttally obtained mass of the triton is
. In formula (12) we consider the mass defect proportionally for the masses of the proton and two neutrons. The experimenttally obtained mass of the triton is  kg [18].
kg [18].
Then, according to formula (20) the binding energy of the triton is  J. This value we confirm for different values of the distance
J. This value we confirm for different values of the distance  between the tori (Table 3) for
between the tori (Table 3) for ,
,  or
or  using the corresponding formula from (19). From (19) we also obtain the force of interaction for the triton
using the corresponding formula from (19). From (19) we also obtain the force of interaction for the triton  for
for  or
or .
.
In Table 3 we have denoted with  and
and 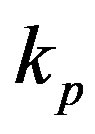 respectively the radius of the forming circle of the torus of the neutron and the proton, with
respectively the radius of the forming circle of the torus of the neutron and the proton, with  and
and  respectively the radius of the central circle of the torus of the neutron and the proton and with
respectively the radius of the central circle of the torus of the neutron and the proton and with  the force of interaction between the nucleons in the triton.
the force of interaction between the nucleons in the triton.
We should note that by determining the value of , we can also vary h, where in this case is fulfilled
, we can also vary h, where in this case is fulfilled  .
.
6. DISCUSSION
In [12] considering the nucleons as tori we theoreticcally determine the potential energy and the force of interaction in the systems: proton-neutron, proton-proton and proton-neutron-proton, which we derive using experimentally obtained results for the radii and the masses of the nucleons in unbound condition.
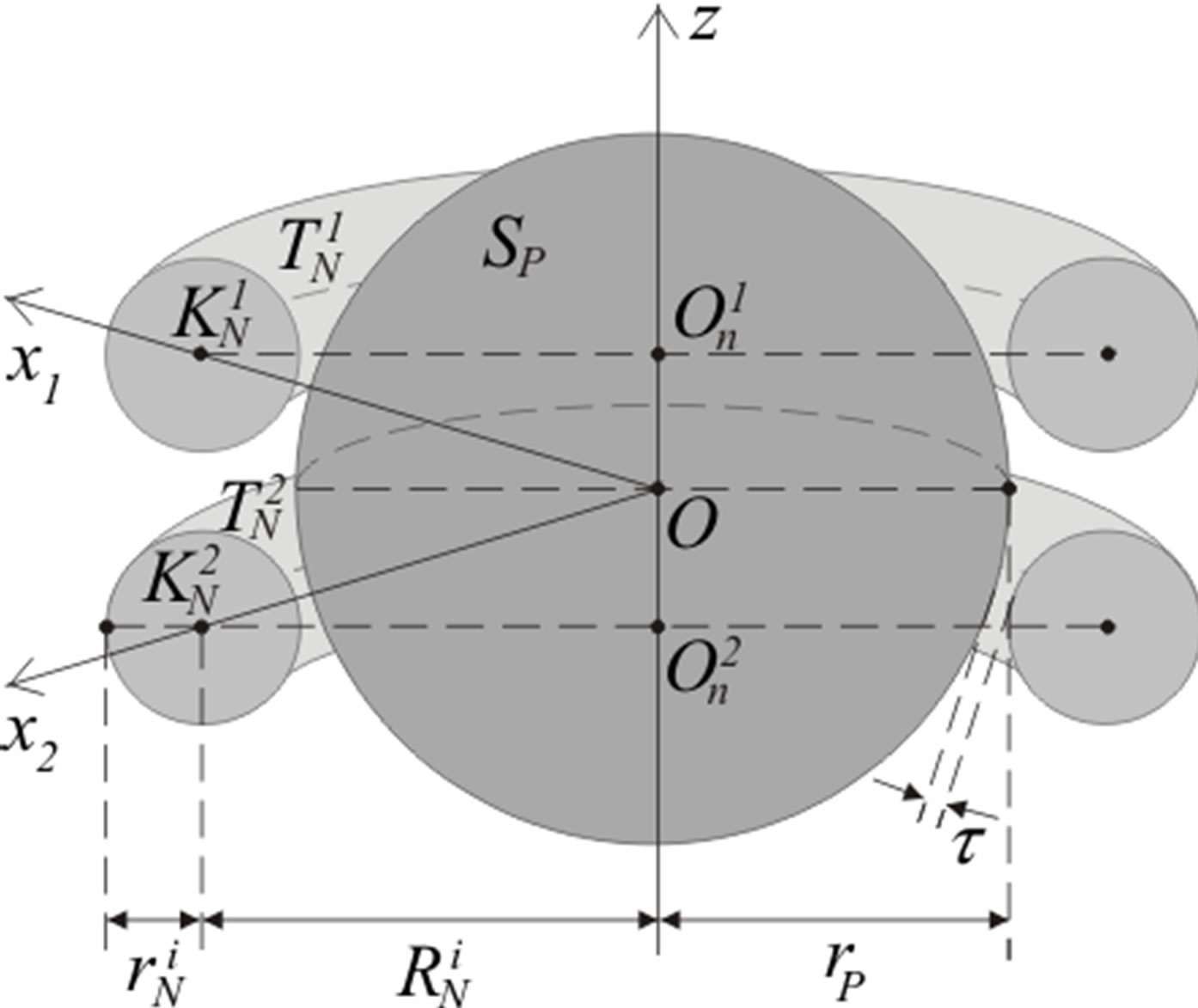
Figure 6. Cross-section of the reduced model of the triton.
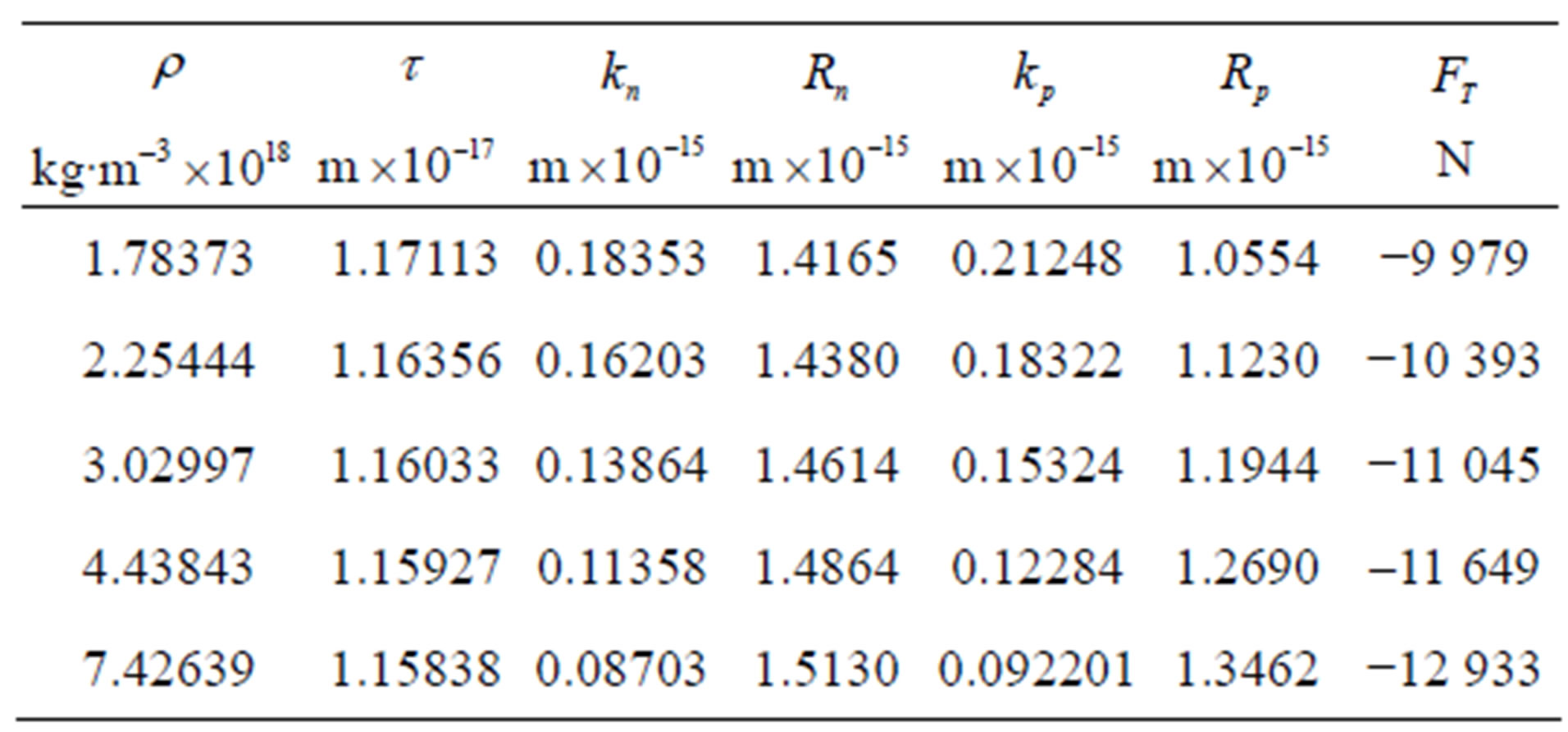
Table 3. Size of the nucleons and force of interaction in the triton.
Using our method, we have shown that the electromagnetic forces for the proton-neutron pair are quite strong (in the order of the nuclear forces) an short-ranged. This suggests that the binding energy of the nucleons have electromagnetic nature. We can also explain other basic experimental data like stability, radius, magnetic moment and spin of the nuclei.
In this paper, we concretize the general results obtained in [12] for the nuclei of deuterium and tritium.
7. CONCLUSIONS
Nuclear physics bases its knowledge on experiments and has numerous different contradicting models. Considering nucleons as tori and modeling the deuteron and triton, we obtain and explain their basic experimentally obtained characteristics and also obtain new characteristics of these nuclei.
Our model can also be applied for more complicated atomic nuclei. Based on particular charge and current configurations to it can be considered the interaction betweennucleons in electrodynamic aspect; to be find analytical expressions for the magnetic moments, to determine the angular velocity of nucleons, the linear velocity at particular points on their surface, etc.; to explain excited states of the nuclei; to be find out the potential of the electromagnetic field generated by atomic nuclei and to calculate their quadrupole moments for the deuteron and the other nuclei.
8. ACKNOWLEDGEMENTS
The authors express their gratitude to the computer specialist Stefan Bozhkov, who with the help of Wolfram Mathematica 7.0 performs the calculations in this article. The results of the present studies are published with the financial support of the Fund for Scientific Research with the Ministry of Education and Science under contract DTC No. 02/35.