1. Introduction
Renormalization theory is related to some unsolved problems about the Mandelbrot set
, such as the self-similarity and the local connectedness conjecture [1] . Some of the most important renormalization theories are: quadratic-like (or Douady-Hubbard) [2] [3] , parabolic [4] , and Siegel [5] [6] .
Our work focuses on the renormalization of Siegel-type functions, that is, holomorphic functions
with an indifferent fixed point α, which has a neighborhood where it is linearizable, it means that is conjugated to a rotation, of an irrational angle
, on the unit disk. Its maximal domain of linearization Zf is called the Siegel disk of f. We are assuming f has a unique critical point which is located in the quasicircle
, so by ( [7] , Theorem 3.2), θ has a (simple) continued fraction, where all the elements of the continued fraction are bounded.
One of the most important works about the renormalization of Siegel-type functions is that of McMullen [5] where he works with holomorphic pairs which are intended to complexify analytic commuting pairs, that is, the dynamic behavior on the boundary of the Siegel disk near the critical point. This renormalization relates the approximation in continued fraction of a number θ with the first return maps of the rotation by an angle θ at intervals on the boundary of the unit disk. When he applies these tools to a quadratic polynomial with rotation number with periodic continued fraction, he showed that the renormalizations converge to a fixed point geometrically fast, leading to an insight of the hyperbolicity for these parameters.
Later, Yampolsky [6] introduced the cylindrical renormalization and using the results of the McMullen Siegel renormalization, constructs hyperbolic fixed points for this operator and proves that the dimension of its unstable manifold is exactly one.
On the other hand in [8] , Branner and Douady defined a type of surgery that embeds the basilica limb-1/2 onto the rabbit limb-1/3, which consists of removing certain sectors of the Julia sets of parameters in the limb-1/3 to obtain Julia sets of parameters in the limb-1/2, and vice versa, for the parameters in the limb-1/2 they add the copy of certain sectors of their Julia set to obtain Julia sets of parameters in the limb-1/3.
Using the previous concepts in [7] they defined a new type of renormalization, called the Pacman renormalization. For this, Pacman-type functions are introduced (Definition 1), which are holomorphic functions
between two nested domains such that
is a double-branched covering where
is an arc connecting α with
(Figure 1).
![]()
Figure 1. On the left side we see a full-Pacman
, which is a two-to-one analytic function from
to
and such that
. A Pacman
which is the truncated version of a full Pacman with
is shown on the right.
To define the general Pacman renormalization they first define the prime Pacman renormalization of a full Pacman f ( [7] , p.11). In a few words the sector S1, bounded by a curve
and its image
, its removed by gluing
and
along
, and then taking the first return map to the complement of the sector S1, so we get a new full-Pacman.
They define a pre-renormalization as a prepacman (Definition 3), which is a piecewise holomorphic function defined on a sector with two branches; one branch is univalent while the other branch has a single critical point and a small sector anchored to the other preimage of the fixed point α. Thus the prepacman is obtained as the first return maps to a sector S anchored to the fixed point. Then the sector S is glued properly and with it we obtain an abstract Pacman that finally embeds to the complex plane.
The general Pacman renormalization of a Pacman f exists if there is a prepacman defined in a sector S anchored to the fixed point α and such that the functions of the prepacman are iterates of f realizing the first return map to S (Definition 4). The Pacman renormalization is combinatorially some iteration of the prime Pacman renormalization. This type of renormalization is mainly used in Siegel pacmen (Definition 8), which are pacmen functions that have a neighborhood centered on the fixed point α where they are Siegel maps. Although to apply this operator it is not necessary for the function to be a Pacman, it is enough that exists a prepacman in the dynamic plane of an analytic function with distinguished fixed point α, so that a compact and analytic Pacman renormalization operator can be defined near it (Remark 1).
In ( [7] , Theorem 1.1), they proved that for any rotation number θ with periodic continued fraction expansion (Definition 6), the Pacman renormalization operator has a unique periodic point
which is a Siegel Pacman with rotation number θ. Furthermore this periodic point is hyperbolic with one-dimensional unstable manifold and the stable manifold consist of all Siegel Pacman with the same rotation number. By applying the Pacman renormalization operator to the quadratic Siegel polynomials on the main cardioid of the Mandelbrot set, with periodic rotation number, they were able to get rescaling coefficients for the centers of the small satellite copies of the Mandelbrot set close to these Siegel parameters of periodic type.
The main motivation of this work was to extend the previous result ( [7] , Theorem 1.1) to Siegel parameters of bounded type but to achieve this it is necessary to build a renormalization horseshoe for this Pacman renormalization operator. In the first Theorem of this article we prove that, due to the results in [7] , for any Siegel Pacman (or Siegel map), with combinatorially bounded rotation number (Definition 6), there is some neighborhood where the Pacman renormalization operator is compact and analytic, in addition it acts on the rotation number as some iteration of the function Rprm (Lemma 4).
Theorem 1. For any Siegel Pacman (or Siegel map)
with rotation number
, there exists a Siegel prepacman
around any point
, different from the critical point or any of his iterated preimges, and a gluing function
that projects F to the Siegel Pacman
with rotation number
, for some
. Also there exists small Banach neighborhoods
and
and a Pacman renormalization operator
such that
is compact and analytic.
It is worth mentioning that when the rotation number is combinatorially periodic (Definition 6) the Pacman renormalization operator is not necessarily the same as ( [7] , Theorem 3.16), because they build a very specific sector of renormalization that they need for the operator to fix a Siegel Pacman with periodic rotation number.
Due to Theorem 1 we were able to define a Pacman renormalization operator
for which we built a horseshoe, for this we need to focus on a specific type of Siegel pacmen, the standard Siegel pacmen (Definition 10), because we can work with their hybrid classes (Remark 2). First given a fixed
, we define the set of irrational rotation numbers
(Definition 11), such that their continued fraction (Definition 5) satisfies that all their elements are bounded by M. With this we can define the horseshoe or the non-escape set
(Definition 11), which will be the set of hybrid classes of standard Siegel pacmen with rotation numbers in
, these classes are infinitely renormalizable backwards and forwards under the renormalization operator
(Definition 11), where renormalizing a hybrid class means to apply the Pacman renormalization operator
to one representative of the hybrid class, this is well defined because of Theorem 1. The operator
acts on the rotation numbers as the function Rprm iterated a number of times such that it eliminates the first element of the continued fraction of the angle. For the conjugation we consider the space
of bi-infinite sequences of natural numbers bounded by the constant M, with the weak topology (Definition 12). The left shift
move each element of the sequence one space to the left (Definition 12). We prove the following theorem in a similar way as Lyubich proves ( [3] , Lemma 8.1), but instead of asking the a priori bounds condition, we used that the set
is closed (Remark 4).
Theorem 2. For any
the set
is a horseshoe for the renormalization operator
which acts on the standard Siegel pacmen classes with rotation number in
. The natural extension
is a homeomorphism topologically conjugated to the left shift
while
is semiconjugate to ω.
To show that the set
is a horseshoe for the renormalization operator
we need to prove that any element of the set
has bi-infinite and precompact orbits with respect to the Pacman renormalization operator
and also that this renormalization operator is topologically semiconjugate to the left shift in the space
with the weak topology.
The contribution of this work is bring us a few steps closer to the Lyubich conjecture ( [7] , Appendix C) that it can be defined a global Pacman renormalization operator on the main molecule of the Mandelbrot set which will be hyperbolic with one dimensional unstable manifold such that its renormalization horseshoe is compact and combinatorially related with Rprm, which would imply MLC for any parameter in the main molecule.
2. Preliminaries
Most of the definitions in this section are due to [7] . For technical reasons in the Pacman renormalization theory, two types of pacmen functions are used: full-pacmen and truncated pacmen or simply pacmen. A Pacman is obtained from a full-Pacman by removing a small neighborhood of the pre-fixed point α’ (the other perimage of the fixed point α). On the other hand we can get a full-Pacman from a truncated Pacman by extending it topologically.
Definition 1. Consider a closed topological disk
with a simple arc
, connecting a boundary point of V to a point α in the interior. A full-Pacman is a map
such that:
• α is a fixed point of f:
.
•
is a closed topological disk.
• The critical arc
has exactly three lifts:
and
, such that
starts at the fixed point α while
start at the pre-fixed point α’; we assume that
only intersect
in α.
•
is analytic and
is a two-to-one branched covering. Whence f has only one critical point
. We denote by
the critical value of f.
• f admits a locally conformal extension through
.
Let O be a small closed topological disk around α such that
and suppose that
cross-intersects
at a single point. There are two connected components
and
of
. Removing
from the domain U, we get a truncated Pacman or simply Pacman
This truncated Pacman is an analytic function admitting a locally conformal extension through
such that it can be topologically extended to a full Pacman.
We consider two subsets of
: the external boundary
and the forbidden part of the boundary
(Figure 1).
Note that full-pacmen functions are almost quadratic-like functions [2] , the problem is the curve
since it has three preimages and also makes that
.
We can get some examples of full Pacman and Pacman functions applying the Pacman renormalization to any Siegel function like a Siegel polynomial ( [7] , Lemma 3.4).
For a Pacman
, the non-escaping set
can be defined in a similar way as it defined for quadratic like functions ( [3] , p. 332), as the intersection of all preimages of f, and the escaping set is the complement
.
External rays of a Pacman can be defined embedding a rectangle
in
so that the base
of the rectangle is
and the top horizontal side
is a subset of
. The images of the vertical lines whithin
form a lamination of
. We pullback this lamination to all iterated preimages
. The leaves of this lamination that begins at
are called external rays segments; an infinite ray segment is called external ray. We can also define the angle
of the external ray segment passing through a point a in a subset
( [7] , pp. 10-11).
The objects required to accomplish Pacman renormalization are then defined. This process takes place in a sector, which is a subset of the Pacman domain, and is pasted topologically with a function to produce another Pacman.
Definition 2. A sector S is a closed topological disk with two distinguished arcs
meeting at a single point, called the vertex of S. A gluing is a map
from a closed sector
onto a closed topological disk
in such a way that the function
is conformal in the interior of S,
and
can be conformally extended to a neighborhood of any point in
except at the vertex of S.
The following definition of prepacman is the analogue of McMullen’s holomorphic pairs ( [6] , Definition 2.3).
Definition 3. Consider a closed sector
divided in two subsectors
by the interior ray
. Let
,
be a pair of holomorphic maps, defined on
,
. We say that
is a prepacman if there exists a gluing
on S which projects
onto a (full)-Pacman
where
are mapped to the critical arc
and
is mapped to
(Figure 2). The map
is called a renormalization change of variables. The dynamical objects like the non-escaping set of a prepacman F are preimages contained in S of the corresponding dynamical objects of f under
.
Since each of
and
has two preimages, one of which is
, then the gluing makes
to have exactly three preimages. Also the definition implies that
commute in a neighborhood of
.
We will see later that the following Pacman renormalization definition can be extended to any function
with a distinguished fixed point
, that is, the Pacman renormalization is not only defined for Pacman functions but for any function that has a prepacman, such as any Siegel function ( [7] , Corollary 3.7).
Definition 4. A (full)-Pacman
is renormalizable if there exist a prepacman
![]()
Figure 2. In a (full)-prepacman (
,
) we have
, where the critical point of
belongs to
so
maps
two-to-one to
and
one-to-one to
. The function
maps
univalently onto
. After gluing the sector with
,
,
,
, we obtain a full-Pacman.
defined on a sector
with vertex at α, such that
are iterates of f realizing the first return map to S and such that the f-orbits of
, before they return to S, cover a neighborhood of α compactly contained in U. We said that F is the pre-renormalization of f and the Pacman
the renormalization of f.
Note that by ( [7] , Lemma A.2), the Pacman renormalization comes from a sector renormalization on the closed unit disk, then combinatorially any Pacman renormalization is some iteration of the prime Pacman renormalization.
To give a Banach space structure to the space of pacmen functions they use the uniform norm in the space of analytic functions. So if
is a Pacman with a truncation disk
and assuming that there is a topological disk
with a piecewise smooth boundary such that f extends analytically to W and continuously to its closure. For any small
, a Banach ball
is the set of analytic maps
with continuous extensions to
such that
Next it is shown that the Pacman renormalization operator is analytic in a Banach ball, which means that it is Frechet differentiable on these Banach spaces, and the differential is linear with respect to the complex numbers.
We say that a curve γ lands at α, at a well-defined angle, if there exists a tangent line to γ at α. Due to ( [7] , Lemma 2.5) we know that given a Pacman
, it is enough that the curves
and
land at well-defined angles for the existance of a small Banach neighborhood
of f where all the maps
have a domain
, such that
is a Pacman with the same
but translated to the point
, the fixed point of g. Furthermore, periodic rays are also stable, that is, if a periodic ray
of f lands at a repelling periodic point
, then the periodic ray
of g lands at
and
is contained in a small neighborhood of
.
Now suppose that f has a renormalization sector Sf, using the above and solving the Beltrami equation for the push forward of the Beltrami differential generated by a holomorphic movement of the sector Sf (the prepacman of f), renormalization sectors Sg and gluing functions
are obtained that depend analytically of g in a small enough Banach neighborhood of f. That is, once we know that there is a renormalization sector Sf for f whose curves
land in α with a well-defined angle, then there is also a prepacman for the functions g in a sufficiently small neighborhood of f and therefore they will also be Pacman renormalizable. That is how they get the following result ( [7] , Theorem 2.7), which states that in order to obtain a compact and analytic Pacman renormalization operator, it is sufficient for a prepacman of f to exist with curves landing at well-defined angles on
.
Theorem 3 Set
a Pacman and
its renormalization. Suppose that the curves
land at α at pairwise distinct well-defined angles. Then for every sufficiently small ε, it is defined in the neighborhood
a compact analytic Pacman renormalization operator
such that
.
Remark 1. It is important to note that the proof of the previously stated theorem does not require that the function f be a Pacman, rather it only requires that a prepacman can be defined in the dynamic plane of an analytic map f with a fixed point α. This allows us to define a compact analytic Pacman renormalization operator near f.
Now we are going to define the continued fraction representation of a number [5] [9] , it is related with the approximation of irrational numbers ( [10] , Appendix C), the linealization of Siegel maps ( [10] , Chapter 11) and to know how the rotation number changes when the Pacman renormalization is applied ( [7] , Lemma 3.4).
Definition 5. A (simple) continued fraction is an expression of the form:
where
and
, for all
, are called coefficients or terms of the continued fraction.
Due to a result of Euler ( [9] , p. 177), every real number α can be represented uniquely by a (simple) continued fraction, this continued fraction is finite if α is rational and infinite if α is irrational (the rational numbers may have two representations because
).
Definition 6. Denote
the set of combinatorially periodic rotation numbers, that is, the numbers
with periodic continued fraction (with periodicity begining at a1), so it has a block of elements
that are repeated periodically and written:
Denote
the set of combinatorially bounded rotation numbers, that is, the numbers
with the elements of its continued fraction bounded by the same constant:
Observe that
.
Next we define a Siegel map with only one critical point, these are the function where we are interested in applying the Pacman renormalization.
Definition 7. Set a holomorphic map
which has an indifferent fixed point α with multiplier
and rotation number
that is locally linearizable in a neighborhood of α, it means that is topologically conjugated to the rotation
in the unit disk. Its maximal completely invariant linearization domain
is called the Siegel disk of f. If
is a quasidisk whose boundary contains exactly one critical point
, then f is called a (unicritical) Siegel map. There is a foliation of the Siegel disk
of f by equipotentials that come from the linearization, parametrized by their heights ranging from 0 (the height of α) to 1 (the height of
).
For example if a quadratic polynomial of the form
has an indifferent fixed point on
with multiplier
and rotation number
, then by ( [7] , Theorem 3.2), it is a Siegel map and
is located in the main cardioid of the Mandelbrot set.
Definition 8. A Pacman
is Siegel if:
1) f is a Siegel map with Siegel disk
centered at α.
2) The critical arc
is the concatenation of an external ray R1 with an inner ray I1, such that the unique point in the intersection
is not precritical.
3) The truncated Pacman is
, where
.
The rotation number and multiplier of a Siegel Pacman are identical to those of a Siegel map (Definition 7). By ( [7] , Theorem 3.2), it follows that the rotation number of a Siegel map is in
. The level of truncation of f is the height of
. The Julia set of the Siegel Pacman f is:
.
Since
is a concatenation of rays, then
is a concatenation of an external ray R0 and an internal ray I0 with
. We said that two Siegel pacmen f and g are combinatorially equivalent if they have the same rotation number and if
and
have the same external angles.
The prime Pacman renormalization ( [7] , p.11) is a suitable extension of the prime renormalization of a rotation on the closed unit disk
( [7] , Appendix A). It involves the removing of a sector
based on the fisrt return map to the complement
. We get a new rotation on the closed unit disk by gluing this complement by a function that depends on the rotation number, so it is enough to know how this gluing function acts on the rotation numbers to know how the prime Pacman renormalization change the rotation number of a Siegel Pacman ( [7] , Lemma A.1).
Lemma 4. The rotation number of the prime renormalization of a rotation
by an angle θ is:
If the continued fraction of θ is
with
, then
Observe that
if and only if there exists
such that
.
Since the Pacman renormalization is an extension of the sector renormalization on the unit disk which in turn is some iteration of the prime renormalization of a rotation on the unit disk ( [7] , Lemma A.2), then the Pacman renormalization also acts on the rotation numbers as some iteration of the above function Rprm ( [7] , Lemma 3.4).
Definition 9. A hybrid conjugacy between Siegel maps
and
is a quasiconformal conjugacy
that is conformal on the Siegel disks. A hybrid conjugacy between Siegel pacmen is defined analogously.
The hybrid conjugacy relation between Siegel maps (pacmen) on their Siegel disk, tells us that these functions have essentially the same dynamics on their Julia sets, because we can get all the Julia set by just taking the preimages of the Siegel disk. The hybrid conjugacy is an equivalence relation so we can work with hybrid classes.
Now we mention some of the results in ( [7] , pp. 16-29), that we are going to use in the proof of the Theorem 1.
According to ( [7] , Theorem 3.6), a Siegel map’s rotation number determines its hybrid class on a neighborhood of the Siegel disk. However, for two Siegel pacmen, which are combinatorially equivalent, to be hybrid equivalent on their respective domains, they must also have the same truncation level ( [7] , Theorem 3.11).
A Siegel prepacman F is just a prepacman of a Siegel Pacman f (Definition 3), but now to work with hybrid classes we are also going to care about the point at which the curve
of the sector of the prepacman intersects with the Siegel disc of f. We say that f has a prepacman F around
if
intersects
at x.
One of the first important results in [7] is the Lemma 3.4, it tell us that given any Siegel quadratic polynomial with rotation number of bounded type, there exists a prepacman around any point
which is neither the critical point nor its iterated preimage, that makes it Pacman renormalizable. Also the rotation number changes as some iteration of the function Rprm and the spreading of
around α stays as close as we want to the Siegel disk. Using this and ( [7] , Theorem 3.6), we can send a prepacman of any Siegel quadratic polynomial to a prepacman of any Siegel function with the same rotation number as the polynomial, so every Siegel map is Pacman renormalizable ( [7] , Corollary 3.7).
Definition 10. A standard Siegel Pacman ( [7] , p. 26), is just a Siegel Pacman with
passing through the critical value and a standard prepacman is just a prepacman around the critical value in the dynamical plane of a Siegel map.
The next remark tell us that, after setting a level of truncation, we can work with the hybrid Siegel pacmen classes, which are determined by their rotation number.
Remark 2. By ( [7] , Theorem 3.11), we know that two standard Siegel Pacman (with the same truncation level) are hybrid equivalent if and only if they have the same rotation number.
3. Main Results
In this section we are going to prove Therorem 1 and Therorem 2 from the introduction.
Theorem 1 follows from the results in [7] and tells us that for any Siegel Pacman (or Siegel map), with combinatorially bounded rotation number, there is some neighborhood where the Pacman renormalization operator is analytic and compact.
Theorem 5. For any Siegel Pacman (or Siegel map)
with rotation number
, there exists a Siegel prepacman
around any point
, different from the critical point or any of his iterated preimges, and a gluing function
that projects F to the Siegel Pacman
with rotation number
, for some
. Also there exists small Banach neighborhoods
and
and a Pacman renormalization operator
such that
is compact and analytic.
Proof. We know that every Siegel map is Pacman renormalizable ( [7] , Corollary 3.7), in particular if the rotation number θ of f is of bounded type ( [7] , Lemma 3.4). Then we can use Theorem 3, so there is a neighborhood of f small enough where we can define a Pacman renormalization operator that is compact and analytic. 
Note that the renormalization sector of f in the last theorem when x is the critical value
and the rotation number of f is of periodic type, it is not necessarily the same renormalization sector of ( [7] , Lemma 3.15), because they needed a very specific renormalization sector that comes from the results of McMullen [5] , which projects the prepacman to the same Siegel Pacman.
The definition of the set
is analogous to the definition of the horseshoe
in ( [3] , p.389-390), but instead of the a priori bounds condition ( [3] , p. 367), we ask that the rotation number be in the set
so the elements of the continued fraction are bounded by the constant M.
Definition 11. Let us define the set
as the subset of angles such that the elements of its continued fraction are bounded by the constant M, that is, if
or
then
if and only if
, for all
.
The set of completely non-escaping points
is the set of hybrid classes
of standard Siegel Pacman, with a fixed truncation level, with their rotation number
. To θ we can assign the infinite sequence
which depends on the elements of its continued fraction. Then we can take any sequence
such that
, with which we obtain a bi-infinite sequence
related with θ. So we will have that
is infinitely Pacman renormalizable backwards and forwards, which means that for all
there are hybrid classes
and
defined by their rotation number
(or
depending on if
or
and if n is odd or even) such that
, where
and renormalizing a hybrid class means doing the Pacman renormalization on some representative
in such a way that
acts on the rotation number
as
analogously in the case
the operator
acts as
Note that due to Theorem 5, the Pacman renormalization operator
on
is always well defined. Also this set is not empty because at least there are the classes
such that its rotation number
is periodic with
, and we can associate the bi-infinite sequence:
Remark 3. By the last definition given
, automatically we have a sequence of classes
such that
, which in turn generates a sequence of angles
defined by the rotation number of each class
. Due to the condition
and how
acts on the rotation number, we can get a bi-infinite sequence
whose elements are the natural numbers that define the rotation numbers of the classes
.
The following definitions for the conjugation construction are analogous to ( [3] , p.389-391).
Definition 12. The natural extension
of the map
is defined as the lift of
to the space of two-sided orbits
, where
, then
is a homeomorphism with respect to the weak topology on
. Which means that
converges to
when
if and only if given
the coordinate
is well defined as long as the coordinate
is well defined and when this happens
when
, that is, for each m there is a representavive of
such that they converge to a representative of
in the space of analytic functions with the supreme norm.
We also consider the space
of bi-infinite sequences
of natural numbers bounded by the constant M with the weak topology (i.e. pointwise convergence as above). Let
stand for the left shift in this space, sometimes called the Bernoulli shift, so that a1 is the zero coordinate of
.
The next remark tell us that
is a closed subset of
, it will allow us to define the renormalization horseshoe of the Pacman renormalization operator on the hybrid classes of standard Siegel pacmen. By renormalization horseshoe we mean a set that is invariant under the operator RM, sequentially compact and RM is topologically semi conjugated to the Bernoulli shift operator in the space of symbols
.
Remark 4. Given any
, the set
of irrational numbers
(the case
is analogous) such that
, for all
, is a closed set. Indeed let
, where
and suppose that there is a
such that
when
. Therefore θ is also irrational and since the continued fraction expansion is unique, for all
there are
such that if for all
,
, then
, for all
. So for all
,
. And since for all
,
, then its limit is also bounded by M, that is,
for all
. Thus
.
Now we are ready to prove the main theorem of this article.
Theorem 6. For any
, the set
is a horseshoe for the renormalization operator
which acts on the hybrid classes of standard Siegel pacmen with rotation number in
. The natural extension
is a homeomorphism topologically conjugated to the left shift
while
is semiconjugate to ω.
In summary we are going to prove that the following diagram is commutative and that the functions in it are continuous.
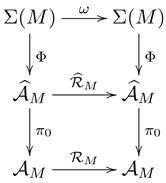
We will divide the proof of the theorem into the following lemmas.
Lemma 7. The set
is precompact with respect to orbit renormalization.
Proof. Let’s see that given
, which by remark 3 has a sequence of classes associated
such that
and
, then we must find a subsequence
and a class
with
, so we need to find representatives of these classes that converges to a representative of
in the space of analytic functions with the uniform norm.
As we already said in Remark 3, for any
we can associate a sequence of angles
defined by the rotation number of each class
, so given any
we can take the sequence
of rotation numbers associated to each
. Now by Remark 4,
is a closed subset of
, then
must have a subsequence
converging to a
. Since every irrational number has a unique expression in continued fraction, the last convergence says that eventually the first elements
of each
must be equal to the first elements
of the continued fraction of
, that is
for
where
if
.
Now to each
we associate the standard Siegel Pacman class
so it has the rotation number
and in the same way to
associate its class
. To prove that
we need to find representatives where there is convergence.
Define the angle
such that if
(analogous if
), then
; and in the same way for each
we associate
which consists of adding one to the first element of the continued fraction of
. So we have that
,
and
.
Now consider the quadratic polynomials
of Siegel type in the main cardioid of
, which have rotation number θ, that is,
, where
is the α-fixed point of
. Let
be the function that to each
assigns the point
in the boundary of the main cardioid (this is because the α-fixed point of
satisfies that
and
). Therefore g is continuous in its domain.
Set
as the Banach space of analytic functions with the uniform norm. Now define the function
, such that
is the polynomial
. Then the map g is continuous because if
, then
.
When we take the composition of functions
we get a continuous function that to each
assigns the polynomial
. Then as
, we have that
.
If we consider the Pacman renormalization operator applied on
with
( [7] , Lemma 3.4), we can get a standard Siegel Pacman, in such a way that it acts as only one iteration of
on the angle
, that is, subtracting one in the first coefficient of the continued fraction thus
. Then by Theorem 5, there is a neighborhood
, where the Pacman renormalization operator
is compact and analytic.
If we consider the standard Siegel Pacman
, by construction, we have a standard Siegel Pacman with rotation number
therefore it is a representative of the class
(Remark 2). In the same way if
is big enough we have that
and if we consider
we will have a standard Siegel Pacman which has rotation number
, so it is a representative of the class
. Therefore as
and given that the Pacman renormalization operator
is continuous in
, we can conclude that
on some neighborhood of
, that is to say, we have found representatives of the classes where convergence occurs.
Finally let’s see that
. By construction we know that its rotation number
belongs to
so
is infinitely forward renormalizable, but it remains to see that it is infinitely renormalizable backwards, for this we can just add any infinite sequence
bounded by M, in such a way that when combined with the sequence generated by
we get a bi-infinite sequence
which we can associate a sequence of hybrid classes of standard Siegel Pacman
where the rotation number of
is given by
if
is even and
if
is odd. So
and therefore
for all
. 
Lemma 8. The operator
in
is conjugated to the left shift operator ω in
while
is semiconjugated to ω.
Proof. We define the conjugation function
such that for each
assigns
in such a way that the rotation number ρ of each standard Siegel Pacman class is given by:
The function Φ is well defined because by Remark 2 each rotation number determines a unique standard Siegel Pacman class.
Let’s prove that Φ is injective. Indeed if we take two distinct sequences
,
with
and
, then there must be at least one
such that
. Thus
, because they have different rotation numbers, so
.
On the other hand Φ is surjective. Set
, assuming
is even (the odd case is analogous), set
and
. Due to
for all
, this implies
, so
for all
and because this happens to every
we have a single sequence of elements
that defines the rotation numbers of
. Therefore is enough to take
so that
.
Let’s see that Φ is continuous. Given a sequence
with
and
such that
when
, we have to prove that if
and
, then
when
, that is, for all
,
. So we set an entry, say
for example, and find representatives of the classes
and
in the space
where the convergence occurs.
Let
be the space of infinite sequences to the right with elements in the natural numbers, bounded by the constant M, and with the weak topology, we are going to see that the function
such that
(1)
is continuous. For each
we take the sequence
, as by hypothesis
when
, then
converges to
when
, thus for each
we have that
. Due to
, then for each
, there is a
such that for all
it is fulfilled that
.
Note that
is not necessarily the same for each n, but what we can assure is that given an
, there is an
such that for all
,
for
.
If we prove that any two continued fraction expansions
where the first n-elements are equal, then they must satisfy that
(2)
where
.
Then, since we already know that
, we can conclude that for all
, there are
big enough such that if
and
, for
, then
Therefore
and so g is continuous.
First let’s see that (2) is true for finite expressions where the first n-elements are equal, that is of the form
which elements are bounded by M. Doing the subtraction of fractions we get
where
,
.
In the same way when we do the substraction
, we get
where
,
.
Proceeding in an analogous way doing all the subtraction of fractions we obtain that
where
,
for
.
By hypothesis it is fulfilled that
for
, so for
we have
also
implies
and the same happens for
. Therefore we can conclude that (2) is true for the finite case.
Now let’s see that the above is still true when we have infinite continued fractions with the first n-elements are equal, so we take two elements of the form
,
. Indeed, for all
it continuous to be true that
Therefore in the n-th substraction we have:
Now with all the above let’s prove that the function Φ is continuous at the entry
. Since to for each
,
, we consider the sequence
with elements
and a point
. Due to
, then
.
Consider the sequence of angles given by
, which is the rotation number of
but adding one to the first element of its continued fraction. Since the function
defined analogously to (1) is also continuous, then
, when
.
Now we proceed in the same way as we proved the compactness of sequences in
with respect to the renormalization orbits. That is, to each
we sent it to
with
that we already saw is continuous, therefore
. Then to each
we assign the polynomial
in
, which we also saw is continuous, thus
. And finally we apply the Pacman renormalization operator
, which by the Theorem 5 is continuous in a small enough neighborhood of
, in such a way that it acts on the rotation number as
, therefore
. This is how we get the representatives
of the classes
, because they have the same rotation number, which converge to
a representative of
. The same can be done for each
, with
, which belongs to
. Therefore Φ is a homeomorphism.
Finally the operator
is semiconjugated to
because the projection on the zero coordinate
is not injective. 
4. Conclusion
With the previous results, we have built a renormalization horseshoe for the Pacman renormalization operator
for Siegel Pacman functions with bounded rotation number. Due to its conjugation with the left shift operator in the space of bi-infinite sequences of natural numbers bounded by a constant (M) we can perfectly know how the rotation number changes each time the Pacman renormalization operator is applied. The above can be used to construct a stable and unstable manifold for this operator and finally arrive at the result that this is a hyperbolic operator, with which we would have a generalization of ( [7] , Theorem 1.1) and a better understanding of the parameters on the boundary of the main molecule of the Mandelbrot set.
Acknowledgements
Carlos Antonio Marin Mendoza [CVU-714167] thanks Consejo Nacional de Ciencia y Tecnología for its support during the writing of this paper.
Nomenclature/Notation
—The closure of set X.
—The interior of set X.
—The boundary of the set X.
—The set difference of X and A.
—The set A is compactly embedded in the set X.
—The unit disk.
—The Mandelbrot set.
—The set of natural numbers.
—The set of integers numbers.
—The set of rational numbers.
—The set of irrational numbers.
—The set of real numbers.
—The set of complex numbers.