1. Introduction
The basic structure of Hopf algebra was first proposed by Hopf to study algebraic topology and the properties of algebraic groups in 1941 [1]. In 1960’s, Milnor, Moore, Chase and Sweedler systematically developed the theory of Hopf algebra and gave the explicit definition, basic properties and common symbols of Hopf algebra [2] [3] [4]. In 1979, Joni and Rota constructed Hopf algebras on polynomials and on puzzles [5]. After that, Hopf algebra has been used to study a lot of objects, such as posets [6], symmetric functions [7] [8], quantum groups [9] [10], Clifford algebras [11] [12] and Lie superalgebras [13] [14].
Graphs are important combinatorial objects, on which there are rich Hopf algebra structures. In 1994, Schmitt studied incidence of Hopf algebras and gave Hopf algebras on many objects, such as Hopf algebras on permutations, matroids and graphs [15]. Schmitt also studied invariants of graphs through the properties of a Hopf algebra on graphs in 1995 [16]. Later, Connes and Kreimer established connections between quantum physics and Hopf algebras on rooted trees and on rooted forests [17] [18].
Permutations are related to graphs closely. In 1995, Malvenuto and Reutenauer first gave a classical Hopf algebra on permutations by shuffle product
[19]. On this basis, Aguiar and Sottile considered the concept of global descents on permutations in 2005 [20]. In 2004, Novelli, Thibon and Thiéry studied Hopf algebras with bases labeled by graphs and hypergraphs, which are graded by the number of edges [21]. In 2010, Forcey, Lauve and Sottile studied Hopf algebras on binary trees [22]. In 2014, Vargas defined the super-shuffle product
and the cut-box coproduct
on permutations by global ascents of permutations [23]. In 2016, Giraudo and Vialette defined the unshuffle coproduct
on permutations [24]. In 2020, Zhao and Li derived a new Hopf algebra on permutations with another shuffle product
from the classical one [25]. In the same year, Guo, Thibon and Yu introduced the Hopf algebra of signed permutations and established its relationship with the Hopf algebras of permutations and weak quasi-symmetric functions [26]. In 2021, Liu and Li proved that the vector space spanned by permutations arising from the super-shuffle product
and the cut-box coproduct
is a Hopf algebra [27]. It is well-known that permutations are elements of symmetric groups, which are widely used in various fields, such as algebraic number theory [28] and substochastic matrices [29] [30] [31] [32].
In 2020, Aval, Bergeron and Machacek gave a Hopf algebra on labeled simple graphs with the conjunction product and the unshuffle coproduct without a proof. Here the Hopf algebra is graded by the number of vertices. They also introduced a mapping, named
in this paper, from permutations to labeled simple graphs and claimed that it is a Hopf homomorphism [33]. In this paper, we will prove these conclusions.
This paper is organized as follows. We review basic concepts of Hopf algebra in Section 2. In Section 3, we define the vector space
spanned by labeled simple graphs and give the definitions of the conjunction product
and the unshuffle coproduct
on the vector space. In Section 4, we prove
is a graded algebra,
is a graded coalgebra and the compatibility between the conjunction product and the unshuffle coproduct. So
is a Hopf algebra from that
is graded connected. In Section 5, we recall a mapping
from permutations to labeled simple graphs and prove it is a Hopf homomorphism. Lastly, we summarize our main conclusions in Section 6.
In this paper, we not only prove the conclusions but also provide a lot of examples to help people to understand the operation rules and the Hopf structure on labled simple graphs. Furthermore, the Hopf homomorphism from permutations to labled simple graphs idicates the closed relations between them.
2. Hopf Algebra
Firstly, we introduce some basic definitions of Hopf algebra. For more details see [2] [3]. Let
be a commutative ring and
be
-modules. Denote
to be the identity mapping of A. The notation
means that A is isomorphic to B as
-modules.
If there are linear mappings m from
to A and
from
to A such that the diagrams in Figure 1 are commutative, then we say that
is an algebra, m is a product and
is a unit.
If there are linear mappings
from A to
and
from A to
such that the diagrams in Figure 2 are commutative, then we say that
is a coalgebra,
is a coproduct and
is a counit.
We call
a bialgebra, if
is an algebra,
is a coalgebra and A satisfies compatibility, i.e.,
and
for any x and y in A.
The bialgebra
is a Hopf algebra, if there is a linear mapping S from A to A satisfies
for any x in A, i.e., the diagram in Figure 3 is commutative. We call S an antipode.
The vector space A is graded if
and A is connected if
.
The algebra
is a graded algebra if A is a graded vector space, m satisfies
for
and
satisfies
. Similarly, the
coalgebra
is a graded coalgebra if
satisfies
and
satisfies
for any
. The bialgebra
is a graded bialgebra when
is a graded algebra and
is a graded coalgebra. In fact, a graded connected bialgebra is always a Hopf algebra ( [34], Proposition 1.4.14.).
![]()
Figure 1. Associative law and unitary property.
![]()
Figure 2. Coassociative law and counitary property.
3. Basic Definitions
3.1. Labeled Simple Graph
A graph can generally be represented as
, where V is the vertex set and E is the edge set. We call a grpah
a labeled simple graph if it does not have cycles and multiple edges, V is a set of positive integers, also denoted by
, and E is the set of all edges of
, also denoted by
. Obviously,
and if
, then
and
since simple graphs do not have cycles and multiple edges. In particular,
is the empty graph when V is empty, denoted by
.
Let
and
. Define the restriction of
on I by
, where
, and we call
a subgraph of
. If
,
and
, then the union graph of
and
is defined by
. For more details, see [35].
Define
and
Example 1. The graph
is a labeled simple graph and can be represented by
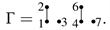
We have
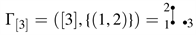
and
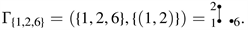
Let
and
be the linear space spanned by
over field
, for any non-negative integer n. For example,

In particular,
and
. Denote
Let
be a set of positive integers where
and denote
, the cardinality of I” at the end of the first sentence. Define a mapping
from I to
by
for
, and call it the standardization of I. For
in I,
if and only if
. Sometimes, we omit the subscript of the standardization when the set is obvious. Let T be a subset of I, then
.
For any labeled simple graph
, define the standard form of
by
where
and
satisfies
for
and
in V. In particular,
. That means, the standardization maintains the edge relationships of the vertices in
. For any labeled simple graph
, there is a graph in
which is the standard form of
, where
. In addition, for a non-negative integer n, let
be the graph by raising each vertex in
by n and maintaining its edge relationships. Similarly, let
be the graph by reducing each vertex in
by n and maintaining its edge relationships.
Example 2. For labeled simple graph
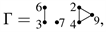
we have
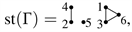
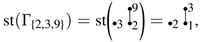
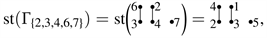
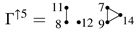
and
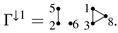
3.2. Conjunction Product and Unshuffle Coproduct
Define the conjunction product
on
[33] by
for
in
and
in
, and the unit
from
to
by
.
Example 3. For 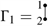 and
and 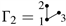 , the conjunction product of
and
is
, the conjunction product of
and
is
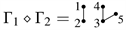
and the conjunction product of
and
is
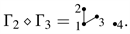
Define the unshuffle coproduct
on
[33] by
for
in
, and the counit
from
to
by
In particular,
.
Example 4. For  and
and ![]() , the unshuffle coproduct of
is
, the unshuffle coproduct of
is
![]()
and the unshuffle coproduct of
is
![]()
4. Main Theorem
Theorem 2. The vector space
with the conjunction product
and the unit
is a graded algebra.
Proof. For any
in
,
in
and
in
, we have
So,
is associative. It is easy to prove that the
is a unit. Then
is an algebra. Obviously, by the definitions of
and
, we have
for
and
. So
is a graded algebra. □
Example 5. For ![]() and
and ![]() , we have
, we have
![]()
Lemma 1. Assume I is a set of positive integers,
and
.Then
forany i in J. □
Proof. Denote
and
, where
. Suppose
and
. Obviously,
and
for any
. Then
for any
. □
Example 6. If
and
, then
,
and
. On the other hand,
,
,
and
. So
,
,
.
Lemma 2. Assume
is a labeled simple graph,
and
.Then
Proof. For convenience, we denote
is
and
is
. Obviously,
We just need to show that their edges are the same. For
in
, there must exist
and
in K such that
and
. Meanwhile, there must exist
and
in J such that
and
, i.e.,
and
. Then
in
. By the definition of
,
is in
. By Lemma 1,
and
, then
. Similarly, we can prove if
then
. So
□
Example 7. Let ![]() ,
and
then
. We have
,
and
then
. We have
![]()
and
![]()
On the other hand,
![]()
Theorem 2. The vector space
with the unshuffle coproduct
and the counit
is a graded coalgebra.
Proof. Obviously, the empty graph
satisfies
For any
in
where
, we have
(1)
Denote
by
, then
(2)
Denote J as a subset in I such that
, then
. By Lemma 2,
and
Since K in (2) traverses all subsets of
, the corresponding J also traverses all subsets of I. Then (2) can be rewritten as
(3)
Then (1) can be rewritten as
(4)
By the arbitrariness of I and J, (4) can be rewritten as
(5)
Similarly, we can get
is also equal to (5). Then
satisfies coassociativity. It is easy to prove that
is a counit. So,
is a coalgebra.
Obviously, by the definition of
and
, we have
and
for
. So
is a graded coalgebra. □
Next we prove the compatibility between the conjunction product and the unshuffle coproduct.
Lemma 3. Assume
,
and
.Then
Proof. Denote
. Since
, there are no edges between
and
in
, i.e.,
. Then,
.
Since
,
and
. By Lemma 2,
and
Since there are no edges between
and
, there are no edges between
and
. So,
.
Since
,
and
, we have
and
. Then
□
Corollary 1. Assume
,
and
.Then
(6)
where
.
Proof. By the definition of
and Lemma 3,
(7)
Obviously, by the definition of
and Lemma 2, we have
Then (7) can be rewritten as (6). □
Theorem 3.
is a bialgebra.
Proof. Obviously, the counit
is an algebra homomorphism. We only need to prove the
is an algebra homomorphism, i.e.,
(8)
for any
and
in H. If
or
then (8) holds. If
and
are non-empty, we denote
and
(9)
Denote
,
,
and
. Furthermore, denote
by
and denote
by
. We have
,
and
. By Corollary 1,
Similarly,
Then (9) can be rewritten as
(10)
Obviously, when I traverses all subsets of
,
and
traverse all disjoint subsets of
,
and
traverse all disjoint subsets of
, and meanwhile
and
travese all disjoint subsets of
.
Then we rewrite (10) as
(11)
By the definition of
, (11) is equal to
Therefore,
So
is a bialgebra. □
Corollary 2.
is a Hopf algebra.
Proof. By Theorem 1, Theorem 2 and Theorem 3,
is a graded connected bialgebra. So it is a Hopf algebra. □
Example 8. For ![]() and
and ![]() , we have
, we have
![]()
![]()
5. Hopf Homomorphism from Permutations to Labeled Simple Graphs
In 2020, Aval, Bergeron and Machacek gave a Hopf homomorphism from permutations to labeled simple graphs without a proof [33]. Next, we prove this mapping is a Hopf homomorphism.
Firstly, we review some basic concepts as follows. For more details, see [27] [33].
Denote
as the set of all permutations of degree n. For any permutation
in
, denote
, where
for
. For example,
. In particular,
, where
is the empty permutation. If
and
, then we define the restriction of
on I by
, and call it a subsequence of
.
More generally, for a set
of positive integers, we call
a sequence on B with length n. Define the standard form of
by
. In fact, any permutation is a sequence. Define
to be the vector space spanned by
over field
. Denote
Next, we review definitions of the conjunction product
and the unshuffle coproduct
on permutations [24] [33].
Define the conjunction product
on
by
and the unshuffle coproduct on
by
for
in
and
in
.
Obviously, we have
for any
and
. Define the unit
by
and the counit
by
for
in S. Then
is a Hopf algebra [33].
Example 9. For
and
, we have
and
For
in
, we call
an inversion of
if
and
. Define a linear mapping
from
to
by
, where
(12)
for
in
. In particular,
. Obviously, each edge of
connects an inversion of
. In fact, we can define the mapping
sending a sequence on B to a labeled simple graph on B by (12).
Example 10. For
and
,
![]()
and
![]()
Next, we prove
is a Hopf homomorphism from
to
, that means it is an algebra homomorphism and a coalgebra homomorphism.
Lemma 4.The mapping
is an algebra homomorphism.
Proof. Suppose
in
and
in
. If
or
is an empty permutation, then obviously
If they are non-empty permutations, then
Since
there are no edges between
and
. If we denote
, then
Denote
and
, then
Obviously,
by the definition of
. On the other hand,
, where
Then
, where
which is equal to
. So
. Then
So
is an algebra homomorphism. □
Lemma 5. Assume
is a non-empty permutation in
and I is a subset of
.Then
Proof. Let
,
and
. Then
and
Denote
for
, then
. If
, then
On the other hand,
, where
If we have
then
And
, where
So
. □
Lemma 6. The mapping
is a coalgebra homomorphism.
Proof. Obviously, for empty permutation
, we have
For any non-empty permutation
, by Lemma 5 we have
So
is a coalgebra homomorphism. □
Corollary 3. The mapping
is a Hopf homomorphism.
Proof. By Lemma 4 and Lemma 6,
is a Hopf homomorphism. □
6. Conclusion
Let
be the vector space spanned by labeled simple graphs. Firstly, we give the definitions of the conjunction product
and the unshuffle coproduct
on
. Then we prove the conjunction product
satisfies associativity and the unshuffle coproduct
satisfies coassociativity, i.e.,
is an algebra and
is a coalgebra. We prove the compatibility between
and
, and
is a graded connected bialgebra. So
is Hopf algebra. Lastly, let
be the vector space spanned by permutations. We recall a mapping
from
to
and prove it is a Hopf homomorphism. In the future, we will study the duality of the Hopf algebra
.
Acknowledgements
This work is supported by National Natural Science Foundation of China (Nos. 11701339 and 12071265).
NOTES
*These authors contributed equally to this work.
#Corresponding author.