1. Introduction
In the 19th century, in order to study differential equations, Lie proposed Lie group theory. Due to the relatively abstract Lie group theory, it was not widely used until the 1970s. It was not until Bluman Cole wrote an intuitive and understandable book [1] in 1974 that Lie group theory became widely used to study and solve nonlinear partial differential equations [2] [3] [4] [5]. The basic idea of Lie group method is to simplify or solve partial differential equations by constructing group invariances as the basis of function transformation.
Gao and Zhang studied a new class of dissipative hyperbolic geometric flows. By applying the Lie group method, the optimal system is obtained, and then the equation is similarly reduced and the exact solution is obtained [6]. They primarily study Lie symmetry analysis and exact solutions for the coupled integrable no dispersion equations, and gave the exact solution in the form of power series [7]. Then, by applying the classical symmetry method, Gao obtained the group invariant solution, the optimal system and the exact solution of the evolution equation of a hyperbolic curve flow [8]. Gao also discussed the normal hyperbolic mean curvature flow with dissipation, and obtained the symmetric optimal system and exact solutions by applying Lie symmetry method [9]. Ding and Wang considered symmetry group and invariant solutions of one dimensional hyperbolic inverse mean curvature flow [10].
In [11], during studying the life-span of classical solutions of hyperbolic inverse mean curvature flow, Wang deduced a hyperbolic equation with Riemann invariance that can be reduced to a hyperbolic Monge-Ampè re equation, namely
(1.1)
In this paper, firstly, we investigate the symmetry group of Equation (1.1). Secondly, we discuss a one-dimensional optimal system of the obtained symmetries. Thirdly, we obtain group-invariant solutions. Finally, we draw conclusions.
2. Symmetry Group
Suppose the one-parameter group of infinitesimal transformations
is given by
(2.1)
in which
is a group parameter.
Let the symmetric group of Equation (1.1) be generated by the vector field in the following form:
(2.2)
The first and second-order prolongation of V are respectively:
The necessary and sufficient condition for Equation (1.1) to remain unchanged under an infinitesimal transformation is that the vector field should satisfy the invariance conditions of Lie symmetry:
(2.3)
in which
, namely
(2.4)
in which
(2.5)
in which
is total differential tox,
are respectively double total differential to x, t,
is the total differential with respect tot and then with respect tox. By substituting (2.5) into Equation (2.4), the decision equations of the original equation can be solved as follows
the above equations can be solved as follows:
(2.6)
in which
are all real constants. Substitute (2.6) into (2.2). Hence the associated seven generators for the one-parameter Lie group of infinitesimal transformations are
(2.7)
The corresponding one-parameter transformation groups are:
3. Optimal System
Definition 3.1: If a set
of r-dimensional subalgebras satisfies the following conditions:
1) Any r-dimensional subalgebras are equivalent to some element in set
;
2) If
, then
is not equivalent to
, then set
is known as ther-dimensional optimal system.
Theorem 3.1: Generators in (2.7) generate an optimal system S:
Proof: By formula
, we get table of Lie brackets (Table 1).
Let’s say any vector
(3.1)
in order to set up the linear transformation of
, let’s say
(3.2)
in which
comes from
. According to (3.2) and table of Lie brackets,
can be written in
for
, Lie equation with parameter
and initial conditions
are as follows

The solution of the above equation consists of the following transformation
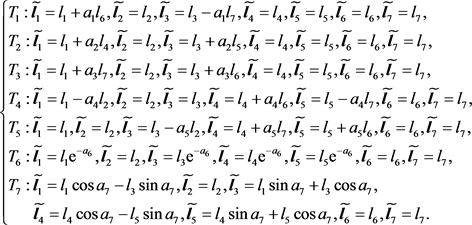
To set up an optimal system, we need to simplify the vector
(3.3)
construct the simplest representation of (3.3) by using transforms
.
Case 1. When
, Let
, make
, so (3.3)
, as a result, we obtain the following representative:
Case 2. When
, Let
,
, make
, so (3.3)
, as a result, we obtain the following representative:
Case 3. When
, Let
, make
, so (3.3)
, as a result, we obtain the following representative:
Case 4. When
, Let
, make
, so (3.3)
.
(4.1) When
, Let
, make
, so (3.3)
; as a result, we obtain the following representative:
.
(4.2) When
, (3.3)
, we obtain the following representative:
Case 5. When
, (3.3)
, Let
, make
, so (3.3)
, as a result, we obtain the following representative:
Case 6. When
, (3.3)
, Let
, make
, so (3.3)
, as a result, we obtain the following representative:
Case 7. When
, (3.3)
, we obtain the following representative:
.
To sum up, optimal system is
4. Group-Invariant Solutions
In this section, using the optimal system, the reduced equations and exact solutions are analyzed for Equation (1.1).
4.1.
The corresponding characteristic equations are
the invariances are
the invariant solutions is
then Equation (1.1) can be reduced as
(4.1)
By solving the above equation, we can get:
When we take
, we have
and
Figure 1 and Figure 2 depict solutions
and
.
4.2.
The corresponding characteristic equations are
the invariances are
the invariant solution is given by
then Equation (1.1) can be reduced as
(4.2)
4.3.
The corresponding characteristic equations are
the invariance is
the invariant solution is given by
then Equation (1.1) can be reduced as
(4.3)
4.4.
The corresponding characteristic equations are
the invariance is
the invariant solution is given by
then Equation (1.1) can be reduced as
(4.4)
4.5.
The corresponding characteristic equations are
the invariance is
the invariant solution is given by
then Equation (1.1) can be reduced as
(4.5)
5. Conclusion
This paper includes four parts: the first part is the introduction, which introduces the background knowledge of the hyperbolic Monge-Ampè re equation and Lie symmetry; in the second part, symmetry group is given; in the third part, optimal system of the symmetry is discussed; in the fourth part, we obtain group-invariant solutions.
Acknowledgements
I would like to thank Z G Wang teacher for drawing my attention to hyperbolic Monge-Ampè re equation. I am grateful to my tutor for her suggestions, which have greatly improved this paper.