Some Integral Inequalities of Simpson Type for Strongly Extended s-Convex Functions

Yixuan Sun, Hongping Yin

College of Mathematics, Inner Mongolia University for Nationalities, Tongliao, China.

DOI: 10.4236/apm.2016.611060                

Abstract

The main purpose of this survey paper is to point out some very recent developments on Simpson’s inequality for strongly extended s-convex function. Firstly, the concept of strongly extended s-convex function is introduced. Next a new identity is also established. Finally, by this identity and H?lder’s inequality, some new Simpson type for the product of strongly extended s-convex function are obtained.

Keywords

Simpson Type Inequality, Integral Identity, Strongly Extended s-Convex Function

1. Introduction

Convex function is a kind of important function and has wide applications in pure and applied mathematics [1] . Since convex analysis appeared in 1960s, there has been tremendous interest in generalizing convex function [2] . In recent years, the generalized convex function and its application have been hot issues. The main purpose of this survey paper is to point out some very recent developments on Simpson’s inequality for strongly extended s-convex function.

First, some definitions concerning various convex functions are listed.

Definition 1.1. A function 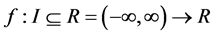is said to be convex if

holds for all 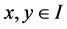and.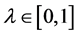

The s-convex function was defined in [3] as follows.

Definition 1.2. A function 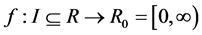is said to be s-convex if

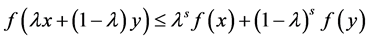(1.1)

for some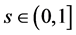, where.

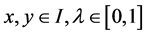If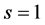, the s-convex function becomes a convex function on.

In [4] , the authors introduced the class of real functions of extended s-convex, defined as follows.

Definition 1.3. ( [4] ). A function is said to be extended s-convex if

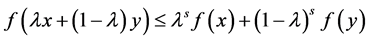(1.2)

for some, where.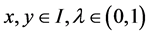

In [5] the concept of strongly convex functions below was innovated.

Definition 1.4. ( [5] ) A function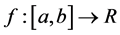 is said to be strongly convex with modulus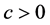, if

(1.3)

is valid for all,.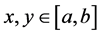

In [6] the concept of strongly s-convex functions was introduced as follows.

Definition 1.5. A function is said to be strongly s-convex with mo- dulus, and some if

(1.4)

is valid all,.

The following inequalities of Hermite-Hadamard type were established for some of the above convex functions.

Theorem 1.1. ( [7] ). Let be differentiable on, with.

(1) If is convex function on, then

. (1.5)

(2) If is convex function on, , then

(1.6)

Theorem 1.2. ( [8] ). Let be differentiable on, with. If is s-convex function on for some fixed and, then

(1.7)

Theorem 1.3. ( [9] ). Let be differentiable on, with, and. If is s-convex function on for some fixed, then

(1.8)

In [6] , Ju Hua et al. established the following theorem.

Theorem 1.4. Let be differentiable mapping on and with. If and is strongly s-convex on for, , then

(1.9)

In this paper, the authors introduce the concept of strongly extended s-convex function and establish a new identity. By this identity and Hölder’s inequality, some new Simpson type for the product of strongly extended s-convex function and discussed and some results are obtained.

2. Definition and Integral Identities

Now the concept of strongly extended s-convex function is introduced.

Definition 2.1. A function is said to be strongly extended s-convex with modulus, if

(2.1)

is valid for all and, some.

For establishing new integral inequalities of Simpson type involving the strongly extended s-convex function, the following identity is needed:

Lemma 2.1. Let be differentiable on and where with. If, then the following identity holds:

(2.2)

Proof. By straightforward computation, the result is followed. The proof is completed.

Lemma 2.2. ( [4] ). Let be differentiable on and with. If, then

(2.3)

3. Some Integral Inequalities of Simpson Type

Theorem 3.1. Let be differentiable mapping on and with. If and is strongly extended s-convex on for, , then

(3.1)

Proof. Using Lemma 2.1 and by Hölder’s inequality, the followings can be obtained:

(3.2)

where,

(3.3)

Again is strongly extended s-convex on, so

(3.4)

(3.5)

(3.6)

Substituting the above (3.3)-(3.6) into the inequality (3.2) results in the inequality (3.1).

Theorem 3.1 is proved.

Corollary 3.2. Under conditions of Theorem 3.1, if, then

Theorem 3.3. Let be differentiable mapping on and with. If and is strongly extended s-convex on for, , then

(3.7)

Proof. Since is strongly extended s-convex on, using Lemma 2.2 and by Hölder’s inequality, the followings can be obtained:

Theorem 3.3 is proved.

Theorem 3.4. Let be differentiable mapping on and with. If and is strongly extended s-convex on for, , then

(3.8)

Proof. By the Lemma 2.1 and using Hölder’s inequality, the followings can be obtained:

(3.9)

where,

(3.10)

Since is strongly extended s-convex on, so

(3.11)

(3.12)

(3.13)

Substituting (3.10)-(3.13) into the inequality (3.9) yields (3.8). Theorem 3.4 is proved.

4. Conclusion

In this paper, the authors introduce the concept of strongly extended s-convex function and establish a new identity. Then by this identity and Hölder’s inequality, some new Simpson type for the product of strongly extended s-convex function are obtained.

Acknowledgements

This work was supported by the National Natural Science Foundation of China No. 11361038 and by the Inner Mongolia Autonomous Region Natural Science Foundation Project under Grant No. 2015MS0123, China.

Conflicts of Interest

The authors declare no conflicts of interest.

References

[1]	Niculescu, C.P. and Persson, L.E. (2005) Convex Functions and Their Applications. CMS Books in Mathematics, Springer-Verlag.
[2]	Dragomir, S.S. and Pearce, C.E.M. (2000) Selected Topics on Hermitr-Hadamard Type Inequalities and Applications, RGMIA Monographs, Victoria University. http://rgmia.org/monographs/hermite_hadamard.html
[3]	Hudzik, H. and Maligranda, L. (1994) Some Remarks on s-Convex Functions. Aequationes Mathematicae, 48, 100-111. http://dx.doi.org/10.1007/BF01837981
[4]	Xi, B.Y. and Qi, F. (2015) Inequalities of Hermite-Hadamard Type for Extended s-Convex Functions and Applications to Means. Journal of Nonlinear and Convex Analysis, 16, 873-890.
[5]	Polyak, B.T. (1966) Existence Theorems and Convergence of Minimizing Sequences in Extremum Problems with Restrictions. Soviet Math.Dokl., 7, 72-75.
[6]	Hua, J., Xi, B.Y. and Qi, F. (2015) Some New Inequalities of Simpson Type for Strongly s-Convex Functions. Afrika Matematika, 26, 741-752. http://dx.doi.org/10.1007/s13370-014-0242-2
[7]	Dragomir, S.S. and Agarwal, R.P. (1998) Two Inequalities for Differentiable Mappings and Applications to Special Means of Real Numbers and to Trapezoidal Formula. Applied Mathematics Letters, 11, 91-95. http://dx.doi.org/10.1016/S0893-9659(98)00086-X
[8]	Kirmaci, U.S. (2004) Inequalities for Differentiable Mappings and Applications to Special Means of Real Numbers to Midpoint Formula. Applied Mathematics and Computation, 147, 137-146. http://dx.doi.org/10.1016/S0096-3003(02)00657-4
[9]	Sarikaya, M.Z., Set, E. and Özdemir, M.E. (2010) On New Inequalities of Simpson’s Type for s-Convex Functions. Computers & Mathematics with Applications, 60, 2191-2199. http://dx.doi.org/10.1016/j.camwa.2010.07.033.