Matrices Associated with Moving Least-Squares Approximation and Corresponding Inequalities

Svetoslav Nenov^*, Tsvetelin Tsvetkov

Department of Mathematics, University of Chemical Technology and Metallurgy, Sofia, Bulgaria.

DOI: 10.4236/apm.2015.514080                

Abstract

In this article, some properties of matrices of moving least-squares approximation have been proven. The used technique is based on known inequalities for singular-values of matrices. Some inequalities for the norm of coefficients-vector of the linear approximation have been proven.

Keywords

Moving Least-Squares Approximation, Singular-Values

Received 17 November 2015; accepted 25 December 2015; published 28 December 2015

1. Statement

Let us remind the definition of the moving least-squares approximation and a basic result.

Let:

1. 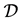be a bounded domain in;

2.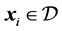,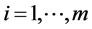;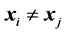, if;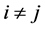

3. 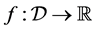be a continuous function;

4. 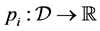be continuous functions,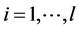. The functions 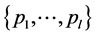are linearly independent in 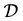and let 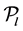be their linear span;

5. 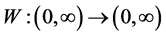be a strong positive function.

Usually, the basis in 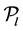is constructed by monomials. For example: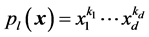, where,

,. In the case, the standard basis is.

Following [1] -[4] , we will use the following definition. The moving least-squares approximation of order l at a fixed point is the value of, where is minimizing the least-squares error

among all.

The approximation is “local” if weight function W is fast decreasing as its argument tends to infinity and interpolation is achieved if. So, we define additional function, such taht:

Some examples of and,:

Here and below: is 2-norm, is 1-norm in; the superscript denotes transpose of real matrix; I is the identity matrix.

We introduce the notations:

Through the article, we assume the following conditions (H1):

(H1.1);

(H1.2);

(H1.3);

(H1.4) w is smooth function.

Theorem 1.1. (see [2] ): Let the conditions (H1) hold true.

Then:

1. The matrix is non-singular;

2. The approximation defined by the moving least-squares method is

(1)

where

(2)

3. If for all, then the approximation is interpolatory.

For the approximation order of moving least-squares approximation (see [2] and [5] ), it is not difficult to receive (for convenience we suppose and standard polynomial basis, see [5] ):

(3)

and moreover (C =const.)

(4)

It follows from (3) and (4) that the error of moving least-squares approximation is upper-bounded from the 2- norm of coefficients of approximation (). That is why the goal in this short note is to discuss a method for majorization in the form

Here the constants M and N depend on singular values of matrix, and numbers m and l (see Section 3). In Section 2, some properties of matrices associated with approximation (symmetry, positive semi-definiteness, and norm majorization by and) are proven.

The main result in Section 3 is formulated in the case of exp-moving least-squares approximation, but it is not hard to receive analogous results in the different cases: Backus-Gilbert wight functions, McLain wight functions, etc.

2. Some Auxiliary Lemmas

Definition 2.1. We will call the matrices

-matrix and -matrix of the approximation, respectively.

Lemma 2.1. Let the conditions (H1) hold true.

Then, the matrices and are symmetric.

Proof. Direct calculation of the corresponding transpose matrices.

Lemma 2.2. Let the conditions (H1) hold true.

Then:

1. All eigenvalues of are 1 and 0 with geometric multiplicity l and, respectively;

2. All eigenvalues of are 0 and −1 with geometric multiplicity l and, respectively.

Proof. Part 1: We will prove that the dimension of the null-space is at least l.

Using the definition of, we receive

Hence,

Using (H1.3), is -matrix with maximal rank l (). Therefore,. More-

over,. That is why or.

Part 2: We will prove that is eigenvalue of with geometric multiplicity, or the system

has linearly independent solutions.

Obviously the systems

(5)

and

(6)

are equivalent. Indeed, if is a solution of (5), then

i.e. is solution of (6).

On the other hand, if is a solution of (6), then

i.e. is solution of (5). Therefore

Part 3: It follows from parts 1 and 2 of the proof that 0 is an eigenvalue of with multiplicity exactly l and is an eigenvalue of with multiplicity exactly.

It remains to prove that 1 is eigenvalue of with multiplicity at least l, but this is analogous to the proven part 1 or it follows dirctly from the definition of.

The following two results are proven in [6] .

Theorem 2.1 (see [6] , Theorem 2.2): Suppose U, V are Hermitian matrices and either U or V is positive semi-definite. Let

denote the eigenvalues of U and V, respectively.

Let:

1. is the number of positive eigenvalues of U;

2. is the nubver of negative eigenvalues of U;

3. is the number of zero eigenvalues of U.

Then:

1. If, then

2. If, then

3. If, then

Corollary 2.1. (see [6] , Corollary 2.4): Suppose U, V are Hermitian positive definite matrices.

Then for any

As a result of Lemma 2.1, Lemma 2.2 and Theorem 2.1, we may prove the following lemma.

Lemma 2.3. Let the conditions (H1) hold true.

1. Then and are symmetric positive semi-definite matrices.

2. The following inequality hods true

Proof. (1) We apply Theorem 2.1, where

Obviously, U is a symmetric positive definite matrix (in fact it is a diagonal matrix). Moreover, , if,.

The matrix V is symmetric (see Lemma 2.1).

From the cited theorem, for any index k we have

In particular, if:

(7)

Let us suppose that there exists index such that

(8)

It fowollws from (8) and positive definiteness of U, that

Therefore (see (7)),. This contradiction (see Lemma 2.2) proves that the matrix is posi- tive semi-definite.

If we set, then by analogical arguments, we see that the matrix is positive semi-definite.

(2) From the first statement of Lemma 2.3, is positive semi-definite. Therefore (see Corollary 2.1 and Lemma 2.2):

for all. Moreover, all numbers, are non-negative and

Therefore

or

□

In the following, we will need some results related to inequalities for singular values. So, we will list some necessary inequalities in the next lemma.

Lemma 2.4. (see [7] [8] ): Let U be an -matrix, V be an -matrix.

Then:

(9)

(10)

(11)

(12)

If and U is Hermitian matrix, then, ,.

Lemma 2.5. Let the conditions (H1) hold true and let,.

Then:

(13)

(14)

(15)

Proof. The matrix is simmetric and positive semi-definite (see Lemma 2.3 (1)). Using the second statement of Lemma 2.3 and Lemma 2.4, we receive

The inequality (14) follows from (12) ().

From (14) and (10), we receive

Therefore, the equality implies the right inequality in (15).

Using and inequality (9), we receive

or, i.e. the left inequality in (15).

The lemma has been proved. □

3. An Inequality for the Norm of Approximation Coefficients

We will use the following hypotheses (H2):

(H2.1) The hypotheses (H1) hold true;

(H2.2),;

(H2.3) The map is -smooth in;

(H2.4),.

Theorem 3.1. Let the following conditions hold true:

1. Hypotheses (H2);

2. Let be a fixed point;

3. The index is choosen such that

Then, there exist constants such that

Proof. Part 1: Let

then

We have (obviously, , and)

Therefore, the function satisfies the differential equation

(16)

Part 2: Obviously

It follows from (15) that

Here, , and. Hence

For the norm of diagonal matrix H, we receive

Therefore, where

We will use Lemma 2.4 to obtain the norm of.

Obviously,. Therefore by (12) (), we have

i.e.

Therefore, if we set, then.

Let the constant be choosen such that

and let.

Part 3: On the end, we have only to apply Lemma 4.1 form [9] to the Equation (16):

Remark 3.1. Let the hypotheses (H2) hold true and let moreover

In such a case, we may replace the differentiation of vector-fuction

by left-multiplication:

The singular values of the matrix are:. Therefore.

That is why, we may chose

Additionally, if we supose, then

Therefore, in such a case:

If we suppose, then obviously, we may set

Conflicts of Interest

The authors declare no conflicts of interest.

References

[1]	Alexa, M., Behr, J., Cohen-Or, D., Fleishman, S., Levin, D. and Silva, C.T. Point-Set Surfaces. http://www.math.tau.ac.il/~levin/
[2]	Levin, D. The Approximation Power of Moving Least-Squares. http://www.math.tau.ac.il/~levin/
[3]	Levin, D. Mesh-Independent Surface Interpolation. http://www.math.tau.ac.il/~levin/
[4]	Levin, D. (1999) Stable Integration Rules with Scattered Integration Points. Journal of Computational and Applied Mathematics, 112, 181-187. http://www.math.tau.ac.il/~levin/ http://dx.doi.org/10.1016/S0377-0427(99)00218-6
[5]	Fasshauer, G. (2003) Multivariate Meshfree Approximation. http://www.math.iit.edu/~fass/603_ch7.pdf
[6]	Lu, L.-Z. and Pearce, C.E.M. (2000) Some New Bounds for Singular Values and Eigenvalues of Matrix Products. Annals of Operations Research, 98, 141-148. http://dx.doi.org/10.1023/A:1019200322441
[7]	Merikoski, J.K. (2004) Ravinder Kumar, Inequalities for Spreads of Matrix Sums and Products. Applied Mathematics E-Notes, 4, 150-159.
[8]	Jabbari, F. (2015) Linear System Theory II. Chapter 3: Eigenvalue, Singular Values, Pseudo-Inverse. The Henry Samueli School of Engineering, University of California, Irvine. http://gram.eng.uci.edu/~fjabbari/me270b/me270b.html
[9]	Hartman, P. (2002) Ordinary Differential Equations. Second Edition, SIAM, Philadelphia, Pennsylvania, United States. http://dx.doi.org/10.1137/1.9780898719222.fm